Dada una función de dos variables que está definida sobre el rectángulo cerrado
$$R=[a,b]\times[c,d]={(x,y)\in\mathbb{R}^{2}\mid a\leq x\leq b,
c\leq y \leq d}$$

suponiendo que $f(x,y)\geq 0$. La gráfica de f es
una superfície con ecuación $z=f(x,y)$. Sea S el sólido que esta
encima de R y debajo de la gráfica de f, es decir
$$S={(x,y,z)\in \mathbb{R}^{3}\mid 0\leq z\leq f(x,y),(x,y)\in R}$$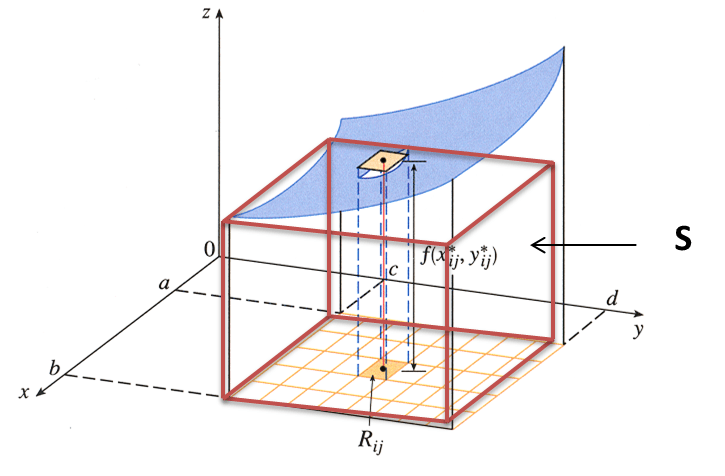

El volumen en esta caso de S es una aproximación al volumen por debajo de la superficie. Ahora bien si dividimos el rectángulo R en subrectángulos. Para el intervalo [a,b] tenemos m subintervalos $[x_{i-1},x_{i}]$ con una longitud de $\displaystyle{\Delta_{x}=\frac{b-a}{m}}$. Para el intervalo [c,d] tenemos n
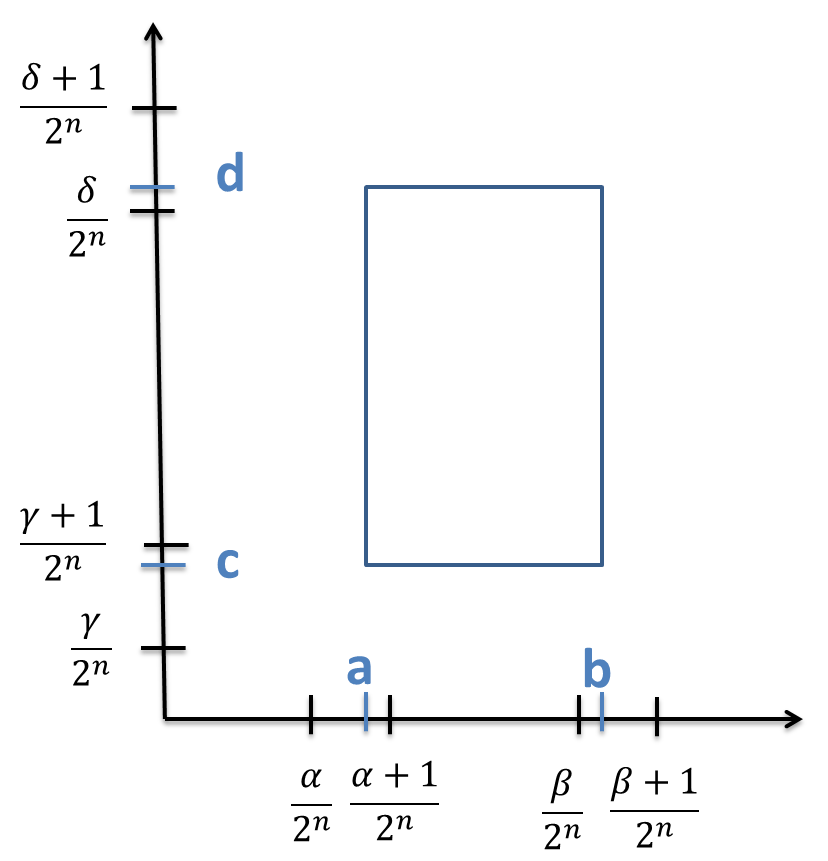
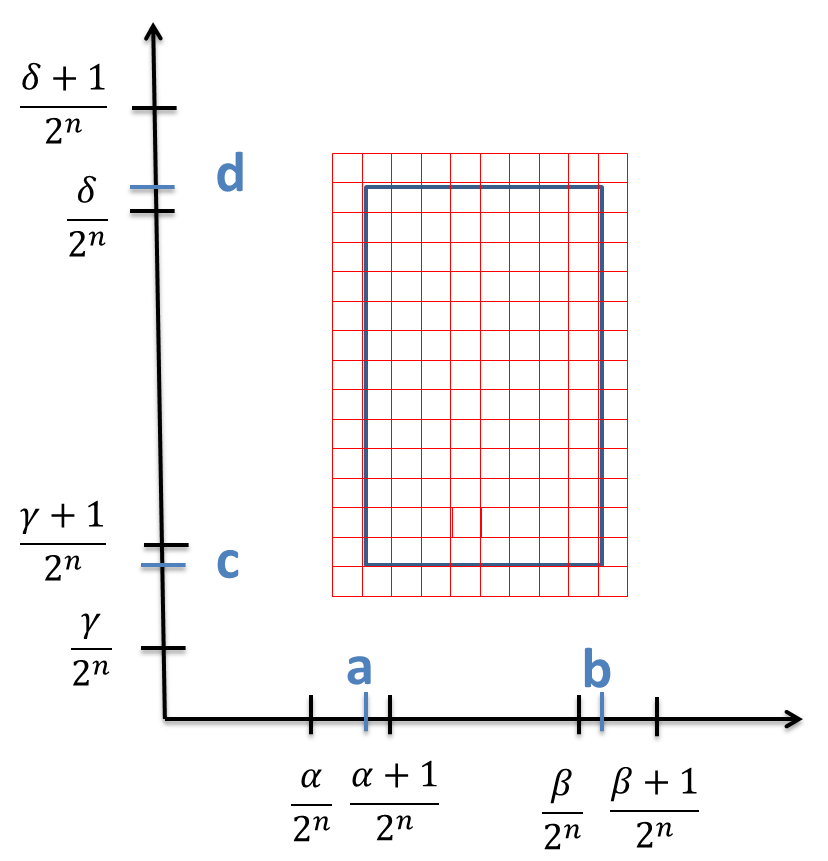
subintervalos $[y_{j-1},y_{j}]$ con una longitud de $\displaystyle{\Delta_{y}=\frac{d-c}{n}}$. Al trazar rectas paralelas a los ejes coordenados a través de los puntos extremos de las particiones formamos los subrectángulos
$$R_{ij}=[x_{i-1},x_{i}]\times[y_{j-1},y_{j}]={(x,y)\in\mathbb{R}^{2}\mid x_{i-1}\leq x\leq
x_{i},y_{j-1}\leq y \leq y_{j}}$$ cada uno con un área igual a $\Delta_{A}=\Delta_{x}\Delta_{y}$. Si elegimos un punto muestra $$(x^{*}_{i},y ^{*} _{j})\in R_{ij}$$, entonces podemos aproximar la parte de S que esta encima de cada $R_{ij}$ mediante una caja rectangular delgada con base $R_{ij}$ y altura $$f( x^{*}_{i},y ^{*} _{j} )$$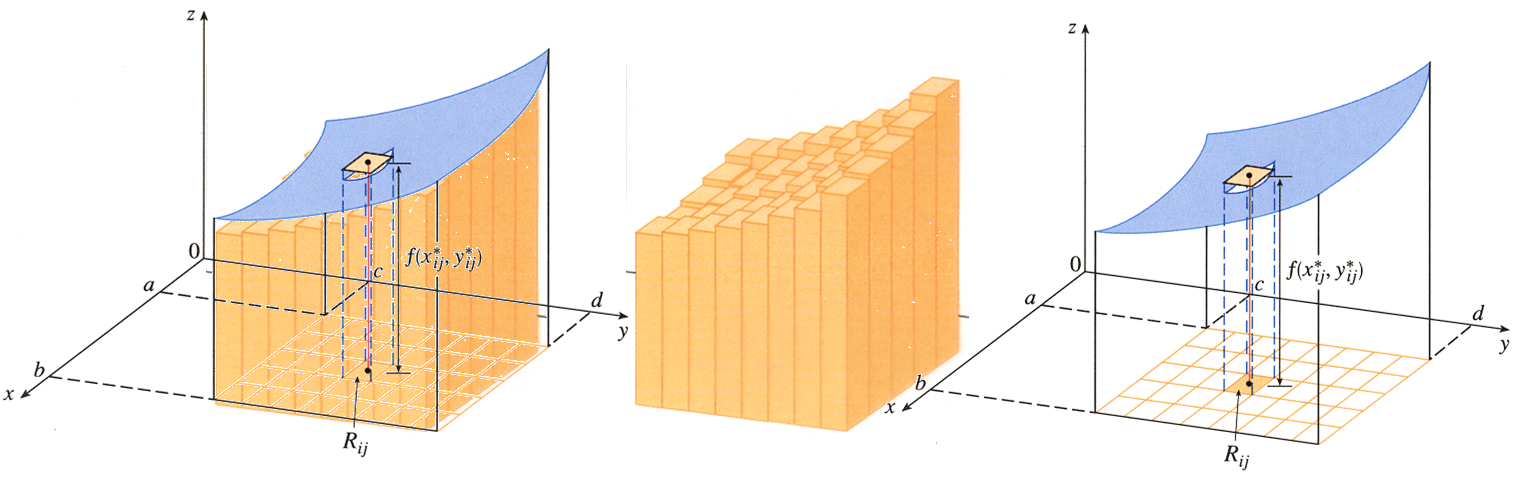

El volumen de la caja es el producto del área de su base por su
altura, por lo tanto una aproximación al volumen de S es:

$$ V\approx\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n} f( x^{*}_{i},y ^{*} _{j}) \Delta_{x}\Delta_{y}$$

Con un desarrollo análogo para un conjunto S el sólido que esta
encima de R y encima de la gráfica de f, es decir
$$S={(x,y,z)\in \mathbb{R}^{3}\mid 0\leq f(x,y)\leq z~|~(x,y)\in R}$$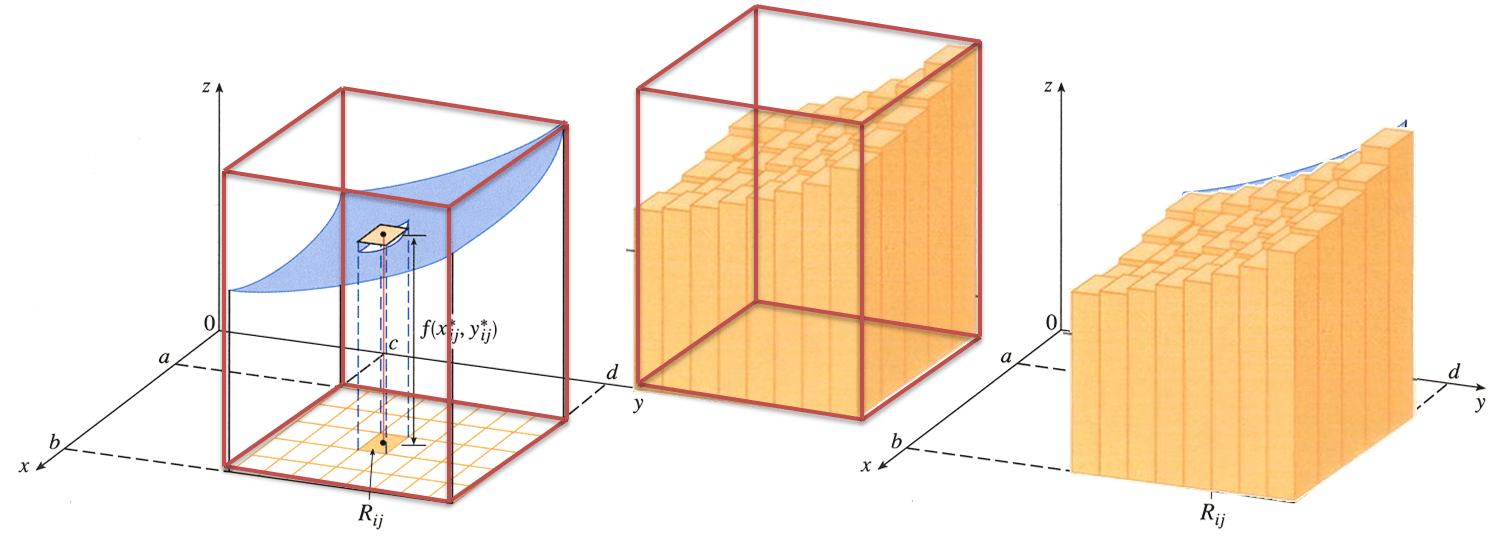

Obtenemos también una aproximación al volumen que se encuentra por debajo de la superficie.
Si consideramos ahora $M_{ij}=sup {f(x_{i},y_{j})}$ y
$m_{ij}=\acute{i}nf{ f(x_{i},y_{j})}$ con $(x_{i},y_{j})\in
R_{ij}$ podemos deducir que
$$\sum_{i=1}^{m}\sum_{j=1}^{n}m_{ij}\Delta R_{ij}\leq V(S)\leq \sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}\Delta R_{ij}$$
Definición.-Sean f una función (de valores reales) definida y
acotada sobre un rectángulo R contenido en $\mathbb{R}^{n}$ y P una
partición de R. Si $R_{1},R_{2},…,R_{k}$ son los subrectángulos de
R inducidos por la partición P, definimos la suma inferior de f
correspondiente a la partición P denotada por $\underline{S}(f,p)$
como $$\underline{S}(f,p)=\sum_{i=1}^{m}\sum_{j=1}^{n}m_{ij}\Delta
R_{ij}$$ Analogamente definimos la suma superior de f
correspondiente a la partición P denotada por $\overline{S}(f,p)$
como
$$\overline{S}(f,p)=\sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}\Delta
R_{ij}$$

Estas sumas tienen una serie de propiedades
Proposición 1: Si P es cualquier partición de R, entonces $$\underline{S}(f,p)\leq\overline{S}(f,p)$$
Demostración: Como $m_{ij}=\acute{i}nf{ f(x_{i},y_{j})}$ y $M_{ij}=sup
{f(x_{i},y_{j})}$ se tiene que $$m_{ij}\leq M_{ij}\Rightarrow
m_{ij}\Delta R_{ij}\leq M_{ij}\Delta
R_{ij}\Rightarrow\sum_{i=1}^{m}\sum_{j=1}^{n}m_{ij}\Delta R_{ij}\leq
\sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}\Delta R_{ij}\Rightarrow
\underline{S}(f,p)\leq \overline{S}(f,p)~\blacksquare$$
Proposición 2: Si $P,Q\in P_{R}$. Si Q refina a P entonces
$$\underline{S}(f,P)\leq\underline{S}(f,Q)\quad y\quad \overline{S}(f,Q)\leq\overline{S}(f,P)$$
Demostración: Sean $R_{1},…,R_{k}$ los subrectángulos inducidos por
P y $R_{1}^{i},…,R_{k}^{i}$ los subrectángulos inducidos por Q.
Dado que cada $R_{j}^{i}$ está contenido en $R_{i}$, tenemos que
${f(\overline{x})\mid \overline{x}\in R_{j}^{i}}\subset
{f(\overline{x})\mid \overline{x}\in R_{i}}$ y por lo tanto
$inf{f(\overline{x})\mid \overline{x}\in R_{i}}\leq
inf{f(\overline{x})\mid \overline{x}\in R_{i}^{j}}$ y
$sup{f(\overline{x})\mid \overline{x}\in R_{j}^{i}}\leq
sup{f(\overline{x})\mid \overline{x}\in R_{i}}$ $\therefore$
$$inf{f(\overline{x})\mid \overline{x}\in R_{i}}\times\Delta R_{ij}\leq
inf{f(\overline{x})\mid \overline{x}\in R_{i}^{j}}\times\Delta
R_{ij}$$
$$sup{f(\overline{x})\mid \overline{x}\in R_{j}^{i}}\times\Delta R_{ij}\leq
sup{f(\overline{x})\mid \overline{x}\in R_{i}}\times\Delta
R_{ij}$$ Si ahora sumamos ambas desigualdades corriendo los índices
i,j se tiene que
$$\sum_{i=1}^{m}\sum_{j=1}^{n}inf{f(\overline{x})\mid \overline{x}\in R_{i}}\leq\sum_{i=1}^{m}\sum_{j=1}^{n}inf{f(\overline{x})\mid \overline{x}\in R_{i}^{j}}$$
$$\sum_{i=1}^{m}\sum_{j=1}^{n}sup{f(\overline{x})\mid \overline{x}\in R_{j}^{i}}\leq\sum_{i=1}^{m}\sum_{j=1}^{n}sup{f(\overline{x})\mid \overline{x}\in R_{i}}$$
Recordando la definición de suma inferior y suma superior se tiene
que$$\underline{S}(f,P)\leq\underline{S}(f,Q)\quad y\quad
\overline{S}(f,Q)\leq\overline{S}(f,P) ~\blacksquare $$
Proposición 3: Si P y Q son cualesquiera dos particiones del
rectángulo R entonces se cumple $$\underline{S}(f,P)\leq
\overline{S}(f,Q)$$
Demostración: Consideremos la partición $P\bigcup Q$. Esta partición
refina tanto a P como a Q de tal forma que, por la proposición 2 se
tiene $$\underline{S}(f,P)\leq\underline{S}(f,P\bigcup Q)$$ y
también
$$\overline{S}(f,P\bigcup Q)\leq\overline{S}(f,Q)$$ Como $$\underline{S}(f,P\bigcup Q)\leq\overline{S}(f,P\bigcup
Q)$$ por la proposición 1, se tiene que
$$\underline{S}(f,P)\leq\overline{S}(f,Q) ~\blacksquare $$
Ejemplo: Estimar el volúmen de la superfície delimitada por el
rectángulo $[0,\pi]\times[0,\pi]$ y la superfície
$f(x,y)=\sin(x+y)$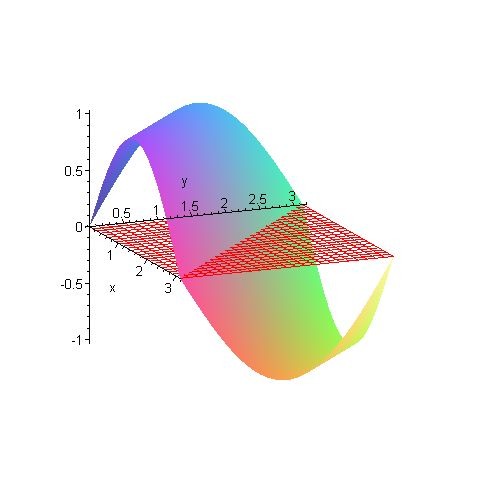

Vamos a subdividir el rectángulo $[0,\pi]\times[0,\pi]$ como se
muestra en la figura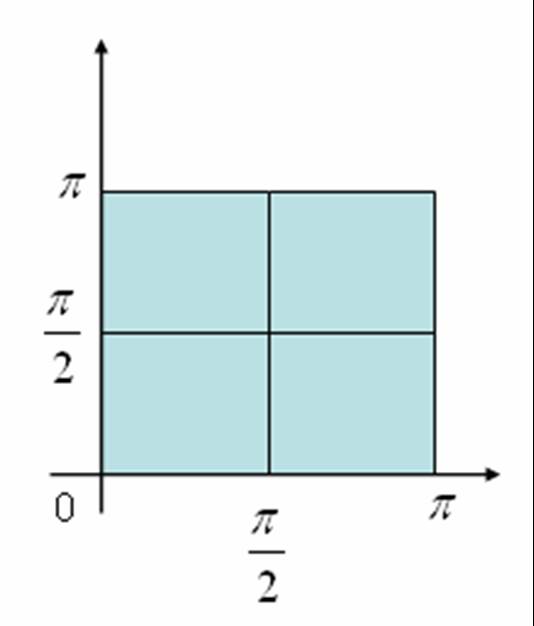

Tenemos por tanto que $$V\approx
\sum_{i=1}^{2}\sum_{j=1}^{2}f(x_{i},y_{j})\triangle
A=f(0,0)\triangle A+f(0,\frac{\pi}{2})\triangle
A+f(\frac{\pi}{2},0)\triangle
A+f(\frac{\pi}{2},\frac{\pi}{2})\triangle A$$
$$=0\times\left(\frac{\pi^{2}}{2}\right)+1\times\left(\frac{\pi^{2}}{2}\right)+1\times\left(\frac{\pi^{2}}{2}\right)+0\times\left(\frac{\pi^{2}}{2}\right)=\frac{\pi^{2}}{2}\approx4.935$$
Definición: Al supremo del conjunto $\underline{S}(f)$ lo
llamamos integral inferior de f sobre R y se puede denotar

$$\underline{\int}R_{f}$$
Y al ínfimo del conjunto $\overline{S}(f)$ lo llamamos integral superior de f sobre R y podemos denotar

$$\overline{\int}R_{f}$$

Definición: Sea
$f:R\subset\mathbb{R}^{n}\rightarrow\mathbb{R}$ acotada sobre el
rectángulo R. Decimos que f es integrable según Riemann sobre R si
se tiene que la integral inferior y la integral superior de f sobre
R son iguales. Es decir

$$\underline{\int}R_{f}=\overline{\int}R_{f}$$

En este caso, a este número lo llamaremos la integral de f y lo denotaremos por
$\displaystyle{\int\int_{R_{f}}}$

Ejemplo: Calcular $\displaystyle{\underline{\int}R_{f}}~~y~~\displaystyle{\overline{\int}R_{f}}$ para $f(x,y)=x+4y$ en el rectángulo $R=[0,2]\times[0,1]$

Solución: Tenemos que para $[0,2]$
consideramos una partición $P={x_{0},x_{1},…,x_{n}}$ con
longitud $\displaystyle{\frac{2-0}{2n}=\frac{1}{n}}$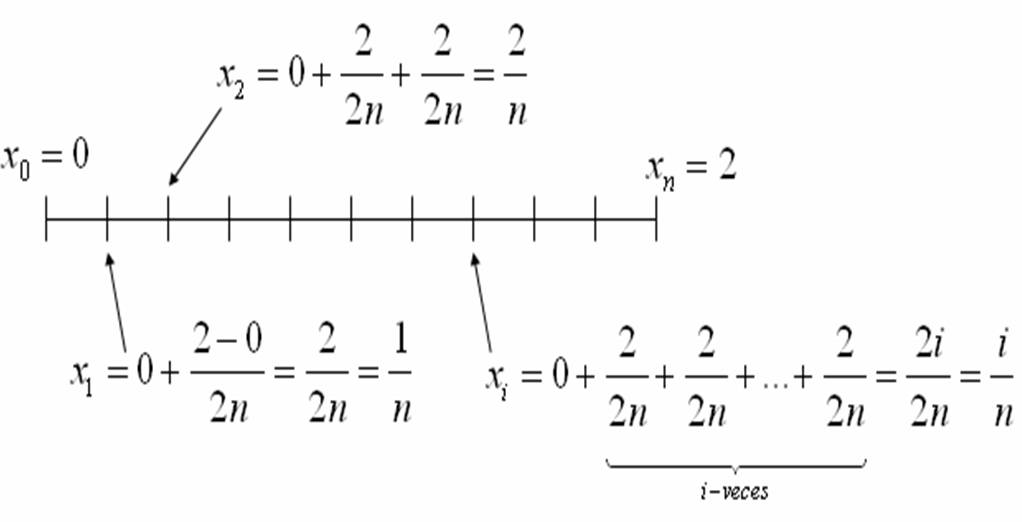

de esta manera se tiene que $\displaystyle{x_{i}=\frac{i}{n}}$ y
$\displaystyle{x_{i-1}=\frac{i-1}{n}}$. Mientras que para $[0,1]$ consideramos una
partición $P={y_{0},y_{1},…,y_{n}}$ con longitud
$\displaystyle{\frac{1-0}{n}=\frac{1}{n}}$ de esta manera se tiene que
$\displaystyle{y_{j}=\frac{j}{n}}$ y $\displaystyle{y_{j-1}=\frac{j-1}{n}}$.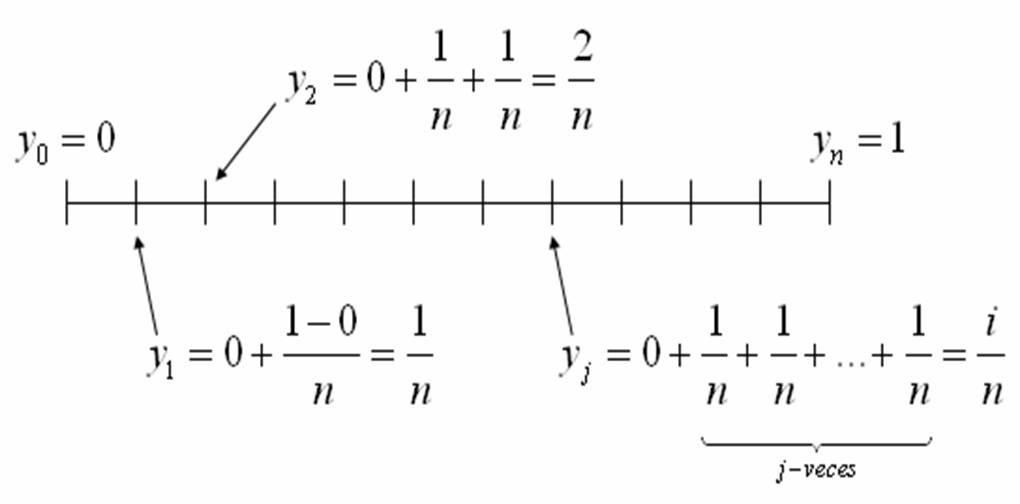

$\therefore$ Para todo rectángulo $R_{ij}$,
$M_{ij}=sup{f(x_{i,j})|x_{ij}\in
[x_{i-1},x:{i}]\times[y_{j-1},y_{j}]}=x_{i}+4y_{j}$ y
$m_{ij}=sup{f(x_{i,j})|x_{ij}\in
[x_{i-1},x:{i}]\times[y_{j-1},y_{j}]}=x_{i-1}+4y_{j-1}$
$\therefore$
$$\underline{S}(f,P)=\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(x_{i-1}+4y_{j-1}\right)\left(\frac{1}{n}\right)\left(\frac{1}{n}\right)=\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(\frac{i-1}{n}+4\frac{j-1}{n}\right)\left(\frac{1}{n}\right)\left(\frac{1}{n}\right)$$
$$=\left(\frac{1}{n^{2}}\right)\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(\frac{i-1}{n}+4\frac{j-1}{n}\right)=\left(\frac{1}{n^{3}}\right)\sum_{i=1}^{2n}\sum_{j=1}^{n}i+4j-5=\left(\frac{1}{n^{3}}\right)\sum_{i=1}^{2n}n(i-5)+4\left(n\left(\frac{n+1}{2}\right)\right)$$
$$=\left(\frac{1}{n^{2}}\right)\sum_{i=1}^{2n}(i-5)+2(n+1)=\left(\frac{1}{n^{2}}\right)\sum_{i=1}^{2n}i+2n-3=\left(\frac{1}{n^{2}}\right)\left(2n(2n-3)+\frac{2n(2n+1)}{2})\right)=$$
$$\left(\frac{1}{n}\right)\left(2(2n-3)+2n+1\right)=\left(\frac{1}{n}\right)(4n-6+2n+1)=\left(\frac{1}{n}\right)(6n-5)=6-\frac{5}{n}$$
$\therefore$
$$\underline{\int}R_{f}=\sup\underline{S}(f,P)=\lim_{n\rightarrow\infty}\underline{S}(f,P)= \lim_{n\rightarrow\infty} 6-\frac{5}{n}=6$$

Ahora bien para $\displaystyle{\overline{S}R_{f}}$

$\therefore$
$$\overline{S}(f,P)=\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(x_{i}+4y_{j}\right)\left(\frac{1}{n}\right)\left(\frac{1}{n}\right)=\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(\frac{i}{n}+4\frac{j}{n}\right)\left(\frac{1}{n}\right)\left(\frac{1}{n}\right)$$
$$=\left(\frac{1}{n^{3}}\right)\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(i+4j\right)=\left(\frac{1}{n^{3}}\right)\sum_{i=1}^{2n}ni+4\left(\frac{n(n+1)}{2}\right)=\left(\frac{1}{n^{3}}\right)\left(n\left(\frac{2n(2n+1)}{2}\right)+2n\left(\frac{4n(n+1)}{2}\right)\right)$$
$$=\left(\frac{1}{ n^{3}}\right)(2n^{3}+n^{2}+4n^{3}+4n^{2})=2+\frac{1}{n}+4+\frac{4}{n}=6+\frac{5}{n}$$

$\therefore$
$$\overline{\int}R_{f}=\sup\overline{S}(f,P)=\lim_{n\rightarrow\infty}\overline{S}(f,P)= \lim_{n\rightarrow\infty} 6+\frac{5}{n}=6$$

Volumen

Cuando definimos volumen aceptaremos el hecho de que si se trata de
un cubo de lado a entonces $V(cubo)=a^{3}$ y si se trata de un
cilíndro circular recto de radio r y altura h entonces
$V(cil\acute{i}ndro)=\pi r^{2}h$

Ejemplo.- Volumen de un cono de altura a.

Para esto, dividamos la altura en n partes iguales, cada una de longitud $\displaystyle{\frac{a}{n}}$. Construyamos los n cilindros de altura $\displaystyle{\frac{a}{n}}$ y radio $r_{k}$, k=1,…,n donde $\displaystyle{r_{k}=k\frac{r}{n}}$.

Entonces el volumen del k-ésimo cilindro es
$$V_{k}=\pi r_{k}^{2}a_{k}=\pi \left(k\frac{r}{n}\right)^{2}\left(\frac{a}{n}\right)=\frac{\pi ar^{2}k^{2}}{n^{3}}$$
Por lo tanto el volumen del cono es
$$V\approx \sum_{k=1}^{n}\frac{\pi ar^{2}k^{2}}{n^{3}}=\frac{\pi
ar^{2}}{n^{3}}\sum_{k=1}^{n}k^{2}=\frac{\pi
ar^{2}k^{2}}{n^{3}}\frac{n(n+1)(2n+1)}{6}=\frac{\pi
ar^{2}}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)
$$
En consecuencia
$$V=\lim_{n\rightarrow \infty}\frac{\pi
ar^{2}}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)=\frac{1}{3}\pi a r^{2}$$

Ejemplo. Volumen de una esfera

Para esto fijémonos en la mitad de la esfera

El radio del k-ésimo cilindro es
$$r_{k}=\sqrt{r^{2}-\left(k\frac{r}{n}\right)^{2}}$$
es decir
$$r_{k}^{2}=r^{2}-\left(k\frac{r}{n}\right)^{2}$$
entonces el volumen del k-ésimo cilindro es
$$V=\pi r_{k}^{2}\frac{r}{n}=\pi
\left(r^{2}-\left(k\frac{r}{n}\right)^{2}\right)\frac{r}{n}=\pi
r^{2}\left(1-\frac{k^{2}}{n^{2}}\right)\frac{r}{n}=\pi
r^{3}\left(1-\frac{k^{2}}{n^{2}}\right)\frac{1}{n}$$
Es la mitad de la esfera, por lo que
$$V\approx 2\sum_{k=1}^{n} \pi
r^{3}\left(1-\frac{k^{2}}{n^{2}}\right)\frac{1}{n}=2 \pi
r^{3}\left(\frac{1}{n}\sum_{k=1}^{n}1-\frac{1}{n^{3}}\sum_{k=1}^{n}k^{2}\right)$$
$$=2 \pi r^{3}\left(1-\frac{1}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)\right)
$$
Por lo tanto
$$V=\lim_{n\rightarrow\infty}2 \pi
r^{3}\left(1-\frac{1}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)\right)=\frac{4}{3}\pi r^{3}$$

Ejemplo.- ¿Cual es el volumen del sólido que esta acotado superiormente por un plano e inferiormente por un cilindro?

Para resolver esto, dividimos en triángulos rectángulos

Tenemos que según la figura
$$\left(\frac{l_{k}}{2}\right)^{2}+\left(\frac{kr}{n}\right)^{2}=r^{2}$$
por lo tanto
$$l_{k}=2\sqrt{r^{2}-\left(k\frac{r}{n}\right)^{2}},~~\overline{PQ}=k\frac{a}{n}$$

se tiene entonces que
$$V_{k}=\left(2\sqrt{r^{2}-\left(k\frac{r}{n}\right)^{2}}\right)\left(\frac{ka}{n}\right)\left(\frac{r}{n}\right)$$
$$V\approx
2r^{2}a\sum_{k=1}^{n}\left(\frac{k}{n}\right)\sqrt{1-\left(\frac{k}{n}\right)^{2}}\left(\frac{1}{n}\right)$$

$$V=2r^{2}a\lim_{n\rightarrow
\infty}\sum_{k=1}^{n}\left(\frac{k}{n}\right)\sqrt{1-\left(\frac{k}{n}\right)^{2}}\left(\frac{1}{n}\right)=2r^{2}a\int_{0}^{1}x\sqrt{1-x^{2}}dx=\frac{2r^{2}a}{3}$$

Definición: Área

La noción intuitiva de área de una región en el plano es el número
de unidades cuadradas contenidas en la región.

Al definir área aceptaremos que el área $A(S)$ de un conjunto
debe ser un número no negativo con las propiedades siguientes:

1.-Si S es un cuadrado de lado K entonces $A(S)=K^2$

2.-El área del todo es la suma de las áreas de sus partes.
Más precisamente si $S$ consiste de los conjuntos que no se
traslapan $S_{1}$,…,$S_{n}$ de áreas $A(S_{1})$,…,$A(S_{n})$
respectivamente, entonces el área de $S$ es $$A(S)=A(S_{1})+\ldots+A(S_{n}).$$

Los cuadrados congruentes proporcionan la manera más fácil de
cubrir el plano sin espacios vacíos o traslapes. Usaremos la rejilla asociada al sistema coordenado proporcionada por
las rectas $x=0,\pm1,\pm2,…$ e $y=0,\pm1,\pm2,…$ la cual
divide al plano en cuadrados de lado 1.

Denotamos $\displaystyle {A_0^{+}(S)}$ el número de cuadrados que
tienen puntos en común con $S$ y $\displaystyle {A_0^{-}(S)}$ el
número de aquellos que están completamente contenidos en $S$

Dividamos ahora cada cuadrado en 4 partes iguales de lado
$\displaystyle{\frac{1}{2}}$ y área $\displaystyle{\frac{1}{4}}$.
Sea $\displaystyle A_1^{+}(S)$ la cuarta parte del número de
aquellos subcuadrados que tienen puntos en común con $S$ y
$\displaystyle A_1^{-}(S)$ la cuarta parte de aquellos completamente
contenidos en $S$.

Se tiene que $\displaystyle{A_0^{-}(S)\leq\displaystyle A_1^{-}(S)}$ y de modo semejante
$\displaystyle{A_0^{+}(S)\geq A_1^{+}(S)}$, al continuar dividiendo cada cuadrado de lado $\displaystyle{\frac{1}{2}}$ en 4 cuadrados de lado $\frac{1}{4}$. Un dieciseisavo de esos cuadrados que tienen puntos en común con $S$ y un dieciseisavo de esos cuadrados que estan completamente contenidos en $S$, se denotaran por
$\displaystyle{A_2^{+}(S)}$ y $\displaystyle{A_2^{-}(S)}$. \Procediendo de esta forma se asocian los valores $\displaystyle{A_n^{+}(S)}$ y $\displaystyle{A_n^{-}(S)}$ con una división en cuadrados de lado $2^{n}$. Es evidente que los valores $\displaystyle{ A_n^{+}(S)}$ forman una sucesión monótona decreciente y acotada que converge hacia un valor $\displaystyle{A^{+}(S)}$, mientras que los valores $\displaystyle{A_n^{-}(S)}$ crecen monótonamente y convergen hacia un valor $\displaystyle{A^{-}(S)}$.
El valor $\displaystyle{A^{-}(S)}$ representa el área interior, lo mejor que
puede aproximarse el área de $S$ desde abajo por medio de cuadrados
congruentes contenidos en $S$, el área exterior $\displaystyle{A^{+}(S)}$
representa la mejor cota superior obtenible cubriendo a $S$ por
medio de cuadrados congruentes. Podemos denotar $\displaystyle{ A_n^{-}=\sum_{ik}
2^{-2n}}$ con $R_{ik}\subset S$, $\displaystyle{A_n^{+}=\sum_{ik}2^{-2n}}$ con $R_{ik}\cap S\neq\emptyset$ a partir de la definición resulta $0\leq\displaystyle {A_n^{-}}\leq\displaystyle{A_n^{+}}$.\ Las sumas $\displaystyle {A_n^{-}}$ forman una sucesión no decreciente con la cota superior $\displaystyle{A_1^{+}}$ así, convergen hacia un limite $A^{-}=\displaystyle{\lim_{n\rightarrow\infty} A_n^{-}}$.
De manera semejante Las sumas $\displaystyle{A_n^{+}}$ forman una sucesión no
creciente con la cota superior $\displaystyle{A_1^{-}}$ así, convergen hacia un limite
$A^{+}=\displaystyle{\lim_{n\rightarrow\infty}} \displaystyle {A_n^{+}}$.
Si ambos valores concuerdan se dice que $S$ es mesurable según
Jordan y el valor común $\displaystyle{A^{-}(S)=A^{+}(S)}$ se llama contenido, o
medida de Jordan de $S$.

Más generalmente, cualquier rectángulo $S$ con lados paralelos a
los ejes coordenados, $S: a\leq x\leq b,~~~c\leq y\leq d$.

Dado un entero positivo n, se pueden encontrar enteros
$\alpha,~\beta,~\gamma,~\delta$ tales que

$\alpha <a\cdot2^{n}\leq\alpha+1,~~~\gamma<c\cdot2^{n}\leq\gamma+1$

$\beta\leq b\cdot2^{n}<\beta+1~~~~\delta\leq d\cdot2^{n}<\delta+1$

por lo tanto
$\displaystyle{\frac{\alpha}{2^{n}}<a\leq\frac{ \alpha+1}{2^{n}}}$
$\displaystyle{\frac{\gamma}{2^{n}}<c\leq\frac{ \gamma+1}{2^{n}}}$

$\displaystyle{\frac{\beta}{2^{n}}\leq b<\frac{\beta+1}{2^{n}}}$

$\displaystyle{\frac{\delta}{2^{n}}\leq d<\frac{\delta+1}{2^{n}}}$

Usando una rejilla adecuada de longitud $2^{n}$ tenemos que

$\displaystyle{\frac{\beta}{2^{n}}-\frac{\alpha+1}{2^{n}}+\frac{2}{2^{n}}\leq b-a+\frac{2}{2^{n}}}$

$ \displaystyle{ \frac{\beta+1}{2^{n}}-\frac{\alpha}{2^{n}}-\frac{2}{2^{n}}\geq b-a-\frac{2}{2^{n}}}$

$ \displaystyle{ \frac{\delta}{2^{n}}-\frac{\gamma+1}{2^{n}}+\frac{2}{2^{n}}\leq d-c+\frac{2}{2^{n}}}$

$ \displaystyle{ \frac{\delta+1}{2^{n}}-\frac{\gamma}{2^{n}}-\frac{2}{2^{n}}\geq d-c-\frac{2}{2^{n}}}$

Por lo tanto
$$A_{n}^{+}=\left(\frac{\beta}{2^{n}}-\frac{\alpha+1}{2^{n}}+\frac{2}{2^{n}}\right)\left(\frac{\delta}{2^{n}}-\frac{\gamma+1}{2^{n}}+\frac{2}{2^{n}}\right)$$
$$A_{n}^{-}=\left(\frac{\beta+1}{2^{n}}-\frac{\alpha}{2^{n}}-\frac{2}{2^{n}}\right)\left(\frac{\delta+1}{2^{n}}-\frac{\gamma}{2^{n}}-\frac{2}{2^{n}}\right)$$

De la desigualdad
$$A_{n}^{-}\leq A\leq A_{n}^{+}$$
tenemos que
$$\left(\frac{\beta+1}{2^{n}}-\frac{\alpha}{2^{n}}-\frac{2}{2^{n}}\right)\left(\frac{\delta+1}{2^{n}}-\frac{\gamma}{2^{n}}-\frac{2}{2^{n}}\right)\leq A\leq\left(\frac{\beta}{2^{n}}-\frac{\alpha+1}{2^{n}}+\frac{2}{2^{n}}\right)\left(\frac{\delta}{2^{n}}-\frac{\gamma+1}{2^{n}}+\frac{2}{2^{n}}\right)$$
como
$$\left(b-a-\frac{2}{2^{n}}\right)\left(d-c-\frac{2}{2^{n}}\right)\leq\left(\frac{\beta+1}{2^{n}}-\frac{\alpha}{2^{n}}-\frac{2}{2^{n}}\right)\left(\frac{\delta+1}{2^{n}}-\frac{\gamma}{2^{n}}-\frac{2}{2^{n}}\right)$$
$$\left(\frac{\beta}{2^{n}}-\frac{\alpha+1}{2^{n}}+\frac{2}{2^{n}}\right)\left(\frac{\delta}{2^{n}}-\frac{\gamma+1}{2^{n}}+\frac{2}{2^{n}}\right)\leq\left(b-a+\frac{2}{2^{n}}\right)\left(d-c+\frac{2}{2^{n}}\right)$$
entonces
$$\left(b-a-\frac{2}{2^{n}}\right)\left(d-c-\frac{2}{2^{n}}\right)\leq A_{n}^{-}\leq A\leq A_{n}^{+}\leq \left(b-a+\frac{2}{2^{n}}\right)\left(d-c+\frac{2}{2^{n}}\right)$$
por lo tanto
$$\lim_{n\rightarrow\infty}\left(b-a-\frac{2}{2^{n}}\right)\left(d-c-\frac{2}{2^{n}}\right)\leq \lim_{n\rightarrow\infty}A_{n}^{-}=A=\lim_{n\rightarrow\infty}A_{n}^{+}\leq \lim_{n\rightarrow\infty}\left(b-a+\frac{2}{2^{n}}\right)\left(d-c+\frac{2}{2^{n}}\right)$$
$A=\displaystyle\lim_{n\rightarrow\infty} \displaystyle
A_n^{+}=\displaystyle \lim_{n\rightarrow\infty} \displaystyle
A_n^{-}=(b-a)(d-c)$.

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Dado un conjunto podemos considerar colecciones formadas por algunos de sus elementos. Estudiaremos estas colecciones que como veremos son también conjuntos y por ende objetos de estudio de la teoría de conjuntos. En esta nota estudiaremos el concepto de subconjunto y a partir de ello estableceremos cuándo dos conjuntos se considerarán iguales. Se desarrollarán pruebas matemáticas intentando explicar a detalle cómo se realizan. Es conveniente que prestes mucha atención a estas demostraciones ya que a lo largo de tus estudios requerirás realizar y entender muchas pruebas y éstas son una parte esencial en las matemáticas.

Definición.

Dados $A$,$B$ conjuntos, decimos que $A$ es un subconjunto de $B$ si todo elemento de $A$ es un elemento de $B$, es decir si para toda $z$, $z\in A$ implica que $z\in B$.

En este caso decimos que $A$ está contenido en $B$ o que $B$ contiene al conjunto $A$.

Nota que $A$ no está contenido en $B$, si existe al menos un $z$, tal que $z\in A$, pero $z\notin B$.

Notación:

Se escribe: $A\subseteq B$ si $A$ está contenido en $B$.

Se escribe: $A\nsubseteq B$ si $A$ no está contenido en $B$.

Si $A$ está contenido en $B$, pero $B$ no está contenido en $A$, decimos que la contención es propia o que $A$ es un subconjunto propio de $B$ y se denota por $A\subsetneq B$ (en este caso si $z\in A$, entonces $z\in B$, pero existe al menos un $z\in B$ tal que $z\notin A$).

Como se mencionó en la nota previa, los números naturales serán conjuntos y resultarán ser distintos como conjuntos cuando sean distintos como números, ver la sección 5.1, página 207, del libro de Avella y Campero que se menciona en la bibliografía de este curso. Para el siguiente ejemplo consideraremos, como usualmente lo hacemos, que los números $1,2,3$ y $4$ son distintos entre sí.

Ejemplo 1

$\set{1,2,3}\subseteq \set{1,2,3}$ ya que los elementos de $\set{1,2,3}$ son $1,2$ y $3$ y cada uno de ellos es un elemento de $\set{1,2,3}$.

$\set{1,2,3}\subseteq \set{1,2,3,4}$ ya que los elementos de $\set{1,2,3}$ son $1,2$ y $3$ y cada uno de ellos es un elemento de $\set{1,2,3,4}$.

$\set{1,2,3, 4}\nsubseteq \set{1,2,3}$ ya que $4\in \set{1,2,3, 4}$ pero $4\notin \set{1,2,3}$ pues $4$ es distinto de $1,2$ y $3$.

$\set{1,2,3}\subsetneq \set{1,2,3,4}$ ya que $\set{1,2,3}\subseteq \set{1,2,3,4}$ pero $\set{1,2,3, 4}\nsubseteq \set{1,2,3}$.

Así, es correcto decir que $\set{1,2,3}$ es un subconjunto de $\set{1,2,3,4}$, pero también que $\set{1,2,3}$ es un subconjunto propio de $\set{1,2,3,4}$, simplemente en el segundo enunciado estamos siendo un poco más precisos.

Proposición

Sean $A$, $B$, $C$ conjuntos.

1. $A\subseteq A$, es decir, cada conjunto se contiene a sí mismo.
2. Si $A\subseteq B$ y $B\subseteq C$, se tiene que $A\subseteq C$. Este hecho se conoce como la propiedad transitiva de la contención de conjuntos.
3. $\emptyset\subseteq A$, es decir, el conjunto vacío es subconjunto de cualquier conjunto.
   

Fíjate muy bien cómo se hace una prueba. Vamos a partir de una afirmación que consideraremos válida, a la que llamaremos hipótesis, y probaremos su consecuencia mediante razonamientos lógicos usando las definiciones o resultados previos.

Demostración de 1
En este primer caso:
La hipótesis es que $A$ es un conjunto cualquiera.
la consecuencia o lo que queremos demostrar es que $A\subseteq A$.
Demostración:
Como queremos probar que un conjunto es subconjunto de otro, entonces tenemos que verificar que la definición de subconjunto se satisface, recuerda que

$A\subseteq B$ si y sólo si para toda $z$, $z\in A$ implica que $z\in B$,

pero en nuestro caso $B=A$. Así, sea $z\in A$, entonces tenemos que $z\in A$. Por lo tanto tenemos que $A\subseteq A$.

$\square$

Demostración de 2

La hipótesis ahora es que $A,B$ y $C$ son conjuntos, con $A\subseteq B$ y $B\subseteq C$
y lo que se tiene que demostrar es que $A\subseteq C$
Demostración:
Dado que queremos probar que $A\subseteq C$, debemos ver que cualquier elemento en $A$ es también un elemento de $C$. Así, consideremos $z\in A$ y verifiquemos que $z\in C$. Como $A\subseteq B$ y $z\in A$, entonces por la definición de subconjunto $z\in B$, y como $B\subseteq C$, nuevamente por la definición de subconjunto $z\in C$. Con ello hemos verificado que para toda $z$, $z\in A$ implica $z\in C$ lo cual es la definición de que $A\subseteq C$, que es exactamente lo que queríamos demostrar.

$\square$

Demostración de 3

De nuevo la hipótesis es que $A$ es un conjunto cualquiera.
lo que queremos demostrar es que el conjunto vacío es un subconjunto de $A$, i.e. $\emptyset\subseteq A$.
Demostración:
Esta prueba la haremos por un método llamado contradicción, el cual consiste en negar la conclusión a la que queremos llegar, manteniendo las mismas hipótesis, y llegar a una contradicción de los teoremas o axiomas de la teoría que se está construyendo.
Primero neguemos la conclusión:

Existe algún conjunto $A$, tal que $\emptyset\nsubseteq A$.

Después se procede a encontrar la contradicción:

Si esto sucediera, es decir si $\emptyset\nsubseteq A$, entonces existiría al menos un elemento en el conjunto $\emptyset$, que no sería elemento del conjunto $A$, pero eso es dar por hecho que el conjunto $\emptyset$ tiene elementos lo cual está en contradicción con el axioma de conjunto vacío visto en la nota anterior.

La contradicción viene de suponer que existe algún conjunto $A$, tal que $\emptyset\nsubseteq A$, por lo tanto no puede existir dicho subconjunto probando así que $\emptyset\subseteq A$ para todo conjunto $A$.

$\square$

Ahora procederemos a dar dos axiomas más, el primero establece cuándo dos conjuntos serán considerados iguales.

Axioma de extensionalidad

Dos conjuntos son iguales cuando tienen exactamente los mismos elementos. Es decir, si $A$ y $B$ son conjuntos:

• $A=B$ significa que $A\subseteq B$ y $B\subseteq A$.
• $A\neq B$ significa que $A\nsubseteq B$ o $B\nsubseteq A$.

Ejemplos

2. Veamos que $\emptyset\neq \{\emptyset\}$.

Notemos que $\emptyset\subseteq \{\emptyset\}$ (ya que por la proposición anterior $\emptyset\subseteq A$ para todo conjunto $A$). Por otro lado recordemos que el conjunto vacío no tiene elementos, así que $A\notin \emptyset$ para todo conjunto $A$, en particular $\emptyset\notin \emptyset$. Tenemos entonces que $\{\emptyset\}\nsubseteq \emptyset$ ya que el único elemento de $\{\emptyset\}$, que es $\emptyset$, no es un elemento del conjunto $\emptyset$.

Así, $\emptyset\subseteq \{\emptyset\}$ pero $\{\emptyset\}\nsubseteq \emptyset$, por lo tanto $\emptyset\neq \{\emptyset\}$. (Intuitivamente podemos imaginar a los conjuntos como cajas y de esa forma $\emptyset$ sería una caja vacía, mientras que $ \{\emptyset\}$ sería una caja que tiene dentro una caja vacía, por lo que tiene sentido considerarlos distintos, ya que la primera caja no tiene nada, mientras que la segunda sí, tiene dentro una caja vacía).

3. Veamos que que $\{\emptyset\}\neq\{\{\emptyset\}\}$.

$\{\emptyset\}\nsubseteq\{\{\emptyset\}\}$ ya que el único elemento de $\{\emptyset\}$, el conjunto $\emptyset$, no es un elemento de $\{\{\emptyset\}\}$, pues el único elemento de $\{\{\emptyset\}\}$ es $\{\emptyset\}$ y como se vio en el ejemplo previo $\emptyset\neq \{\emptyset\}$.

Así, podemos concluir que $\{\emptyset\}\neq\{\{\emptyset\}\}$.

4. Consideremos el conjunto $C$ cuyos elementos son el conjunto vacío, $\emptyset$ y el unitario del vacío, $\{\emptyset\}$, es decir $C=\{\emptyset,\{\emptyset\}\}$. Observamos que:

$\emptyset\in \{\emptyset,\{\emptyset\}\}$ y $\{\emptyset\}\in \{\emptyset,\{\emptyset\}\}$ ya que por construcción $\emptyset$ y $\{\emptyset\}$ son los elementos de $C$.

$\emptyset\subseteq \{\emptyset,\{\emptyset\}\}$ ya que por la proposición previa $\emptyset\subseteq A$ para todo conjunto $A$, en particular $\emptyset\subseteq C$.

$\{\emptyset\}\subseteq \{\emptyset,\{\emptyset\}\}$ ya que el único elemento de $\{\emptyset\}$, que es $\emptyset$, es también un elemento de $\{\emptyset,\{\emptyset\}\}$.

$\{\emptyset,\{\emptyset\}\}\nsubseteq \{\emptyset\}$ ya que existe un elemento en $\{\emptyset,\{\emptyset\}\}$, el elemento $\{\emptyset\}$, que no es un elemento de $\{\emptyset\}$ (ya que el único elemento en $\{\emptyset\}$ es $\emptyset$ y por el ejemplo anterior $\{\emptyset\}\neq \emptyset$).

$\{\{\emptyset\}\}\subseteq \{\emptyset,\{\emptyset\}\}$ ya que el único elemento de $\{\{\emptyset\}\}$, que es $\{\emptyset\}$, es también un elemento de $\{\emptyset,\{\emptyset\}\}$.

Notemos que $\{\{\emptyset\}\}\neq\emptyset$ ya que el único elemento de $\{\{\emptyset\}\}$, que es $\{\emptyset\}$, no es un elemento de $\emptyset$ pues el conjunto vacío no tiene elementos. Por otro lado sabemos por el ejemplo 3 que $\{\{\emptyset\}\}\neq\{\emptyset\}$. Así,

$\{\{\emptyset\}\}\notin \{\emptyset,\{\emptyset\}\}$.

En este último ejemplo notamos que$\{\{\emptyset\}\}\subseteq \{\emptyset,\{\emptyset\}\}$ pero $\{\{\emptyset\}\}\notin \{\emptyset,\{\emptyset\}\}$, haciéndonos ver que las relaciones de pertenencia y de contención no son iguales por lo que debemos ser muy cuidadosos al usar una u otra.

El siguiente nos permite elegir elementos de un conjunto dado que tienen cierta característica en común para formar nuevos conjuntos.

Axioma de separación o de comprensión

Dado $A$ un conjunto y $P$ una propiedad, $\set{\,x\in A\mid\,x\,cumple\,P\,}$ es un conjunto.

Notemos que a diferencia de la colección considerada en la paradoja de Russell dada en la nota anterior, en este caso se considera, no a cualquier objeto con la propiedad $P$, sino a los objetos de algún conjunto que cumplen con la propiedad $P$, es decir partimos de un conjunto y tomamos ahí algunos de sus elementos.

Tarea Moral

1. Considera los conjuntos $B=\{x\in\mathbb{N}\,|\,x \text{ es un número primo}\}$, $C=\{x\in\mathbb{N}\,|\,x \text{ es un número primo y } x>2\}$ y $D=\{x\in\mathbb{N}\,|x\, \text{ es un número impar}\}$.

Determina si las siguientes afirmaciones son verdaderas o falsas:

$i)\,\, B \subseteq D$	$iv)\,\, C \subsetneq B$.
$i)\,\, B \subsetneq D$	$v) \,\, C \subseteq D$.
$iii)\,\, C \subseteq B$.	$vi) \,\, C \subsetneq D$.

2. Considera el conjunto $E=\{\emptyset,\{\{\emptyset\}\}\}$, determina si los siguientes objetos son elementos o subconjuntos de $E$:

$i)\,\, \emptyset\in E$.	$vii)\,\, \{\{\emptyset\}\}\subseteq E$.
$ii)\,\, \emptyset\subseteq E$.	$vii)\,\, \{\{\{\emptyset\}\}\}\in E$.
$iii)\,\, \{\emptyset\}\in E$.	$viii)\,\, \{\{\{\emptyset\}\}\}\subseteq E$.
$iv)\,\, \{\emptyset\}\subseteq E$.	$ix)\,\, \{\{\{\{\emptyset\}\}\}\}\in E$.
$v)\,\, \{\{\emptyset\}\}\in E$.	$x)\,\, \{\{\{\{\emptyset\}\}\}\}\subseteq E$.

3. Intenta hacer las pruebas de las proposiciones tú solo.

Más adelante

En la siguiente nota hablaremos del complemento de un conjunto y deduciremos propiedades básicas pero muy importantes asociadas a este concepto.

Entradas Relacionadas

Página principal del curso.

Nota anterior del curso. Nota 1 Noción de conjunto.

Nota siguiente del curso: Nota 3 El complemento de un conjunto.

Nota. Las imágenes mostradas para ilustrar los conjuntos no fueron de diseño propio, y se da las gracias a: https://www.spanish.cl/ por sus divertidos dibujos. Se deja el link de donde se obtuvieron: https://www.spanish.cl/vocabulario/animales-de-la-granja.htm.

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En esta nota iniciaremos el estudio de los números naturales. Hasta ahora sabemos trabajar con conjuntos, podemos considerar su complemento, unirlos, intersecarlos, considerar subconjuntos de ellos, considerar particiones y relaciones de equivalencia, etc. Con estas herramientas vamos a dar una definición de los números naturales basada en el sucesor, esta definición implicará los llamados axiomas de Peano, en honor al matemático Giuseppe Peano quien en el siglo XIX, los estableció para definir los números naturales. Así nuestro primer objetivo es dar una definición conjuntista de los números naturales y ver que implica los axiomas de Peano. Puedes consultar el siguiente enlace para conocer más a profundidad la historia de cómo se formalizó la aritmética: Los axiomas de Peano.

Empecemos definiendo lo que es el sucesor de un conjunto $x.$

Definición

Sea $x$ un conjunto, el sucesor de $x$ es:

$x^+=x\cup\set{x}.$

Observa que si definimos al cero como el conjunto vacío tenemos que:

$0=\emptyset$

y entonces su sucesor $0^+$ es:

$0^+=\emptyset^+ =\emptyset\cup \set{ \emptyset}= \set{ \emptyset} =\set{ 0}$

Ese sucesor $0^+$ será por definición el $1$, entonces:

$1^+=1\cup\set{1}=\set{0}\cup \set{1}=\set{0,1}$

que es por definición el número 2, y así sucesivamente:

$2^+=2\cup \set{2}= \set{0,1}\cup \set{2}=\set{0,1,2}=3$

$3^+=3\cup \set{3}= \set{0,1,2}\cup \set{3}=\set{0,1,2,3}=4$

$\vdots$

$n^+=n\cup \set{n}= \set{0,\dotsc,n-1}\cup \set{n}=\set{0,\dotsc,n}=n+1$

Aceptaremos que esta construcción puede ser llevada a infinito, y lo postularemos como un axioma.

Axioma del infinito

Existe un conjunto que tiene al cero y al sucesor de cada uno de sus elementos.

Démosle ahora nombre a este tipo especial de conjuntos, aquellos que tienen al cero y todos sus sucesores.

Definición

Sea $A$ un conjunto. Decimos que $A$ es un conjunto de sucesores si tiene como elemento al cero y al sucesor de cada uno de sus elementos.

El la Teoría de Conjuntos a los conjuntos de sucesores también se les llama conjuntos inductivos.

Observemos que el Axioma del infinito asegura la existencia de al menos un conjunto de sucesores. Tiene sentido entonces considerar la intersección de cualquier familia no vacía de conjuntos sucesores y veremos que la intersección también es un conjunto de sucesores.

Lema

Sea $\mathscr F$ una familia no vacía formada por conjuntos de sucesores, entonces $\bigcap\mathscr F$ es un conjunto de sucesores.

Demostración

Sea $\mathscr F$ una familia no vacía formada por conjuntos de sucesores. Como $\mathscr F$ es no vacía, sabemos por la nota nota 14 que podemos considerar el conjunto $\bigcap \mathscr F$ que es la intersección de la colección $\mathscr F$.

Como $A$ es un conjunto de sucesores para todo $A\in \mathscr F$, entonces $0\in A$, para todo $A\in \mathscr F$, así $0\in \bigcap \mathscr F$.

Veamos ahora que $\bigcap \mathscr F$ tiene al sucesor de cada uno de sus elementos.

Sea $x\in \bigcap \mathscr F$ entonces $x\in A$ para todo $A\in \mathscr F$. Como cada $A$ es un conjunto de sucesores, se tiene que $x^+\in A$ para todo $A\in \mathscr F$, así $x^+\in \bigcap \mathscr F$.

Concluimos finalmente que $\bigcap \mathscr F$ es un conjunto de sucesores.

$\square$

Con esta definición de conjunto de sucesores y el lema anterior vamos a definir a los números naturales siguiendo las ideas del libro de José Alfredo Amor mencionado en la bibliografía y las notas de clase de la Dra. Avella. Por el lema anterior, existe un conjunto de sucesores, digamos $T$, por lo que podemos considerar a todos los conjuntos de sucesores contenidos en $T$. La familia $$\{S\subseteq T\,|\,S\text{ es un conjunto de sucesores}\}$$ es no vacía ya que al menos $T$ es uno de sus elementos y, de acuerdo a lo estudiado en la nota 14, podemos considerar su intersección. Así, definiremos a los números naturales como la intersección de esta familia.

Definición

Dado $T$ un conjunto de sucesores fijo sea $\mathscr{F}=\{S\subseteq T\,|\,S\text{ es un conjunto de sucesores}\}$ la colección formada por todos los conjuntos de sucesores contenidos en $T$. El conjunto de los números naturales, denotado por $\mathbb N$ es:

$\mathbb N= \mathop{\displaystyle \bigcap}\mathscr{F}$.

Observación 1

Por el lema anterior, $\mathbb N$ es un conjunto de sucesores, así $0\in \mathbb N$ y si $x\in \mathbb N$, entonces $x^+\in \mathbb N$.

Observación 2

Sea $A$ un conjunto de sucesores cualquiera, entonces, por el lema anterior, $A\cap T$ es un conjunto de sucesores, y como $A\cap T\subseteq T$, entonces $A\cap T$ pertenece a la familia $\mathscr{F}=\{S\subseteq T\,|\,S\text{ es un conjunto de sucesores}\}$. En consecuencia, por las propiedades de la intersección, sabemos que $\mathop{\displaystyle \bigcap}\mathscr{F}\subseteq A\cap T$ y que $A\cap T\subseteq A$. Por lo tanto $\mathop{\displaystyle \bigcap}\mathscr{F}\subseteq A$, es decir, $\mathbb N\subseteq A$.

Esto nos dice que $\mathbb N$ está contenido en cada conjunto de sucesores. Es decir, $\mathbb N$ es el conjunto de sucesores «más pequeño» posible.

Proposición

Si $A\subseteq \mathbb N$ es tal que:

$i)$ $0\in A$, y

$ii)$ para toda $n$, si $n\in A$, entonces $n^+\in A$,

se tiene que $\mathbb N\subseteq A$ y así $A=\mathbb N$.

Demostración

Sea $A\subseteq \mathbb N$ que cumple las condiciones $i$ y $ii$, entonces por definición $A$ es un conjunto de sucesores y de acuerdo a la observación previa sabemos que $\mathbb N$ está contenido en cada conjunto de sucesores, en particular $\mathbb N$ está contenido en $A$, es decir $ \mathbb N\subseteq A$. Así, $A\subseteq \mathbb N$ y $ \mathbb N\subseteq A$ , por lo tanto $A=\mathbb N$.

$\square$

Veremos que la definición que dimos de los números naturales anteriormente implica los axiomas de Peano. Enunciemos dichos axiomas y notemos cómo se derivan de nuestra definición.

Axiomas de Peano

1. $0\in \mathbb N$.

2. Si $n\in \mathbb N$, entonces $n^+\in \mathbb N$.

3. $\forall n\in \mathbb N$, $n^+\neq 0$.

4. $\forall n,m\in \mathbb N$ si $n^+=m^+$, entonces $n=m$.

5. Si $A\subseteq \mathbb N$ es tal que:

$i)$ $0\in A$, y

$ii)$ para todo $n$, si $n\in A$, entonces $n^+\in A$,

se tiene que $\mathbb N\subseteq A$ y así $A=\mathbb N$.

El quinto axioma de Peano se conoce como el Principio de inducción, lo estudiaremos con detalle ya que se usa mucho para hacer pruebas referentes a afirmaciones de los números naturales.

Observa que en nuestro caso los axiomas de Peano no se usarán como axiomas, es decir no partiremos de que se cumplen, pues hemos construido los números naturales a partir de conjuntos, así que se tomarán como una proposición y se demostrará que con esta construcción de los naturales se cumplen las condiciones enunciadas. Sin embargo, les llamaremos axiomas de Peano porque inicialmente se establecieron como axiomas que describían a la colección de los números naturales.

Demostración

Observa que por la observación 1, consecuencia del lema previo que afirma que $\mathbb N$ es un conjunto de sucesores, se tiene que $0\in \mathbb N$, y además si $x\in \mathbb N$, entonces $x^+\in \mathbb N$, por lo que se cumplen los incisos 1 y 2 que se querían demostrar. Por otro lado el inciso $5$ se cumple por la proposición antes demostrada.

Demostración de 3

Queremos demostrar que: $\forall n\in \mathbb N$, $n^+\neq 0$.

Sea $n\in \mathbb N$, por definición $n^+=n\cup\set{n}$. Como $n\in\{n\}$ tenemos que , $n\in n\cup\set{n}$. Así, $n\in n^+$ y entonces $n^+\neq \emptyset=0$.

Para probar $4$ requerimos un resultado.

Lema

Todo elemento de un número natural es también subconjunto de éste.

La prueba de este lema será la primera que realizaremos mediante la técnica de inducción que se basa en el quinto axioma de Peano. La idea esencial es probar que cierta propiedad se cumple para todos los naturales formando un subconjunto $A$ de naturales con todos los naturales que sí cumplen la propiedad, y luego verificando que es igual a $\mathbb N$. Para ello probaremos que

$i)\, 0\in A$ (llamada la base de inducción), y que

$ii)$ si $n\in A$, entonces $n^+\in A$ (llamado paso Inductivo (PI), para ello supondremos que $n\in A$, hipótesis que se conoce comúnmente como la hipótesis de inducción (HI), y probaremos que $n^+\in A$.

Con estas dos condiciones satisfechas podemos asegurar que $A=\mathbb N$ en virtud del quinto Axioma de Peano, y, por lo tanto, que la propiedad se cumple para todo número natural.

En la nota 18 estudiaremos con más detalle este tipo de demostraciones.

Demostración

Esta prueba se hará por inducción usando el quinto axioma de Peano.

Sea $A=\set{n\in \mathbb N\mid si\,\,x\in n \,\, entonces \,\, x\subseteq n}\subseteq \mathbb N$. Probaremos que $A$ cumple $i$ y $ii$ del inciso 5 de la proposición anterior y concluiremos con ello que $A=\mathbb N.$

i) Base de inducción. Primero vamos a probar que el $0\in A$. Como $0=\emptyset$, $0$ no tiene elementos y por vacuidad se cumple entonces que si $x\in 0$, entonces $x\subseteq 0$ (ya que no existen elementos de $0$ y por lo tanto no podríamos exhibir ninguno que no sea subconjunto de $0$). Así, $0\in A$ y se cumple el inciso $i$.

ii) Paso Inductivo. (PI). Ahora, veamos que si $n\in A$, entonces $n^+\in A$.

Sea $n\in A$.

Ésta es nuestra hipótesis de inducción.

Demostración de que $n^+\in A$ usando la HI.

Observa que al estar $n$ en $A$, $n$ cumple la propiedad que caracteriza a los elementos de $A$, es decir, si $x\in n, \,\, entonces \,\, x\subseteq n$. Demostremos con ello que $n^+\in A,$ es decir que todo elemento de $n^+$ es un subconjunto de $n^+$. Consideremos $x\in n^+=n\cup \set{n}$ y verifiquemos que $x\subseteq n^+$.

Caso $1$, $x\in n$

Como $n\in A$ y $x\in n$, entonces $x\subseteq n$, además $n\subseteq n\cup \set{n}= n^+$. Así, $x\subseteq n$ y $n\subseteq n^+$, entonces $x\subseteq n^+$.

Caso $2$, $x\in \set{n}$

En este caso $x=n$ y como $x=n\subseteq n\cup \set{n}=n^+$ tenemos que $x\subseteq n^+.$

En ambos casos, suponiendo que $n\in A$, se tiene que $x\in n^+\,\, implica\,\, que \,\,x\subseteq n^+,$ probando así que $n^+$ es un elemento de $A$.

El conjunto $A$ cumple entonces las condiciones del quinto axioma de Peano (que ya hemos demostrado), y por lo tanto $A=\mathbb N$.

$\square$

Demostración de 4

Sea $n,m\in \mathbb N$ tales que $n^+=m^+$, entonces $n\cup \set{n}= m\cup \set{m}$. Así, $n\in n\cup \set{n}= m\cup \set{m}$, lo que implica que $n\in m$ o $n=m$. Por otro lado $m\in m\cup \set{m}= n\cup \set{n}$, entonces $m\in n$ o $m=n$.

Supongamos por reducción al absurdo que $n\neq m$, entonces se concluye de lo anterior que $n\in m$ y $m\in n$. Por el lema previo $n\subseteq m$ y $m\subseteq n$, así $n=m$, lo cual es una contradicción y por lo tanto $n=m$.

Hemos verificado que la construcción que dimos de los números naturales cumple los axiomas de Peano.

$\square$

Para concluir esta nota, mencionaremos las definiciones y propiedades de la suma y el producto de los números naturales que acabamos de definir. Aunque se presentan las definiciones y se enuncian las propiedades, cabe destacar que las pruebas de las mismas, realizadas por inducción, se desarrollarán en la nota 18b con el fin de estudiar primero la inducción matemática en casos menos abstractos.

Definición. Suma en $\mathbb N$

Dado $n\in \mathbb N$ definimos:

$n+0=n,$

para todo $m\in \mathbb N$, $n+m^+=(n+m)^+.$

Propiedades de la suma

Sean $n,m,l\in \mathbb N.$

1. $n+0=n$. Neutro aditivo.
2. $(n+m)+l=n+(m+l)$. Asociatividad.
3. Si $n+l=m+l$, entonces $n=m$. Cancelación.
4. $n+m=m+n$. Conmutatividad.
5. Si $n\neq 0$ o $m\neq 0$, entonces $n+m\neq 0$

Observación 3

Hay que observar que una vez se tiene definida la suma en $\mathbb N$ se puede ver que $n^+=n+1$, donde $1$ es el sucesor de $0$.

Demostración

Sea $m=0$, por definición de la suma en $\mathbb N$ se tiene que $n+0^+=(n+0)^+$. Pero $0^+=1$ y por la definición de suma se tiene que $n+0=n$, por lo que sustituyendo tenemos que $n+1=n^+$.

Definición. Producto en $\mathbb N$

Dado $n\in \mathbb N$ definimos:

$n\cdot 0=0,$

para todo $m\in\mathbb N$, $n\cdot m^+=n \cdot m+n.$

Propiedades del producto

Sean $n,m,l\in \mathbb N.$

1. $1\cdot n=n$. Neutro multiplicativo.
2. $(n+m)\cdot l=n\cdot l+m\cdot l$. Distributividad.
3. $n\cdot m=m\cdot n$. Conmutatividad.
4. $(n\cdot m)\cdot l=n\cdot (m\cdot l)$. Asociatividad.
5. Si $n\neq 0$ y $m\neq 0$, entonces $n\cdot m\neq 0$
6. Si $l\neq 0$ y $n\cdot l=m\cdot l$ entonces $n=m$. Cancelación.

Tarea Moral

1. Describe a los números naturales $3$, $5$ y $7$ como conjuntos, usando la definición conjuntista.

2. Determina si las siguientes afirmaciones se cumplen o no.

• $3\subseteq 5$
• $7\subseteq 5$
• $3\in 5$
• $7\in 3$

3. Prueba que si $n\in \mathbb N$, entonces $n=0$ o $n=m^+$ con $m\in \mathbb N$. Sugerencia: define $A=\{0\}\cup\{m^+|m\in\mathbb{N}\}$ y usa el principio de inducción para demostrar que $A=\mathbb{N}$.

Más adelante

En la siguiente nota definiremos el orden en los números naturales y veremos distintos ejemplos donde aplicaremos el principio de inducción matemática para hacer demostraciones.

Enlaces relacionados

Página principal del curso.

Nota anterior. Nota 15. Relaciones de equivalencia y particiones.

Nota siguiente. Nota 17. El orden en los números naturales.