Dada una función de dos variables que está definida sobre el rectángulo cerrado
$$R=[a,b]\times[c,d]={(x,y)\in\mathbb{R}^{2}\mid a\leq x\leq b,
c\leq y \leq d}$$

suponiendo que $f(x,y)\geq 0$. La gráfica de f es
una superfície con ecuación $z=f(x,y)$. Sea S el sólido que esta
encima de R y debajo de la gráfica de f, es decir
$$S={(x,y,z)\in \mathbb{R}^{3}\mid 0\leq z\leq f(x,y),(x,y)\in R}$$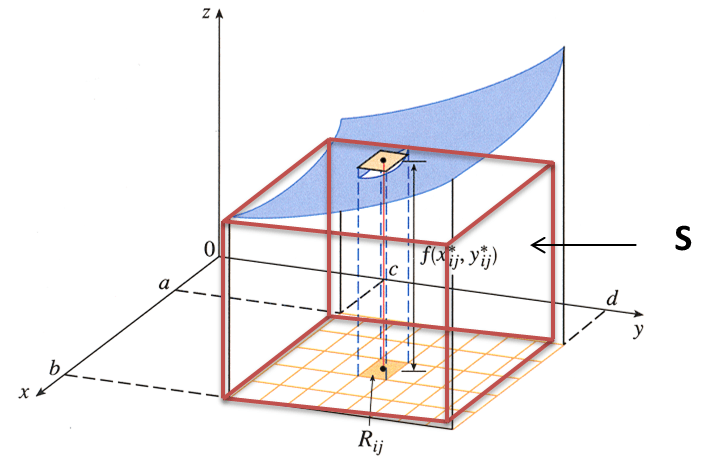

El volumen en esta caso de S es una aproximación al volumen por debajo de la superficie. Ahora bien si dividimos el rectángulo R en subrectángulos. Para el intervalo [a,b] tenemos m subintervalos $[x_{i-1},x_{i}]$ con una longitud de $\displaystyle{\Delta_{x}=\frac{b-a}{m}}$. Para el intervalo [c,d] tenemos n
subintervalos $[y_{j-1},y_{j}]$ con una longitud de $\displaystyle{\Delta_{y}=\frac{d-c}{n}}$. Al trazar rectas paralelas a los ejes coordenados a través de los puntos extremos de las particiones formamos los subrectángulos
$$R_{ij}=[x_{i-1},x_{i}]\times[y_{j-1},y_{j}]={(x,y)\in\mathbb{R}^{2}\mid x_{i-1}\leq x\leq
x_{i},y_{j-1}\leq y \leq y_{j}}$$ cada uno con un área igual a $\Delta_{A}=\Delta_{x}\Delta_{y}$. Si elegimos un punto muestra $$(x^{*}_{i},y ^{*} _{j})\in R_{ij}$$, entonces podemos aproximar la parte de S que esta encima de cada $R_{ij}$ mediante una caja rectangular delgada con base $R_{ij}$ y altura $$f( x^{*}_{i},y ^{*} _{j} )$$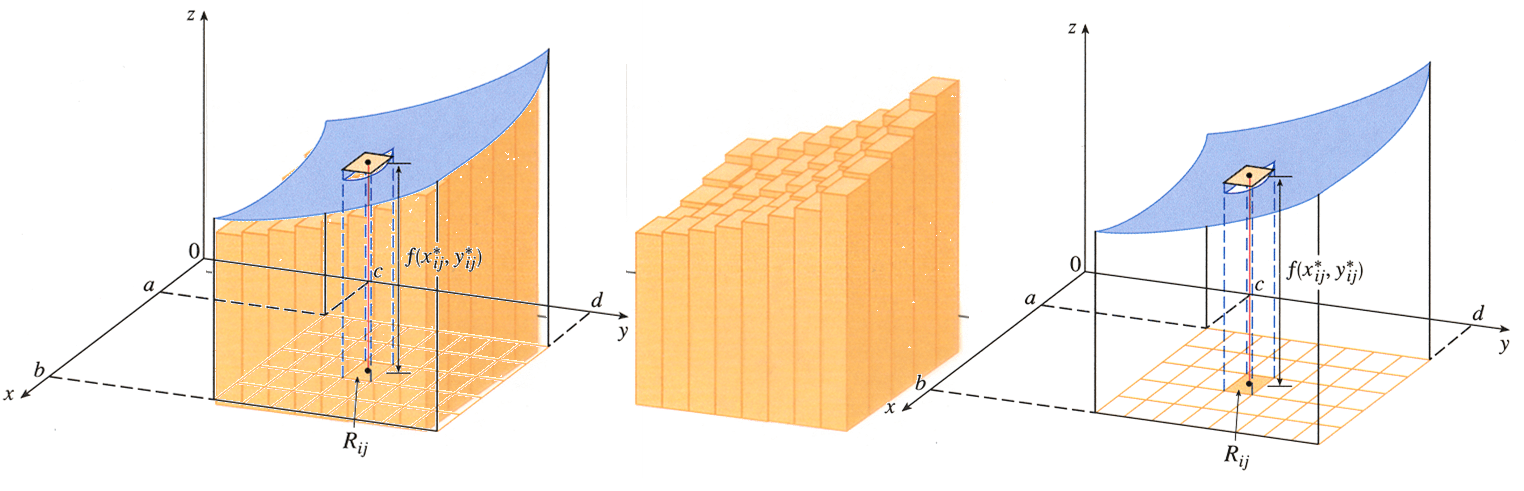

El volumen de la caja es el producto del área de su base por su
altura, por lo tanto una aproximación al volumen de S es:

$$ V\approx\sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n} f( x^{*}_{i},y ^{*} _{j}) \Delta_{x}\Delta_{y}$$

Con un desarrollo análogo para un conjunto S el sólido que esta
encima de R y encima de la gráfica de f, es decir
$$S={(x,y,z)\in \mathbb{R}^{3}\mid 0\leq f(x,y)\leq z~|~(x,y)\in R}$$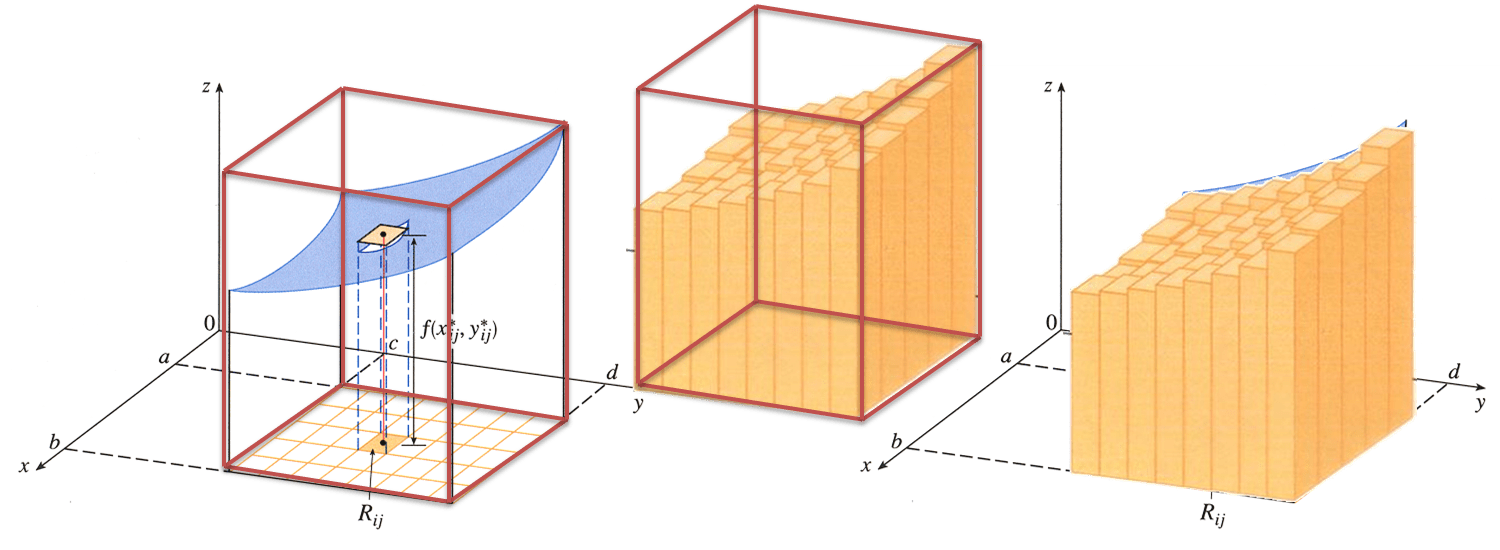

Obtenemos también una aproximación al volumen que se encuentra por debajo de la superficie.
Si consideramos ahora $M_{ij}=sup {f(x_{i},y_{j})}$ y
$m_{ij}=\acute{i}nf{ f(x_{i},y_{j})}$ con $(x_{i},y_{j})\in
R_{ij}$ podemos deducir que
$$\sum_{i=1}^{m}\sum_{j=1}^{n}m_{ij}\Delta R_{ij}\leq V(S)\leq \sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}\Delta R_{ij}$$
Definición.-Sean f una función (de valores reales) definida y
acotada sobre un rectángulo R contenido en $\mathbb{R}^{n}$ y P una
partición de R. Si $R_{1},R_{2},…,R_{k}$ son los subrectángulos de
R inducidos por la partición P, definimos la suma inferior de f
correspondiente a la partición P denotada por $\underline{S}(f,p)$
como $$\underline{S}(f,p)=\sum_{i=1}^{m}\sum_{j=1}^{n}m_{ij}\Delta
R_{ij}$$ Analogamente definimos la suma superior de f
correspondiente a la partición P denotada por $\overline{S}(f,p)$
como
$$\overline{S}(f,p)=\sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}\Delta
R_{ij}$$

Estas sumas tienen una serie de propiedades
Proposición 1: Si P es cualquier partición de R, entonces $$\underline{S}(f,p)\leq\overline{S}(f,p)$$
Demostración: Como $m_{ij}=\acute{i}nf{ f(x_{i},y_{j})}$ y $M_{ij}=sup
{f(x_{i},y_{j})}$ se tiene que $$m_{ij}\leq M_{ij}\Rightarrow
m_{ij}\Delta R_{ij}\leq M_{ij}\Delta
R_{ij}\Rightarrow\sum_{i=1}^{m}\sum_{j=1}^{n}m_{ij}\Delta R_{ij}\leq
\sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}\Delta R_{ij}\Rightarrow
\underline{S}(f,p)\leq \overline{S}(f,p)~\blacksquare$$
Proposición 2: Si $P,Q\in P_{R}$. Si Q refina a P entonces
$$\underline{S}(f,P)\leq\underline{S}(f,Q)\quad y\quad \overline{S}(f,Q)\leq\overline{S}(f,P)$$
Demostración: Sean $R_{1},…,R_{k}$ los subrectángulos inducidos por
P y $R_{1}^{i},…,R_{k}^{i}$ los subrectángulos inducidos por Q.
Dado que cada $R_{j}^{i}$ está contenido en $R_{i}$, tenemos que
${f(\overline{x})\mid \overline{x}\in R_{j}^{i}}\subset
{f(\overline{x})\mid \overline{x}\in R_{i}}$ y por lo tanto
$inf{f(\overline{x})\mid \overline{x}\in R_{i}}\leq
inf{f(\overline{x})\mid \overline{x}\in R_{i}^{j}}$ y
$sup{f(\overline{x})\mid \overline{x}\in R_{j}^{i}}\leq
sup{f(\overline{x})\mid \overline{x}\in R_{i}}$ $\therefore$
$$inf{f(\overline{x})\mid \overline{x}\in R_{i}}\times\Delta R_{ij}\leq
inf{f(\overline{x})\mid \overline{x}\in R_{i}^{j}}\times\Delta
R_{ij}$$
$$sup{f(\overline{x})\mid \overline{x}\in R_{j}^{i}}\times\Delta R_{ij}\leq
sup{f(\overline{x})\mid \overline{x}\in R_{i}}\times\Delta
R_{ij}$$ Si ahora sumamos ambas desigualdades corriendo los índices
i,j se tiene que
$$\sum_{i=1}^{m}\sum_{j=1}^{n}inf{f(\overline{x})\mid \overline{x}\in R_{i}}\leq\sum_{i=1}^{m}\sum_{j=1}^{n}inf{f(\overline{x})\mid \overline{x}\in R_{i}^{j}}$$
$$\sum_{i=1}^{m}\sum_{j=1}^{n}sup{f(\overline{x})\mid \overline{x}\in R_{j}^{i}}\leq\sum_{i=1}^{m}\sum_{j=1}^{n}sup{f(\overline{x})\mid \overline{x}\in R_{i}}$$
Recordando la definición de suma inferior y suma superior se tiene
que$$\underline{S}(f,P)\leq\underline{S}(f,Q)\quad y\quad
\overline{S}(f,Q)\leq\overline{S}(f,P) ~\blacksquare $$
Proposición 3: Si P y Q son cualesquiera dos particiones del
rectángulo R entonces se cumple $$\underline{S}(f,P)\leq
\overline{S}(f,Q)$$
Demostración: Consideremos la partición $P\bigcup Q$. Esta partición
refina tanto a P como a Q de tal forma que, por la proposición 2 se
tiene $$\underline{S}(f,P)\leq\underline{S}(f,P\bigcup Q)$$ y
también
$$\overline{S}(f,P\bigcup Q)\leq\overline{S}(f,Q)$$ Como $$\underline{S}(f,P\bigcup Q)\leq\overline{S}(f,P\bigcup
Q)$$ por la proposición 1, se tiene que
$$\underline{S}(f,P)\leq\overline{S}(f,Q) ~\blacksquare $$
Ejemplo: Estimar el volúmen de la superfície delimitada por el
rectángulo $[0,\pi]\times[0,\pi]$ y la superfície
$f(x,y)=\sin(x+y)$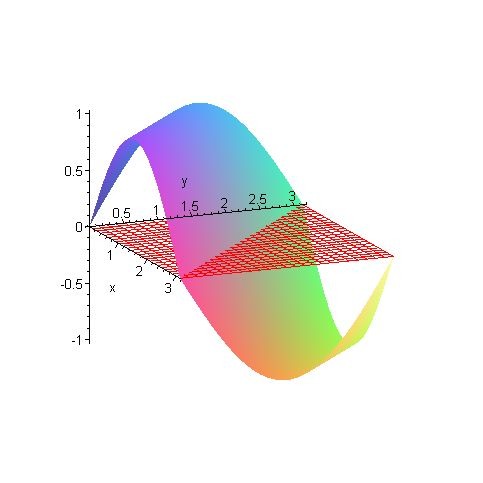

Vamos a subdividir el rectángulo $[0,\pi]\times[0,\pi]$ como se
muestra en la figura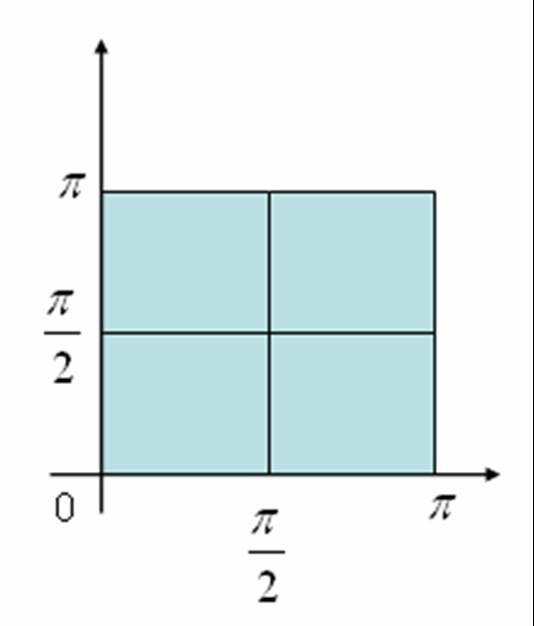

Tenemos por tanto que $$V\approx
\sum_{i=1}^{2}\sum_{j=1}^{2}f(x_{i},y_{j})\triangle
A=f(0,0)\triangle A+f(0,\frac{\pi}{2})\triangle
A+f(\frac{\pi}{2},0)\triangle
A+f(\frac{\pi}{2},\frac{\pi}{2})\triangle A$$
$$=0\times\left(\frac{\pi^{2}}{2}\right)+1\times\left(\frac{\pi^{2}}{2}\right)+1\times\left(\frac{\pi^{2}}{2}\right)+0\times\left(\frac{\pi^{2}}{2}\right)=\frac{\pi^{2}}{2}\approx4.935$$
Definición: Al supremo del conjunto $\underline{S}(f)$ lo
llamamos integral inferior de f sobre R y se puede denotar

$$\underline{\int}R_{f}$$
Y al ínfimo del conjunto $\overline{S}(f)$ lo llamamos integral superior de f sobre R y podemos denotar

$$\overline{\int}R_{f}$$

Definición: Sea
$f:R\subset\mathbb{R}^{n}\rightarrow\mathbb{R}$ acotada sobre el
rectángulo R. Decimos que f es integrable según Riemann sobre R si
se tiene que la integral inferior y la integral superior de f sobre
R son iguales. Es decir

$$\underline{\int}R_{f}=\overline{\int}R_{f}$$

En este caso, a este número lo llamaremos la integral de f y lo denotaremos por
$\displaystyle{\int\int_{R_{f}}}$

Ejemplo: Calcular $\displaystyle{\underline{\int}R_{f}}~~y~~\displaystyle{\overline{\int}R_{f}}$ para $f(x,y)=x+4y$ en el rectángulo $R=[0,2]\times[0,1]$

Solución: Tenemos que para $[0,2]$
consideramos una partición $P={x_{0},x_{1},…,x_{n}}$ con
longitud $\displaystyle{\frac{2-0}{2n}=\frac{1}{n}}$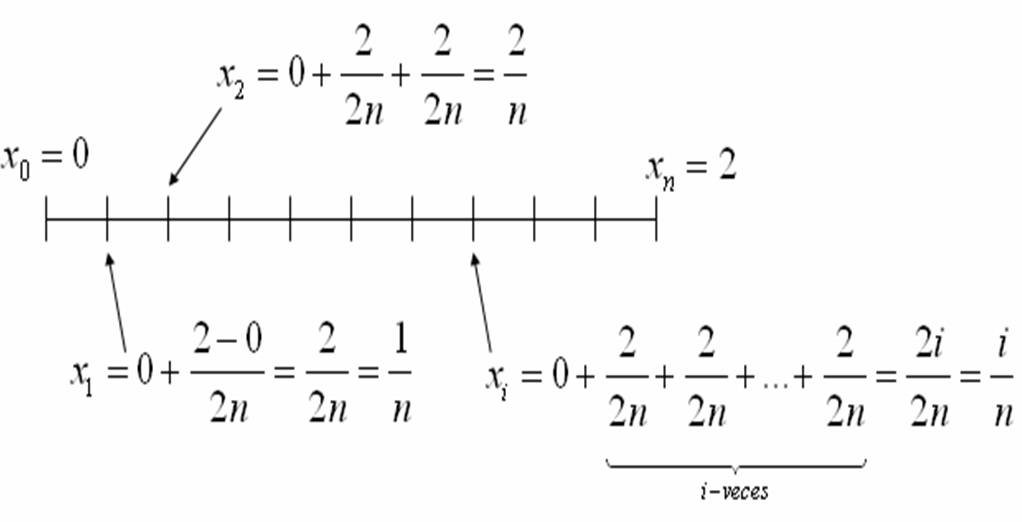

de esta manera se tiene que $\displaystyle{x_{i}=\frac{i}{n}}$ y
$\displaystyle{x_{i-1}=\frac{i-1}{n}}$. Mientras que para $[0,1]$ consideramos una
partición $P={y_{0},y_{1},…,y_{n}}$ con longitud
$\displaystyle{\frac{1-0}{n}=\frac{1}{n}}$ de esta manera se tiene que
$\displaystyle{y_{j}=\frac{j}{n}}$ y $\displaystyle{y_{j-1}=\frac{j-1}{n}}$.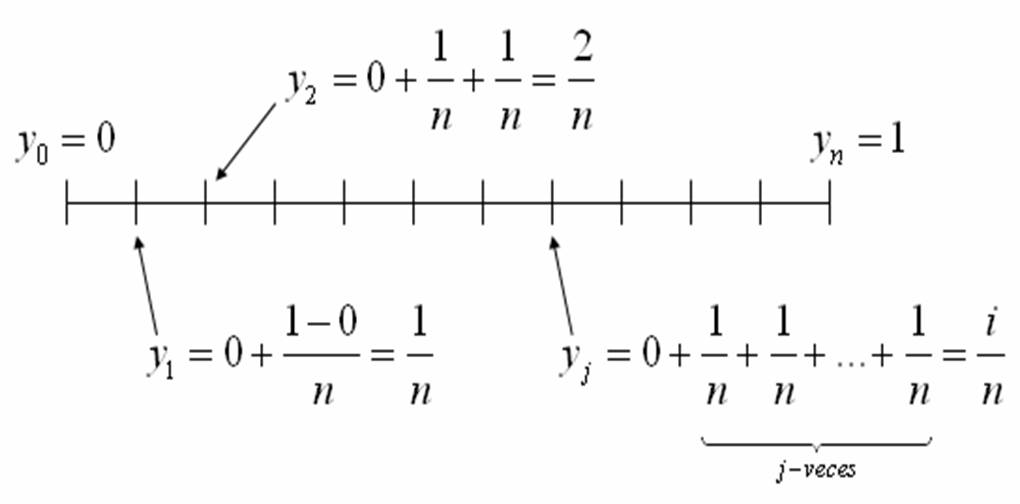

$\therefore$ Para todo rectángulo $R_{ij}$,
$M_{ij}=sup{f(x_{i,j})|x_{ij}\in
[x_{i-1},x:{i}]\times[y_{j-1},y_{j}]}=x_{i}+4y_{j}$ y
$m_{ij}=sup{f(x_{i,j})|x_{ij}\in
[x_{i-1},x:{i}]\times[y_{j-1},y_{j}]}=x_{i-1}+4y_{j-1}$
$\therefore$
$$\underline{S}(f,P)=\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(x_{i-1}+4y_{j-1}\right)\left(\frac{1}{n}\right)\left(\frac{1}{n}\right)=\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(\frac{i-1}{n}+4\frac{j-1}{n}\right)\left(\frac{1}{n}\right)\left(\frac{1}{n}\right)$$
$$=\left(\frac{1}{n^{2}}\right)\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(\frac{i-1}{n}+4\frac{j-1}{n}\right)=\left(\frac{1}{n^{3}}\right)\sum_{i=1}^{2n}\sum_{j=1}^{n}i+4j-5=\left(\frac{1}{n^{3}}\right)\sum_{i=1}^{2n}n(i-5)+4\left(n\left(\frac{n+1}{2}\right)\right)$$
$$=\left(\frac{1}{n^{2}}\right)\sum_{i=1}^{2n}(i-5)+2(n+1)=\left(\frac{1}{n^{2}}\right)\sum_{i=1}^{2n}i+2n-3=\left(\frac{1}{n^{2}}\right)\left(2n(2n-3)+\frac{2n(2n+1)}{2})\right)=$$
$$\left(\frac{1}{n}\right)\left(2(2n-3)+2n+1\right)=\left(\frac{1}{n}\right)(4n-6+2n+1)=\left(\frac{1}{n}\right)(6n-5)=6-\frac{5}{n}$$
$\therefore$
$$\underline{\int}R_{f}=\sup\underline{S}(f,P)=\lim_{n\rightarrow\infty}\underline{S}(f,P)= \lim_{n\rightarrow\infty} 6-\frac{5}{n}=6$$

Ahora bien para $\displaystyle{\overline{S}R_{f}}$

$\therefore$
$$\overline{S}(f,P)=\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(x_{i}+4y_{j}\right)\left(\frac{1}{n}\right)\left(\frac{1}{n}\right)=\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(\frac{i}{n}+4\frac{j}{n}\right)\left(\frac{1}{n}\right)\left(\frac{1}{n}\right)$$
$$=\left(\frac{1}{n^{3}}\right)\sum_{i=1}^{2n}\sum_{j=1}^{n}\left(i+4j\right)=\left(\frac{1}{n^{3}}\right)\sum_{i=1}^{2n}ni+4\left(\frac{n(n+1)}{2}\right)=\left(\frac{1}{n^{3}}\right)\left(n\left(\frac{2n(2n+1)}{2}\right)+2n\left(\frac{4n(n+1)}{2}\right)\right)$$
$$=\left(\frac{1}{ n^{3}}\right)(2n^{3}+n^{2}+4n^{3}+4n^{2})=2+\frac{1}{n}+4+\frac{4}{n}=6+\frac{5}{n}$$

$\therefore$
$$\overline{\int}R_{f}=\sup\overline{S}(f,P)=\lim_{n\rightarrow\infty}\overline{S}(f,P)= \lim_{n\rightarrow\infty} 6+\frac{5}{n}=6$$