Introducción
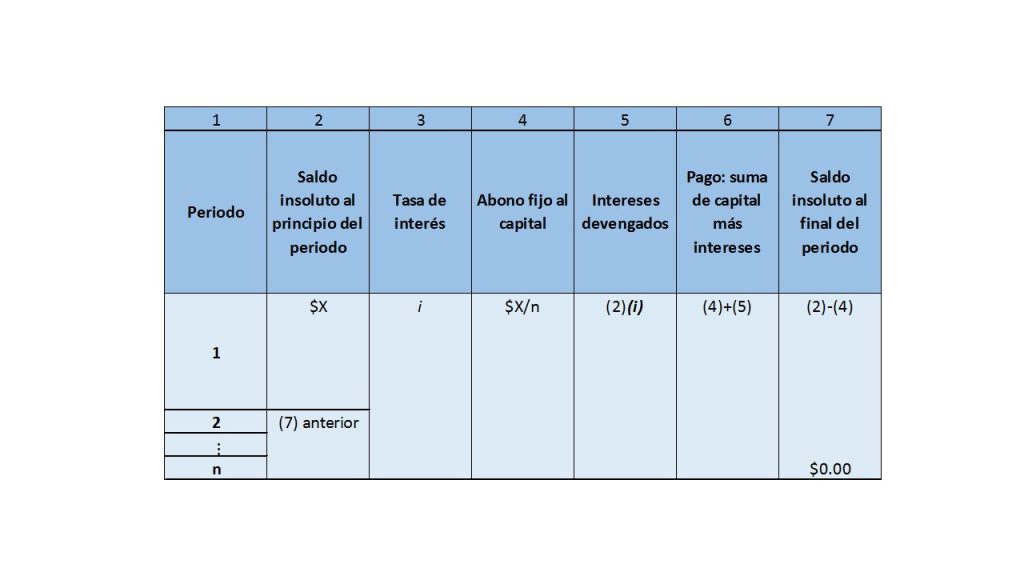
En este apartado, por fin se va analizar el comportamiento de una tabla de amortización, así como su construcción haciendo uso de los temas que se han venido manejando, así mismo, se verán las diferentes combinaciones que pueden haber entre ellas.
Concepto y descripción
Como se ha estado haciendo mención en temas anteriores, se pueden hacer combinaciones de las diferentes anualidades que se han estado estudiando, cada una de ellas puede ser utilizada para resolver alguna eventualidad en particular, dependiendo del contexto que se trate, por ello es importante hacer notar que, también se pueden construir tablas de amortización que describen el comportamiento de los pagos de un crédito que por su naturaleza y diseño, en determinadas ocasiones es necesario hacer que se combinen entre ellos.
Para mostrar el proceso de construcción de ésta tabla de amortización, se hará a través del siguiente ejemplo:
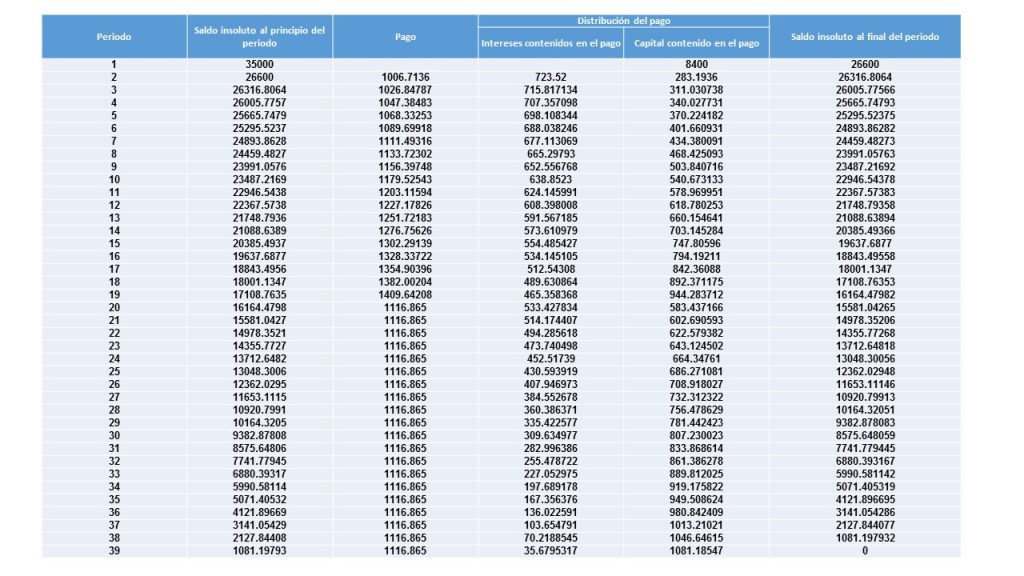
La empresa del señor Juan, desea dar mantenimiento a su parque vehicular, para hacerlo solicita un crédito por un monto de \$35 mil pesos, y planea hacer el contrato dando un anticipo por la cantidad de \$8,400, el saldo que falta por pagar, tiene considerado liquidarla de la siguiente manera:
El banco que le otorgó un crédito de \$26,600, se los prestó a cambio de una tasa del 38% anual, y el señor Juan realizará pagos mensuales por un monto de \$1006.7136, los cuales irán incrementando el 2% en cada periodo, durante dos años y medio.
Sin embargo, al cabo de un año y medio la empresa del señor Juan, quiere re-negociar la deuda, para que el saldo que aún falta por pagar, lo pueda liquidar en pagos mensuales iguales, situación que le cuesta una penalización por parte del banco, de una tasa de interés del 3.3%.
El señor Juan necesita conocer la tabla de amortización bajo éstas condiciones.
Para poder construir la tabla de amortización que nos pide el problema, se requiere calcular primero:
La cantidad a la que asciende el pago de primera cuota, el cual queda determinado por la siguiente expresión:
$$X=\left(\frac{26600}{\left(1-\left(\frac{1.02}{1.0272}\right)^{30}\right)}\right)(0.0272-0.02)$$
$$X=\left(\frac{26600}{\left(1-(0.9929907)^{30}\right)}\right)(0.0072)$$
$$X=\left(\frac{26600}{\left(1-(0.8097572)\right)}\right)(0.0072)$$
$$X=\left(\frac{26600}{0.1902428}\right)(0.0072)$$
$$X=1006.713653$$
Ejercicios resueltos
Ejercicio. Don Felipe quiera abrir una empresa de reparación de autos, para poder hacerlo solicita un crédito a un banco por la cantidad de dos millones y medio, el banco le cobra por dicho monto una tasa de interés del 1.5% mensual, y los planes del señor Felipe es poder pagarlo de la siguiente forma:
Lo realizará por 3 etapas. La primera consiste en diferir los pagos durante los primeros 3 meses, una vez transcurrido dicho tiempo, realizará 6 pagos de forma mensual y crecientes, iniciando una cantidad de \$100 mil pesos, los demás pagos se irán incrementando \20 mil pesos.
Durante la etapa 2, planea hacer 8 pagos mensuales iguales, de forma vencida, cada uno por la cantidad de \$180 mil pesos.
Por último, quiere hacer 5 pagos mensuales, los cuales irán decreciendo por una cantidad de \$15 mil pesos, y dará inicio con un pago por la cantidad de \$150 mil pesos. Una vez transcurridos 4 meses, planea hacer el último pago con el que quiere liquidar el monto que a ése momento falte.
Se requiere obtener la cantidad del último pago, así como la elaboración de la tabla de amortización.
Solución
El planteamiento gráfico de la solución a éste ejercicio se muestra a continuación:

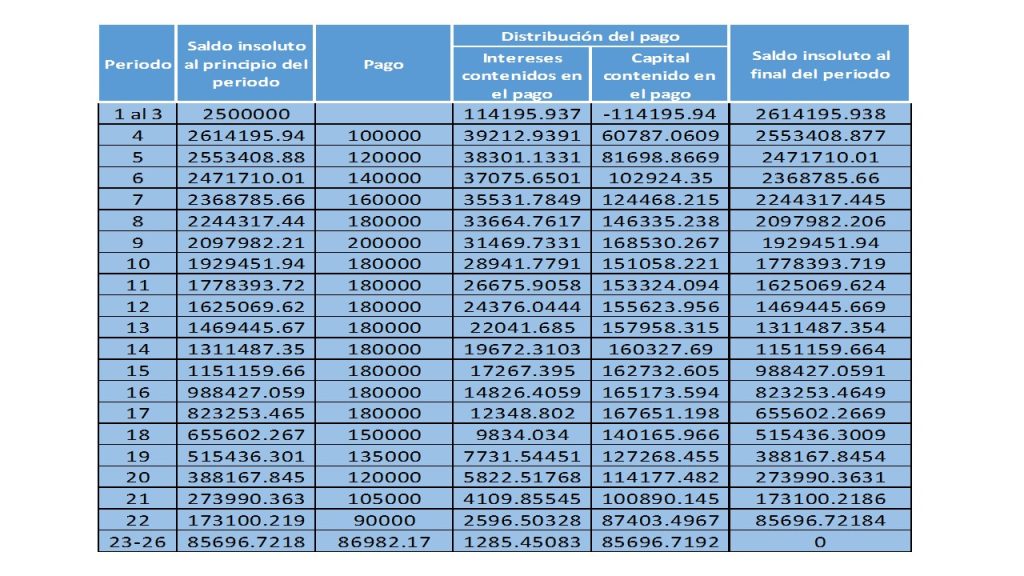
a continuación, se muestra su respectiva tabla de amortización:
Más adelante…
Hasta este momento se cuenta con las herramientas suficientes para aplicar los conocimientos sobre lo que son las anualidades y se ejemplificó la forma en que se pueden ir combinando, en el siguiente capítulo se abordará el tipo de tablas de amortización que involucran pagos de más anualidades, los cuales suelen presentarse en situaciones en las que las empresas tienen la necesidad de asentar ingresos adicionales por motivo de incremento en ventas, como lo son las temporadas navideñas, o alguna otra fecha que represente un ingreso adicional.
- Matemáticas Financieras
- Entrada anterior
- Entrada siguiente