Introducción

Hasta ahora, hemos estudiado la integral de Lebesgue para funciones definidas (en c.t.p.) de $\mathbb{R}^n$. Sin embargo, quizá como analogía con la integral de Riemann, es esperable que podamos definir la integral sobre conjuntos más generales, por ejemplo rectángulos o esferas. Esto es precisamente lo que estudiaremos en esta sección.

Definición y convenciones

Si queremos integrar una función $f$ sobre un conjunto $E$, una noción bastante natural es la siguiente:

Definición. Dada una función medible $f:\mathbb{R}^n\to [-\infty, \infty]$ y un conjunto medible $E\subseteq \mathbb{R}^n$, definimos la integral de $f$ sobre $E$ (cuando tenga sentido) como: $$\int_E f \ \mathrm{d}\lambda=\int f\cdot \chi_E \ \mathrm{d}\lambda.$$ Donde $\chi_E$ es la función característica de $E$.

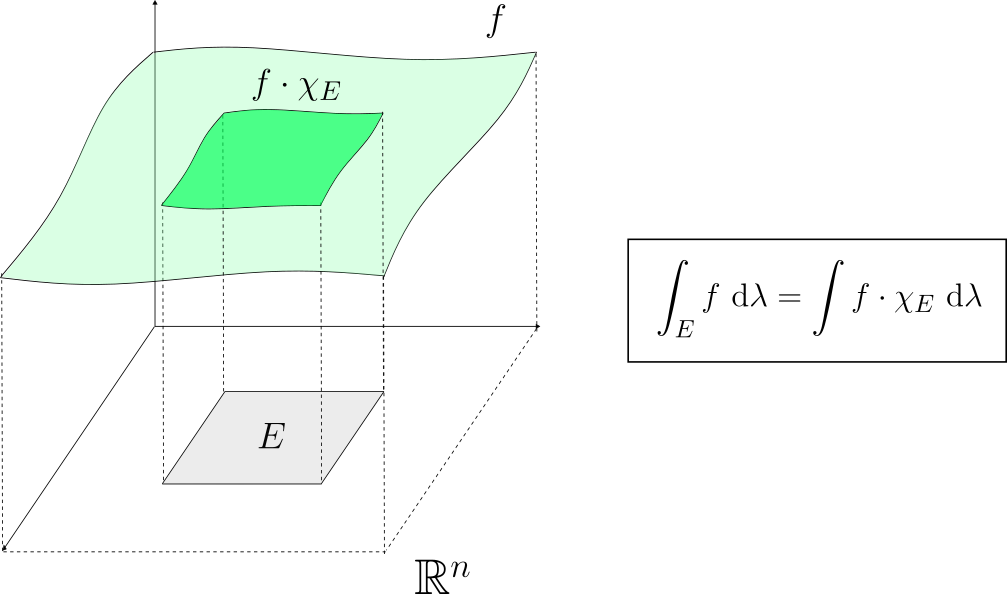
Si una función $f$ solamente está definida en casi todo punto de $E$, es decir, $f:E\setminus N \to [-\infty,\infty]$ (con $\lambda(N)=0$), podemos convenir que
\begin{equation*}
f\cdot\chi_E(x)=
\begin{cases}
f(x) & \text{si } x\in E\\
0 & \text{si } x\notin E
\end{cases}
\end{equation*} Diremos que $f$ es medible sobre $E$ si la función definida en c.t.p. $f\cdot\chi_E$ es medible. Definimos la integral de $f$ sobre $E$ como antes (siempre que tenga sentido).

Definición. Diremos que $f$ es integrable sobre $E$, si $f\chi_E\in L^1(\mathbb{R}^n)$, y lo denotaremos como $f\in L^1(E)$.

Ejemplos y casos particulares

Ejemplo. Como un caso particular, tenemos la integral sobre todo $\mathbb{R}^n$: $$\int_{\mathbb{R}^n} f \ \mathrm{d}\lambda=\int f\chi_{\mathbb{R}^n} \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$

$\triangle$

Ejemplo. Sea \begin{equation*}
f(x) =
\begin{cases}
\frac{x}{|x|} & \text{ si } x \neq 0 \\
0 & \text{ si } x = 0.
\end{cases} \end{equation*} Entonces $$\int_{[2,3]}f \ \mathrm{d}\lambda = \int f\chi_{[2,3]} \ \mathrm{d}\lambda=\int \chi_{[2,3]} \ \mathrm{d}\lambda=\lambda([2,3])=1;$$

\begin{align*}
\int_{(-1,1)}f \ \mathrm{d}\lambda &= \int f\chi_{(-1,1)} \ \mathrm{d}\lambda= \int (-1)\chi_{(-1,0)} \ \mathrm{d}\lambda+\int (1)\chi_{(0,1)} \ \mathrm{d}\lambda\\
&=-\lambda((-1,0))+\lambda((0,1))=0.
\end{align*}

$\triangle$

Las integrales sobre intervalos son particularmente frecuentes, así que conviene establecer notación especial para estas. Tomaremos prestada la notación usual para integrales de Riemann sobre intervalos. Esto no es al azar, como veremos más adelante, la integral de Riemann sobre un intervalo es un caso particular de la integral de Lebesgue.

Notación. Denotaremos las integrales sobre un intervalo $I\subseteq \mathbb{R}$ con extremos $a<b$, como $$\int_a^bf \ \mathrm{d}\lambda=\int_a^bf(x) \ \mathrm{d}x.$$ Observa que el tipo de intervalo (abierto, semicerrado, etc.) es irrelevante pues los extremos de un intervalo son conjuntos de medida cero.

Para ilustrar, las integrales del ejemplo anterior se reescribirían como: $$\int_2^3f \ \mathrm{d}\lambda; \ \ \ \ \ \int_{-1}^1f \ \mathrm{d}\lambda.$$ Respectivamente.

Ejemplo. La integral sobre cualquier conjunto de medida cero es cero. En efecto, si $f$ es medible sobre $E$ y $\lambda(E)=0$, tenemos que $f\chi_E=0$ en c.t.p. de $\mathbb{R}^n$ $\implies$ $\int_E f \ \mathrm{d}\lambda=\int f\chi_E \ \mathrm{d}\lambda=0$.

$\triangle$

Ejemplo. Si $f\in L^1(\mathbb{R}^n)$ $\implies$ $f\in L^1(E)$ para cualquier $E$ subconjunto medible, pues $|f\chi_E|\leq |f|$ $\implies$ $\int |f\chi_E| \ \mathrm{d}\lambda\leq \int |f| \ \mathrm{d}\lambda<\infty$.

Más generalmente, si $f\in L^1(F)$ y $E\subseteq F$ $\implies$ $f\in L^1(E)$, pues $|f\chi_E|\leq |f\chi_F|$.

El regreso es falso. Por ejemplo, la función constante $g\equiv 1$ cumple que $g\in L^1(E)$ para cualquier $E$ con medida finita pues $\int_E g \ \mathrm{d}\lambda=\int 1\chi_E \ \mathrm{d}\lambda=\lambda(E)<\infty$. Sin embargo, $g\notin L^1(\mathbb{R}^n)$, ya que $\int g \ \mathrm{d}\lambda=\infty$.

$\triangle$

Ejemplo. Cualquier función medible y acotada es integrable sobre un conjunto de medida finita: si $|f|\leq M$ sobre $E$, entonces $$\int_E |f| \ \mathrm{d}\lambda=\int |f\chi_E| \ \mathrm{d}\lambda\leq M \int \chi_E \ \mathrm{d}\lambda=M\lambda(E)<\infty.$$

$\triangle$

Propiedades de la integral sobre subconjuntos

Las siguientes propiedades son todas consecuencias sencillas de la definición y sus análogos para la integral en todo $\mathbb{R}^n$. Omitimos la demostración.

Proposición. Sean $A,B\in \mathcal{L}$ . Entonces:

1. Si $f,g\in L^1(A)$ y $a,b\in \mathbb{R}$, entonces $$\int_A af+bg \ \mathrm{d}\lambda=a\int_A f \ \mathrm{d}\lambda+b\int_A g \ \mathrm{d}\lambda.$$
2. Si $f=g$ en c.t.p. sobre $A$ y $f\in L^1(A)$ entonces $g\in L^1(A)$ con $$\int_A f \ \mathrm{d}\lambda=\int_A g \ \mathrm{d}\lambda.$$
3. Si $f\in L^1(A),L^1(B)$ y $\lambda(A\cap B)=0$ entonces $$\int_{A\cup B} f \ \mathrm{d}\lambda=\int_A f \ \mathrm{d}\lambda+\int_B f \ \mathrm{d}\lambda.$$
4. (Monotonía sobre funciones).) Si $f,g\in L^1(A)$ y $f\leq g$ entonces $$\int_A f \ \mathrm{d}\lambda \leq \int_A g \ \mathrm{d}\lambda.$$
5. (Monotonía sobre conjuntos). Si $f\in L^1(B)$ con $f\geq 0$ y $A\subseteq B$ entonces $f\in L^1(A)$ y $$\int_A f \ \mathrm{d}\lambda\leq \int_B f \ \mathrm{d}\lambda.$$
6. (Desigualdad del triángulo). $f\in L^1(A)$ $\iff$ $|f|\in L^1(A)$. Además $$ \left| \int_A f \ \mathrm{d}\lambda \right| \leq \int_A |f| \ \mathrm{d}\lambda.$$
7. (Convergencia monótona). Sea $0\leq f_1\leq f_2 \leq \dots$ una sucesión creciente de funciones medibles y no negativas sobre $A$. Entonce $\lim_{k\to \infty} f_k$ es medible con $$\lim_{k\to \infty} \int_A f_k \ \mathrm{d}\lambda=\int_A \lim f_k \ \mathrm{d}\lambda.$$
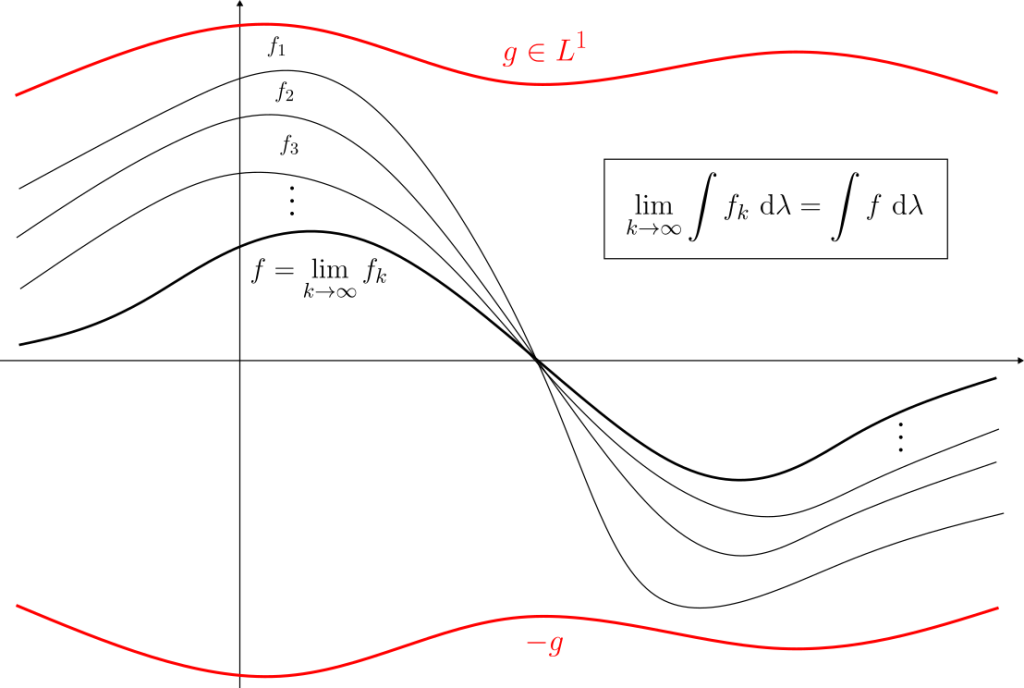
8. (Convergencia dominada). Sea $\{ f_k \}_{k=1}^{\infty} $ una sucesión de funciones medibles sobre $A$ tales que existe $g\in L^1(A)$ con: $$|f_k(x)|\leq g(x)$$ Para casi todo $x\in A$. Entonces $\lim f_k$ es integrable sobre $A$ con $$\lim_{k\to \infty} \int_A f_k \ \mathrm{d}\lambda=\int_A \lim f_k \ \mathrm{d}\lambda.$$

$\square$

Proposición (Aditividad numerable de la integral). Sean $E_1,E_2,\dots$ conjuntos medibles disjuntos y $E=\bigcup_{k=1}^{\infty}E_k$. Sea $f:E\to [-\infty,\infty]$ medible sobre $E$. Supongamos adicionalmente que ocurre alguna de las dos siguientes:

• $f\geq 0$.
• $f\in L^1(E)$.

Entonces $$\int_E f \ \mathrm{d}\lambda=\sum_{k=1}^{\infty}\int_{E_k} f \ \mathrm{d}\lambda.$$

Demostración. Para el primer caso:

\begin{align*}
\int_E f \ \mathrm{d}\lambda &= \int f\chi_E \ \mathrm{d}\lambda \\
&= \int \sum_{k=1}^{\infty} f\chi_{E_k} \ \mathrm{d}\lambda \\
&= \sum_{k=1}^{\infty} \int f\chi_{E_k} \ \mathrm{d}\lambda\\
&= \sum_{k=1}^{\infty} \int_{E_k} f \ \mathrm{d}\lambda
\end{align*}

En la segunda igualdad usamos $\chi_E=\sum_{k=1}^{\infty} \chi_{E_k}$, consecuencia de que los $E_k$ son ajenos. La tercera igualdad es debido a que la integral conmuta con sumas de funciones positivas.

Para el segundo caso, notemos que, similarmente al caso anterior: $$\sum_{k=1}^{\infty} \int |f|\chi_{E_k} \ \mathrm{d}\lambda=\int \sum_{k=1}^{\infty} |f|\chi_{E_k} \ \mathrm{d}\lambda=\int |f|\chi_{E} \ \mathrm{d}\lambda=\int_E |f| \ \mathrm{d}\lambda<\infty.$$

Lo que garantiza que podemos intercambiar sumas con integrales:

$$\sum_{k=1}^{\infty} \int_{E_k} f \ \mathrm{d}\lambda=\sum_{k=1}^{\infty} \int f\chi_{E_k} \ \mathrm{d}\lambda=\int \sum_{k=1}^{\infty} f\chi_{E_k} \ \mathrm{d}\lambda=\int_E f \ \mathrm{d}\lambda.$$
Como queríamos probar.

$\square$

Continuidad absoluta

Veamos ahora un resultado «de continuidad» para la integral de funciones en $L^1$. En cierto modo nos dice que «la integral sobre conjuntos pequeños es uniformemente pequeña», o alternativamente, que una función integrable no puede acumular su «masa» sobre conjuntos arbitrariamente pequeños.

Teorema (Continuidad absoluta respecto al dominio). Sea $f\in L^1(\mathbb{R}^n)$ y $\varepsilon>0$. Entonces existe $\delta>0$ tal que si $E\in \mathcal{L}$ es medible con $\lambda(E)<\delta$ entonces $$\left| \int_E f \ \mathrm{d}\lambda \right|<\varepsilon.$$

Demostración. Supongamos primero que $f\geq 0$. Por definición, existe una función simple $s\in S$ tal que $0\leq s \leq f$ y $$\int s \ \mathrm{d}\lambda > \int f \ \mathrm{d}\lambda-\frac{\varepsilon}{2}.$$

Como $s$ es simple, en particular es acotada (sólo toma una cantidad finita de valores), así que existe $C>0$ tal que $$s(x)\leq C \ \ \ \forall x\in \mathbb{R}^n.$$

Luego:

\begin{align*}
\int_E f \ \mathrm{d}\lambda &= \int_E s \ \mathrm{d}\lambda + \int_E (f-s) \ \mathrm{d}\lambda \\
&\leq \int_E C \ \mathrm{d}\lambda+\int_{\mathbb{R}
^n} (f-s) \ \mathrm{d}\lambda \\
&\leq \int_E C \ \mathrm{d}\lambda+\int_{\mathbb{R}
^n} f \ \mathrm{d}\lambda – \int_{\mathbb{R}
^n} s \ \mathrm{d}\lambda \\
&< C\lambda(E)+\frac{\varepsilon}{2}.
\end{align*}

Así que, si tomamos cualquier $E$ con $\lambda(E)< \frac{\varepsilon}{2C}=\delta$, se cumple lo buscado.

El caso general se sigue del caso no negativo aplicado a $|f|$ y la desigualdad del triángulo.

$\square$

Más adelante…

Veremos la relación que existe entre la integral de Riemann y la integral de Lebesgue. Veremos que la integral de Lebesgue es una generalización de la integral de Riemann. Esto nos permitirá usar todas las herramientas conocidas de la integral de Riemann (cuando apliquen) como el teorema fundamental del cálculo para evaluar integrales.

Tarea moral

• Sea $f$ una función definida (en c.t.p.) sobre $E$: $f:E\setminus N\to [-\infty,\infty]$ (con $\lambda(N)=0$). Demuestra que las siguientes son equivalentes:
  • $f$ es medible sobre $E$.
  • Para cada $t\in [-\infty, \infty]$, $f^{-1}([-\infty,t])\cap E\in \mathcal{L}$.
  • $f^{-1}(\pm\infty)\in \mathcal{L}$ y para cualquier $B\in \mathcal{B}$ conjunto de Borel, $f^{-1}(B)\cap E\in \mathcal{L}$.
  • $f$ es $\mathcal{L}_{E\setminus N}$-medible, donde $\mathcal{L}_{E\setminus N}$ denota la restricción sobre $E\setminus N$ de la $\sigma$-álgebra de conjuntos Lebesgue-medibles.
• Verifica las propiedades de las integrales sobre subconjuntos de la primera proposición.
• Sea $E$ un conjunto medible. Sea $f$ una función medible sobre $E$. Supongamos que existe $M>0$ tal que $\{x\in E \ | \ f(x)>M \}$ es nulo.
  • Prueba que si $\lambda(E)<\infty$, entonces $f\in L^1(E)$.
  • ¿Se cumple lo anterior si $\lambda(E)=\infty$?
• (teorema de Convergencia acotada). Sea $E$ un conjunto medible con $\lambda(E)<\infty$. Sea $\{ f_k \}_{k=1}^{\infty} $ una sucesión de funciones medibles sobre $E$ tales que existe $0\leq M <\infty$ con: $$|f_k(x)|\leq M$$ Para casi todo $x\in E$. Demuestra que $\lim f_k$ es integrable sobre $E$ con $$\lim_{k\to \infty} \int_E f_k \ \mathrm{d}\lambda=\int_E \lim f_k \ \mathrm{d}\lambda.$$ [SUGERENCIA: Esto es consecuencia del teorema de la convergencia dominada. ¿Qué función domina a la sucesión?].
• Sea $f\in L^1(\mathbb{R})$. Definamos $$F(x)=\int_0^x f(t) \ \mathrm{d}t.$$ Con la convención: $\int_b^a f(t) \ \mathrm{d}t=-\int_a^b f(t) \ \mathrm{d}t$ si $a<b$. Demuestra que $F$ es una función continua. ¿Es $F$ una función diferenciable?
• Sea $f\in L^1(\mathbb{R}^n)$. Demuestra que para cualquier $\varepsilon>0$, existe $R$ suficientemente grande tal que $$\left| \int_{\mathbb{R}^n\setminus B_R(0)} f \ \mathrm{d}\lambda \right|<\varepsilon.$$ Donde $B_R(0)$ denota la bola de radio $R$ con centro en el orígen.

Introducción

El concepto de «casi donde sea» (o «en casi todo punto») refiere que dos objetos matemáticos (por ejemplo funciones) pueden considerarse equivalentes si coinciden excepto en un conjunto de medida cero. En términos de integración, esto significa que cualquier propiedad definida mediante integrales permanece invariante aunque las funciones difieran en conjuntos «irrelevantes». Este concepto simplifica problemas al ignorar comportamientos excepcionales sin importancia global.

Algunos Lemas

La siguiente serie de Lemas refuerzan la idea de que, a ojos de la integral, dos objetos son «iguales» si coinciden salvo en conjuntos de medida cero.

Lema. Sea $f:\mathbb{R}^n\to[-\infty,\infty]$ una función medible. Si $g:\mathbb{R}^n\to [-\infty,\infty]$ es una función tal que $Z=\{ x \ | \ f(x)\neq g(x) \}$ es un conjunto nulo, entonces $g$ es medible.

Demostración. Para cualquier $t\in \mathbb [-\infty,\infty]$, podemos escribir:

$$g^{-1}([-\infty,t])=(f^{-1}([-\infty,t])\setminus B)\cup A.$$

Donde $$A=\{ x \ | \ g(x)\in [-\infty,t]; \ g(x)\neq f(x) \}$$ Y $$B=\{ x \ | \ f(x)\in [-\infty,t]; \ g(x)\neq f(x) \}.$$

Claramente $A,B\subseteq Z$. Luego $\lambda(A)=\lambda(B)=\lambda(Z)=0$ $\implies$ $A$ y $B$ son medibles (cualquier conjunto nulo es medible). Como $f^{-1}([-\infty,t])$, $A$ y $B$ son medibles, se sigue que $g^{-1}([-\infty,t])$ es un conjunto medible.

$\square$

Lema. Si $f:\mathbb{R}^n \to [0,\infty]$ es una función no negativa tal que $f(x)=0$ salvo un conjunto de medida cero, entonces $$\int f \ \mathrm{d}\lambda = 0.$$

Demostración. Por el lema anterior, $f$ es medible (es 0 ). Por no negatividad, $\int f \ \mathrm{d}\lambda\geq 0$.

Si $\int f \ \mathrm{d}\lambda>0$, por definición de la integral, existiría una función simple $s\in S$ tal que $s\leq f$ y $$0<\int s \ \mathrm{d}\lambda\leq \int f \ \mathrm{d}\lambda.$$ Al ser simple, podemos escribir $s=\sum_{k=1}^{m}\alpha_k\chi_{A_k}$, con $\alpha_1,\dots,\alpha_m>0$ y $A_1,\dots,A_m$ ajenos. Como $\int s \ \mathrm{d}\lambda=\sum_{k=1}^{m}\alpha_k\lambda(A_k)>0$, necesariamente existiría algún $A_r$ con $\lambda(A_r)>0$. Sin embargo, esto implica que $f\geq \alpha_r>0$ sobre $A_r$, lo que contradice que $f=0$ salvo un conjunto nulo.

Por tanto, la única posibilidad es $\int f \ \mathrm{d}\lambda=0$.

$\square$

De hecho, podemos relajar la condición $f\geq 0$ en el Lema anterior:

Corolario. Si $f:\mathbb{R}^n \to [-\infty,\infty]$ es una función tal que $f(x)=0$ salvo un conjunto de medida cero, entonces $f\in L^1(\mathbb{R}^n)$ y $$\int f \ \mathrm{d}\lambda = 0.$$

Demostración. $f$ es medible por el primer Lema. Aplicando el lema anterior a $f_+$ y $f_-$ por separado, se sigue que $\int f \ \mathrm{d}\lambda=\int f_+ \ \mathrm{d}\lambda-\int f_- \ \mathrm{d}\lambda=0-0=0.$

$\square$

Proposición (Insensibilidad de la integral).

• Sea $f:\mathbb{R}^n\to [0,\infty]$ una función medible no negativa. Si $g:\mathbb{R}^n\to [-\infty,\infty]$ es tal que el conjunto $Z=\{ x \ | \ f(x)\neq g(x) \}$ es nulo, entonces $g$ es medible y $$\int g \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$
• Sea $f:\mathbb{R}^n\to [-\infty,\infty]$ una función en $L^1(\mathbb{R}^n)$. Si $g:\mathbb{R}^n\to [-\infty,\infty]$ es tal que el conjunto $Z=\{ x \ | \ f(x)\neq g(x) \}$ es nulo, entonces $g\in L^1(\mathbb{R}^n)$ y $$\int g \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$

Demostración. Los lemas anteriores aseguran que $g$ es medible en ambos casos.

Para la primera parte, supongamos primero que $g$ es no negativa. Podemos escribir $f=f\cdot\chi_{Z^c}+f\cdot\chi_Z$ y $g=f\cdot\chi_{Z^c}+g\cdot\chi_Z$. En ambos casos, la función de la derecha es 0 salvo quizá un conjunto nulo ($Z$). Entonces:

\begin{align*}
\int f \ \mathrm{d}\lambda &= \int f\cdot\chi_{Z^c} \ \mathrm{d}\lambda+\int f\cdot\chi_Z \ \mathrm{d}\lambda \\
&= \int f\cdot\chi_{Z^c} \ \mathrm{d}\lambda+0 \\
&= \int g\cdot\chi_{Z^c} \ \mathrm{d}\lambda+0 \\
&= \int g\cdot\chi_{Z^c} \ \mathrm{d}\lambda + \int g\cdot\chi_{Z} \ \mathrm{d}\lambda \\
&= \int g \ \mathrm{d}\lambda
\end{align*}

Para el caso general, podemos escribir $g=g_+-g_-$, donde $g_+=f$ y $g_-=0$ salvo en conjuntos de medida cero. Usando el caso anterior y los lemas:

$$\int g \ \mathrm{d}\lambda=\int g_+ \ \mathrm{d}\lambda-\int g_- \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda-0=\int f \ \mathrm{d}\lambda.$$

Para la segunda parte, notemos que $g-f=0$ salvo un conjunto de medida cero. Así $(g-f)\in L^1(\mathbb{R}^n)$ con $$\int (g-f) \ \mathrm{d}\lambda=0.$$
Luego, por linealidad, $g=(g-f)+f\in L^1(\mathbb{R}^n)$ y $$\int g \ \mathrm{d}\lambda=\int (g-f) \ \mathrm{d}\lambda+\int f \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$

$\square$

El concepto de casi donde sea

Definición. Decimos que una propiedad $\mathcal{P}$ en $\mathbb{R}^n$ se satisface «casi donde sea» ó «para casi todo $x$» ó «para casi todo punto«, si el conjunto $$A=\{ x\in \mathbb{R}^n \ | \ \mathcal{P}(x) \text{ NO se satisface } \}.$$

Es nulo.

Generalmente abreviaremos la expresión «en casi todo punto» y sus equivalentes como c.t.p. En la literatura inglesa se suele denotar como a.e. (por almost everywhere).

Ejemplo. Casi todos los números reales son irracionales. El conjunto de racionales $\mathbb{Q}$ es de medida cero al ser numerable.

$\triangle$

Ejemplo. Podemos reescribir la proposición de insensibilidad de la siguiente forma: Si $f\in L^1$ y $f=g$ en c.t.p, entonces $g\in L^1$ y $$\int f \ \mathrm{d}\lambda=\int g \ \mathrm{d}\lambda.$$ Esto sugiere que, a ojos de la integral, dos funciones iguales en c.t.p. son «indistinguibles».

$\triangle$

Funciones definidas en casi todo punto

Otra situación que ocurre con frecuencia es que sólo podamos asegurar que una función esté definida en c.t.p. (el último teorema de esta sección es un ejemplo de esto). Sin embargo, como sugieren los teoremas anteriores, esto es suficiente para poder hablar de su integral. Procedamos de manera precisa:

Definición. Sea $f:X\subseteq \mathbb{R}^n \to [-\infty,\infty]$ una función definida en casi todo punto (c.t.p.) de $\mathbb{R}^n$ (i.e. $\lambda(\mathbb{R}^n \setminus N)=0$). Decimos que $f$ es medible si existe una extensión medible de $f$, es decir, $g:\mathbb{R}^n\to[-\infty, \infty]$ tal que para todo $x\in X$: $$f(x)=g(x).$$ Definimos la integral de $f$ como $$\int f \ \mathrm{d}\lambda=\int g \ \mathrm{d}\lambda.$$ (Siempre que ésta tenga sentido).

Observación. Hay que notar que si $f$ admite una extensión medible, entonces cualquier extensión de $f$ será medible (primer lema de la entrada). Además, la integral no depende de la extensión tomada (por insensibilidad). Por esta razón, típicamente tomamos la «extensión por cero», es decir, la extensión que vale cero en los puntos donde $f$ no está definida originalmente.

Por todo lo anterior, no hace daño extender nuestro concepto de función medible: cada que nos refiramos a una «función medible sobre $\mathbb{R}^n$», admitiremos la posibilidad de que sea una función definida en casi todo punto de $\mathbb{R}^n$. Es inmediato ver que las propiedades de las funciones medibles también se satisfacen para las funciones medibles definidas en casi todo punto.

Convergencia en casi todo punto

Definición. Sea $\{ f_k\}_{k=1}^{\infty}$ una sucesión de funciones definidas en casi todo punto de $\mathbb{R}^n$ (i.e. $\lambda(\mathbb{R}^n \setminus N)=0$). Decimos que $\{ f_k\}_{k=1}^{\infty}$ converge en casi todo punto a $f$, si existe un conjunto de medida cero $N$ tal que para todo $x\in \mathbb{R}^n\setminus N$ $$f_k(x) \longrightarrow f(x).$$

Observación. La convergencia puntual implica la convergencia en casi todo punto. El regreso no necesariamente es cierto (tarea moral).

Observación. El límite de funciones medibles (definidas en c.t.p.) es una función medible (definida en c.t.p.). Para ver esto, basta redefinir $f_1,f_2, \dots,f$ por $0$ sobre los puntos donde no están definidas o no hay convergencia puntual (que es un conjunto de medida cero) y observar que la nueva sucesión converge puntualmente a una función igual en casi todo punto a $f$ (que será medible al ser el límite de funciones medibles).

Observación. En general los límites en casi todo punto no son únicos. Por ejemplo, cualquier función que converge a $0$ en c.t.p. también converge a $\chi_{\mathbb{Q}}$ en c.t.p. pues $\chi_{\mathbb{Q}}=0$ en c.t.p. Lo que sí podemos asegurar es que los límites son únicos salvo conjuntos de medida cero (tarea moral).

Generalización de los Teoremas de convergencia

Podemos dar generalizaciones de los teoremas de convergencia en las que consideremos convergencia en casi todo punto. Por ejemplo, para el teorema de convergencia dominada tendríamos lo siguiente.

Proposición (Convergencia dominada versión c.t.p.) Sean $f_1,f_2,\dots$ funciones medibles definidas en c.t.p. de $\mathbb{R}^n$, tales que

$$\lim_{k\to \infty} f_k(x)$$

Existe para casi todo $x\in \mathbb{R}^n$. Supongamos además que existe una función $g\in L^1$ definida en c.t.p con $$|f_k(x)|\leq g(x)$$
Para casi todo $x\in \mathbb{R}^n$ y para todo $k\in \mathbb{N}$. Entonces $$\int \left( \lim_{k\to \infty} f_k \right) \ \mathrm{d}\lambda=\lim_{k\to \infty} \int f_k \ \mathrm{d}\lambda.$$

Demostración. Sea $Z$ el conjunto de $x$ tales que: O bien $f_k(x)$ no está definida para algún $k$; o bien $\lim f_k(x)$ no existe; o bien $|f_k|(x)>g(x)$ para algún $k$. Como podemos expresar a $Z$ como una unión numerable de conjuntos nulos, el propio $Z$ debe ser nulo.

Podemos redefinir las $f_k$ y $g$ de tal manera que valgan 0 sobre $Z$. Esto no afecta las propiedades en c.t.p. ni los valores de ninguna integral, pero nos deja con las hipótesis clásicas del teorema de la convergencia dominada. El resultado se sigue de aplicar el teorema de la convergencia dominada usual sobre estas nuevas funciones y luego apelar nuevamente a la insensibilidad de la integral.

$\square$

Podemos dar generalizaciones similares para los teoremas de convergencia monótona y el Lema de Fatou. Las demostraciones son similares. A partir de ahora no haremos distinción entre las versiones usuales y en c.t.p. de estos teoremas.

Intercambio de Sumas con Integrales

El siguiente resultado es relevante. Como adelantamos, es un ejemplo en el que sólo podemos asegurar que una función esté definida en c.t.p.

Teorema. Sean $f_1,f_2,\dots$ funciones en $L^1(\mathbb{R}^n)$, tales que $$\sum_{k=1}^{\infty}\int |f_k| \ \mathrm{d}\lambda<\infty.$$ Entonces $$\sum_{k=1}^{\infty} f_k(x)$$ Existe para casi todo $x\in \mathbb{R}^n$ y además $$\int \left( \sum_{k=1}^{\infty}f_k\right) \ \mathrm{d}\lambda=\sum_{k=1}^{\infty} \int f_k \ \mathrm{d}\lambda.$$

Demostración. Sea $g=\sum_{k=1}^{\infty}|f_k|$. Ésta es una función medible y no negativa. Como consecuencia del Teorema de la convergencia monótona tenemos:

$$\int g \ \mathrm{d}\lambda= \int \sum_{k=1}^{\infty}|f_k| \ \mathrm{d}\lambda=\sum_{k=1}^{\infty}\int |f_k| \ \mathrm{d}\lambda<\infty.$$ $$\implies g\in L^1.$$ Como $g$ es integrable, sabemos que $g<\infty$ en c.t.p. $\implies$ la serie $\sum_{k=1}^{\infty}f_k(x)$ converge absolutamente para casi todo $x\in \mathbb{R}^n$ (en particular converge para casi todo $x\in \mathbb{R}^n$). Además, es claro que para cada $N\in \mathbb{N}$: $|\sum_{k=1}^{N}f_k(x)|\leq \sum_{k=1}^{\infty}|f_k|(x)= g(x)$ para casi todo $x$. Aplicando el teorema de la convergencia dominada sobre la sucesión de sumas parciales $\sum_{k=1}^{N}f_k$ concluimos: $$\int \left( \sum_{k=1}^{\infty}f_k\right) \ \mathrm{d}\lambda=\sum_{k=1}^{\infty} \int f_k \ \mathrm{d}\lambda.$$

$\square$

Más adelante…

Definiremos la integral sobre subconjuntos de $\mathbb{R}^n$ y sus principales propiedades.

Tarea moral

• Demuestra que los límites en casi todo punto son únicos salvo conjuntos de medida cero, es decir, que si una sucesión $\{ f_k\}_{k=1}^{\infty}$ converge en c.t.p. a $f_1$ y a $f_2$, entonces $f_1=f_2$ en c.t.p.
• Sea $f_k=\chi_{[0,\frac{1}{k}]}$. ¿A que función converge puntualmente la sucesión $f_k$? ¿La sucesión converge en c.t.p. a $0$?
• Enuncia y demuestra una versión en casi todo punto del Teorema de la convergencia monótona.
• Enuncia y demuestra una versión en casi todo punto del Lema de Fatou.
• Sean $f,g:\mathbb{R}^n\to \mathbb{R}$ funciones continuas e iguales en casi todo punto. Prueba que de hecho $f=g$ sobre todo $\mathbb{R}^n$.

Introducción

Estamos en condiciones de enunciar y demostrar otro de los teoremas más importantes en la teoría de integración de Lebesgue: El teorema de la convergnecia Dominada. Éste nos garantiza condiciones «relativamente débiles» bajo las cuales podemos intercambiar límites e integrales. La gracia de este teorema es que aplica para funciones medibles de todo tipo (no necesariamente positivas o crecientes) siempre que podamos encontrar alguna función en $L^1$ que «domine» en valor absoluto a todas las demás.

Teorema de la convergencia dominada. Sea $f_1,f_2,f_3,\dots$ una sucesión de funciones medibles en $\mathbb{R}^n$ tales que : $$\lim_{k\to \infty}f_k(x)$$ Existe para todo $x\in \mathbb{R}^n$, y existe una función $g\in L^1$ tal que \begin{equation}|f_k(x)|\leq g(x) \end{equation} Para todo $x\in \mathbb{R}^n$ y $k\in \mathbb{N}$. Entonces $f\in L^1$ y $$\int \left( \lim_{k\to \infty} f_k \right) \ \mathrm{d} \lambda = \lim_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$

Demostración. Sea $$f=\lim_{k\to \infty} f_k.$$ Ésta es medible al ser el límite de funciones medibles. Más aún, por (1) se sigue que $$0\leq |f|\leq g.$$ Entonces $|f|$ (y en particular $f$) es integrable.

Observemos que la función $g+ f_k$ es medible y no negativa para todo $k$. Aplicando el Lema de Fatou:

$$\int (g+ f) \ \mathrm{d} \lambda\leq \liminf_{k\to \infty} \int (g+ f_k) \ \mathrm{d} \lambda$$
$$\implies \int g \ \mathrm{d} \lambda + \int f \ \mathrm{d} \lambda \leq \int g \ \mathrm{d} \lambda + \liminf_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$
Restando $\int g \ \mathrm{d} \lambda<\infty$ de ambos lados de la desigualdad anterior obtenemos $$ \int f \ \mathrm{d} \lambda \leq \liminf_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$

Similarmente, aplicando el Lema de Fatou a las funciones $g-f_k\geq 0$ resulta $$\int (g- f) \ \mathrm{d} \lambda\leq \liminf_{k\to \infty} \int (g- f_k) \ \mathrm{d} \lambda$$ $$\implies \int g \ \mathrm{d} \lambda – \int f \ \mathrm{d} \lambda \leq \int g \ \mathrm{d} \lambda – \limsup_{k\to \infty} \int f_k \ \mathrm{d} \lambda.$$ $$\implies \limsup_{k\to \infty} \int f_k \ \mathrm{d} \lambda \leq \int f \ \mathrm{d} \lambda.$$

(En el segundo renglón usamos que $\liminf_k -a_k=-\limsup a_k$). Combinando las desigualdades obtenidas concluimos que $$ \int f \ \mathrm{d}\lambda \leq \liminf_{k\to \infty} \int f_k \ \mathrm{d} \lambda \leq \limsup_{k\to \infty} \int f_k \ \mathrm{d} \lambda \leq \int f \ {d}\lambda. $$ Es decir, $\lim_k \int f_k \ \mathrm{d}\lambda$ existe y es igual a $$\lim_{k\to \infty} \int f_k \ \mathrm{d} \lambda=\int f \ \mathrm{d} \lambda.$$

$\square$

Algunos ejercicios resueltos

Para fijar ideas, veamos un par de ejercicios resueltos.

Ejercicio. Sea $f\in L^1(\mathbb{R}^n)$ y $A_1\subseteq A_
2\subseteq \dots$ una sucesión creciente de conjuntos medibles tales que $\mathbb{R}^n=\bigcup_{k=1}^{\infty} A_k$. Demuestra que $$\lim_{k\to \infty} \int f\cdot \chi_{A_k} \ \mathrm{d}\mu=\int f \ \mathrm{d}\mu.$$

Solución. Las funciones $f\cdot \chi_{A_k}$ son medibles al ser producto de funciones medibles. Más aún, son integrables pues $$|f\cdot\chi_{A_k}|\leq |f| \ \ \ \ \ \forall k\in \mathbb{N} .$$ Como $f\in L^1$ $\implies$ $|f|\in L^1$, así que el estimado anterior nos dice que podemos «dominar» las funciones $f\cdot \chi_{A_k}$ por la función $g=|f|\in L^1$.
Ahora, como $\bigcup_{k=1}^{\infty} A_k=\mathbb{R}^n$, para cada $x\in \mathbb{R}^n$, existe algún entero $M_x$ suficientemente grande tal que $x\in A_{k}$ para todo $k\geq M_x$. Esto nos dice que $$f(x)\cdot \chi_{A_k}(x)=f(x)\cdot 1 =f(x) \ \ \ \ \ \forall k\geq M_x.$$ Como lo anterior se satisface para cualquier $x\in \mathbb{R}^n$, concluimos que $$\lim_{k\to \infty} (f\cdot \chi_{A_k})=f.$$ Finalmente, aplicando el teorema de la convergencia dominada a la sucesión de funciones $f\cdot \chi_{A_k}$ (tomando $|f|=g\in L^1$ como la función que «domina» a la sucesión), concluimos que $$\lim_{k\to \infty} \int f\cdot \chi_{A_k} \ \mathrm{d}\mu=\int f \ \mathrm{d}\mu.$$

$\triangle$

Observación. En el lenguaje de integración sobre subconjuntos, el resultado anterior se reescribe como: $$\lim_{k\to \infty}\int_{A_k}f \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$

Ejercicio. Sea $f\in L^1(\mathbb{R}^n)$. Demuestra que $$\lim_{k\to \infty} \int f(x)e^{-\frac{|x|^2}{k}} \ \mathrm{d}x = \int f(x) \ \mathrm{d}x.$$

Solución. Consideremos la sucesión de funciones $f_k(x)=f(x)e^{-\frac{|x|^2}{k}}$.

Como $e^{-\frac{|x|^2}{k}}\leq e^0=1$, entonces $|f_k(x)|\leq |f(x)|$ para $k=1,2,\dots$. Es decir, la función $|f|\in L^1$ domina a cada una de las $f_k$. Además $$\lim_{k\to \infty} f_k(x)=f(x)\lim_{k\to \infty} e^{-\frac{|x|^2}{k}} = f(x)\cdot e^0 = f(x).$$ Para todo $x\in \mathbb{R}^n$. Aplicando el teorema de la convergencia dominada:
$$\lim_{k\to \infty} \int f(x)e^{-\frac{|x|^2}{k}} \ \mathrm{d}x= \lim_{k\to \infty} \int f_k(x) \ \mathrm{d} x=\int \left( \lim_{k\to \infty} f_k(x) \right) \ \mathrm{d}x=\int f(x) \ \mathrm{d}x.$$

$\triangle$

Veamos ahora un ejemplo un poco más sofisticado, en el que encontrar la función integrable que «domina» a la sucesión no es del todo inmediata.

Ejercicio. Calcula $$\lim_{k\to \infty} \int_{\mathbb{R}}\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right) \ \mathrm{d}x.$$

Solución. Consideremos la sucesión $f_k(x)=\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right)$. Notemos que para cada $x\in \mathbb{R}$: \begin{equation}\lim_{k\to \infty} f_k(x)=\lim_{k\to \infty}\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right)=e^{-x^2}\sin(0)=0.\end{equation}

(Recuerda que $e^{-x}=\lim_{k\to \infty}\left( 1+\frac{x}{k} \right)^{-k}$). Así que si somos capaces de encontrar una función $g\in L^1$ que domine a la sucesión $f_k$, por el teorema de la convergencia dominada tendríamos que $$\lim_{k\to \infty}\int_{\mathbb{R}}f_k(x) \ \mathrm{d}x=\int 0 \ \mathrm{d}x=0.$$

Proponemos $$g(x)=\frac{1}{1+x^2}.$$

• Veamos que $|f_k(x)|\leq \frac{1}{1+x^2}$ para todo $x\in \mathbb{R}$ y $k\in \mathbb{N}$.

Como $|\sin(x)|\leq 1$ $\forall x$, tenemos que $$|f_k(x)|=\left| \left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right) \right|\leq \left(1+ \frac{x^2}{k} \right)^{-k}.$$

Así que es suficiente probar que $\forall x\in \mathbb{R}$ y $k\in \mathbb{N}$: $$\left(1+ \frac{x^2}{k} \right)^{-k}\leq \frac{1}{1+x^2}$$ $$\iff 1+x^2\leq \left(1+ \frac{x^2}{k} \right)^{k}.$$ Ésto último es inmediato por el teorema del binomio. Los primeros términos de $\left(1+\frac{x^2}{k}\right)^k$ son $1+\binom{k}{1}\left( \frac{x^2}{k}\right)+\dots=1+x^2+\dots$

• Veamos ahora que $g(x)=\frac{1}{1+x^2}\in L^1(\mathbb{R})$.

Más adelante, cuando veamos la equivalencia entre integral de Lebesgue e integral de Riemann, seremos capaces de calcular el valor exacto de dicha integral con muy poco trabajo. Por el momento, podemos estimar la integral con una serie convergente.

Notemos que $0\leq g(x)=\frac{1}{1+x^2}\leq 1$ $\forall x\in \mathbb{R}$. Más aún, si $|x|\geq N$ $\implies$ $|g(x)|=\frac{1}{1+x^2}\leq \frac{1}{N^2}$. Esto nos garantiza que $g(x)\leq s(x)$, donde $s$ es la función «escalonada»: \begin{equation*} s(x)= \begin{cases} 1 & \text{si } x [-1,1) \\ \frac{1}{k^2} & \text{si } x \in [k,k+1),[-(k+1),k) \end{cases} \end{equation*} Invocando el teorema de la convergencia monótona para calcular $\int s \ \mathrm{d}\lambda$ concluimos:

\begin{align*}
\int g \ \mathrm{d}\lambda &\leq \int s \ \mathrm{d}\lambda \\
&= 1\cdot\lambda([-1,1))+\sum_{k=1}^{\infty}\frac{1}{k^2}\cdot\lambda([k,k+1))+\sum_{k=1}^{\infty}\frac{1}{k^2}\cdot\lambda([-(k+1),-k)) \\
&= 2+2\sum_{k=1}^{\infty}\frac{1}{k^2} \\
&< \infty.
\end{align*}

Entonces $g$ satisface las condiciones del teorema de la convergencia dominada y los cálculos en (2) son válidos. Concluimos $$\lim_{k\to \infty} \int_{\mathbb{R}}\left(1+ \frac{x^2}{k} \right)^{-k}\sin\left( \frac{x}{k} \right) \ \mathrm{d}x=0.$$

$\triangle$

Más adelante…

Definiremos el concepto de casi donde sea, un concepto de gran utilidad en la teoría de integración. Daremos versiones más generales de los teoremas de convergencia que hemos probado hasta ahora aprovechando esta idea.

Tarea moral

• Para cada $k\in \mathbb{N}$, definamos $f_k(x)=\frac{k\sin(x)}{1+k^2x^2}$. Encuentra $$\lim_{k\to \infty}\int f_k(x) \ \mathrm{d}x.$$ [SUGERENCIA: Encuentra el límite puntual de $\{ f_k\}_{k=1}^{\infty}$. Domina la sucesión por un múltiplo de $\frac{1}{1+x^2}\in L^1(\mathbb{R})$].
• Sea $t_k=\chi_{[k,k+1]}$ para cada $k=1,2,\dots$ Verifica que $$\lim_{k\to \infty}\int t_k \ \mathrm{d}\lambda=1\neq 0=\int \left( \lim_{k\to \infty} t_k\right) \ \mathrm{d}\lambda.$$ ¿Porqué no aplica el teorema de la convergencia dominada?
• Sea $f\in L^1(\mathbb{R}^n)$. Para cada $k\in \mathbb{N}$, definamos $A_k=\{x \ : \ |f(x)|\leq k \}$ y $f_k=f\cdot \chi_{A_k}$. Demuestra que $$\lim_{k\to \infty}\int f_k \ \mathrm{d}\lambda=\int f \mathrm{d}\lambda.$$
• (Condiciones para intercambiar límites y derivadas con integrales). Sea $f:\mathbb{R}^n\times [a,b]\to [-\infty,\infty]$ ($a<b$) tal que para cada $t\in [a,b]$ la función $f_t:\mathbb{R}^n\to [-\infty, \infty]$, dada por $f_t(x)=f(x,t)$, es integrable. Sea $F(t)=\int_{\mathbb{R}^n}f_t \ \mathrm{d}\lambda=\int_{\mathbb{R}^n}f(x,t) \ \mathrm{d}x$.
  • Supón que existe $g\in L^1(\mathbb{R}^n)$ tal que $|f(x,t)|\leq g(x)$ para todo $x,t$ y que $\lim_{t\to t_0}f(x,t)=f(x,t_0)$ para todo $x\in \mathbb{R}^n$. Prueba que $$\lim_{t\to t_0}F(t)=F(t_0).$$ En particular, si $f(x,\cdot)$ es continua para cada $x$, entonces $F$ es continua sobre $[a,b]$.
  • Supón que $\frac{\partial f}{\partial t}$ existe y además podemos encontrar $g\in L^1(\mathbb{R}^n)$ tal que $\left |\frac{\partial f}{\partial t}(x,t) \right|\leq g(x)$ para todo $(x,t)$. Prueba que $F$ es diferenciable y $$F'(x)=\int \frac{\partial f}{\partial t}(x,t) \ \mathrm{d}x.$$ [SUGERENCIA: Utiliza el teorema del valor medio para acotar el cociente de diferencias $\left| \frac{f(x,t+h)-f(x,t)}{h}\right|\leq g(x)$. Aplica el teorema de la convergencia dominada haciendo tender $h\to 0$].
• (Generalización del teorema de la convergencia dominada). Sea $f_1,f_2,\dots$ una sucesión de funciones medibles definidas sobre $\mathbb{R}^n$ tales que $$\lim_{k\to \infty}f_k(x)=f(x)$$ Existe para cada $x\in \mathbb{R}^n$. Supongamos que existen funciones $g_1,g_2,\dots \in L^1(\mathbb{R}^n)$ tales que
  • $|f_k(x)|\leq g_k(x)$ para todo $x\in \mathbb{R}^n$.
  • $\lim_{k\to \infty}g_k(x)=g(x)$ para todo $x\in \mathbb{R}^n$, con $g\in L^1(\mathbb{R}^n)$.
  • $\lim_{k\to \infty}\int g_k \ \mathrm{d}\lambda=\int g \ \mathrm{d}\lambda.$
    Demuestra que $$\lim_{k\to \infty}\int f_k \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda.$$ [SUGERENCIA: Imita la demostración del teorema de la convergencia dominada].

Introducción

Hasta ahora, sólo hemos definido la integral para funciones medibles no negativas. En esta entrada veremos que la definición se puede extender a funciones medibles más generales (no necesariamente $\geq 0$) heredando muchas de sus propiedades. Definiremos también el concepto de integrabilidad (o función $L^1$) que será una hipótesis esencial en muchos de nuestros desarrollos más adelante.

Definición. Sea $f:\mathbb{R}^n\to [-\infty,\infty]$ una función medible, con parte positiva y negativa $f_+$ y $f_-$ respectivamente. Definimos la integral de $f$ como

$$\int f \ \mathrm{d} \lambda=\int f_+ \ \mathrm{d} \lambda-\int f_- \ \mathrm{d} \lambda.$$

Siempre que este número esté bien definido.

Definición. Si $\int f_+ \ \mathrm{d} \lambda$ y $\int f_- \ \mathrm{d} \lambda$ son ambas finitas, entonces decimos que $f$ es integrable.

Notación. Denotaremos a la clase de funciones integrables como $L^1(\mathbb{R}^n,\mathcal{L},\lambda)$, $L^1(\mathbb{R}^n)$ , o simplemente $L^1$.

Observaciones.

• La definición tiene sentido (siempre que $\int f_+ \ \mathrm{d} \lambda-\int f_- \ \mathrm{d} \lambda$ exista), pues si $f$ es medible entonces $f_+$ y $f_-$ son medibles no negativas por lo que admiten integrales bien definidas.
• Si $f\geq 0$, la nueva definición es consistente con la definición de integral para funciones medibles no negativas, pues en este caso $f=f_+$ y $f_-=0$.
• A diferencia de las funciones no negativas, no todas las funciones medibles admiten una integral. Si $\int f_+ \ \mathrm{d}\lambda=\int f_- \ \mathrm{d}\lambda=\infty$, $\int f \ \mathrm{d}\lambda$ no está bien definida.
• Si $f\in L^1(\mathbb{R}^n)$, entonces $\int f_+ \ \mathrm{d} \lambda-\int f_- \ \mathrm{d} \lambda$ es un número real. Enfocaremos nuestro análisis principalmente en las funciones en $L^1$ pues es un espacio más manejable pero al mismo tiempo lo suficientemente general.
• Más adelante le daremos un significado ligeramente distinto al conjunto $L^1(\mathbb{R}^n)$. De momento es conveniente pensar que $f\in L^1$ es un atajo notacional para decir que $f$ es integrable.

Veamos primero un par de Lemas que facilitarán nuestro estudio de las funciones integrables.

Lema. Si $f:\mathbb{R}^n\to [0,\infty]$ es una función medible, no negativa y con integral finita $0\leq \int f \ \mathrm{d} \lambda<\infty$, entonces $I=\{ x\in \mathbb{R}^n \ | \ f(x)=\infty\}$ es de medida cero.

Demostración. Supongamos por el contrario que $\lambda(I)>0$. Consideremos la sucesión de funciones simples: $$s_k=k\chi_I \ \ \ \ \forall k\in \mathbb{R}^n.$$
Claramente $s_k\leq f$ para toda $k$, de donde $$\int f \ \mathrm{d} \lambda\geq \int s_k \ \mathrm{d} \lambda=k\lambda(I).$$
Como $k\lambda(I)\longrightarrow \infty$ cuando $k\longrightarrow \infty$, la única posibilidad es $$\int f \ \mathrm{d} \lambda=\infty.$$ Lo cual es una contradicción.

$\square$

Proposición (desigualdad del triángulo). Si $f$ es una función medible y con integral bien definida, entonces $$\left| \int f \ \mathrm{d} \lambda \right|\leq \int |f| \ \mathrm{d} \lambda.$$ Además $f\in L^1$ $\iff$ $|f|\in L^1$.

Demostración. Notemos que $|f|=f_++f_-$. Como $f_+$ y $f_-$ son medibles no negativas, se sigue por aditividad: $$\int |f| \ \mathrm{d} \lambda=\int f_+ \ \mathrm{d} \lambda+\int f_- \ \mathrm{d} \lambda.$$
Evidentemente $\int f_+ \ \mathrm{d} \lambda\leq \int f_+ \ \mathrm{d} \lambda$ y $-\int f_- \ \mathrm{d} \lambda\leq \int f_- \ \mathrm{d} \lambda$, por lo que $$\int f \ \mathrm{d} \lambda=\int f_+ \ \mathrm{d} \lambda-\int f_- \ \mathrm{d} \lambda\leq \int f_+ \ \mathrm{d} \lambda+\int f_- \ \mathrm{d} \lambda=\int |f| \ \mathrm{d} \lambda.$$

Análogamente $$-\int f \ \mathrm{d} \lambda=\int f_- \ \mathrm{d} \lambda-\int f_+ \ \mathrm{d} \lambda\leq \int f_+ \ \mathrm{d} \lambda+\int f_- \ \mathrm{d} \lambda=\int |f| \ \mathrm{d} \lambda.$$

Por lo que $$\left| \int f \ \mathrm{d} \lambda \right|\leq \int |f| \ \mathrm{d} \lambda.$$

Si $f\in L^1$ $$\implies \ \int f_+ \ \mathrm{d} \lambda,\int f_- \ \mathrm{d} \lambda<\infty$$ $$\implies \ \int |f| \ \mathrm{d} \lambda=\int f_+ \ \mathrm{d} \lambda+\int f_- \ \mathrm{d} \lambda<\infty.$$ De modo que $|f|\in L^1$.

Inversamente, supongamos que $|f|\in L^1$. Como $f_+,f_-\leq |f|$ $$\implies \ \int f_+ \ \mathrm{d} \lambda, \ \int f_- \ \mathrm{d} \lambda\leq \int |f| \ \mathrm{d} \lambda < \infty$$ Por lo que $f\in L^1$.

$\square$

Proposición (Linealidad de la Integral). Supongamos que $f,g\in L^1$ y $a, b\in \mathbb{R}$. Entonces $af+bg\in L^1$ con $$\int (af+bg) \ \mathrm{d}\lambda=a\int f \ \mathrm{d}\lambda+b\int g \ \mathrm{d}\lambda.$$

Observación. Hay un un detalle en ésta proposición: es posible que $af+bg$ no esté definida en todo $\mathbb{R}^n$ (piensa por ejemplo que $f(0)=g(0)=\infty$ $\implies$ $(f-g)(0)$ no está definida). Los puntos que «pueden dar problemas» son aquellos en los que $f$ ó $g$ valen $\pm \infty$. Por el lema anterior, éste conjunto es de medida cero así que $af+bg$ está bien definida salvo quizá un conjunto de medida cero. Más adelante veremos que a la hora de integrar podemos «ignorar» los conjuntos de medida cero, es decir, podemos redefinir $f$ y $g$ en cualquier conjunto de medida cero sin afectar el valor de su integral. Por esta razón podemos suponer sin mayor problema que $f,g$ son finitas en todo $\mathbb{R}^n$.

Demostración. Basta probar por separado: $$\int af \ \mathrm{d}\lambda=a\int f \ \mathrm{d}\lambda,$$ $$\int (f+g) \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda+\int g \ \mathrm{d}\lambda.$$

Veamos la primera parte. Podemos distinguir dos casos:

• Si $a\geq 0$, tenemos $(af)_+=af_+$ y $(af)_-=af_-$. Luego
  \begin{align*}
  \int af \ \mathrm{d}\lambda &= \int af_+ \ \mathrm{d}\lambda – \int af_- \ \mathrm{d}\lambda \\
  &= a \int f_+ \ \mathrm{d}\lambda – a \int f_- \ \mathrm{d}\lambda \\
  &= a\left( \int f_+ \ \mathrm{d}\lambda-\int f_- \ \mathrm{d}\lambda \right) \\
  &= a \int f \ \mathrm{d}\lambda
  \end{align*} En la segunda igualdad usamos la proposición para el caso $f\geq 0$ que ya probamos anteriormente.
• Similarmente, cuando $a<0$, $(af)_+=(-a)f_-$ y $(af)_-=(-a)f_+$, luego
  \begin{align*}
  \int af \ \mathrm{d}\lambda &= \int (-a)f_- \ \mathrm{d}\lambda – \int (-a)f_+ \ \mathrm{d}\lambda \\
  &= (-a) \int f_- \ \mathrm{d}\lambda + a \int f_+ \ \mathrm{d}\lambda \\
  &= a\left( \int f_+ \ \mathrm{d}\lambda-\int f_- \ \mathrm{d}\lambda \right) \\
  &= a \int f \ \mathrm{d}\lambda.
  \end{align*}

Veamos ahora la segunda parte. Sea $h=f+g$. Entonces $|h|\leq |f|+|g|$ $\implies$ $\int |h| \ \mathrm{d}\lambda\leq \int |f| \ \mathrm{d}\lambda+\int |g| \ \mathrm{d}\lambda<\infty$ $\implies$ $|h|\in L^1$ $\implies$ $h\in L^1$ (desigualdad del triángulo).

Ahora, como podemos escribir: $$h_+-h_-=h=f+g=(f_+-f_-)+(g_+-g_-)$$
$$\implies \ h_++f_-+g_-=h_-+f_++g_+$$

Integrando y usando la proposición para funciones no negativas (que ya probamos)
$$\implies \int h_+ \ \mathrm{d}\lambda+\int f_- \ \mathrm{d}\lambda+\int g_- \ \mathrm{d}\lambda=\int h_- \ \mathrm{d}\lambda+ \int f_+ \ \mathrm{d}\lambda+\int g_+ \ \mathrm{d}\lambda.$$

Reordenando los términos y usando la definición concluimos:
$$\int (f+g) \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda+\int g \ \mathrm{d}\lambda.$$

$\square$

Corolario (Monotonía de la integral). Sean $f,g\in L^1(\mathbb{R}^n)$ con $f\leq g$. Entonces $$\int f \ \mathrm{d}\lambda \leq \int g \ \mathrm{d}\lambda.$$

Demostración. Notemos que $g-f\geq 0$. Por el teorema anterior, sabemos que $g-f\in L^1(\mathbb{R}^n)$ y además:

$$0\leq \int (g-f) \ \mathrm{d}\lambda=\int g \ \mathrm{d}\lambda-\int f \ \mathrm{d}\lambda$$
$$\implies \int f \ \mathrm{d}\lambda\leq \int g \ \mathrm{d}\lambda.$$

$\square$

Más adelante…

Enunciaremos y probaremos otro de los teoremas más importantes de teoría de integración: El Teorema de la Convergencia Dominada. Al igual que el Teorema de la convergencia Monótona, éste es un resultado de «intercambio de límites con integrales», pero es aplicable incluso cuando las funciones no son $\geq 0$.

Tarea Moral

• Demuestra que si $f:\mathbb{R}^n\to [-\infty,\infty]$ es integrable, entonces para cualquier $M>0$$$\lambda(\{ x \ | \ |f(x)|>M\})<\infty.$$
• Demuestra que si $f:\mathbb{R}^n\to [-\infty,\infty]$ es integrable, entonces $$\lambda(\{ x \ | \ f(x)=\pm \infty\})=0.$$
• Prueba que la función $f(x)=\frac{1}{x}$ si $x\neq 0$; $f(0)=0$ NO es integrable. [SUGERENCIA: Compara $f_+$ con alguna función escalonada cuya integral sea una suma armónica $\sum_{k=1}^{\infty}\frac{1}{k}=\infty$].
• Sea $f:\mathbb{R}\to [-\infty,\infty]$ una función medible tal que:
  • f es acotada en el intervalo $[-1,1]$.
  • $|f(x)|\leq \frac{1}{k^2}$ si $|x|\leq k$.
    Demuestra que $f\in L^1(\mathbb{R})$.
• (Desigualdad de Chebyshev). Sea $f\in L^1(\mathbb{R}^n)$. Demuestra que $$\lambda(\{ x \ | \ |f(x)|\geq \alpha\})\leq \frac{1}{\alpha}\int |f| \ \mathrm{d}\lambda.$$

Introducción

Contrario a lo que la intuición podría sugerir, en general los límites no conmutan con integrales. A pesar de esto, sí que podemos dar un estimado bastante útil a la hora de comparar límites de integrales: El Lema de Fatou.

Las hipótesis del Teorema de la Convergencia Monótona no se pueden relajar

En general, no siempre podemos intercambiar límites con integrales. Veamos un ejemplo.

Ejemplo. Para cada $k\in \mathbb{N}$, definamos $$g_k=\chi_{[k-1,k]}.$$ Observa que $\{ g_k \}_{k=1}^{\infty}$ es una sucesión de funciones simples, medibles y no negativas. Además, para cualquier $x\in \mathbb{R}$, podemos encontrar un $N\in \mathbb{N}$ suficientemente grande tal que $x<N-1$, es decir, $x\notin [k-1,k]$ para $k\geq N$. Esto garantiza que la sucesión $g_k(x)$ es eventualmente $0$. Concluimos que $$\lim_{k\to \infty} g_k=0.$$
Sin embargo, para cualquier $k$: $$\int g_k \ \mathrm{d}\lambda = 1\cdot \lambda([k-1,k])=1. $$
De modo que $$\int \left( \lim_{k\to \infty} g_k \right) \ \mathrm{d}\lambda=0\neq 1=\lim_{k\to \infty} \int g_k \ \mathrm{d}\lambda.$$

$\triangle$

Destacamos que la hipótesis de que la sucesión de funciones sea creciente es esencial para poder intercambiar límites con integrales.

El Lema de Fatou

Lema (de Fatou). Sean $f_1, f_2, f_3\dots$ funciones medibles y no negativas. Entonces:

$$\int \left( \liminf_{k\to \infty} f_k \right) \ \mathrm{d}\lambda \leq \liminf_{k\to \infty} \int f_k \ \mathrm{d}\lambda.$$

Demostración. Para cada $k\in \mathbb{N}$, definamos: $$g_k=\inf \{ f_k, f_{k+1}, f_{k+2}, \dots \}.$$

Observa que $\{ g_k \}_{k=1}^{\infty}$ es una sucesión creciente de funciones medibles no negativas. Además $g_k\leq f_k$ para todo $k$, de donde $\int g_k \ \mathrm{d}\lambda\leq \int f_k \ \mathrm{d}\lambda$.

Luego, invocando el teorema de la convergencia monótona:

\begin{align*}
\int \left( \liminf_{k\to \infty} f_k \right) \ \mathrm{d}\lambda &= \int \left( \lim_{k\to \infty} \inf_{m\geq k} f_m \right) \ \mathrm{d}\lambda \\
&= \int \left( \lim_{k\to \infty} g_k \right) \ \mathrm{d}\lambda \\
&= \lim_{k\to \infty} \int g_k \ \mathrm{d}\lambda \\
&\leq \liminf_{k\to \infty} \int f_k \ \mathrm{d}\lambda.
\end{align*}

$\square$

Algunas consideraciones sobre el Lema de Fatou

Observación. En general también es cierto que $$\int \liminf_{k\to \infty}f_k \ \mathrm{d}\lambda \leq \limsup_{k\to \infty} \int f_k \ \mathrm{d}\lambda$$ Simplemente porque $\liminf \int f_k\leq \limsup \int f_k$, aunque este estimado es más débil.

Ejemplo. La igualdad en el teorema de Fatou puede ser estricta. Consideremos dos sucesiones $a_k$ y $b_k$ tales que $$a_k\longrightarrow \frac{1}{2}$$ Y $$b_k\longrightarrow \frac{1}{2}.$$
Con $0=a_0<a_1<a_2<\dots$ y $1=b_0>b_1>b_2>\dots$

Definamos $$s_k=\frac{\chi_{[a_k,b_k]}}{b_k-a_k}.$$

\begin{equation*}
\implies (\liminf_{k\to \infty} s_k)(x)=
\begin{cases}
0 & \text{si } x \neq \frac{1}{2} \\
\frac{1}{b_0-a_0} & \text{si } x = \frac{1}{2}.
\end{cases}
\end{equation*}

$$\implies \int \liminf_{k\to \infty} s_k \ \mathrm{d}\lambda= 1 \cdot \lambda\left(\left\{ \frac{1}{2} \right\}\right)=0.$$

Pero $$\int s_k \ \mathrm{d}\lambda = \frac{1}{b_k-a_k}\lambda([a_k,b_k])=1.$$ Para todo $k$. Así que en este caso: $$\int \liminf_{k\to \infty} s_k \ \mathrm{d}\lambda=0<1 = \liminf \int s_k \ \mathrm{d}\lambda.$$

$\triangle$

Ejemplo. No hay una versión del Lema de Fatou con $\limsup$ en lugar de $\liminf$ (a menos de que pidamos más condiciones).

• En general $$\int \limsup_{k\to \infty} f_k \ \mathrm{d}\lambda \ngeq \limsup_{k\to \infty} \int f_k \ \mathrm{d}\lambda.$$
  Consideremos $s_k$ como en el ejemplo anterior: $$s_k=\frac{\chi_{[a_k,b_k]}}{b_k-a_k}.$$
  Ahora tenemos
  \begin{equation*}
  \limsup_{k\to \infty} s_k(x)=
  \begin{cases}
  0 & \text{si } x \neq \frac{1}{2} \\
  \infty & \text{si } x = \frac{1}{2}.
  \end{cases}
  \end{equation*}
  $$\implies \int \limsup_{k\to \infty} s_k \ \mathrm{d}\lambda = \infty \cdot \lambda\left(\left\{ \frac{1}{2} \right\}\right)=0.$$
  Pero $$\limsup_{k\to \infty} \int s_k \ \mathrm{d}\lambda=1.$$
• Tampoco se cumple siempre que $$\int \limsup_{k\to \infty} f_k \ \mathrm{d}\lambda \leq \limsup_{k\to \infty} \int f_k \ \mathrm{d}\lambda.$$
  Para ello consideremos una sucesión de subconjuntos medibles $A_k \subseteq \mathbb{R}$ con $\lambda(A_k)=1$ y tales que el conjunto $$S_x=\{k\in \mathbb{N} \ | \ x\in A_k \}$$ Sea infinito para todo $x\in \mathbb{R}$.
  Podemos construir una sucesión de tales $A_k$ de la siguiente manera: Tomamos $\{ r_k \}_{k=1}^{\infty}$ una enumeración de $\mathbb{Q}$ y definimos $A_k$ como el intervalo de longitud 1 centrado en $r_k$ (no importa si el intervalo es abierto o cerrado).
  Ahora, sea $$s_k=\chi_{A_k}.$$ Entonces, para cada $k\in \mathbb{N}$ $$\int s_k \ \mathrm{d}\lambda=\lambda(A_k)=1$$ De donde $$ \limsup_{k\to \infty} \int s_k \ \mathrm{d}\lambda =1. $$
  Por otro lado, $$\limsup_{k\to \infty}s_k= \chi_{\mathbb{R}}\equiv1$$ $$\implies \int \limsup_{k\to \infty} s_k \ \mathrm{d}\lambda =\lambda(\mathbb{R})=\infty.$$

$\triangle$

A pesar de lo anterior, sí que podemos dar una versión «dual» del Lema de Fatou si asumimos algunas condiciones adicionales. Para la demostración del siguiente resultado, requerimos definir la integral de una función negativa: Si $f\leq 0$ es medible, definimos provisionalmente $\int f \ \mathrm{d}\lambda:=-\int (-f) \ \mathrm{d}\lambda$. Asumiremos también que «la integral abre restas», es decir, que $\int (f-g) \ \mathrm{d}\lambda=\int f \ \mathrm{d}\lambda-\int g \ \mathrm{d}\lambda$. En la siguiente entrada probaremos estas y muchas otras propiedades de la integral de funciones no necesariamente $\geq 0$.

Lema (dual de Fatou). Sean $f_1,f_2,\dots$ funciones no negativas y medibles. Supongamos además que existe una función medible $f$ tal que

1. $f_k\leq f$ para todo $k\in \mathbb{N}$.
2. $\int f \ \mathrm{d}\lambda <\infty$.

Entonces, $$\limsup_{k\to \infty} \int f_k \ \mathrm{d}\lambda \leq \int \limsup_{k\to \infty} f_k \ \mathrm{d}\lambda.$$

Demostración. Consideremos $$g_k:=f-f_k.$$ Luego:

• $g_k \geq 0$ (por 1.)
• $g_k$ es Lebesgue medible (al ser combinación lineal de funciones medibles).

Entonces, el Lema de Fatou implica que:
$$\int \liminf_{k\to \infty} g_k \ \mathrm{d}\lambda\leq \liminf_{k\to \infty} \int g_k \ \mathrm{d}\lambda.$$ Es decir $$\int \liminf_{k\to \infty} (f-f_k) \ \mathrm{d}\lambda\leq \liminf_{k\to \infty} \left( \int f \ \mathrm{d}\lambda – \int f_k \ \mathrm{d}\lambda \right).$$
$$\implies \int f \ \mathrm{d}\lambda+\int \liminf_{k\to \infty} (-f_k) \ \mathrm{d}\lambda\leq \int f \ \mathrm{d}\lambda +\liminf_{k\to \infty} \left( – \int f_k \ \mathrm{d}\lambda \right).$$
Restando $\int f \ \mathrm{d}\lambda<\infty$ de ambos lados y usando que $\liminf -a_k=-\limsup a_k$ concluimos:
$$\limsup_{k\to \infty} \int f_k \ \mathrm{d}\lambda \leq \int \limsup_{k\to \infty} f_k \ \mathrm{d}\lambda.$$

$\square$

Más adelante…

Definiremos la integral para funciones medibles generales (no necesariamente $\geq 0$) y el concepto de función integrable (ó $L^1$). Veremos varias de sus propiedades, muchas análogas a las que hemos visto hasta ahora, aunque también algunas nuevas.

Tarea moral

• Sea $f_k=\chi_{[0,\frac{1}{k}]}$ para cada $k\in \mathbb{N}$. Calcula $\int (\liminf f_k) \ \mathrm{d}\lambda$ y $\liminf \int f_k \ \mathrm{d}\lambda$. ¿Se satisface el Lema de Fatou? ¿La desigualdad es estricta?
• Sea $f_k=\chi_{[k,k+1]}$ para cada $k\in \mathbb{N}$. Calcula $\int (\liminf f_k) \ \mathrm{d}\lambda$ y $\liminf \int f_k \ \mathrm{d}\lambda$. ¿Se satisface el Lema de Fatou? ¿La desigualdad es estricta?
• Sean $f_1,f_2,\dots$ funciones medibles definidas sobre $\mathbb{R}^n$ tales que $f_k\longrightarrow f$ puntualmente. Sea $g:\mathbb{R}\to [0,\infty)$ una función continua y no negativa. Prueba que $$\int g\circ f \ \mathrm{d}\lambda \leq \liminf_{k\to \infty} \int g\circ f_k \ \mathrm{d}\lambda.$$