Ejemplo 1
Sea $f : \mathbb{R}^2 \rightarrow \mathbb{R}$
$f(x, y) = \left\{ \begin{array} \dfrac{}\dfrac{2xy}{x^2 + y^2} & si & (x, y) \neq (0, 0) \\ \\ 0 & si & (x, y) = (0, 0) \end{array} \right.$
Observamos que:
(*) Existen las derivadas parciales en todos los puntos $(x, y) \in \mathbb{R}^2$.
(*) No es continua, veamos porque:
$\Big\{ \Big( \dfrac{1}{n}, \dfrac{1}{n} \Big) \Big\} \rightarrow (0, 0)$ pero $\Big\{ f \Big( \dfrac{1}{n}, \dfrac{1}{n} \Big) \Big\} \nrightarrow f (0, 0) = 0$,
ya que $ f \Big( \dfrac{1}{n}, \dfrac{1}{n} \Big) = \dfrac{2 \frac{1}{n} \frac{1}{n}}{\frac{1}{n^2} + \frac{1}{n^2}} = \dfrac{ \frac{2}{n^2}}{ \frac{2}{n^2}} = 1 \rightarrow 1$
(*) Tampoco es diferenciable.
En la siguiente imagen puedes observar la gráfica de la función descrita en este ejemplo.
https://www.geogebra.org/classic/rkapmzg2
${}$
Ejemplo 2
Sea $f : \mathbb{R}^2 \rightarrow \mathbb{R}$
$ f (x, y) = \left\{ \begin{array} \\ y^2 \sin{ \Bigg( \dfrac{1}{y} \Bigg)} & si & y \neq 0 \\ \\ \\ 0 & si & y = 0 \end{array} \right. $
Observemos que:
(*) En el punto $(0, 0)$ es diferenciable.
(*) $ \dfrac{\partial f}{\partial x} (0, 0) = 0 =\dfrac{\partial f}{\partial y} (0, 0)$
El plano tangente en el origen es el plano $XY$ pero las derivadas parciales NO son continuas.
En particular $\dfrac{ \partial f}{\partial y} (x, y).$
En la siguiente imagen puedes observar la gráfica de la función descrita en este ejemplo.
https://www.geogebra.org/classic/ksdzu5qx
${}$
Ejemplo 3
Sea $f : \mathbb{R}^2 \rightarrow \mathbb{R}$
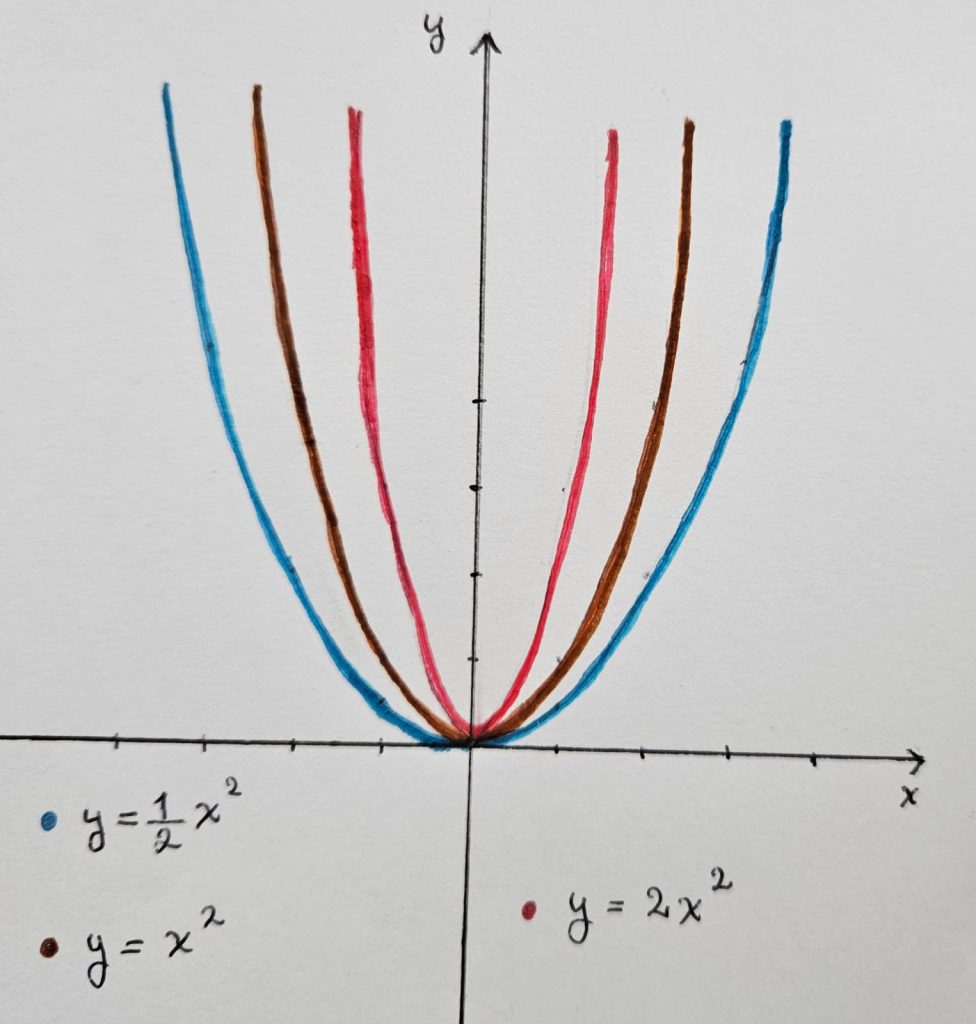
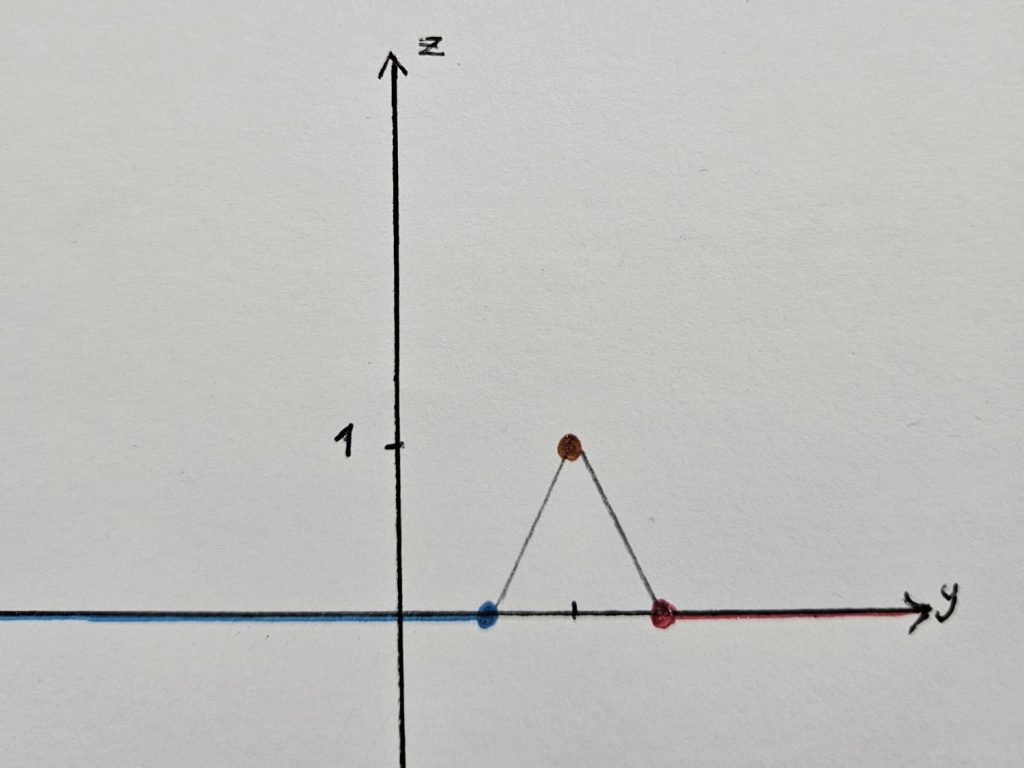
$ f (x, y) = \left\{ \begin{array}\\1 & si & (x, y) \neq (0, 0) \text{ está en la parábola } \, y = x^2 \\ \\ 0 & si & (x, y) \neq (0, 0) \text{ está en la parábola } y = \frac{1}{2} x^2 \text{ o más abajo} \\ \\ 0 & si & (x, y) = (0, 0) \text{ está en la parábola } y = 2x^2 \text{ o más arriba } \\ 0 & si & y = 0 \end{array} \right.$
Corte $x = 0$ vale $0$.
Observamos que:
(*) Es continua en cada corte pero globalmente NO es continua.
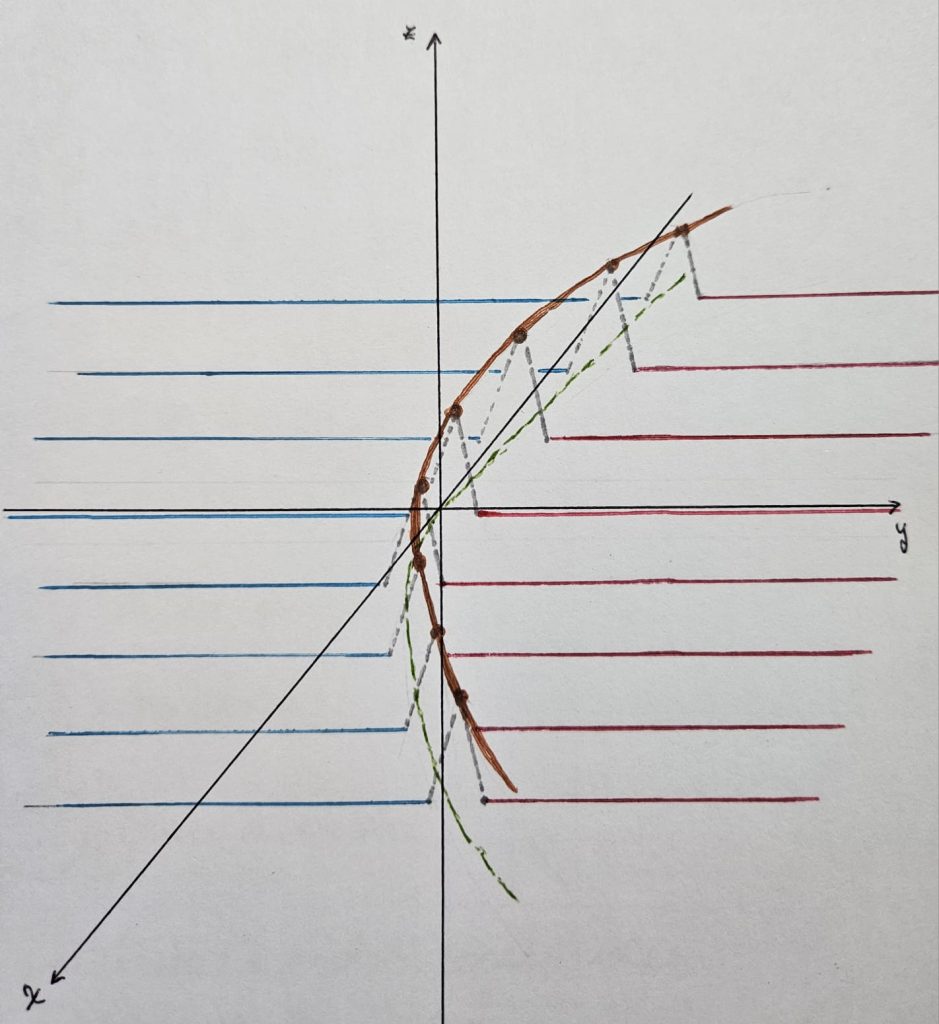
(*) Además en este ejemplo existen todas las derivadas direccionales en el $(0, 0)$.
$$ \forall \, \vec{u} \in \mathbb{R}^2 \; \| \vec{u} \| = 1, \, \exists \, \lim_{t \rightarrow 0} \dfrac{f (t \vec{u} \, – \, f (\vec{0}) }{t}$$
${}$
Al analizar los ejemplos anteriores nos preguntamos, ¿cuándo podemos garantizar la continuidad?
${}$