Además de las coordenadas cartesianas es conveniente conocer otros tipos de coordenadas, como las polares, cilíndricas y esféricas, estas últimas las explicaremos en entradas posteriores; ya que muchas veces es más sencillo de resolver problemas si cambiamos de coordenadas cartesianas a otro tipo según el tipo de función con la que estemos trabajando.

En este primer acercamiento, estudiaremos como realizar la conversión de coordenadas cartesianas a polares y viceversa.

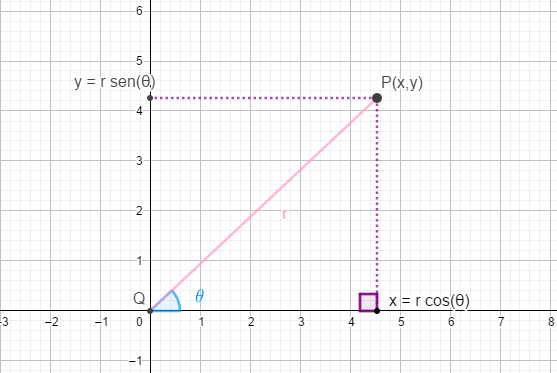
En el dibujo podemos observar que para un punto $P(x,y)$ se tiene un triángulo rectángulo, en esta imagen el triángulo $PXQ$, por lo que usando el Teorema de Pitágoras y las razones trigonométricas correspondientes, tenemos que:

$$x^2+y^2=r^2$$ $$\sin \theta =\frac{y}{r}$$ $$\cos \theta =\frac{x}{r}$$

Entonces, las ecuaciones que nos permiten transformar de coordenadas polares a rectangulares son:

$$x=r\cos (\theta )$$ $$y=r\sin (\theta )$$

$(x,y)$ son las coordenadas cartesianas (o rectangulares) del punto $P$.

$(r,\theta )$ son las coordenadas polares del punto $P$.

* CASO ESPECIAL: para el punto $(0,0)$ en coordenadas cartesianas tenemos que $r=0$ y el ángulo $\theta$ no está definido.

* También es importante especificar un intervalo donde varía el ángulo $\theta$, para evitar situaciones como la que se ejemplifica a continuación.

El punto de coordenadas rectangulares $(1,0)$ puede tener diferentes coordenadas polares, como $(1,0°)$, $(1,360°)$ si el ángulo está dado en grados, o $(1,0)$, $(1,2\pi )$ si el ángulo se mide en radianes.

Por lo que se puede definir a $\theta$ en el intervalo $0<\theta <2\pi$ o en el $-\pi <\theta <\pi$.