Consideremos una población constante distribuida en dos países.
Supongamos que cada año:
- $\frac{1}{4}$ parte de la población que está en $A$ emigra a $B$.
- $\frac{3}{4}$ partes se quedan en $A$.
- $\frac{1}{2}$ parte de la población que está en $B$ emigra hacia $A$.
- $\frac{1}{2}$ parte se quedan en $B$.
$x_n$: la población de $A$
$y_n$: la población de $B$
después de $n$ años
$(x_0, y_0)$ población inicial.
¿Qué pasará cuando pasen muchos años? $$n \longrightarrow \infty$$
¿Se alcanza un equilibrio?
Sistema Dinámico
$x_{n+1}= \frac{3}{4} x_n + \frac{1}{2} y_n$
$y_{n + 1}=\frac{1}{4} x_n + \frac{1}{2} y_n$
\begin{equation*} \begin{pmatrix} x_{n+1} \\ \\ y_{n+1} \end{pmatrix} = \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \\ \frac{1}{4} & \frac{1}{2} \end{pmatrix}\begin{pmatrix} x_n \\ \\ y_n \end{pmatrix} \end{equation*}
$\overrightarrow{x_{n+1}} = A\, \overrightarrow{x_n}$
$\overrightarrow{x_0} \curvearrowright \overrightarrow {x_1} \curvearrowright \overrightarrow{x_2} \curvearrowright \overrightarrow{x_3} \cdots $
De modo que $\overrightarrow{x_1} = A \overrightarrow{x_0} ; \quad \overrightarrow{x_2}= A^2 \, \overrightarrow{x_0}$ en general $$\overrightarrow{x_n} = A^n \, \overrightarrow{x_0}$$
Si $A$ fuera diagonal $\begin{pmatrix} \lambda_1 & 0 \\ \\ 0 & \lambda_2 \end{pmatrix}$ entonces:
$\begin{equation*} A^2 = \begin{pmatrix} \lambda_1^2 & 0 \\ \\ 0 & \lambda_2^2 \end{pmatrix} \end{equation*}$ en general $\begin{equation*} A^n = \begin{pmatrix} \lambda_1^n & 0 \\ \\ 0 & \lambda_2^n \end{pmatrix} \end{equation*}$
Si pensamos en la transformación lineal $$T(\vec{x}) = A\, \vec{x} \hspace{2cm} T: \mathbb{R}^2 \rightarrow \mathbb{R}^2$$
podemos preguntarnos si existe una base $\{\vec{v}, \vec{w} \}$ de $\mathbb{R}^2$ en la cual la matriz asociada a la transformación lineal sea diagonal, es decir, tal que:
$$ \begin{equation}T (\vec{v}) = \lambda \vec{v} \end{equation}$$ $$\begin{equation} T (\vec{w}) = \lambda \vec{w} \end{equation}$$
$\begin{equation*} P = \begin{pmatrix} v_1 & w_1 \\ v_2 & w_2 \end{pmatrix} \end{equation*}$
$\begin{equation*} P\overrightarrow{e_1} = \vec{v} =\begin{pmatrix} v_1 \\ v_2 \end{pmatrix} \end{equation*}$
$\begin{equation*} P\overrightarrow{e_2} = \vec{w} =\begin{pmatrix} w_1 \\ w_2 \end{pmatrix} \end{equation*}$
Decimos que $A$ es diagonalizable si existe $P$ invertible tal que cumpla con la igualdad $A = PDP^{-1}$, para alguna matriz diagonal $D$.
$D = \begin{pmatrix} \lambda && 0 \\ 0 && \mu \end{pmatrix}$
Buscamos un vector $\vec{v}$ con $\vec{v} \neq \vec{0}$ tal que $$A \vec{v} = \lambda \vec{v}$$
Observación: A $\lambda$ se le llama valor propio, eigenvalor, valor característico o autovalor. Y por tanto, $\overrightarrow{v}$ se denomina vector propio, eigenvector, vector característico o autovector.
$A \vec{v} = \lambda \vec{v}$
$A \vec{v} = \lambda I \vec{v}$
$A\vec{v} – \lambda I \vec{v} = \vec{0}$
$(A – \lambda I) \vec{v} = \vec{0}$
$\vec{0}$ es una solución, si queremos que exista otra solución (solución no única), entonces $det (A – \lambda I) = 0$ es la ecuación que determina a los valores propios $\lambda$.
Entonces para nuestro problema
$\begin{equation*} \begin{vmatrix} A – \lambda I \end{vmatrix} = \begin{vmatrix} \frac{3}{4} – \lambda & \frac{1}{2} \\ \\ \frac{1}{4} & \frac{1}{2} \, – \, \lambda \end{vmatrix} = 0 \end{equation*}$
$\left( \frac{3}{4} \, – \, \lambda \right) \left( \frac{1}{2} \, – \, \lambda \right) \, – \, \frac{1}{4} \frac{1}{2} = 0$
$\lambda^2 – \frac{3}{4} \lambda \, – \, \frac{1}{2} \lambda + \frac{3}{8} \, – \, \frac{1}{8} = 0$
$\lambda^2 – \frac{5}{4} \lambda + \frac{1}{4} = 0$
Resolviendo la ecuación de segundo grado se obtienen los valores para $\lambda$ $$\lambda_1 = 1$$ $$\lambda_2 = \frac{1}{4}$$
Entonces la matriz $\begin{equation*}A = \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2}\end{pmatrix} \end{equation*}$ tiene dos valores propios $\lambda_1 = 1$ y $\lambda_2 = \frac{1}{4}$.
Buscamos un vector propio $\vec{v} = (x, y)$ asociado a $\lambda_1 = 1$ tal que cumpla la ecuación $A \vec{v} = \lambda \vec{v}$ como $\lambda_1 = 1$ entonces se tiene la ecuación $A \vec{v} = \vec{v}$
$$\begin{equation*} \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2}\end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} \end{equation*}$$
$$\begin{eqnarray*} \left\{ \frac{3}{4} x + \frac{1}{2} y = x \atop \frac{1}{4} x + \frac{1}{2} y = y \right.\end{eqnarray*}$$
Despejando $y$ de la primera ecuación obtenemos $$\frac{1}{2} y = x – \frac{3}{4} x$$ $$\frac{1}{2} y = \frac{1}{4}x$$ $$y = \frac{1}{2} x$$
El vector $\overrightarrow{v} =\begin{pmatrix} 2 \\ 1 \end{pmatrix}$ cumple las condiciones, es un vector propio asociado a $\lambda_1 = 1$
De manera análoga, buscamos el vector asociado a $\lambda_2 = \frac{1}{4}$.
Si $\lambda_2 = \frac{1}{4}$ entonces $A \vec{w} = \frac{1}{4} \vec{w}$
$$\begin{equation*} \begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2}\end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \frac{1}{4} \begin{pmatrix} x \\ y \end{pmatrix} \end{equation*}$$
$$\begin{eqnarray*} \left\{ \frac{3}{4} x + \frac{1}{2} y = \frac{1}{4}x \atop \frac{1}{4} x + \frac{1}{2} y = \frac{1}{4}y \right.\end{eqnarray*}$$
Despejando $y$ de la primera ecuación obtenemos $$\frac{1}{2} y = \frac{1}{4}x – \frac{3}{4} x$$ $$\frac{1}{2} y = \frac{-2}{4}x$$ $$\frac{1}{2}y = \frac{-1}{2} x$$ $$y = -x$$
El vector $\vec{w} =\begin{pmatrix} 1 \\ -1 \end{pmatrix}$ cumple las condiciones, es un vector propio asociado a $\lambda_2 = \frac{1}{4}$.
$$\begin{equation*} A=\begin{pmatrix} \frac{3}{4} & \frac{1}{2} \\ \frac{1}{4} & \frac{1}{2}\end{pmatrix} = PDP^{-1} \end{equation*}$$
$\begin{equation*} P=\begin{pmatrix} 2 & 1 \\ 1 & -1\end{pmatrix} \end{equation*}$ $\hspace{1cm}$ $\begin{eqnarray*} \left. P \overrightarrow{e_1} = \vec{v} \atop P \overrightarrow{e_2} = \vec{w} \right. \end{eqnarray*}$
$\begin{eqnarray*} A \vec{v} = \vec{v} \\ A \vec{w} = \frac{1}{4} \vec{w} \end{eqnarray*}$
entonces $\begin{equation*} D = \begin{pmatrix} 1 & 0 \\ 0 & \frac{1}{4} \end{pmatrix} \end{equation*}$
Luego
$\begin{eqnarray*} A^n = P D^n P^{-1} \\ D^n = \begin{pmatrix} 1 & 0 \\ 0 & {\frac{1}{4}}^n \end{pmatrix} \end{eqnarray*}$
cuando $n \longrightarrow \infty$ se tiene que $D \longrightarrow \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}$
Entonces $A^n \overrightarrow{x_0} \longrightarrow P \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} P^{-1} \overrightarrow{x_0}$
Recordemos que $\{ \vec{v}, \vec{w} \}$ son base.
Entonces $$\overrightarrow{x_0} = a \vec{v} + b \vec{w}$$
multiplicando por $A$ $$A \overrightarrow{x_0} = A \left( a \vec{v} + b \vec{w} \right)$$
$$A \overrightarrow{x_0} = A a \vec{v} + A b \vec{w}$$
$$A^n \overrightarrow{x_0} = a A^n \vec{v} + b A^n \vec{w}$$
$$A^n \overrightarrow{x_0} = a \vec{v} + b \frac{1}{4^n} \vec{w}$$
De modo que cuando $n \longrightarrow \infty$ se tiene que $\frac{1}{4^n} \longrightarrow \vec{0}$ y por lo tanto $$A^n \overrightarrow{x_0} \longrightarrow a \vec{v}$$
Regresando al problema inicial, si $(x_0, y_0) = (100, 20)$ por lo que calculamos anteriormente:
$$(100, 20) = a (2, 1) + b (1, -1)$$ $$(100, 20) = (2a + b, a \, – \, b)$$
De donde se obtiene el sistema
$$ \left \{ 100 = 2a + b \atop 20 = a \, – \, b \right. $$
Sumando ambas expresiones, obtenemos $120 = 3a$ por lo que $a = 40$; y sustituyendo en la segunda ecuación del sistema al valor de $a$ se tiene que $b = 40 -20$ por lo que $b = 20$.
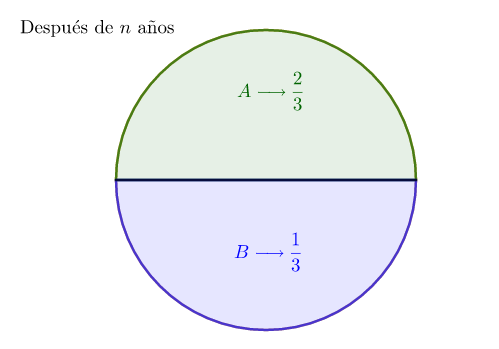
En conclusión, si inicialmente tenemos una población total de 120, entonces la distribución será $(80, 40)$ es decir $\frac{2}{3}$ de la población total en la ciudad $A$ y $\frac{1}{3}$ de la población total en la ciudad $B$.
En el siguiente enlace puedes observar una animación de como los valores de las poblaciones se aproximan al resultado que calculamos, $(80, 40).$