- Sea $X$ un conjunto. La familia $\mathcal{T}_{ind}= \big\{ \emptyset, X \big\}$ es una topología. Se denomina topología indiscreta.
- La familia $\mathcal{T}_{disc} = \mathcal{P}(X)$, donde $\mathcal{P}$ es el conjunto potencia, también es una topología. Se denomina topología discreta.
- Consideremos la métrica Euclidiana y la métrica uniforme $( \infty )$ en $\mathbb{R}^2.$ Comparemos las topologías que inducen estas dos métricas. $$d_{\infty} (x,y) = \big\|x-y \big\|_{\infty}$$ $$d_2 (x, y) = \big\| x \, – \, y \big\|_2$$ $$_2B_1\big( (0, 0) \big) = \big\{(x, y) \in \mathbb{R}^2 \, \big| \, x^2+y^2 < 1 \big\}$$ $$_{\infty}B_1 \big( (0, 0) \big) = \big\{(x, y) \in \mathbb{R}^2 \, \big| \, máx \big\{ |x|, |y| \big\} < 1 \big\}$$
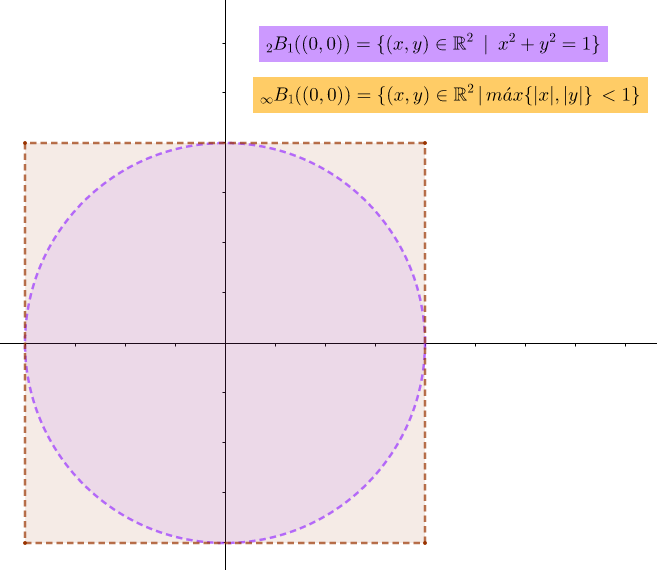
Comparemos $\mathcal{T}_2$ con $\mathcal{T}_{\infty}$. ¡Son la misma topología!
Porque $x$ es un punto interior de $A$ según $\mathcal{T}_2$ $\iff$ existe un círculo con centro en $x$ contenido en $A$ y dentro de ese círculo podemos inscribir un cuadrado. Entonces $x$ es punto interior de $A$ según $\mathcal{T}_{\infty}$.
Recíprocamente $x$ es un punto interior de $A$ según $\mathcal{T} _{\infty}$ $\iff$ existe un cuadrado con centro en $x$ contenido en $A$ y dentro de ese cuadrado podemos inscribir un círculo. Entonces $x$ es punto interior de $A$ según $\mathcal{T}_2$.
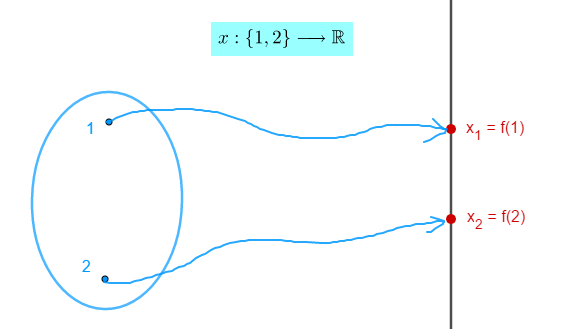
- $\mathbb{R}^2$ puede pensarse como un espacio de funciones.
$$f : \{1, 2\} \longrightarrow \mathbb{R}$$
Al punto $(x_1, x_2)$ le corresponde la función $f$ cuya regla de correspondencia es
$f(1) = x_1$ y $f(2) =x_2$
Entonces $d_{\infty} (f, g) = máx \big\{ \big|f(1) \, – \, g(1) \big|, \big|f(2) \, – \, g(2) \big| \big\}$
En el siguiente enlace puedes observar un dibujo interactivo del ejemplo anterior.
