Curvas parametrizadas

Sea $$ \alpha (t) = (x(t), y(t), z(t))$$ una curva, donde $t$ es el tiempo y $(x(t), y(t), z(t))$ la posición en el espacio.

Es decir, para cada $t$ tenemos que:

$$t \longrightarrow (x(t), y(t), z(t))$$

Y la curva representa el camino que describe.

La derivada de $\alpha (t)$ está dada por:

$$ {\alpha}’ (t) = ({x}'(t), {y}'(t), {z}'(t))$$

$${\alpha}’ (t) = \lim_{\Delta t \to \infty} \dfrac{(\alpha (t_0 \, – \, \Delta t) \, – \, \alpha (t_0))}{\Delta t} $$

Y representa la velocidad instantánea.

La rapidez es $\|{\alpha}’ (t) \|.$

Además, la aceleración instantánea está dada por $${{\alpha}’}’ (t)$$

Movimiento rectilíneo uniforme

Dado el punto $\vec{p_0} (x_0, y_0, z_0)$ que representa la posición inicial.

El vector velocidad constante, está dado por $\vec{v} = (v_1, v_2, v_3).$

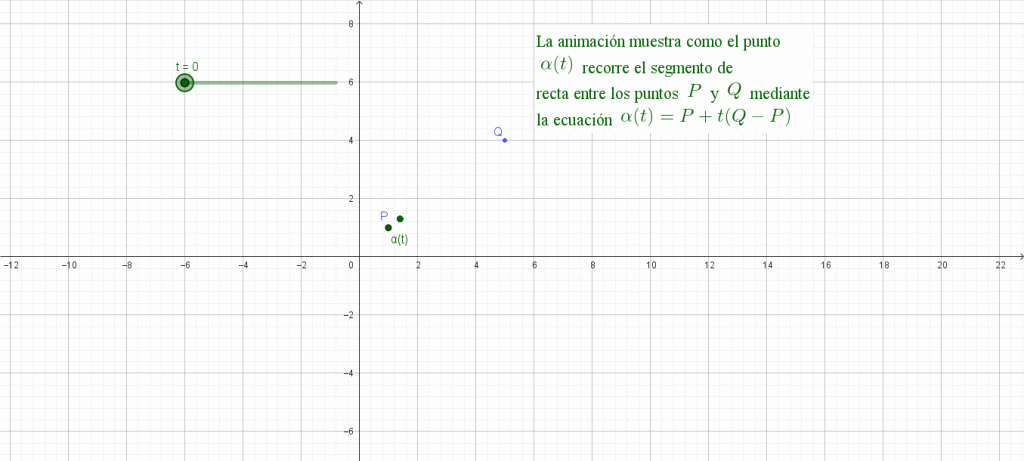
Por lo que, la curva que representa el camino que se describe es: $$ \alpha (t) = \vec{p_0} + \vec{v}(t)$$ $$ \alpha (t) = (x_0, y_0, z_0) +t(v_1, v_2, v_3)$$ $$ \alpha (t) = (x_0 + t v_1, y_0 + t v_2, z_0 + t v_3)$$

La ecuación de la recta tangente es: $$\beta (t) = \alpha (t_0) + t {\alpha}’ (t_0)$$

Existe una recta tangente si ${\alpha}’ (t_0) \neq \vec{0}$.

Si ${\alpha}’ (t_0) = \vec{0}$, estamos diciendo que la velocidad es $0$, es decir, no se mueve, y por tanto $\alpha (t) = \vec{p_0}$ para toda $t.$

Los puntos donde ${\alpha}’ (t_0) = 0$ son excepcionales.

https://www.geogebra.org/classic/spwzzvcr

Movimiento circular uniforme

Dada una circunferencia de radio $r > 0$ con centro en $(h, k)$, posición inicial $(x_0, y_0)$ y velocidad inicial $(x’_0, y’_0)$, analizamos diferentes casos para poder calcular su frecuencia, velocidad angular, periodo, amplitud y fase.

Caso sencillo

Radio $r = 1$

Centro $(h, k) = (0, 0)$

Posición inicial $(x_0, y_0) = (1, 0)$

Velocidad inicial $(x’_0, y’_0) = (0, 1)$

Entonces $\left\{ x(t) = \cos (t) \atop y(t) = \sin (t) \right.$

Tenemos que la rapidez unitaria es $\| {\alpha}’ (t)\| = 1.$

Si el periodo es $2\pi$ entonces, para toda $t$:

$\left\{ x(t + 2\pi) = x (t) \atop y(t + 2\pi) = y (t) \right.$

Por lo que $\vec{\alpha} (t) = \vec{\alpha} (t + 2\pi).$

¿Cómo serian las ecuaciones si el movimiento fuera de $\textcolor{Blue}{periodo \; 1}$?

$\left\{ x(t) = \cos (2\pi t) \atop y(t) = \sin (2\pi t) \right.$

Entonces para $t = 0$ la posición es $ (1, 0)$; y para $ t = 1$ la posición también es $(1, 0).$

Luego, la rapidez de $\left\{ x(t) = \cos (2\pi t) \atop y(t) = \sin (2\pi t) \right.$ es

$\left\{ x’ (t) = -2 \sin (2\pi t) \atop y’ (t) = 2 \cos (2\pi t) \right.$

Por lo que $\|(x’ (t), y'(t)) \| = \sqrt{(2 \pi)^2 (\cos^2 (2\pi t) + \sin^2 (2 \pi t))}$,

es decir que la rapidez es: $$\|(x’ (t), y'(t)) \| = 2 \pi $$

Para periodos $T > 0$

$\left\{ x(t) = \cos \left( \frac{2\pi t}{T} \right) \atop y(t) = \sin \left( \frac{2\pi t}{T} \right) \right.$

Entonces para $t = 0$ la posición es $ (1, 0)$; y para $ t = T$ la posición también es $(1, 0).$

¿Cómo serían las ecuaciones si recorremos la circunferencia en el sentido horario, con periodo $T = 2\pi$?

Entonces $\left\{ x(t) = \cos (t) \atop y(t) = – \sin (t) \right.$

Por lo que $(x'(0), y'(0)) = (0, -1).$

Si ahora cambiamos la posición inicial, digamos que $ \vec{p_0} = (x_0, y_0).$

Dado el punto $(x_0, y_0)$, existe un ángulo $\theta$ tal que:

$\left\{ x_0 = \cos (\theta_0) \atop y_0 = \sin (\theta_0) \right.$

Si $(x_0, y_0) = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \Rightarrow \theta_0 = 45° = \frac{\pi}{4}$

Si $(x_0, y_0) = (\frac{1}{2}, \frac{\sqrt{3}}{2}) \Rightarrow \theta_0 = 60° = \frac{\pi}{3}$

Luego, para toda $t$ se tiene que:

$\left\{ x(t) = \cos (t + \theta_0) \atop y(t) = \sin (t + \theta_0) \right.$

Cumple que $(x(0), y(0)) = (\cos \theta_0, \sin \theta_0) = (x_0, y_0)$, es decir, en el instante $t_0 = 0$ la posición inicial es $(x_0, y_0).$

Si hubiéramos escrito

$\left\{ x(t) = \cos (t – \theta_0) \atop y(t) = \sin (t – \theta_0) \right.$

Entonces $\left\{ x(\theta_0) = 1 \atop y(\theta_0) = 0 \right.$ es decir, en el instante $t_0 = \theta_0$ la posición es $(1, 0).$

Observación:

Si escribimos $\left\{ x(t) = \cos ( – t) = cos (t) \atop y(t) = \sin ( – t) = – \sin (t) \right.$

entonces estamos recorriendo la circunferencia en sentido horario.

Ahora estudiemos el siguiente caso:

$\left\{ x(t) = \cos (w t ) \atop y(t) = \sin (w t ) \right.$

El periodo es $\frac{2 \pi}{T} = \omega \Rightarrow T = \frac{2 \pi}{\omega}.$

Otro caso:

Si tenemos las ecuaciones $\left\{ x(t) = A \cos (w t ) \atop y(t) = A \sin (w t ) \right.$

y $A = 2$ entonces las ecuaciones

$\left\{ x(t) = 2 \cos (w t ) \atop y(t) = 2 \sin (w t ) \right.$

representan una circunferencia de radio 2. $A$ se denomina amplitud.

Caso centro $(h, k)$

Si el centro está en el punto $(h, k)$, entonces:

$$\left\{ x(t) = A \cos (w t ) + h \atop y(t) = A \sin (w t ) + k \right.$$

En el siguiente enlace puedes observar una animación de la parametrización.

https://www.geogebra.org/classic/gpuexq9c

Parametrización de elipses e hipérbolas

La elipse : $$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$$

se puede parametrizar como

$$\left\{ x = a \cos \theta \atop y = b \sin \theta \right.$$

ya que si elevamos al cuadrado ambas ecuaciones obtenemos que $$\left\{ x^2 = a^2 \cos^2 \theta \atop y^2 = b^2 \sin^2 \theta \right.$$ luego, despejando y sumando miembro a miembro observamos que $$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = \cos^2 \theta + \sin^2 \theta = 1$$ que es la ecuación de la elipse.

La hipérbola: $$x^2 – y^2 = 1$$

se puede parametrizar como

$$\left\{ x = \sec \theta \atop y = \tan \theta \right.$$

ya que si elevamos al cuadrado cada ecuación tenemos que $$\left\{ x^2 = \sec^2 \theta \atop y^2 = \tan^2 \theta \right.$$ luego, restándolas vemos que $$ x^2 – y^2 = \sec^2 \theta – \tan^2 \theta = \dfrac{1}{\cos^2 \theta} – \dfrac{\sin^2 \theta}{\cos^2 \theta} = \dfrac{1 – \sin^2 \theta}{\cos^2 \theta} = \dfrac{\cos^2 \theta}{\cos^2 \theta} = 1 $$ obtenemos la ecuación de la hipérbola.

Otra manera de parametrizar la hipérbola es considerando

$$\left\{ x = \cosh \theta = \dfrac{e^t + e^{-t}}{2} \atop y = \sinh \theta = \dfrac{e^t – e^{-t}}{2}\right.$$

$$ x^2 – y^2 = \cosh^2 \theta – \sinh^2 \theta = 1$$

Longitud de arco

Consideramos una curva parametrizada $$\alpha : [a, b] \subset \mathbb{R} \rightarrow \mathbb{R}^2$$ $$\alpha (t) =(x(t), y(t))$$

Sean $P = \alpha (a)$

y $Q = \alpha (b)$

¿Cuál es la longitud de arco desde $P$ hasta $Q$?

• Aproximemos la longitud de la curva como suma de segmentos de recta.

Dibujo A

$\sum\limits_{i = 1}^n \|\alpha (t_i) – \alpha (t_{i-1}) \|$ con la partición $ a = t_0 < t_1 < \dots < t_n = b$

Nos preguntamos si hay un teorema del valor medio. Es decir, existe $\rho \in (a, b)$ tal que $$f(\rho) = \dfrac{f(b) – f(a)}{b – a}$$

Entonces existe $\rho \in (a, b)$ tal que $$\overrightarrow{\alpha}(\rho) = \dfrac{\overrightarrow{\alpha}(b) – \overrightarrow{\alpha}(a)}{b – a} $$

Si así fuera, entonces $$\| {\alpha}'(\rho) \| = \dfrac{\| \overrightarrow{\alpha}(b) – \overrightarrow{\alpha}(a) \|}{b – a} $$

$\sum\limits_{i = 1}^n \|\alpha (t_i) – \alpha (t_{i-1}) \|=\sum\limits_1^n \|\alpha (t_i) – \alpha (t_{i-1}) \|\dfrac{t_i – t_{i-1}}{t_i – t_{i-1}} $

$=\sum\limits_{i = 1}^n \|{\alpha}’ (\xi_i) \| (t_i – t_{i-1})$

Por lo anterior definimos la longitud de arco desde $P$ hasta $Q$ como

$$ \int\limits_a^b \| {\alpha}'(t) \| dt $$

CASO CIRCUNFERENCIA

Para $\omega = 1.$

$x (t) = A \cos (t) + h$

$y (t) = A \sin (t) + k$

Derivando

$x’ (t) = – A \sin (t) \Longrightarrow (x’)^2 (t) = A^2 \sin^2 (t)$

$y’ (t) = A \cos (t) \Longrightarrow (y’)^2 (t) = A^2 \cos^2 (t) $

Sumando ambas igualdades

$(x’)^2 + (y’)^2 = A^2$ por lo que $\| {\alpha}'(t) \| = A.$

Si $P = \alpha (\theta_0)$ y $Q = \alpha (\theta_1)$, entonces

$$ \int\limits_{\theta_0}^{\theta_1} A \, dt = A (\theta_1 – \, \theta_0) = \text{radio } \Delta \theta $$

Una parametrización de una curva en coordenadas polares

Sea $r = f (\theta) $

Donde $\theta = \omega t$ y $ r = f( \omega t)$, que en coordenadas polares es:

$x (t) = f (\omega t) \cos (\omega t)$

$y (t) = f (\omega t) \sin (\omega t)$

Si $\omega = 1$ entonces $\overrightarrow{\alpha} (t) = (x(t), y(t)) = x (t) \vec{e_1} + y (t) \vec{e_2} = r (t) \overrightarrow{\beta} (t)$, donde $\beta (t) = (\cos \theta (t), \sin \theta (t))$

En este caso, ¿cómo calculamos la velocidad?

$x’ (t) = \dfrac{d}{dt} (f(\omega t) \cos (\omega t)) = \omega f'(\omega t) \cos (\omega t) – \sin (\omega t) f(\omega t) \omega$

$y’ (t) = \dfrac{d}{dt} (f(\omega t) \sin (\omega t)) = \omega f'(\omega t) \sin (\omega t) + \cos (\omega t) f (\omega t) \omega$

Luego,

$(x’, y’) = ( \omega f'(\omega t) \cos (\omega t) – \sin (\omega t) f(\omega t) \omega , \omega f'(\omega t) \sin (\omega t) + \cos (\omega t) f(\omega t) \omega )$

$(x’, y’) = \omega f'(\omega t) (\cos (\omega t) , \sin (\omega t) + \omega f(\omega t) ( -\sin (\omega t) , \cos (\omega t)$

$\overrightarrow{\alpha}’ (t) = r’ (t) \overrightarrow{\beta} (t) + r (t) \overrightarrow{\beta}’ (t)$

$\beta$, $\beta’$ son una base de $\mathbb{R}^2$ en la que podemos extresar ${\alpha}’$.

$\vec{e_1}$, $\vec{e_2}$ son otra base de $\mathbb{R}^2$ en la que también podemos extresar ${\alpha}’$.

Luego, $\alpha’ (t) = x’ (t) \vec{e_1} + y’ (t) \vec{e_2} = r’ (t) \overrightarrow{\beta} (t) + r (t) \overrightarrow{\beta}’ (t)$