Introducción
La última de las secciones cónicas que abordaremos en esta unidad es la parábola. De las tres cónicas que hemos revisado, probablemente es la que conoces mejor de forma intuitiva: ya sea que hayas escuchado sobre «las antenas parabólicas», «los espejos parabólicos» o «el tiro parabólico», estamos tan familiarizados con las propiedades de las parábolas que en esta unidad, más allá de introducir la figura como algo nuevo, nos encargaremos de formalizar sus propiedades .
¿Qué hace que la imagen mental que tenemos de las parábolas corresponda tan bien a la figura que podemos obtener a partir de una definición formal? Podrás recordar de tus clases de mecánica de la preparatoria que la Tierra ejerce una fuerza sobre cada uno de los objetos sobre su superficie que les da una aceleración constante, usualmente denotada por la letra $g$. Entonces, la trayectoria de un objeto, asumiendo condiciones ideales, que se mueve con velocidad constante en el eje horizontal y con movimiento acelerado en el eje vertical está descrita por:
\begin{equation}
\begin{aligned}
&x(t)=v_{0} t \cos (\theta) \
&y(t)=v_{0} t \sin (\theta)-\frac{1}{2} g t^{2}
\end{aligned}
\end{equation}
No es necesario que en este momento entiendas totalmente de dónde vienen estas dos ecuaciones; por el momento quédate con la idea de que es un buen modelo matemático de un proyectil en la Tierra que se mueve sobre un plano; es decir, estas dos ecuaciones describen bastante bien el movimiento de una bala de cañón al ser disparada, una pelota de fútbol después de ser pateada, etc. Resulta que estas dos ecuaciones son la parametrización de una parábola, de modo que una parábola es una descripción bastante buena de la trayectoria de un objeto cuando «lo lanzamos». Entonces, aunque estemos por abordar por primera vez el estudio formal de la parábola, verás que tanto sus elementos, como sus propiedades te resultarán bastante familiares.

Sin más preámbulo, pasaremos a la definición de una parábola: además de la definición como conjunto de puntos, obtendremos una ecuación canónica al igual que como lo hicimos para la elipse y la hipérbola y nos familiarizaremos con sus elementos más importantes. Dejaremos la descripción detallada de todos sus elementos y la exposición de sus propiedades para la siguiente entrada.
Definición de Parábola
Una parábola es el lugar geométrico de los puntos que equidistan de un punto $\mathbf{p}$ (llamado su foco) y una recta $\ell$, llamada su directriz, donde $\mathbf{p} \notin \ell$. Es decir, está definida por la ecuación
\begin{equation}
\mathrm{d}(\boldsymbol{x}, \boldsymbol{p})=\mathrm{d}(\boldsymbol{x}, \ell).
\end{equation}
En el siguiente recuadro interactivo de GeoGebra juega un poco con esta definición. Observa cómo una parábola, a primera vista, podría parecerte una elipse «cortada», pero date cuenta que es una curva que se dibuja a partir de una condición muy específica que se impone a una distancia entre la recta directriz y el foco ¿Puedes encontrar los casos degenerados de la parábola?¿Qué pasa si haces $p=0$?
Tomando un ejemplo sencillo con el foco en el eje $\mathbf{y}$, la directriz paralela al eje $\mathbf{x}$, y que además pase por el origen. Tenemos entonces $\mathbf{p}=(0, \mathrm{c})$, donde $\mathrm{c}>0$ digamos, y $\ell: \mathrm{y}=-\mathrm{c}$; de tal manera que la parábola queda determinada por la ecuación
\begin{equation}
\sqrt{x^{2}+(y-c)^{2}}=|y+c|.
\end{equation}
Como te puedes dar cuenta, lo único que hicimos fue aplicar la definición de norma en $\mathbb{R}^{2}$ tal como la estudiamos en la primera unidad. Como ambos lados de la ecuación son positivos, ésta es equivalente a la igualdad de sus cuadrados que da
\begin{equation}
\begin{aligned}
x^{2}+y^{2}-2 c y+c^{2} &=y^{2}+2 c y+c^{2} \
x^{2} &=4 c y.
\end{aligned}
\end{equation}
De tal manera que la gráfica de la función $x^{2}$ ($y=x^{2}$) es una parábola con foco $(0,\frac{1}{4})$ y directriz $y=-\frac{1}{4}$. Veremos ahora que cualquier parábola cumple la propiedad de «ser gráfica de una función» respecto de su directriz.
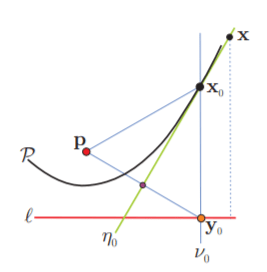
Sea $\mathcal{P}$ la parábola con foco p y directriz $\ell$ (donde $\mathbf{p} \notin \ell)$. Dado un punto $\mathbf{y}_{0} \in \ell$, es claro que los puntos del plano cuya distancia a $\ell$ coincide con (o se mide por) su distancia a $\mathbf{y}_{0}$ son precisamente los de la normal a $\ell$ que pasa por $\mathbf{y}_{0}$, llamémosla $v_{0} .$ Ver la figura.
Por otro lado, la mediatriz entre $\mathbf{y}_{0}$ y $\mathbf{p}$, llamémosla $\eta_{0}$, consta de los puntos cuyas distancias a $\mathbf{p}$ y $\mathbf{y}_{0}$ coinciden. Por lo tanto, la intersección de $\eta_{0}$ y $v_{0}$ está en la parábola $\mathcal{P}$, es decir $\boldsymbol{x}_{0}=v_{0} \cap \eta_{0} \in \mathcal{P}$ pues $\mathrm{d}\left(\boldsymbol{x}_{0}, \ell\right)=\mathrm{d}\left(\boldsymbol{x}_{0}, \mathbf{y}_{0}\right)=\mathrm{d}\left(\boldsymbol{x}_{0}, \boldsymbol{p}\right)$. Pero además $\mathbf{x}_{0}$ es el único punto en la normal $v_{0}$ que está en $\mathcal{P}$. Ésta es «la propiedad de la gráfica» a la que nos referíamos.
Podemos concluir aún más: que la mediatriz $\eta_{0}$ es la tangente a $\mathcal{P}$ en $\mathbf{x}_{0}$. Pues para cualquier otro punto $x \in \eta_{0}$ se tiene que su distancia a $\ell$ es menor que su distancia a $\mathbf{y}_{0}$ que es su distancia a $\mathbf{p}\left(\mathrm{d}(\mathbf{x}, \ell)<\mathrm{d}\left(\mathbf{x}, \mathbf{y}_{0}\right)=\mathrm{d}(\mathbf{x}, \mathbf{p})\right)$, y entonces $x \notin \mathcal{P}$. De hecho, la parábola $\mathcal{P}$ parte el plano en dos pedazos, los puntos más cerca de $\mathbf{p}$ que de $\ell$ (lo de adentro, digamos, definidos por la desigualdad $d(\mathbf{x}, \mathbf{p}) \leq d(\mathbf{x}, \ell)$) y los que están más cerca de $\ell$ que de $\mathbb{p}$ (lo de afuera, dado por $d(\mathbf{x}, \ell) \leq d(\mathbf{x}, \mathbf{p})$ en donde está $\eta_{0}$), que comparten la frontera donde estas distancias coinciden (la parábola $\mathcal{P}$). Así que $\eta_{0}$ pasa tangente a $\mathcal{P}$ en $\mathbf{x}_{0}$, pues $\mathbf{x}_{0} \in \eta_{0} \cap \mathcal{P}$ y además $\eta_{0}$ se queda de un lado de $\mathcal{P}$.
En el siguiente recuadro interactivo de GeoGebra familiarizate con la expresión analítica de la parábola y nota una cosa muy importante: ¿qué pasa cuando, contrario al caso «sencillo» que vimos en esta entrada, el vértice de la parábola está fuera del origen? Nota cómo una traslación de nuestro caso sencillo introduce un término lineal en la ecuación de la parábola y date cuenta qué papel juega cada uno de los coeficientes modificando la forma de la parábola.
Más adelante…
En esta entrada iniciamos nuestro estudio de las parábolas: a partir de su definición como el conjunto de puntos que equidistan de una recta y un punto construimos la curva y nos familiarizamos con su expresión analítica. Así como lo hicimos para las cónicas anteriores, le dedicaremos la siguiente sección a estudiar sus propiedades y a nombrar cada uno de sus elementos; posteriormente, haremos algunos ejercicios para tener práctica leyendo la información geométrica que contiene la ecuación de la parábola.
Tarea moral
- Construye la curva y da el dominio y codominio de las siguientes curvas: $y^{2}=16x$, $x^{2}=-16y$, $x^{2}=10y$, $y^{2}=7x$, $3x^{2}+5y=0$, $5x^{2}-2y=0$, $y^{2}+6x=0$, $x^{2}=11y$.
- A partir de la definición de parábola, encuentre la ecuación de la parábola de foco $(0,-5)$ y directriz $y=3$.
- Cuáles son los puntos de intersección de la línea que tiene la ecuación $2x+3y=7$ y la parábola con ecuación $y=-2x^{2}+2x+5$
Entradas relacionadas
- Ir a Geometría Analítica I
- Entrada anterior del curso: Problemas con hipérbolas
- Siguiente entrada del curso: Propiedades de parábolas