Introducción
Dada una sucesión, si «quitamos» cierta cantidad de términos de tal forma que aún queda una cantidad infinita de ellos y se conserva el orden de la sucesión original, se genera un tipo particular de sucesión llamado subsucesión. En esta entrada probaremos algunas de sus características y veremos cómo se enlazan sus propiedades respecto a la sucesión original.
Subsucesiones
Primero formalizaremos la idea intuitiva dada en la introducción a través de la siguiente definición.
Definición. Sea $\{a_n\}$ una sucesión de números reales y sea $n_1 < n_2 < \ldots < n_k < \ldots$, con $k \in \mathbb{N}$, una sucesión estrictamente creciente de números naturales. Entonces la sucesión $\{ a_{n_k} \}$ dada por $$\{ a_{n_1}, a_{n_2}, \ldots, a_{n_k}, \ldots \}$$
es una subsucesión de $\{a_n\}$.
Observación. Es importante recalcar que en la definición se indica que los índices de los términos de la subsucesión son una sucesión por sí mismos. Esto se podrá apreciar claramente en los ejemplos siguientes.
Ejemplo 1. Consideremos la sucesión $\{ a_n \} = \{ \frac{1}{n} \}$.
Si tomamos los términos con índice par, obtenemos la subsucesión $\{ a_2, a_4, a_6, \ldots, a_{2k}, \ldots \}$ cuyos términos son
$$\left\lbrace \frac{1}{2}, \frac{1}{4}, \frac{1}{6}, \ldots, \frac{1}{2k}, \ldots \right\rbrace.$$
De esta forma, se tiene que $n_1 = 2$, $n_2 = 4$, $\ldots$, $n_k = 2k$, $\ldots$. Y podemos observar que los índices forman una sucesión estrictamente creciente, es decir, se cumple que $$n_1 < n_2 < \ldots < n_k < \ldots.$$
Si consideramos ahora $n_k = 2k-1$, obtenemos una nueva subsucesión $\{ a_1, a_3, a_5, \ldots, a_{2k-1}, \ldots \}$ conformada por los términos
$$\left\lbrace \frac{1}{1}, \frac{1}{3}, \frac{1}{5}, \ldots, \frac{1}{2k-1}, \ldots \right\rbrace.$$
Otra subsucesión podría ser la generada por los índices $n_k = k^2$, generando la subsucesión $\{ a_1, a_4, a_9, \ldots, a_{k^2} \}$, con términos
$$\left\lbrace \frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \ldots, \frac{1}{k^2}, \ldots \right\rbrace.$$
En contraste, podemos observar que $\{a_2, a_1, a_4, a_3, \ldots, a_{k+1}, a_{k-1}, \ldots \}$ no es una subsucesión de $\{ a_n \}$. Los términos generados son
$$\left\lbrace \frac{1}{2}, \frac{1}{1}, \frac{1}{4}, \frac{1}{3}, \ldots, \frac{1}{k+1}, \frac{1}{k-1}, \ldots \right\rbrace.$$
Y no es subsucesión debido a que ésta no respeta el orden de la sucesión original, en otras palabras, la sucesión de índices $\{n_k\}$ no es estrictamente creciente. En este caso
$$n_k = \begin{cases} k+1 & \text{ si } k \text{ es impar} \\ k-1 & \text{ si } k \text{ es par}. \end{cases}$$
Con lo cual podemos ver que $n_1 = 2$, $n_2=1$, $n_3 = 4$, $n_4 = 3$, $\ldots$, por lo que $\{n_k\}$ no es monótona y, particularmente, no es estrictamente creciente.
Una forma singular de crear subsucesiones a partir de una sucesión dada, es eliminando los primeros $m$ términos de la sucesión. Así, tenemos la siguiente definición.
Definición. Sea $\{a_n\}$ una sucesión de números reales y sea $m \in \mathbb{N}$. Definimos la cola-$m$ de $\{a_n\}$ como la sucesión
$$\{a_{m+n}: n \in \mathbb{N}\} = \{ a_{m+1}, a_{m+2}, \ldots \}.$$
La cola-$m$ es una subsucesión donde $n_1 = m+1$, $n_2 = m +2$, $\ldots$, $n_k = m+k$.
Ejemplo 2. Consideremos la sucesión $\{a_n\} = \{ \sqrt{n} \}.$
La cola-$10$ de $\{a_n\}$ es la subsucesión $\{ a_{11}, a_{12}, \ldots, a_k \ldots \}$, cuyos términos son $\{ \sqrt{11}, \sqrt{12}, \ldots, \sqrt{k}, \ldots \}.$
Subsucesiones de sucesiones convergentes
Si generamos una subsucesión de una sucesión convergente, es natural que dicha subsucesión también converja y, de hecho, lo hace al límite de la sucesión original.
Teorema. Si una sucesión $\{a_n\}$ de números reales converge a un número real $L$, entonces cualquier subsucesión $\{ a_{n_k}\}$ también converge a $L$.
Demostración.
Sea $\varepsilon > 0$. Como $\{a_n\}$ converge a $L$, entonces existe un número natural $n_0 \in \mathbb{N}$ tal que para todo $n \geq n_0$ se tiene que
$$|a_n – L| < \varepsilon.$$
Dado que $n_1 < n_2 < \ldots < n_k < \ldots$ es una sucesión creciente de números naturales, se tiene que $n_k \geq k$. De esta forma, tenemos que si $k \geq n_0$, entonces $n_k \geq k \geq n_0$. Por lo que se cumple que
$$|a_{n_k} – L| < \varepsilon.$$
Por lo tanto, la sucesión $\{ a_{n_k} \}$ también converge a $L$.
$\square$
Ejemplo 3. Del teorema anterior se sigue que dada una sucesión $\{a_n\}$ convergente a $L$, la cola-$m$ de la sucesión también converge a $L$ para todo $m \in \mathbb{N}$.
Ejemplo 4. Consideremos la sucesión $\{a_n\} = \{ \frac{1}{\pi^n}\}$.
Notemos que $\frac{1}{\pi^n} = \left( \frac{1}{\pi} \right)^n$.
Además, como $\pi > 1$, entonces $\frac{1}{\pi} <1$. Por tanto $$\lim_{n \to \infty} \frac{1}{\pi^n} = 0.$$
Así, toda subsucesión de $\{a_n\}$ converge a cero. Podemos considerar, por ejemplo, la subsucesión generada tomando $n_k = 2k$, es decir, la subsucesión $\{a_{n_k} \} = \{ \frac{1}{\pi^{2k}} \}$ converge a cero.
Subsucesiones y la no convergencia
Hasta este punto hemos revisado las subsucesiones y su relación con la convergencia; ahora es momento de encontrar qué sucede respecto a la no convergencia.
Teorema. Sea $\{a_n\}$ una sucesión de números reales. Entonces los siguientes enunciados son equivalentes:
- La sucesión $\{a_n\}$ no converge a $L \in \mathbb{R}.$
- Existe $\varepsilon_0 > 0$ tal que para cualquier $k \in \mathbb{N}$, existe $n_k \in \mathbb{N}$ tal que $n_k \geq k$ y $|a_{n_k} – L| \geq \varepsilon_0.$
- Existe $\varepsilon_0 > 0$ y una subsucesión $\{a_{n_k}\}$ de $\{a_n\}$ tal que $|a_{n_k} – L| \geq \varepsilon_0$ para todo $k \in \mathbb{N}.$
Demostración.
$1 \Rightarrow 2]$ Si $\{a_n\}$ no converge, entonces existe $\varepsilon_0 > 0$ para el cual no es posible encontrar un natural $k$ tal que para todo $n \geq k$ se cumpla $|a_n-L| < \varepsilon$. Es decir, para todo $k \in \mathbb{N}$ existe un natural $n_k \geq k$ tal que $|a_{n_k} – L | \geq \varepsilon_0.$
$2 \Rightarrow 3]$ Sea $\varepsilon_0 > 0$ tal que cumple $2)$ y sea $n_1 \in \mathbb{N}$ tal que $n_1 \geq 1$ y $|a_{n_1} – L| \geq \varepsilon_0.$
Ahora sea $n_2 \in \mathbb{N}$ tal que $n_2 > n_1$ y $|a_{n_2} – L| \geq \varepsilon_0.$
Sea $n_3 \in \mathbb{N}$ tal que $n_3 > n_2$ y $|a_{n_3} – L| \geq \varepsilon_0.$
Se continúa de esta manera para obtener la subsucesión $\{a_{n_k}\}$ tal que $|a_{n_k} – L| \geq \varepsilon_0$ para todo $k \in \mathbb{N}.$
$3 \Rightarrow 1]$ Supongamos que $\{a_n\}$ tiene una subsucesión $\{a_{n_k}\}$ que satisface la condición $3)$. Entonces $\{a_n\}$ no puede converger a $L$ porque sería una contradicción al teorema anterior.
$\square$
Criterios de no convergencia. Sea $\{a_n\}$ una sucesión de números reales. Si se cumple cualquiera de las siguientes condiciones, entonces la sucesión es divergente.
- $\{a_n\}$ tiene dos subsucesiones convergentes $\{a_{n_k}\}$ y $\{a_{n_l}\}$. Donde $\{a_{n_k}\}$ converge $L$ y $\{a_{n_l}\}$ converge a $M$, pero $L \neq M.$
- $\{a_n\}$ no está acotada.
Ejemplo 5. Prueba que la sucesión $\{(-1)^n\}$ no es convergente.
Demostración.
Consideremos las subsucesiones $\{(-1)^{2k}\}$ y $\{(-1)^{2k-1}\}$. Es claro que la primera subsucesión converge a $1$, mientras que la segunda converge a $-1$. Por tanto, la sucesión no converge.
$\square$
Ejemplo 6. Prueba que la sucesión $\{n!\}$ no es convergente.
Demostración.
Dado que $n! \geq n$ para todo $n \in \mathbb{N}$, y sabemos que la sucesión generada por los números naturales no está acotada. Se sigue que la sucesión $\{n!\}$ no está acotada. Por tanto, no es convergente.
$\square$
Ejemplo 7. Prueba que la sucesión $\{ 1 – (-1)^n + \frac{1}{n} \}$ no es convergente.
Demostración.
Consideremos las subsucesiones $\{ 1 – (-1)^{2k} + \frac{1}{2k} \}$ y $\{ 1 – (-1)^{2k-1} + \frac{1}{2k-1} \}.$
Notemos que
\begin{align*}
\lim_{k \to \infty } 1 – (-1)^{2k} + \frac{1}{2k} & = \lim_{k \to \infty } 1 – ((-1)^2)^k + \frac{1}{2k} \\ \\
& = \lim_{k \to \infty } 1 – (1)^k + \frac{1}{2k} \\ \\
& = 1-1+0 \\ \\
& = 0.
\end{align*}
Análogamente, se tiene que
\begin{align*}
\lim_{k \to \infty } 1 – (-1)^{2k-1} + \frac{1}{2k-1} & = \lim_{k \to \infty } 1 – (-1)^{2k} \cdot (-1)^{-1} + \frac{1}{2k-1} \\ \\
& = \lim_{k \to \infty } 1 – (1)^k \cdot (-1) + \frac{1}{2k-1} \\ \\
& = 1+1+0 \\ \\
& = 2.
\end{align*}
Por tanto, la primera subsucesión converge a $0$, mientras que la segunda converge a $2$. Se concluye que la sucesión $\{ 1 – (-1)^n + \frac{1}{n} \}$ no es convergente.
$\square$
Teorema de Bolzano-Weierstrass
El teorema de Bolzano-Weierstrass nos indica que toda sucesión acotada tiene una subsucesión convergente. Un ejemplo claro es el revisado en esta entrada, la sucesión $\{(-1)^n\}$ de la cual hemos probado anteriormente que está acotada y es fácil notar que la subsucesión generada por los índices pares $n_k =2k$ es convergente. Sin embargo, para probar el caso general, veremos primero que toda sucesión tiene una subsucesión monótona y, usando un teorema previamente revisado que indica que toda sucesión monótona acotada es convergente, podremos probar fácilmente el teorema de Bolzano-Weierstrass.
Teorema. Si $\{a_n\}$ es una sucesión de números reales, entonces existe una subsucesión $\{a_{n_k} \}$ que es monótona.
Demostración.
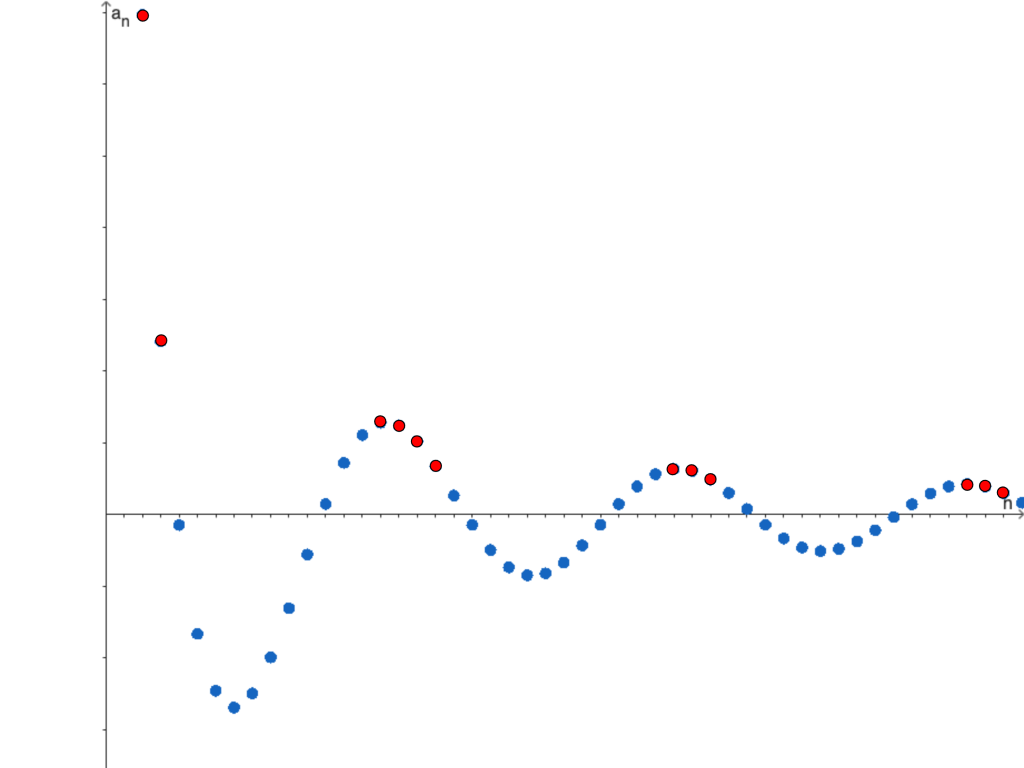
Por practicidad, diremos que $a_m$ es un «pico» si $a_m \geq a_n$ para todo $n \geq m$. Es decir, $a_m$ nunca es excedido por ningún término posterior en la sucesión. Tal como se muestra en la siguiente ilustración, donde los puntos rojos representan los «picos» de la sucesión.
Podemos notar que en una sucesión decreciente cualquier término es un pico, mientras que para una sucesión creciente ningún término es un pico. Dada una sucesión, podemos dividir en dos casos de acuerdo a la cantidad de picos que ésta posea.
- Caso 1: La sucesión tiene una cantidad infinita de picos.
En este caso, la enumeración de los picos se hace con subíndices crecientes: $a_{m_1}$, $a_{m_2}$, $\ldots$, $a_{m_k}$, $\ldots$ Puesto que cada término es un pico se tiene que
$$ a_{m_1} \geq a_{m_2} \geq \ldots \geq a_{m_k}.$$
Por tanto, la subsucesión $\{ a_{m_k}\}$ es una subsucesión decreciente de $\{ a_n\}$. - Caso 2: La sucesión tiene una cantidad finita de picos.
Nuevamente, la sucesión generada por los subíndices es creciente: $a_{m_1}$, $a_{m_2}$, $\ldots$, $a_{m_k}$. Sea $s_1 = m_k+1$ el primer índice después del último pico, entonces existe $s_2 > s_1$ tal que $a_{s_1} < a_{s_2}$ dado que $a_{s_1}$ no es un pico. Además, sucede que $a_{s_2}$ tampoco es un pico, por lo que existe $s_3 > s_2$ tal que $a_{s_2} < a_{s_3}$. Al continuar de esta forma, se obtiene una subsucesión creciente $\{ a_{s_k}\}$ de $\{a_n\}.$
De ambos casos podemos concluir que toda sucesión tiene una subsucesión monótona.
$\square$
Teorema de Bolzano-Weierstrass. Toda sucesión acotada de números reales tiene una subsucesión convergente.
Demostración.
Sea $\{a_n\}$ una sucesión acotada. Por el teorema anterior, sabemos que $\{a_n\}$ tiene una subsucesión monótona $\{a_{n_k}\}$, además la subsucesión también está acotada pues $\{a_n\}$ lo está, entonces $\{a_{n_k}\}$ es convergente.
$\square$
Como último teorema, revisaremos que si toda subsucesión convergente de una sucesión acotada tiene límite $L$, entonces debe suceder que la sucesión original también converja a $L$.
Teorema. Sea $\{a_n\}$ una sucesión acotada de números reales. Si toda subsucesión convergente $\{a_{n_k} \}$ de $\{a_n\}$ converge a $L$, entonces $\{a_n\}$ también converge y lo hace a $L$.
Demostración.
Sea $\{a_n\}$ una sucesión acotada tal que todas sus subsucesiones convergentes lo hacen a $L$. Entonces existe $M \in \mathbb{R}$ tal que $|a_n| < M$ para todo $n \in \mathbb{N}$.
Supongamos que $\{a_n\}$ no converge a $L$, entonces existen $\varepsilon_0 > 0$ y una subsucesión $\{a_{n_k}\}$ tal que
$$|a_{n_k} – L| \geq \varepsilon_0 \quad \forall k \in \mathbb{N}. \tag{1}$$
Puesto que $\{ a_{n_k}\}$ es una subsucesión de $\{a_n\}$, entonces también se cumple que $|a_{n_k}| < M $. Es decir, $M$ también es una cota $\{ a_{n_k}\}$. Por el teorema de Bolzano-Weierstrass, esto implica que $\{a_{n_k}\}$ tiene una subsucesión convergente $\{a_{r_k}\}$. Puesto que esta última subsucesión también es subsucesión de $\{a_n\}$ converge a $L$ por hipótesis. Por tanto, existe $n_0 \in \mathbb{N}$ tal que para $r_k \geq n_0$ se tiene que $|a_{r_k} – L| \leq \varepsilon_0$, lo cual contradice $(1).$
$\square$
Más adelante…
En la siguiente entrada estudiaremos las sucesiones de Cauchy, las cuales nos permitirán dar un enfoque especial a las sucesiones convergentes donde no será necesario conocer a priori el valor del límite. Además, probaremos la equivalencia existente entre las sucesiones convergentes y las sucesiones de Cauchy.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Da un ejemplo de una sucesión y dos subsucesiones de ella.
- Da un ejemplo de una sucesión acotada que tenga una subsucesión convergente.
- Da un ejemplo de una sucesión no acotada que tenga una subsucesión convergente.
- Prueba que la sucesión $\{ \left( 1 + \frac{1}{n^2} \right) ^{n^2} \}$ es convergente.
- Determina el límite de la sucesión$\{ (3n)^{\frac{1}{2n}} \}$.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Sucesiones divergentes y sus propiedades
- Siguiente entrada del curso: Sucesiones de Cauchy
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»