(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
Siendo la última entrada de la Unidad 4, está dedicada a un ejemplo que se justifica usando el Tercer Teorema de Sylow que vimos en la entrada anterior. Por lo mismo, es mucho más corta de lo que estamos acostumbrados, pero es importante para reforzar el conocimiento antes aprendido.
Ilustrando el TTS
Veamos un ejemplo del Tercer Teorema de Sylow.
Ejemplo.
Tomemos $G = S_4$ y veamos la factorización en primos del orden de $G$, $|G| = 24 = 2^3\cdot 3$.
Primero, consideremos al $3$. Notamos que $\left< (1\;2\; 3)\right>$ es un $3$-subgrupo de Sylow ya que tiene $3$ elementos y no podemos encontrar subgrupos de Sylow de $9, 27$ u otra potencia de $3$, porque esta no dividiría al orden de $G$.
Ahora nos preguntamos ¿cuál es la cantidad de $3$-subgrupos de Sylow, denotada por $r_3$? Bueno, por el Tercer Teorema de Sylow sabemos que se cumple:
\begin{align*}
r_3 \,| \, 2^3 \cdot 3 \, \text{ y } \, r_3\equiv 1 \text{(mód }3).
\end{align*}
Como $3 \equiv 0\text{(mód }3)$, entonces $r_3$ no es un múltiplo de $3$, así que $r_3$ tiene que ser un divisor de $2^3 = 8$ congruente con uno módulo $3$, por lo que $r_3 \in \{1, 4\}$.
Pero podemos encontrar $\left< (2\; 3\; 4)\right>$, otro $3$-subgrupo de Sylow diferente al anterior, así que $ r_3 = 4$. Los otros $3$-subgrupos de Sylow son $\left<(1\;3\;4)\right>$ y $\left<(1\;2\;4)\right>$.
Ahora nos fijamos en el primo $2$. Por el TTS, la cantidad de $2$-subgrupos de Sylow ($r_2$) tiene que cumplir,
\begin{align*}
r_2\,| \,2^3 \cdot 3 \, \text{ y } \, r_2\equiv 1 \text{(mód }2).
\end{align*}
La condición del módulo nos indica que $r_2$ es impar, por lo que tiene que ser divisor de $3$ para además se cumpla la primera condición, esto nos deja con $r_2 \in \{1,3\}.$
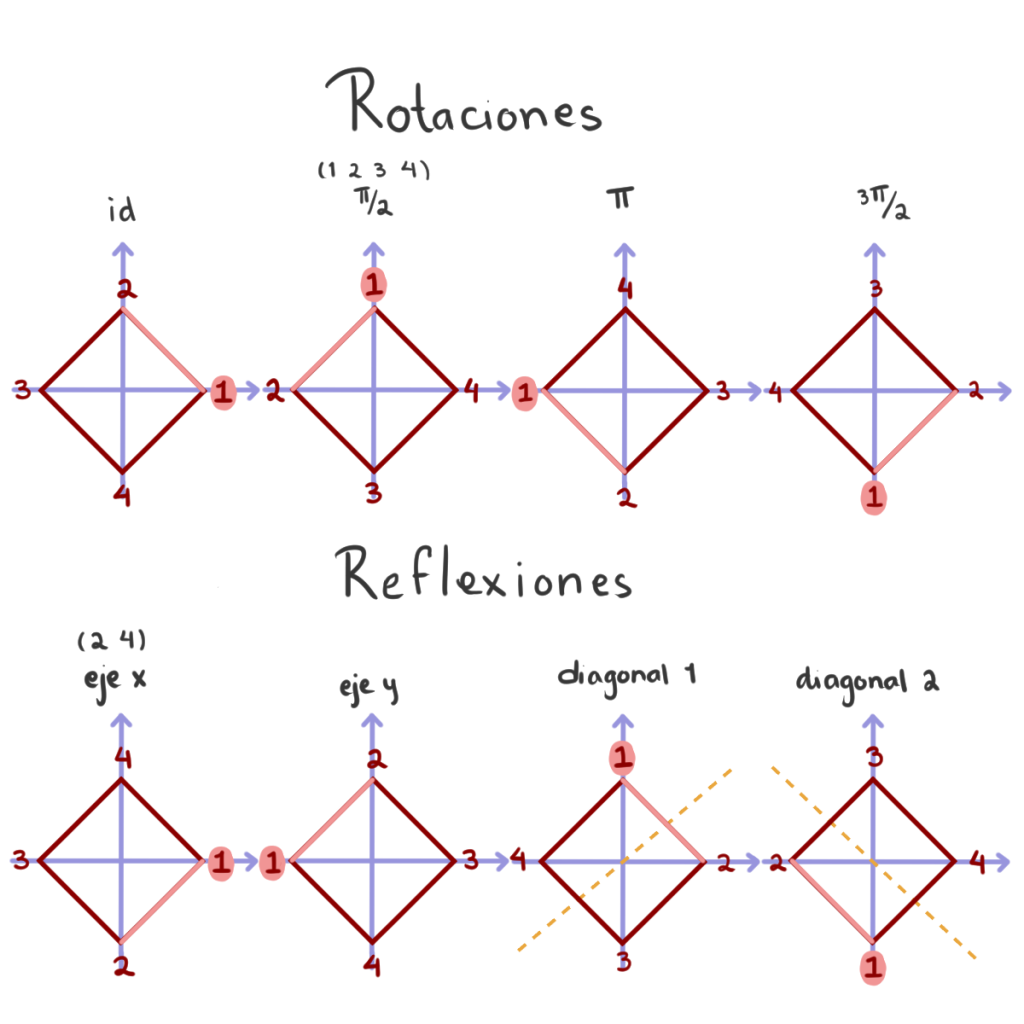
Busquemos estos $2$-subgrupos de Sylow. Sabemos que cada $2$-subgrupo de Sylow tiene orden igual a la máxima potencia de $2$ que divide a $|G|$, esto es 8. Sabemos que si tenemos un cuadrado y numeramos los vértices, podemos codificar cada simetría del cuadrado con una permutación de $S_4$. Recordemos que no toda permutación de $S_4$ es una simetría, pero sí al revés.
Las simetrías de un cuadrado son $8$ en total y estas simetrías pueden ser generadas por la combinación de una rotación y la reflexión con respecto al eje $x$. Como hay $8$ simetrías del cuadrado y éstas pueden ser codificadas en permutaciones de $S_4$, tendremos un subgrupo de $S_4$ de orden $8$, es decir, un $2$-subgrupo de Sylow.
Supongamos que numeramos los vértices de un cuadrado $1,\,2,\,3,\,4$ como en la imagen, entonces la rotación estará dada por $(1\;2\;3\;4)$ y la reflexión con respecto al eje $x$ sería $(2\;4)$. Así, el $2$-subgrupo de Sylow que obtenemos es $\left<(1\;2\;3\;4), (2\;4)\right>$.
Estamos buscando todos los $2$-subgrupos de Sylow posibles, como $r_2 \in \{1,3\}$ bien podíamos pensar que $\left<(1\;2\;3\;4), (2\;4)\right>$ es el único. Pero podemos nombrar los vértices del cuadrado de manera distinta para que las simetrías de $S_4$ que le correspondan cambien y encontremos otro $2$-subgrupo de Sylow.
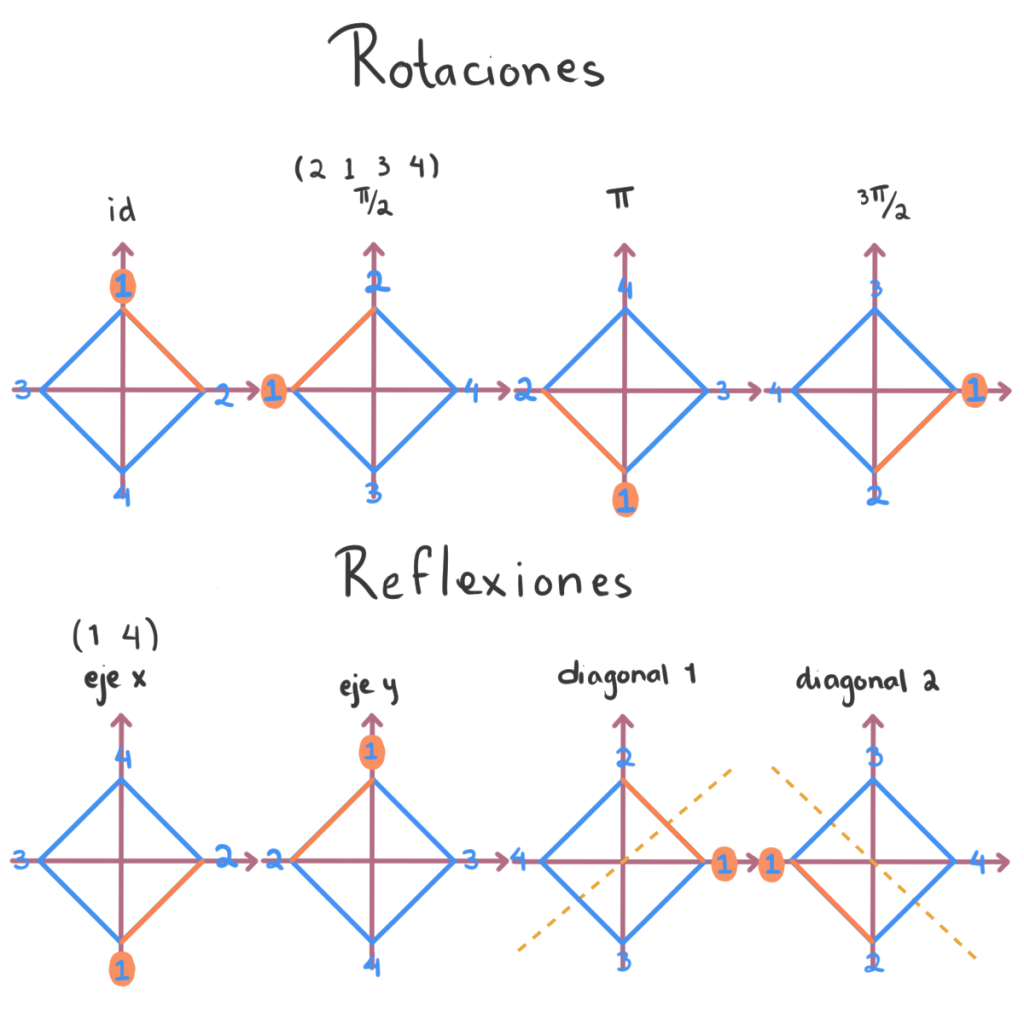
Numerando los vértices del cuadrado $2,\,1,\,3,\,4$ como en la imagen, encontramos que la simetrías están generadas por la rotación $(2\;1\;3\;4)$ y la reflexión $(1\;4)$. Así $\left<(2\;1\;3\;4), (1\;4)\right>$ es otro $2$-subgrupo de Sylow.
Si nos damos cuenta, lo único que hicimos en este cuadrado fue intercambiar los vértices $1$ y $2$ del cuadrado. Esto nos da un subgrupo diferente al anterior porque ese cambio no es una simetría del cuadrado.
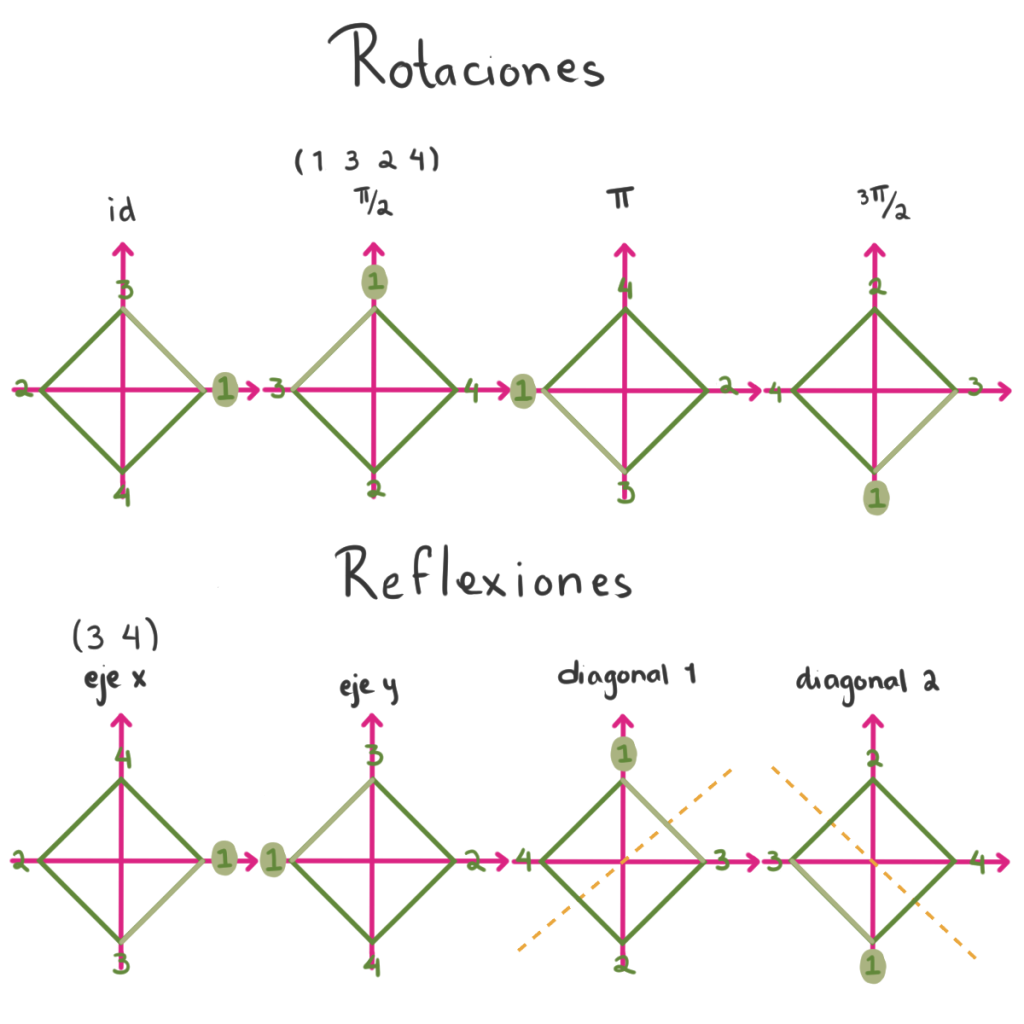
Pero $r_2 = 1$ o $r_2 = 3$, así que no puede haber sólo dos $2$-subgrupos de Sylow, deben ser $3$. Nos queda entonces otro $2$-subgrupo de Sylow por encontrar. Análogamente, tomamos el cuadrado numerando los vértices $1, \, 3, \, 2, \, 4$, donde sólo intercambiamos los vértices $3$ y $4$ del cuadrado original. En este caso nos encontramos que sus simetrías son generadas por $\left< (1\;3\;2\;4), (3\; 4)\right>$ y este es el último $2$-subgrupo de Sylow que nos faltaba.
Así, encontramos todos los subgrupos de Sylow de $S_4$.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Considera el grupo de los cuaternios $Q_8$, ¿cuántos y cuáles son sus $2$-subgrupos de Sylow?
- Busca los $2$ y $3$-subgrupos de Sylow de $\z_6.$
- Sean $a, b \in G : = S_3 \times \z_4$, donde $a = ((1\; 2\; 3), [2])$ y $b = ((1\; 3), [1]).$ Considere el subgrupo $T : = \left< a, b \right> \leq G.$ Prueba que $$T = \left< a,b : a^6 = 1_G, b^2 = a^3 = (ab)^2\right>$$ y que $T$ es un grupo no abeliano con $12$ elementos.
La notación anterior se lee como $T$ es el generado por los elementos $a$ y $b$ tales que $a^6 = 1_G, \,b^2 = a^3 = (ab)^2$.
Más adelante…
Con esta entrada no sólo concluimos en tema de los Teoremas de Sylow, si no también la unidad 4 del curso. ¡Felicidades! Sigue avanzando, ya casi acabamos.
En la siguiente unidad planeamos estudiar el Teorema fundamental de los grupos abelianos finitos. Pero para ello comenzaremos viendo una forma sencilla de construir nuevos grupos a partir de una cantidad finita de grupos previos.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Teoremas de Sylow.
- Siguiente entrada del curso: Producto directo externo.
- Resto de cursos: Cursos.