Introducción
En la entrada anterior establecimos una versión local, para discos, del teorema integral de Cauchy y vimos que una primera consecuencia de este resultado es la fórmula integral de Cauchy, la cual nos permitió establecer la existencia de las derivadas de todos los órdenes de una función analítica en un dominio.
En esta entrada probaremos algunas otras consecuencias de este teorema tan importante en el Análisis Complejo, como el teorema de Liouville, el teorema Fundamental del Álgebra, el teorema de Morera, entre otros.
Proposición 37.1. (Desigualdad de Cauchy.)
Sean $D\subset\mathbb{C}$ un dominio, $f:D\to\mathbb{C}$ una función analítica en $D$, $z_0\in D$ y $r>0$ tal que $C(z_0, r) \subset D$. Entonces:
\begin{equation*}
\left| f^{(n)}(z_0)\right| \leq \frac{n! M_r}{r^n}, \quad \forall n\in\mathbb{N},
\end{equation*}donde $M_r:=\max\limits_{z\in C(z_0,r)}|f(z)|$.
Demostración. Dadas las hipótesis, sea $M_r:=\max\limits_{z\in C(z_0,r)}|f(z)|$.
Como $f$ es analítica en $D$, en particular lo es en $z_0$, por lo que de la proposición 36.5 tenemos que las derivadas de todos los ordenes de $f$ en $z_0$ existen en el interior de la circunferencia $C(z_0, r) \subset D$ y están dadas por:
\begin{equation*}
f^{(n)}(z_0) = \frac{n!}{2\pi i}\int_{C(z_0, r)} \frac{f(z)}{(z-z_0)^{n+1}} dz,
\end{equation*}por lo que, de la proposición 34.3(5) se sigue que:
\begin{align*}
\left|f^{(n)}(z_0)\right| & = \left|\frac{n!}{2\pi i}\int_{C(z_0, r)} \frac{f(z)}{(z-z_0)^{n+1}} dz\right|\\
& = \frac{n!}{2\pi} \left|\int_{C(z_0, r)} \frac{f(z)}{(z-z_0)^{n+1}} dz\right|\\
& \leq \frac{n!}{2\pi} \int_{C(z_0, r)} \frac{\left|f(z)\right|}{\left|z-z_0\right|^{n+1}}\,|dz|\\
& \leq \frac{n!}{2\pi} \frac{M_r}{r^{n+1}} \int_{C(z_0, r)} |dz|\\
& = \frac{n!}{2\pi} \frac{2\pi r M_r}{r^{n+1}}\\
& = \frac{n! M_r}{r^n}.
\end{align*}
$\blacksquare$
Teorema 37.1. (Teorema de Liouville.)
Sea $f:\mathbb{C} \to \mathbb{C}$ una función entera y acotada. Entonces $f$ es constante.
\begin{proof}
Dadas las hipótesis, tenemos que $f$ es analítica en todo punto del plano complejo. Sea $\zeta\in\mathbb{C}$ un punto arbitrario. De acuerdo con la desigualdad de Cauchy, para todo $n\in\mathbb{N}$ se cumple que:
\begin{equation*}
\left| f^{(n)}(\zeta)\right| \leq \frac{n! M_r}{r^n},
\end{equation*}donde $M_r=\max\limits_{z\in C(\zeta,r)}|f(z)|$.
Como $f$ es acotada, entonces existe una constante $M$ tal que $M_r \leq M$ para todo $z\in\mathbb{C}$. Entonces para $n=1$ se tiene que:
\begin{equation*}
\left| f'(\zeta)\right| \leq \frac{M}{r}.
\end{equation*}
Lo anterior se cumple para todo $r>0$, por lo que tomando el límite cuando $r\to\infty$ se sigue que:
\begin{equation*}
|f'(\zeta)| = 0 \quad \Longrightarrow \quad f'(\zeta)=0.
\end{equation*}
Dado que $\zeta\in\mathbb{C}$ es arbitrario, para todo $z\in\mathbb{C}$ se cumple que $f'(z)=0$ y como $f$ es entera, entonces, de la proposición 19.2 se sigue que $f$ es constante.
$\blacksquare$
Corolario 37.1.
Toda función no constante y entera no es acotada.
Demostración. Es inmediato del teorema de Liouville.
$\blacksquare$
Ejemplo 37.1.
La función $\operatorname{sen}(z)$ es entera y no es constante, por lo que no es acotada.
Corolario 37.2.
Sea $f:\mathbb{C} \to \mathbb{C}$ una función entera tal que $f(z)=u(x,y)+iv(x,y)$. Si $u(x,y)$ es acotada para todo $z=x+iy\in\mathbb{C}$, entonces $u(x,y)$ y $v(x,y)$ son funciones constantes.
Demostración. Dadas las hipótesis, sea $|u(x,y)|\leq M$ para todo $z=x+iy\in\mathbb{C}$. Definimos a la función:
\begin{equation*}
g(z) = e^{f(z)}.
\end{equation*}
Claramente $g$ es una función entera tal que $g(z)\neq 0$ para todo $z\in\mathbb{C}$. Por la proposición 20.2(4) tenemos que:
\begin{equation*}
\left|g(z)\right|=\left|e^{f(z)}\right| = e^{u(x,y)} \leq e^M, \quad \forall z\in\mathbb{C},
\end{equation*}es decir $g$ es una función acotada y entera, por lo que del teorema de Liouville se sigue que $g$ es una función constante y por tanto $f$ es función constante, por lo que $u(x,y)$ y $v(x,y)$ son constantes.
$\blacksquare$
Ejemplo 37.2.
Sean $f,g:\mathbb{C}\to\mathbb{C}$ dos funciones enteras, tales que $g(z)\neq 0$ y $|f(z)|\leq |g(z)|$ para todo $z\in\mathbb{C}$. Veamos que existe una constante $c\in\mathbb{C}$ tal que $f(z)=c g(z)$.
Solución. Definimos a la función:
\begin{equation*}
h(z) := \frac{f(z)}{g(z)},
\end{equation*}como $g(z)\neq 0$ para todo $z\in\mathbb{C}$, entonces $h$ está bien definida en $\mathbb{C}$ y es una función entera por ser el cociente de dos funciones enteras. Por hipótesis tenemos que:
\begin{equation*}
|h(z)| = \left| \frac{f(z)}{g(z)} \right| = \frac{|f(z)|}{|g(z)|} \leq 1, \quad \forall z \in \mathbb{C},
\end{equation*}es decir, $h$ es una función acotada y entera, por lo que del teorema de Liouville se sigue que $h(z)=c$, para algún $c\in\mathbb{C}$, entonces $f(z) = c g(z)$.
Teorema 37.2. (Teorema Fundamental del Álgebra.)
Todo polinomio complejo $p(z)$ de grado mayor o igual a $1$, tiene al menos una raíz en $\mathbb{C}$, es decir, existe $z_0\in\mathbb{C}$ tal que $p(z_0) = 0$.
Demostración. Dadas las hipótesis, procedemos por contradicción. Supongamos que:
\begin{equation*}
p(z) = c_0 + c_1 z + \cdots + c_{n-1} z^{n-1} + c_n z^n \neq 0,
\end{equation*}para todo $z\in\mathbb{C}$. Como $p$ es de grado $n\geq 1$, entonces $c_n \neq 0$ y $|c_n|>0$.
Consideremos a la función $f(z)=1/p(z)$, la cual está bien definida y es una función entera. Por la desigualdad del triángulo tenemos que:
\begin{align*}
\left|f(z)\right| & = \left|\frac{1}{p(z)}\right|\\
& = \dfrac{1}{|z|^n} \dfrac{1}{\left|\dfrac{c_0}{z^n} + \dfrac{c_1}{z^{n-1}} + \ldots + \dfrac{c_{n-2}}{z^2} + \dfrac{c_{n-1}}{z} + c_n\right|}\\
& \leq \dfrac{1}{|z|^n} \dfrac{1}{\left|\dfrac{c_0}{z^n}\right| + \left|\dfrac{c_1}{z^{n-1}}\right| + \ldots + \left|\dfrac{c_{n-2}}{z^2}\right| + \left|\dfrac{c_{n-1}}{z}\right| + |c_n|}.
\end{align*}
Notemos que:
\begin{equation*}
\left|\dfrac{c_{k}}{z^{n-k}}\right| = \dfrac{|c_{k}|}{|z^{n-k}|} = \dfrac{|c_{k}|}{|z|^{n-k}}.
\end{equation*}
Por lo que, si $n>k$, entonces:
\begin{equation*}
\lim_{|z|\to\infty} \left|\dfrac{c_{k}}{z^{n-k}}\right| = \lim_{|z|\to\infty} \dfrac{|c_{k}|}{|z|^{n-k}} =0,
\end{equation*}de donde:
\begin{equation*}
\lim_{|z|\to\infty} \left(\left|\dfrac{c_0}{z^n}\right| + \left|\dfrac{c_1}{z^{n-1}}\right| + \ldots + \left|\dfrac{c_{n-2}}{z^2}\right| + \left|\dfrac{c_{n-1}}{z}\right| + |c_n|\right) = |c_n| >0,
\end{equation*}es decir:
\begin{equation*}
\lim_{|z|\to\infty} |f(z)| = 0,
\end{equation*}entonces, para $\varepsilon=1$ existe $R\in\mathbb{R}$ tal que:
\begin{equation*}
R\leq |z| \quad \Longrightarrow \quad |f(z)| \leq 1.
\end{equation*}
Por otra parte, dado que el disco cerrado $\overline{B(0,R)}$ es un conjunto compacto y la función real:
\begin{equation*}
|f(z)|=\sqrt{u^2(x,y) + v^2(x,y)},
\end{equation*}es una función continua de las variables $x$ e $y$, entonces, proposición 10.9, $|f(\overline{B(0,R)})|$ es un conjunto compacto, es decir, cerrado y acotado, por lo que existe $K>0$ tal que:
\begin{equation*}
|f(z)|\leq K, \quad \forall z\in \overline{B(0,R)}.
\end{equation*}
Considerando lo anterior, sea $M:=\max\{K,1\}$, entonces para todo $z\in\mathbb{C}$ se cumple que $|f(z)|\leq M$, es decir, $f$ es una función acotada, por lo que del teorema de Liouville se sigue que $f$ debe ser constante, entonces $p$ es constante, lo cual es una contradicción, por lo que existe $z_0 \in \mathbb{C}$ tal que $p(z_0) = 0$.
$\blacksquare$
Corolario 37.3.
Un polinomio complejo $p(z) = c_0 + c_1 z + \cdots + c_{n-1} z^{n-1} + c_n z^n$, de grado $n\geq 1$, tiene una factorización:
\begin{equation*}
p(z) = c(z-z_1)(z-z_2)\cdots(z-z_n),
\end{equation*}donde $z_1, z_2, \ldots, z_n$ son las raíces de $p$ y $c\in\mathbb{C}$ es una constante.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Observación 37.1
Debe ser claro que raíces $z_1, z_2, \ldots, z_n$ del polinomio $p$ en el resultado anterior no necesariamente son distintas. En general, los factores de $p$ en el corolario 37.3 pueden agruparse en la forma:
\begin{equation*}
p(z) = c(z-z_1)^{n_1}(z-z_2)^{n_2}\cdots(z-z_k)^{n_k},
\end{equation*}donde $z_1, z_2, \ldots, z_k$ son raíces de $p$ distintas, $c\in\mathbb{C}$ es una constante y $n_1, n_2, \ldots, n_k$ son números naturales que indican, respectivamente, la multiplicidad de cada raíz de $p$.
Ejemplo 37.3.
El polinomio $p(z) = iz(z-1)^2(z+i)^5$ tiene a $z_1 = 0$ como una raíz simple, mientras que $z_2 = 1$ es una raíz doble o de multiplicidad $2$ y $z_3 = -i$ es una raíz de multiplicidad $5$.
Teorema 37.3. (Teorema de Morera.)
Sean $D\subset\mathbb{C}$ una región y $f:D \to \mathbb{C}$ una función continua en $D$ tal que:
\begin{equation*}
\int_{\gamma} f(z) dz = 0,
\end{equation*}para todo contorno cerrado en $D$. Entonces $f$ es analítica en $D$.
Demostración. Dadas las hipótesis, tenemos que para todo contorno cerrado $\gamma$ en $D$ se cumple que:
\begin{equation*}
\int_{\gamma} f(z) dz = 0,
\end{equation*}por lo que, proposición 35.2, existe una primitiva de $f$ en $D$, es decir, existe $F:D\to\mathbb{C}$ analítica tal que $F'(z) = f(z)$ para todo $z\in D$. Por el corolario 36.3, tenemos que $F\in C^\infty(D)$, en particular, $F^{(2)}(z)$ existe y también es analítica en $D$, pero $F^{(2)}(z) = f'(z)$ para todo $z\in D$. Por lo tanto, $f$ es analítica en $D$.
$\blacksquare$
Corolario 37.4. (Teorema de Morera generalizado.)
Sean $D\subset\mathbb{C}$ una dominio y $f:D \to \mathbb{C}$ una función continua en $D$ y analítica en $D\setminus\{z_0\}$, para algún $z_0 \in D$. Entonces $f$ es analítica en $D$.
Demostración. Se sigue del teorema integral de Cacuhy generalizado (para discos), teorema 36.4 y del teorema de Morera, por lo que los detalles se dejan como ejercicio al lector.
$\blacksquare$
Observación 37.2.
La fórmula integral de Cauchy nos dice cómo el valor $f(z_0)$ es representado por alguna integral de contorno. En particular, si elegimos al contorno de integración $\gamma$ como una circunferencia con centro en $z_0$, entonces podemos ver que el valor de $f(z_0)$ es un tipo de promedio de los valores de $f(z)$ en los puntos $z$ que están sobre dicha circunferencia.
Proposición 37.5. (Teorema del valor medio de Gauss.)
Sean $D \subset \mathbb{C}$ un dominio, $f:D\to\mathbb{C}$ una función analítica, $z_0\in D$ fijo y $r>0$ tal que $C(z_0,r) \subset D$, entonces:
\begin{equation*}
f(z_0) = \frac{1}{2\pi} \int_{0}^{2\pi} f(z_0+e^{it}) dt. \tag{37.1}
\end{equation*}
Demostración. Dadas las hipótesis, parametrizamos a $C(z_0,r)$ como $\gamma:[0,2\pi]$, dada por $\gamma(t)=z_0+re^{it}$. Por la fórmula integral de Cauchy tenemos que:
\begin{align*}
f(z_0) & = \frac{1}{2\pi i} \int_{C(z_0,r)} \frac{f(z)}{z-z_0} dz\\
& = \frac{1}{2\pi i} \int_{0}^{2\pi} \frac{f(z_0+e^{it})}{z_0 + re{it} -z_0} ire^{it} dt\\
& = \frac{1}{2\pi} \int_{0}^{2\pi} f(z_0+re^{it}) dt.
\end{align*}
$\blacksquare$
Definición 37.1. (Propiedad del valor medio.)
Sean $D\subset\mathbb{C}$ un dominio y $f:D\to\mathbb{C}$ una función analítica en $D$. Se dice que $f$ tiene la {\bf propiedad del valor medio} si para todo $z_0\in D$ y $r>0$ tal que $\overline{B}(z_0,r) \subset D$ se cumple que:
\begin{equation*}
f(z_0) = \frac{1}{2\pi} \int_{0}^{2\pi} f(z_0+e^{it}) dt.
\end{equation*}
Corolario 37.5.
Si $f(z)=u(x,y)+iv(x,y)$ es una función analítica en un dominio $D\subset\mathbb{C}$, entonces las partes real e imaginaria de $f$, es decir, las funciones reales $u(x,y)$ y $v(x,y)$ tienen la propiedad del valor medio en $D$, es decir:
\begin{equation*}
u(z_0) = \frac{1}{2\pi} \int_{0}^{2\pi} u(z_0+e^{it}) dt,
\end{equation*}
\begin{equation*}
v(z_0) = \frac{1}{2\pi} \int_{0}^{2\pi} v(z_0+e^{it}) dt.
\end{equation*}
Demostración. Es inmediata de la proposición 37.5 al tomar la parte real e imaginaria en ambos lados de la igualdad (37.1).
$\blacksquare$
Lema 37.1.
Sean $[a,b]\subset\mathbb{R}$, con $a<b$, un intervalo cerrado y $g:[a,b]\to\mathbb{R}$ una función continua en $[a,b]$ tal que $g(x)\geq 0$ para todo $x\in[a,b]$. Si:
\begin{equation*}
\int_{a}^{b} g(t) dt =0,
\end{equation*}entonces $g(x) = 0$ para todo $x\in[a,b]$.
Demostración. Dadas las hipótesis, definimos a la función:
\begin{equation*}
\varphi(x) = \int_{a}^{x} g(t) dt, \quad \forall x\in[a,b].
\end{equation*}
Por el teorema Fundamental del Cálculo es claro que $\varphi$ es una función diferenciable con derivada:
\begin{equation*}
\varphi'(x) = g(x), \quad \forall x\in[a,b].
\end{equation*}
Más aún, de las propiedades de la integral real se cumple que:
\begin{equation*}
0\leq \varphi(x) = \int_{a}^{x} g(t) dt \leq \int_{a}^{b} g(t) dt = 0,
\end{equation*}por lo que $\varphi(x)=0$ y $\varphi'(x)=0$ para todo $x\in[a,b]$, entonces $g(x) = 0$ para todo $x\in[a,b]$.
$\blacksquare$
Teorema 37.4. (Principio del módulo máximo.)
Sean $D\subset\mathbb{C}$ un dominio y $f:D\to\mathbb{C}$ una función analítica en $D$. Si existe un punto $z_0 \in D$ tal que $|f(z)|\leq |f(z_0)|$ para todo $z\in D$, es decir, el módulo $|f(z)|$ alcanza su máximo en $z_0$, entonces $f$ es una función constante en $D$.
Demostración. Dadas las hipótesis, de acuerdo con la proposición 19.3, basta probar que $|f(z)|$ es constante en $D$. Consideremos a la función $g:D\to\mathbb{R}$ dada por $g(z)=|f(z)|$. Procedemos a probar que $g$ es constante en $D$.
Notemos que, como $D$ es un dominio, en particular es abierto, por lo que para cada $z\in D$ existe un disco abierto $B(z,\rho)\subset D$. Si $0<r<\rho$, entonces $\overline{B}(z_0,r)\subset B(z_0,\rho) \subset D$. Por lo que, de la proposición 37.5 se cumple que:
\begin{equation*}
f(z) = \frac{1}{2\pi} \int_{0}^{2\pi} f(z+re^{it}) dt,
\end{equation*}de donde:
\begin{align*}
g(z) & = |f(z)|\\
& = \left|\frac{1}{2\pi} \int_{0}^{2\pi} f(z+re^{it}) dt\right|\\
& \leq \frac{1}{2\pi} \int_{0}^{2\pi} \left|f(z+re^{it}) \right| dt\\
& = \frac{1}{2\pi} \int_{0}^{2\pi} g(z+re^{it}) dt, \tag{37.2}
\end{align*}para cualquier $0<r<\rho$.
Sea $M=g(z_0) = |f(z_0)|\geq 0$ y definimos a los conjuntos:
\begin{equation*}
U:=\{z\in D : g(z) = M\}, \quad V:=\{z\in D : g(z) < M\}.
\end{equation*}
Entonces $D = U \cup V$ y $U \cap V = \emptyset$. Veamos que $V = \emptyset$. Para ello probemos que $U$ y $V$ son ambos abiertos y utilicemos el hecho de que $D$ es conexo.
Sea $z\in U$ y $\rho>0$ tal que se cumple (37.2) para $0<r<\rho$. Notemos que para $r$ fijo en este intervalo, como $z\in U$ y $g(z) \leq M$ para todo en $z\in D$, entonces se cumple que:
\begin{equation*}
M = g(z) \leq \frac{1}{2\pi} \int_{0}^{2\pi} g(z+re^{it}) dt \leq \frac{1}{2\pi} \int_{0}^{2\pi} M dt = M.
\end{equation*}
Por lo que:
\begin{equation*}
\frac{1}{2\pi} \int_{0}^{2\pi} g(z+re^{it}) dt = \frac{1}{2\pi} \int_{0}^{2\pi} M dt,
\end{equation*}es decir:
\begin{equation*}
\frac{1}{2\pi} \int_{0}^{2\pi} \left[ M – g(z+re^{it}) \right] dt = 0.
\end{equation*}
Dado que $h(t)=M-g(z+re^{it}) \geq 0$ para todo $t\in[0,2\pi]$ y $g$ es una función continua, entonces por el lema 37.1 concluimos que:
\begin{equation*}
M = g(z+re^{it}),
\end{equation*}para todo $t\in[0,2\pi]$, por lo que $z+re^{it} \in U$. Es decir, la circunferencia con centro en $z$ y radio $r$ está contenida en $U$. Como esto se cumple para todo $r\in(0,\rho)$, concluimos que el disco abierto $B(z,\rho)$ está contendio en $U$. Dado que $z$ es un punto arbitrario de $U$, entonces $U$ es un conjunto abierto.
Ahora supongamos que $z\in V$, entonces $g(z)<M$. Puesto que $g$ es una función continua en $D$, en particular lo es en $z$, por lo que para $\varepsilon=M-g(z)>0$ existe $r>0$ tal que si $\zeta\in B(z,r)$, entonces $|g(z) – g(\zeta)|<\varepsilon$. De donde:
\begin{equation*}
g(\zeta)-g(z) = |g(\zeta)|-|g(z)|\leq |g(z) – g(\zeta)|<\varepsilon,
\end{equation*}por lo que:
\begin{align*}
g(\zeta) & = g(\zeta) – g(z) + g(z)\\
& < \varepsilon + g(z)\\
& = M – g(z) + g(z)\\
& = M,
\end{align*}para cada $\zeta \in B(z,r)$. Por lo que $B(z,r) \subset V$ y como $z$ era arbitrario, entonces $V$ también es abierto.
Notemos que $U\neq \emptyset$, ya que por definición al menos el punto $z_0 \in D$ es un punto de $U$. Por lo tanto, dado que $D$ es conexo, se sigue que $V=\emptyset$, entonces $g(z) = M$ para todo $z\in D$, es decir la función $|f(z)|$ es constante en $D$, por lo que el resultado se sigue de la proposición 19.3.
$\blacksquare$
Observación 37.3.
Se puede probar el principio del módulo máximo para funciones complejas continuas que satisfacen la propiedad del valor medio. Esta es una clase más general de funciones e incluye a las funciones analíticas. Se puede consultar una prueba de este hecho en Complex variables theory and applications, de H.S. Kasana.
Reformulando el teorema 37.4, podemos decir que el módulo de una función compleja, que es analítica y no constante en un dominio $D$, no alcanza su valor máximo en $D$. El principio del módulo máximo tiene numerosas formulaciones, las siguientes son ejemplos de ellas.
Observación 37.2.
Si $D\subset\mathbb{C}$ es un dominio, denotamos a la frontera de $D$ como $\partial D$, entonces $\overline{D} = D \cup \partial D$ es un dominio cerrado y acotado en $\mathbb{C}$.
Corolario 37.6.
Sea $D\subset\mathbb{C}$ un dominio acotado en el plano complejo y $f:\overline{D}\to\mathbb{C}$ una función continua en $\overline{D}$, que es analítica en $D$. Entonces $|f(z)|$ alcanza su valor máximo en algún punto de la frontera de $D$.
Demostración. Dadas las hipótesis, como $\overline{D}$ es cerrado y acotado, entonces es un conjunto compacto, proposición 10.7, y como la función $|f|$ es continua, entonces, proposición 10.10, alcanza su máximo en algún punto de $\overline{D}$. Si $|f|$ alcanza su máximo en algún punto de $\partial D = \overline{D}\setminus D$, entonces no hay nada que probar.
Supongamos que $|f|$ alcanza su máximo en algún punto de $D$, entonces, por el principio del módulo máximo, tenemos que $f$ es una función constante en $D$, por lo que, por la continuidad de $f$, se sigue que $f$ es constante en $\overline{D}$. En tal caso, $|f|$ alcanza su valor máximo, el cual es único, en cada punto de $\partial D$.
$\blacksquare$
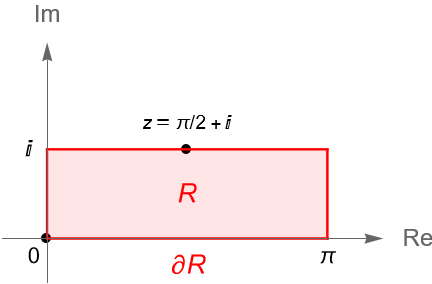
Ejemplo 37.4.
Sea $R\subset\mathbb{C}$ el dominio rectangular:
\begin{equation*}
\{z=x+iy\in\mathbb{C} : 0\leq x \leq \pi, 0\leq y \leq 1\},
\end{equation*}y sea $f(z)=\operatorname{sen}(z)$. Determinemos el valor máximo de $|f|$ en $R$.
Solución. Sabemos que $f$ es una función entera, por lo que en particular es analítica en $\operatorname{int} R$ y continua en $R$, entonces por el principio del módulo máximo sabemos que $|f|$ alcanza su máximo en $\partial R$.
Por la observación 22.5, para $z=x+iy\in\mathbb{C}$ tenemos que:
\begin{equation*}
|f(z)|=|\operatorname{sen}(z)| = \sqrt{\operatorname{sen}^2(x)+\operatorname{senh}^2(y)}.
\end{equation*}
Como $z=x+iy\in \partial R$, figura 137, entonces $\operatorname{sen}(x)$ alcanza su máximo en $\pi/2 \in [0,\pi]$, mientras que $\operatorname{senh}(y)$ alcanza su máximo en $1 \in [0,1]$, entonces el valor máximo de $|f|$ en el dominio $R$ se alcanza en $z=\pi/2+i$.
Teorema 37.5. (Principio del módulo mínimo.)
Sean $D\subset\mathbb{C}$ un dominio y $f:D\to\mathbb{C}$ una función analítica en $D$ tal que $f(z)\neq 0$ para todo $z\in D$. Si existe un punto $z_0 \in D$ tal que $|f(z_0)|\leq |f(z)|$ para todo $z\in D$, es decir, el módulo $|f(z)|$ alcanza su mínimo en $z_0$, entonces $f$ es una función constante en $D$.
Demostración. Dadas las hipótesis, como $f(z)\neq 0$ para todo $z\in D$, definimos a la función:
\begin{equation*}
g(z) = \frac{1}{f(z)},
\end{equation*} la cual es analítica en $D$. Como $|f|$ alcanza su mínimo en $z_0\in D$, entonces $|g|$ alcanza su máximo en $z_0$, por lo que, del principio del módulo máximo se sigue que $g$ es una función constante en $D$ y por tanto lo es $f$.
$\blacksquare$
Corolario 37.7.
Sea $D\subset\mathbb{C}$ un dominio acotado en el plano complejo y $f:\overline{D}\to\mathbb{C}$ una función continua en $\overline{D}$, analítica en $D$ y que cumple que $f(z)\neq 0$ para todo $z\in D$. Entonces $|f(z)|$ alcanza su valor mínimo en algún punto de la frontera de $D$.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Ejemplo 37.4.
Sea $f(z)=z^2+2$. Determinemos el valor mínmo de $|f|$ en el disco cerrado $\overline{B}(0,1)$.
Solución. Sabemos quue $f$ es una función entera, por lo que en particular es continua en $\overline{B}(0,1)$ y analítica en $B(0,1)$. Notemos que $f(z)=0$ para $z=\pm \sqrt{2}i$, los cuales son puntos fuera de $\overline{B}(0,1)$, por lo que del principio del módulo mínimo $|f|$ alcanza su valor mínimo en $\partial \overline{B}(0,1)$.
Sea $z\in \partial \overline{B}(0,1)$. Si escribimos a $z$ en su forma polar, entonces:
\begin{equation*}
z=e^{i\theta}, \quad \theta\in[0,2\pi].
\end{equation*}
Considerando la proposición 20.2 tenemos que:
\begin{align*}
|f(z)| & = |z^2+2|\\
& = |\operatorname{cos}(2\theta) + 2 + i\operatorname{sen}(2\theta)|\\
& = \sqrt{\left(\operatorname{cos}(2\theta) + 2\right)^2 + \operatorname{sen}^2(2\theta)}\\
& = \sqrt{4\operatorname{cos}(2\theta) + 5}.
\end{align*}
Determinamos los puntos críticos de $|f|$:
\begin{equation*}
\frac{d |f(z)|}{d \theta} = -\frac{8\operatorname{sen}(2\theta)}{2\sqrt{4\operatorname{cos}(2\theta) + 5}} = 0,
\end{equation*}de donde $\theta = 0, \pi/2, \pi, 3\pi/2$ son los puntos críticos de $|f|$. Entonces, en $\theta= \pi/2$ y $\theta= 3\pi/2$ la función $|f(z)|$ alcanza el valor mínimo $1$, en el disco cerrado $\overline{B}(0,1)$.
Cerraremos esta entrada con un resultado que es una aplicación del principio del módulo máximo. Aunque este resultado no es no de lo más básicos en la teoría de la Variable Compleja, nos permite ver el tipo de restricciones que la analiticidad de una función compleja impone.
Teorema 37.6. (Lema de Schwarz.)
Sea $f$ una función analítica en el disco unitario abierto $B(0,1)\subset\mathbb{C}$, tal que $|f(z)|\leq 1$ para $z\in B(0,1)$. Entonces $|f(z)|\leq |z|$ para todo $z\in B(0,1)$ y $|f'(0)|\leq 1$. Más aún, si $|f(z_0)|=|z_0|$ para algún $z_0\in B(0,1)$ tal que $z_0\neq 0$ ó $|f'(0)|=1$, entonces $f(z) = cz$ para todo $z\in B(0,1)$ y para alguna constante $c\in\mathbb{C}$ tal que $|c|= 1$.
Demostración. Dadas las hipótesis, definimos a la función $g:B(0,1)\to \mathbb{C}$ como:
\begin{equation*}
g(z) = \left\{ \begin{array}{lcc} \dfrac{f(z)}{z}, & \text{si} & z \neq 0, \\ \\ f'(0), & \text{si} & z = 0.\end{array} \right.
\end{equation*}
Notemos que $g$ es una función continua en $B(0,1)$ ya que:
\begin{equation*}
\lim_{z \to 0} g(z) = \lim_{z \to 0} \frac{f(z)}{z} = f'(0).
\end{equation*}
Por otra parte, $g$ es analítica en $B^*(0,1)=B(0,1)\setminus\{0\}$. Entonces, por el teorema de Morera generalizado, $g$ es analítica en $B(0,1)$.
Sea $0<r<1$, por lo que $\overline{B}(0,r)\subset B(0,1)$. Entonces $g$ es analítica en $\overline{B}(0,r)$ y para $z\in \partial B(0,1)$ se tiene que:
\begin{equation*}
\left|g(z)\right| = \left|\frac{f(z)}{z}\right| \leq \frac{1}{r}.
\end{equation*}
Por el principio del módulo máximo tenemos que:
\begin{equation*}
\left|g(z)\right| \leq \frac{1}{r}, \quad \forall z\in \overline{B}(0,r).
\end{equation*}
Notemos que si $z\in B(0,1)$ es fijo, al tomar el límite cuando $r\to 1$, se tiene que $|g(z)|\leq 1$, entonces $|f(z)|\leq |z|$ para todo $z\in B(0,1)$. Además $|f'(0)| = |g(0)| \leq 1$.
Por otra parte, si $|f(z_0)|=|z_0|$ para algún $z_0 \in B^*(0,1)$, entonces $|g(z_0)|=1$, es decir, el máximo del módulo de $g$ se alcanza en un punto interior del disco abierto $B(0,1)$, por lo que del principio del módulo máximo se tiene que $g$ es una función constante, es decir, $g(z) = c$, con $c\in\mathbb{C}$ tal que $|c|=1$. Del mismo modo, si $|f'(0)|=1$, entonces $|g(0)|=1$ y el máximo del módulo de $g$ se alcanza en $z=0$, por lo que del principio del módulo máximo se concluye que $g$ es constante.
$\blacksquare$
Tarea moral
- Sea $R$ el dominio rectangular $\{z:\in\mathbb{C} : |\operatorname{Re}(z)|\leq 4, |\operatorname{Im}(z)|\leq 3\}$. Supón que $f$ es una función analítica en $R$ tal que $|f(z)|\leq 1$ para todo $z\in \partial R$, entonces muestra que:
\begin{equation*}
|f'(0)| \leq \frac{14}{9\pi}.
\end{equation*} - Sea $f$ una función analítica en un dominio $D\subset\mathbb{C}$ y $z_0\in D$. Muestra que:
\begin{equation*}
f^{(n)}(z_0) = \frac{1}{2\pi r^{n+1}} \int_{0}^{2\pi} f(z_0+re^{it}) e^{-int} dt,
\end{equation*}si $\overline{B}(z_0, r) \subset D$, con $r>0$. - Muestra que:
\begin{equation*}
\int_{0}^{2\pi} \operatorname{cos}(\operatorname{cos}(t)) \operatorname{cosh}(\operatorname{sen}(t))dt =2\pi.
\end{equation*}Hint: Utiliza la proposición 37.5. - Sea $D\subset\mathbb{C}$ un dominio con frontera $\partial D$. Sea $f(z)$ una función no constante definida en $\overline{D} = D \cup \partial D$, tal que $|f(z_0)|>m$ para algún $z_0\in D$ y $|f(z)|\leq m$ para todo $z\in \partial D$. Entonces,
a) si $f$ es analítica en $D$, muestra que existe un punto en $\partial D$ donde $f$ no es continua;
b) si $f$ es continua en $\partial D$, muestra que existe un punto en $D$ donde $f$ no es analítica. - Sean $D\subset\mathbb{C}$ un dominio acotado con frontera $\partial D$ y $f(z)=u(x,y)+iv(x,y)$ una función analítica en $D$ y continua en $\partial D$. Muestra que las siguientes funciones alcanzan su máximo en la frontera del dominio $D$.
a) $(x^2+y^2)e^{u(x,y)}$.
b) $(u^2(x,y) + v^2(x,y))e^{u(x,y)}$.
c) $(\operatorname{sen}^2(x) + \operatorname{senh}^2(y))e^{u(x,y)}$.
d) $(\operatorname{cos}^2(x) + \operatorname{senh}^2(y))e^{u(x,y)}$.
Hint: En cada caso, define a la función $g(z)$ cuya parte real corresponde con la función dada y aplica el principio del módulo máximo. - Sea $f$ una función entera tal que $|f(z)|\leq c |z|^\lambda +d$ para todo $z\in \mathbb{C}$, con $\lambda, c$ y $d$ constantes positivas. Prueba que $f$ es necesariamente un polinomio complejo cuyo grado no es mayor que $\lambda$.
Hint: Modifica la prueba del teorema de Liouville. - Prueba la siguiente generalización del lema de Schwarz. Si $f$ es una función analítica en el disco $B(z_0,r)$ y $m$ es una constante tal que $|f(z)-f(z_0)|\leq m$ para todo $z\in B(z_0,r)$, entonces $|f'(z_0)| \leq m/r$ y $|f(z)-f(z_0)|\leq (m/r)|z-z_0|$ se cumple para todo $z\in B(z_0,r)$.
- Sea $f$ una función entera tal que $f(0)=0$ y $\lim\limits_{|z|\to \infty} \operatorname{Re}f(z) = 0$. Prueba que $f(z)=0$ para todo $z\in\mathbb{C}$.
Más adelante…
En esta entrada hemos abordado algunas de las consecuencias más importantes del teorema integral de Cauchy.
En la siguiente entrada veremos la versión homótopica del teorema de Cauchy y con ella generalizaremos el resultado para ciertos dominios del plano complejo $\mathbb{C}$, llamados dominios simplemente conexos, lo cual nos permitirá extender nuestra versión local, para discos, de dicho resultado.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Teorema integral de Cauchy.
- Siguiente entrada del curso: Teorema integral de Cauchy versión homótopica.