Introducción

Si queremos construir una noción más general de integración, un requisito mínimo es que se debe ajustar a la idea intuitiva de que la integral (al menos en $\mathbb{R}$) es el «área bajon la curva» de una función. Es entonces natural pensar en que primero hay que definir de manera precisa y lo más general posible conceptos como longitud, área, volúmen, y sus análogos en dimensiones más altas. Ésta es precisamente la idea de medida en $\mathbb{R}^n$. Más adelante construiremos la integral de Lebesgue sobre este concepto.

Idealmente, nos gustaría asignarle a cada subconjunto $A\subseteq \mathbb{R}^n$ algún número no negativo $\lambda (A)$ (su medida en $\mathbb{R}^n$). Para que ésta noción tenga sentido, debería satisfacer ciertas propiedades «intuitivas» y a las que ya estamos acostumbrados en dimensiones bajas. Las siguientes son deseables:

• Monotonía. Si $A\subseteq B$ son subconjuntos de $\mathbb{R}^n$, entonces $\lambda(A)\leq \lambda(B)$. Pues $B$ es «más grande» que $A$.
• Aditividad. Si $A\cap B=\emptyset$ son subconjuntos ajenos, entónces $\lambda(A\cup B)=\lambda(A)+\lambda(B)$.
• Normalización. La medida de un rectángulo generalizado, es decir un producto de intervalos $\prod_{i=1}^{n}[a_i,b_i]\subseteq\mathbb{R}^n$, debería ser el producto de las longitudes de sus lados: $\prod_{i=1}^{n}(b_i-a_i)$. Ésta idea coincide con el cálculo elemental de áreas de rectángulos y volúmenes de prismas rectangulares.

Podemos usar las ideas anteriores como punto de partida para intentar definir la medida de conjuntos más generales. El camino que seguiremos es: Tomar a los rectángulos como «unidades de medida» (simulando el punto 3) y buscar la mejor forma de aproximar un conjunto «por fuera» mediante rectángulos.

Rectángulos y su volumen.

Definición. Por intervalos (acotados) nos referimos a conjuntos no vacíos de $\mathbb{R}$ de la forma $[a,b]:=\{x\in \mathbb{R} \ : \ a\leq x \leq b \}$; $[a,b):=\{x\in \mathbb{R} \ : \ a\leq x < b \}$; $(a,b]:=\{x\in \mathbb{R} \ : \ a< x \leq b \}$; $(a,b):=\{x\in \mathbb{R} \ : \ a< x < b \}$, donde $a\leq b$ son números reales. Llamaremos a los intervalos de la forma $[a,b]$ como intervalos cerrados y a los de la forma $(a,b)$ como intervalos abiertos. Definimos la longitud $|I|$ de un intervalo $I=[a,b],[a,b),(a,b],(a,b)$ como $$|I|=b-a.$$ La longitud de un intervalo puede ser 0. A los intervalos de longitud 0 (i.e. que constan de un sólo elemento) los llamaremos «degenerados«.

Para esta parte, trabajaremos casi exclusivamente con intervalos cerrados o abiertos y acotados. Por brevedad nos referiremos a estos simplemente como intervalos.

Definición. Un rectángulo cerrado (abierto) en $\mathbb{R}^n$ es un producto cartesiano $$R:=I_1\times\ I_2\times \dots \times I_n.$$ Donde $I_1,I_2,\dots, I_n$ son intervalos cerrados (abiertos). Definimos el volúmen del rectángulo $R=I_1\times\ I_2\times \dots \times I_n$ como $$|R|=\prod_{k=1}^{n}|I_k|.$$ Si alguno de los intervalos componente de un rectángulo es degenerado, diremos también que el rectángulo es «degenerado».

Observaciones.

• Para cualquier rectángulo $R$, su volumen es no negativo (posiblemente 0) y finito: $0\leq |R| < \infty$. Un rectángulo tiene volúmen 0 si y sólo si es degenerado.
• Los intervalos cerrados/abiertos son rectángulos en $\mathbb{R}$. En este caso su volumen coincide con su longitud.
• Si $R\subseteq Q$ son rectángulos, entónces $|R|\leq |Q|$. Pues la única posibilidad es que al descomponer $R$ y $Q$ como producto de intervalos, cada intervalo en la descomposición de $R$ sea un subintervalo del correspondiente a $Q$ y la monotonía es inmediata en el caso de intervalos.
• La cerradura de un rectángulo $R$ es un rectángulo cerrado $\overline{R}$. Además $|R|=|\overline{R}|$.
• Los rectángulos cerrados son subconjuntos cerrados y acotados en $\mathbb{R}^n$ (por ende compactos). Los rectángulos abiertos son subconjuntos abiertos de $\mathbb{R}^n$. La cerradura de un rectángulo abierto es un rectángulo cerrado del mismo volúmen.
• El volúmen de un rectángulo, coincide con la noción de «medida» que nos da la integral de Riemann, a saber, la medida de Jordan: $J(R)=\int \chi_R = |R|$, donde $\int$ denota la integral de Riemann sobre algún rectángulo cerrado y no degenerado que contenga a $R$ y $\chi_R$ es la función característica de $R$.

Las siguientes propiedades del volúmen de los rectángulos nos serán útiles más adelante.

Proposición. (Aproximación por rectángulos abiertos y cerrados). Si $R$ es un rectángulo cerrado, entónces $$|R|=\inf \{|Q| \ :\ R\subseteq Q \text{ y $Q$ es un rectángulo abierto} \}.$$ Similarmente Si $R$ es abierto, entónces $$|R|=\sup \{|Q| \ :\ Q\subseteq R \text{ y $Q$ es un rectángulo cerrado}\ \}.$$

Demostración. Para el caso en el que $R=[a_1,b_1]\times [a_2,b_2]\times \dots \times [a_n,b_n]$ es cerrado, de las observaciones sabemos que $|R|\leq |Q|$ para cualquier rectángulo abierto tal que $R\subseteq Q$, de donde $$|R|\leq \inf\{|Q| :\ R\subseteq Q \text{ y $Q$ es un rectángulo abierto} \} .$$

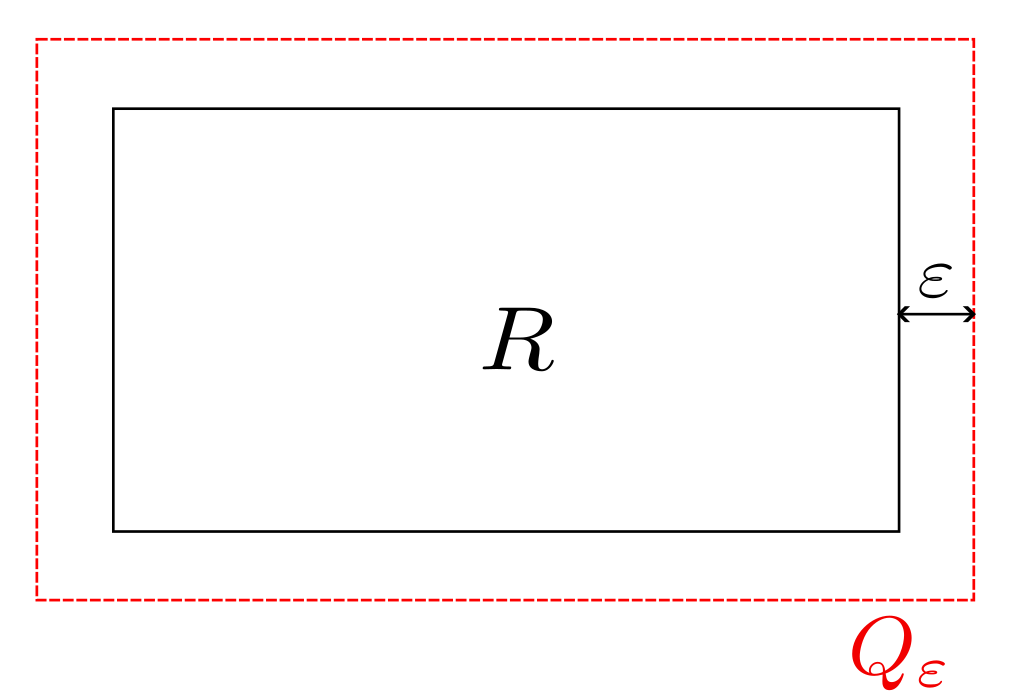
Por otro lado, al definir el rectángulo abierto $$Q_{\varepsilon}=(a_1- \varepsilon,a_1+ \varepsilon ) \times (a_2-\varepsilon,a_2+\varepsilon)\times \dots \times (a_n-\varepsilon,a_n+\varepsilon)$$

Es claro que $R\subseteq Q_{\varepsilon}$ para todo $\varepsilon>0$. Usando la definición, $|Q_{\varepsilon}|$ se puede escribir como $$\prod_{k=1}^{n}(b_k-a_k)+\varepsilon f(\varepsilon)=|R|+\varepsilon f(\varepsilon)$$ Donde $f(\varepsilon)$ es algún polinomio en $\varepsilon$. Por continuidad se sigue que $\lim_{\varepsilon \to 0^+}|Q_{\varepsilon}|=|R|$. Concluimos $$|R|\geq \inf \{|Q| \ :\ R\subseteq Q \text{ y $Q$ es un rectángulo abierto} \}.$$ El argumento para rectángulos abiertos es similar.

$\square$

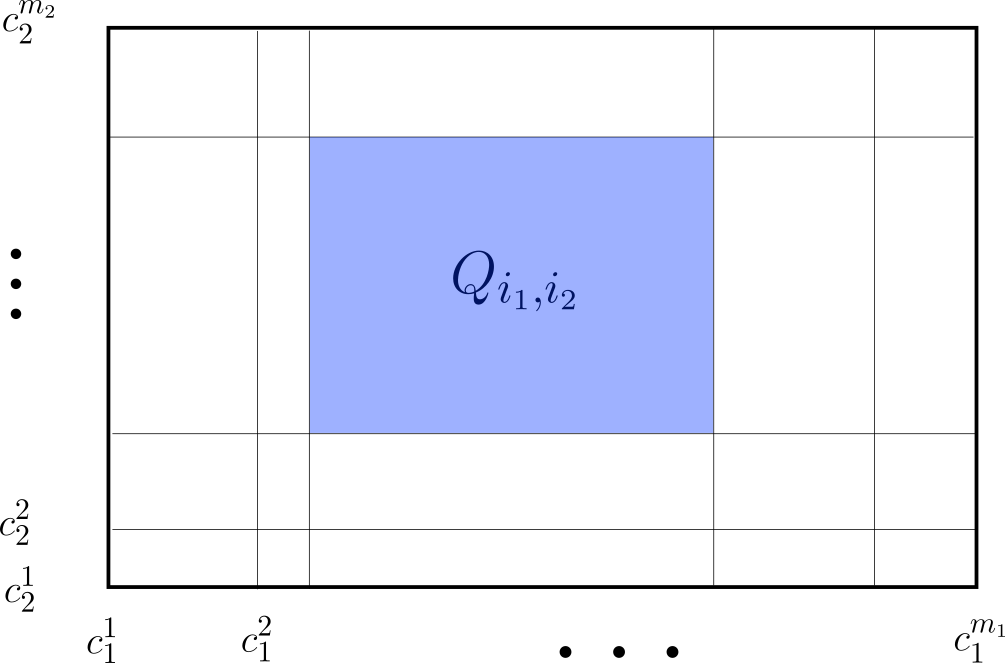
Proposición (Descomposición en subrectángulos preserva volúmen). Sea $R=[a_1,b_1]\times [a_2,b_2]\times \dots \times [a_n,b_n]$ un rectángulo cerrado y no degenerado. Supongamos que para cada $i=1,2,\dots ,n$ $$a_i=c_i^1<c_i^2<\dots <c_i^{m_i}=b_i.$$ Son puntos intermedios del intervalo $[a_i,b_i]$. Esto induce una descomposición de $R$ en subrectángulos: $$Q_{i_1,i_2,\dots, i_n}=[c_1^{i_1},c_1^{i_1+1}]\times [c_2^{i_2},c_2^{i_2+1}]\times \dots \times [c_n^{i_n},c_n^{i_n+1}].$$ Con $1\leq i_1 < m_1,1\leq i_2 < m_2, \dots ,1\leq i_n < m_n $. Entonces:
$$|R|=\sum_{i_1,i_2,\dots, i_n} |Q_{i_1,i_2,\dots, i_n}|.$$

Demostración. Denotemos por $J$ a las $n$-tuplas de la forma $(i_1,i_2,\dots, i_n)$ con $1\leq i_1 < m_1,1\leq i_2 < m_2, \dots 1\leq i_n < m_n $. Si definimos $d_k^j=(c_k^{j+1}-c_k^j)$ (los lados de los subrectangulos), tenemos que $(a_k-b_k)=\sum_{j=1}^{m_{i}-1} d_k^j$. Luego, lo anterior se reduce a probar:
$$\prod_{k=1}^{n}(b_k-a_k)=\prod_{k=1}^{n}\sum_{j=1}^{m_i-1}(d_k^j)=\sum_J \prod_{k=1}^{n}(d_k^{i_k}).$$

La ultima igualdad es inmediata por distributividad. (Para convencerte de esto, piensa que para desarrollar el producto de en medio, para cada $k$ hay que escoger un término $j=i_k$, multiplicar estos términos para obtener $d_1^{i_1}d_2^{i_2}\dots d_n^{i_n}$ y luego sumar sobre todas las posibles elecciones, que es precisamente el término derecho ).

$\square$

Proposición. Si $R$ es un rectángulo cerrado cubierto por una cantidad finita $N$ de rectángulos (cerrados o abiertos) no degenerados: $R\subseteq \bigcup_{k=1}^{N} Q_k$, entonces $$|R|\leq \sum_{k=1}^{N} |Q_k|.$$

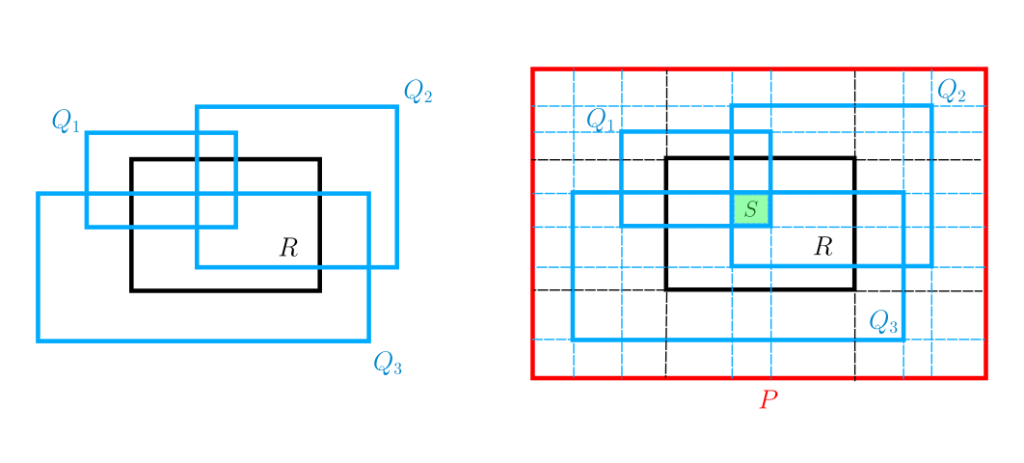
Demostración. Tomando las cerraduras de $Q_1,Q_2,\dots, Q_N$ es suficiente probarlo cuando la cubierta consta de rectángulos cerrados. Al ser una cantidad finita de rectángulos, podemos encontrar un rectángulo $P$ suficientemente grande que contenga a $R,Q_1,Q_2,\dots, Q_N$. Proyectemos los extremos de los intervalos componente de cada uno de los rectángulos $R,Q_1,Q_2,\dots, Q_N$ sobre los intervalos componente de $P$. Por construcción, esto induce descomposiciones en subrectángulos en cada uno de $P,R,Q_1,Q_2,\dots, Q_n$ (observa la figura). Denotemos todos los subrectángulos (de $P$) como $S_1,S_2,\dots, S_M$. Como $R\subseteq \bigcup_{k=1}^{N} Q_k$, cada subrectángulo $S$ de $R$ debe ser también un subrectángulo de algún $Q_k$. Luego, por la proposición anterior:
$$|R|=\sum_{S_j\subseteq R} |S_j|\leq \sum_{k=1}^{N} \sum_{S_j\subseteq Q_k} |S_j|=\sum_{k=1}^{N}|Q_k|.$$

$\square$

Proposición (Invarianza bajo traslaciones). Si $R=I_1\times I_2\times \dots \times I_n$ es un rectángulo, entonces la traslación por $v=(v_1,v_2,\dots, v_n)\in \mathbb{R}^n$, $v+R$ es un rectángulo con el mismo volumen que $R$ (Donde definimos la traslación por el vector $x\in \mathbb{R}^n$ de un conjunto $B$ como $x+B=\{x+b\ : \ b\in B \}$).

Demostración. Lo anterior se cumple para intervalos abiertos/cerrados, por ejemplo si $x\in \mathbb{R}$, $x+[a,b]=[a+x,b+x]$ y $|I|=(b-a)=((b+x)-(a-x))=|x+I|$. El otro caso es similar.

Para el caso de rectángulos, es fácil ver que $v+R=(v_1+I_1)\times (v_2+I_2)\times \dots \times (v_n+I_n)$. De donde por el caso anterior: $$|R|=\prod_{k=1}^{n}|I_k|=\prod_{k=1}^{n}|v_k+I_k|=|v+R|.$$

$\square$

Proposición (Dilataciones). Si $R=I_1\times I_2\times \dots \times I_n$ es un rectángulo, entonces la dilatación $cR$ es un rectángulo con $$|cR|=|c|^n|R|. $$ (Donde definimos la dilatación por $c\in \mathbb{R}$ de un conjunto $B$ como $cB=\{cb\ : \ b\in B \}$).

Demostración. Sin pérdida de generalidad, supongamos que $R=[a_1,b_1]\times \dots \times [a_n,b_n]$ es un rectángulo cerrado. Si $c\geq 0$, es fácil ver que $cR=[ca_1,cb_1]\times \dots \times [ca_n,cb_n]$. De modo que: $$|cR|=c(b_1-a_1)\times \dots \times c(b_n-a_n)=c^n (b_1-a_1)\times \dots \times (b_n-a_n)=c^n|R|. $$

Si $c<0$, entonces $cR=[cb_1,ca_1]\times \dots \times [cb_n,ca_n]$. Luego $$|cR|=(-c)(b_1-a_1)\times \dots \times (-c)(b_n-a_n)=|c|^n (b_1-a_1)\times \dots \times (b_n-a_n)=|c|^n|R|. $$

$\square$

Más adelante…

Definiremos nuestra primera noción de medida: La medida exterior, en la que el volúmen de rectángulos juega un papel fundamental.

Tarea moral

• Decimos que un conjunto $P\subseteq \mathbb{R}^n$ es un polígono especial si puede ser representado como una unión finita de rectángulos cerrados $R_1,R_2,\dots,R_m$: $$A=\bigcup_{k=1}^{m}R_k.$$
  • Demuestra que todo polígono especial $P$ se puede expresar como una unión finita de rectángulos cerrados y con interiores ajenos $P=\bigcup_{k=1}^{m’}Q_k$. ¿La descomposición es única?
  • Con $Q_1,Q_2,\dots,Q_{m’}$ como en el inciso anterior, definimos el volumen del polígono especial $P$ como: $$|P|=\sum_{k=1}^{m’}|Q_k|.$$ Demuestra que el volumen está bien definido, es decir, no depende de la colección de rectángulos con interiores ajenos $Q_1,Q_2,\dots,Q_{m’}$.
  • Sea $R_1,R_2,\dots, R_N$ una colección de rectángulos (no necesariamente cerrados), tales que $$P\subseteq \bigcup_{k=1}^{N}R_k.$$ Demuestra que $$|P|\leq \sum_{k=1}^{N}|R_k|.$$
  • Demuestra que si $P$ es un polígono especial, entonces $x+P$ y $cP$ son polígonos especiales para cualesquiera $x\in \mathbb{R}^n$ y $c\in \mathbb{R}$. Demuestra además que $|x+P|=|P|$ y $|cP|=|c|^n|P|$.
• Demuestra que la tercer proposición de la entrada sigue siendo cierta aún si los rectángulos son degenerados.