Introducción

En la entrada pasada presentamos el primer ejemplo de medida de probabilidad: la probabilidad geométrica. Pasaremos ahora a estudiar una medida de probabilidad con una motivación mucho más empírica.

¡Advertencia! Desde nuestro punto de vista, es muy probable que esta entrada no haga mucho sentido en este momento. Esto se debe a que no contamos con muchos resultados teóricos hasta ahora, y la justificación de este enfoque tiene que ver con las propiedades al límite de algunos conceptos que veremos más adelante. Para acabarla, ciertos aspectos más empíricos de este enfoque se justifican con definiciones y resultados que también veremos más adelante.

En consecuencia, quizás sería buena idea que regreses a esta entrada una vez que hayamos visto los conceptos mencionados. No te preocupes, nosotros colocaremos un enlace en las entradas finales para que puedas revisitar esta entrada en el futuro.

Motivación: Frecuencia relativa de un evento

En la primera entrada del curso y en la entrada sobre las medidas de probabilidad discutimos una de las ideas fundamentales más importantes de una medida de probabilidad: que califica a cada evento $A$ con un valor que representa su «frecuencia». Es decir, en una escala del $0$ al $1$, ¿qué tan frecuentemente ocurre $A$? Al ser un valor entre $0$ y $1$, puede interpretarse como una proporción. A la larga, la proporción entre el número de veces que ocurre el evento $A$ y el número total de realizaciones de un fenómeno aleatorio debería de ser $\mathbb{P}\left(A\right)$.

Una manera de definir la probabilidad de un evento $A$ sería realizar el fenómeno la mayor cantidad posible de veces, y obtener esa proporción. Esto es, si $n\in {\mathbb{N}}^{+}$ es el número de veces que repetimos el fenómeno aleatorio, y definimos $n_A$ como el número de veces que ocurrió $A$ en esas $n$ realizaciones, obtenemos la proporción mencionada, que es llamada la frecuencia relativa ($\mathrm{FrecRel}$) de $A$:

$$\mathrm{FrecRel}(A)=\frac{n_A}{n}.$$

Ahora, ¿cuál sería el valor de $n$ para afirmar que el fenómeno se repitió la mayor cantidad posible de veces? ¿1,000? ¿10,000? ¿${10}^{100}$ veces? Afortunadamente, en el mundo de las matemáticas podemos trabajar con el concepto del infinito. Por ello, en la teoría matemática, «la mayor cantidad de veces posible» de repetir el fenómeno aleatorio sería realizarlo una infinidad de veces. Así, la probabilidad frecuentista será precisamente el límite cuando $n$ tiende a infinito de la frecuencia relativa de $A$.

Definición de la probabilidad frecuentista

Tomando en cuenta la discusión anterior, presentamos la definición de la probabilidad frecuentista.

---

Definición 1.17. Sea $\mathrm{\Omega }$ el espacio muestral de algún fenómeno aleatorio, y sea $\mathcal{F}$ un σ-álgebra sobre $\mathrm{\Omega }$. Para cada $A\in \mathcal{F}$, sea $n_A$ el número de veces que ocurre el evento $A$ en $n$ realizaciones del fenómeno. Es decir, $n_A$ es el número de veces que el resultado del experimento aleatorio es alguno de los elementos de $A$. Así, se define la probabilidad frecuentista para cada $A\in \mathcal{F}$ como sigue:

$$\mathbb{P}\left(A\right)=\underset{n\to \mathrm{\infty }}{lim}\frac{n_A}{n}.$$

---

La definición de la probabilidad frecuentista está dada por un límite al infinito. Por desgracia, esto es algo que no podemos concretar en la vida real, ya que nunca terminaríamos de repetir el fenómeno aleatorio. Por ello, lo que hacemos es aproximar este límite repitiendo el fenómeno $n\in {\mathbb{N}}^{+}$ veces, con $n$ lo más grande posible (el número de veces que permitan nuestros recursos, tiempo, voluntad, etc.), y tomamos el cociente

$$\mathbb{P}\left(A\right)\approx \frac{n_A}{n}.$$

Sin embargo, ten cuidado, esta aproximación no necesariamente es precisa, y no sabemos qué tan rápido converge ese límite a un valor dado. ¡Recuerda que no importa qué tan grande sea el número de veces que repitas el experimento, ese número siempre está más cerca de $0$ que de $\mathrm{\infty }$!

Por fortuna, pese a sus limitaciones formales, este enfoque captura una idea fundamental de la probabilidad: es una medida de la frecuencia con la que ocurre un evento.

Visualización mediante el uso «simulación»

Aquí veremos una forma de visualizar la idea de este enfoque. Para ello, simularemos algunos resultados «aleatorios» utilizando un lenguaje de programación. Por el momento no haremos énfasis en cuál lenguaje de programación usamos, simplemente presentaremos los resultados. Más adelante daremos una introducción a un lenguaje de programación en el que se pueden hacer muchas cosas de probabilidad (y estadística).

En el siguiente gráfico presentamos los resultados de $n=150$ simulaciones de un experimento aleatorio cuyo espacio muestral es $\mathbb{R}$. Cada uno de los puntos en la gráfica es de la forma $(k,{\omega }_k)$, con $k\in \{1,\dots ,150\}$ y donde ${\omega }_k$ es el $k$-ésimo resultado de la simulación.

Ahora, sea $A$ el siguiente evento:

$$A=\{\omega \in \mathbb{R}\mid \omega \le -0.5\}.$$

Como mencionamos previamente, una manera de aproximar la probabilidad de $A$, desde el enfoque frecuentista, es usando la frecuencia relativa de $A$. Para ello, es necesario calcular $n_A$: el número de resultados que satisfacen $A$ dentro de $n$ simulaciones.

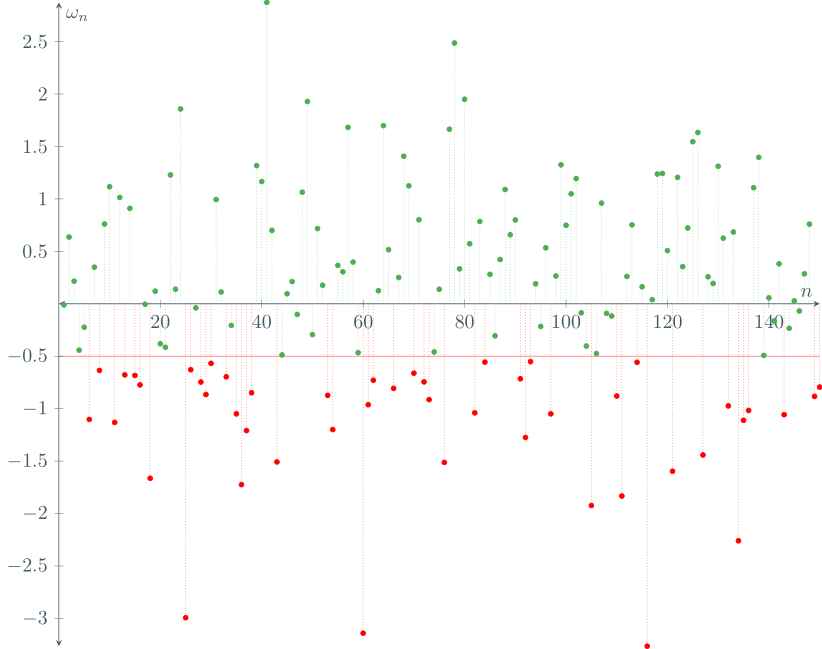
Ahora, si cuentas cuántos puntos rojos hay, notarás que son $48$. Es decir, hay $48$ observaciones en las que ocurrió $A$. Por ello, $n_A=48$. Por otro lado, ya habíamos acordado que $n=150$. Así, nuestra aproximación de la probabilidad de $A$ sería

$$\mathbb{P}\left(A\right)\approx \frac{n_A}{n}=\frac{48}{150}=0.32.$$

De hecho, observa cómo se comporta la frecuencia relativa de $A$ al incrementar el número de simulaciones:

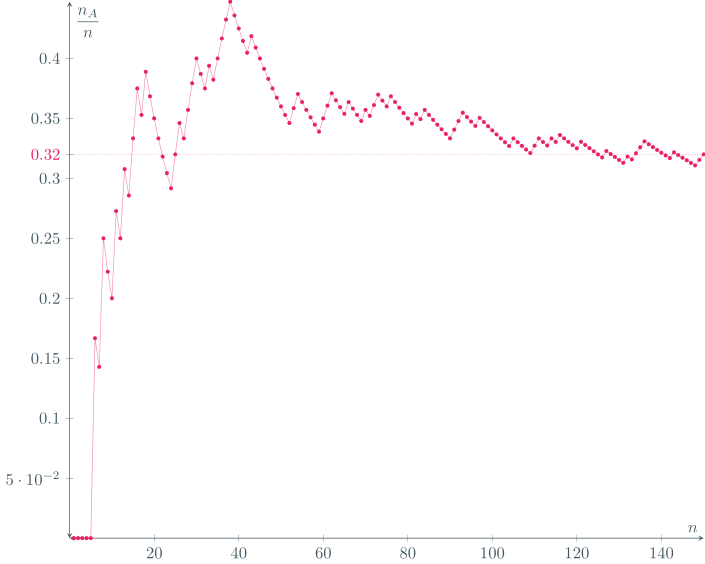
Para obtener esta última gráfica, obtuvimos $\mathrm{FrecRel}(A)$ conforme $n$ crece, hasta llegar a $n=150$. Nota cómo el valor se va estabilizando conforme crece el número de simulaciones.

De momento, esta manera de visualizar el enfoque frecuentista puede parecer «circular», pues al momento de hacer las simulaciones, es necesario darle valores a la computadora para que genere resultados siguiendo una cierta medida de probabilidad, así que el resultado es algo que ya se esperaba… En realidad, este comportamiento es consecuencia de un teorema muy importante que veremos más adelante: la ley de los grandes números.

Tarea moral

1. Argumenta por qué la probabilidad frecuentista es, efectivamente, una medida de probabilidad.
2. Para que tú puedas replicar lo visto en esta entrada, toma una moneda y lánzala muchas veces, registrando los resultados. Para el evento $A$ de que el resultado sea «águila», calcula $n_A/n$, donde $n$ es el número de lanzamientos que llevas, y $n_A$ es el número de veces que ha salido «águila».

Más adelante…

La probabilidad frecuentista es un concepto que resulta fundamental para el desarrollo de la estadística inferencial. El enfoque frecuentista es el que funciona como base para el desarrollo del contenido que se aborda en la materia de Estadística I (llamada Inferencia Estadística en el plan de estudios de la carrera de actuaría de la Facultad de Ciencias de la UNAM).

¡Muy importante! Pese a que aquí abordamos este concepto como una medida de probabilidad, hay un resultado muy importante que veremos cerca del final del curso: la ley de los grandes números. Este teorema es de suma importancia, pues da validez formal a este enfoque de la probabilidad, y en realidad hace innecesaria la definición de este enfoque, pues la teoría naturalmente admite esta interpretación. Por otro lado, más adelante daremos una introducción al lenguaje de programación que usamos para realizar las simulaciones en esta entrada.

Lo siguiente que haremos en el curso será ver el último enfoque de relevancia histórica por el momento: la probabilidad clásica. Sin embargo, para su estudio será necesario presentar varios principios de conteo. Por ende, dedicaremos unas cuantas entradas a algunos de estos principios.

Entradas relacionadas

• Ir a Probabilidad I
• Entrada anterior del curso: La Probabilidad Geométrica
• Siguiente entrada del curso: Principios de Conteo 1 – Suma y Producto