En una entrada anterior recordamos el concepto de producto interior. A continuación presentamos el concepto de norma, norma Euclidiana.
Comenzamos:
Norma
Una norma en un espacio vectorial $(V , + , \cdot )$ es una función
$$\|.\|: V \times V \longrightarrow \mathbb{R}$$ tal que:
- $\|v\| \geqslant 0 \; \; \forall \, v \in V$
- $\|v\| =0 \iff v=0 \in V$
- $\|\lambda v\| = |\lambda| \, \|v\| \; \; \forall \; v\in V ;\; \forall \; \lambda \in \mathbb{R}$
- $\|v+w\| \leqslant \|v\| + \|w\| \; \; \forall \; v, w \in V$
Norma Euclidiana en $\mathbb{R}^n$
Sea $x \in \mathbb{R}^n$ tal que $x=(x_1, x_2, \dotsc, x_n)$ se define la norma Euclidiana como:
$$\big\| x \big\|=\sqrt{x_1^2 + x_2^2 + \dotsc + x_n^2 \, \; }$$
La norma Euclidiana cumple con la desigualdad de CB.S. (Cauchy-Bunyakowski-Schwarz) y con la ley del paralelogramo.
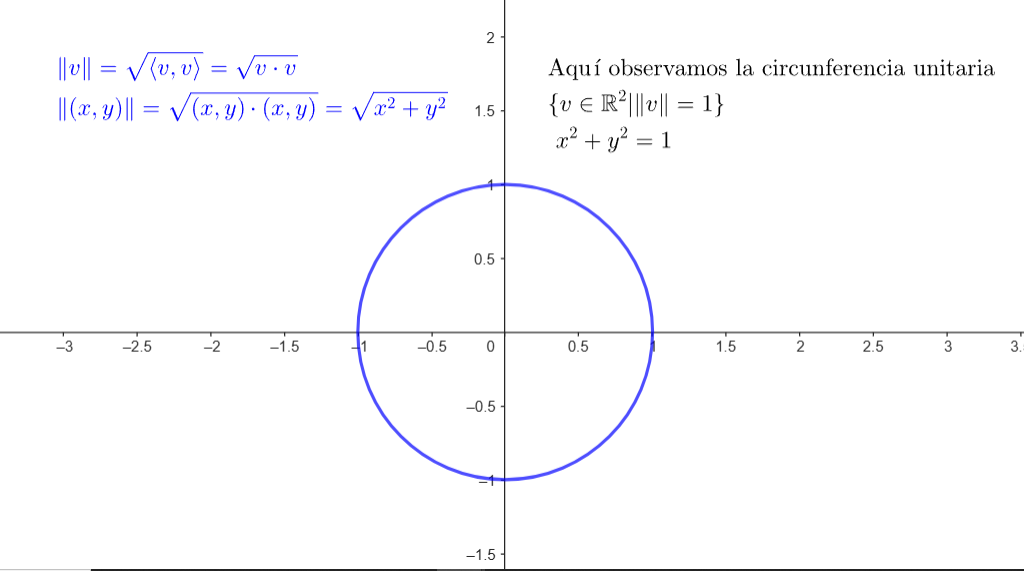
La norma Euclidiana es un ejemplo de norma inducida por un producto interior, ya que
$$\big\| v \big\|=\sqrt{v_1^2 + v_2^2 + \dotsc + v_n^2 \, \; } = \sqrt{ \langle v, v \rangle}$$
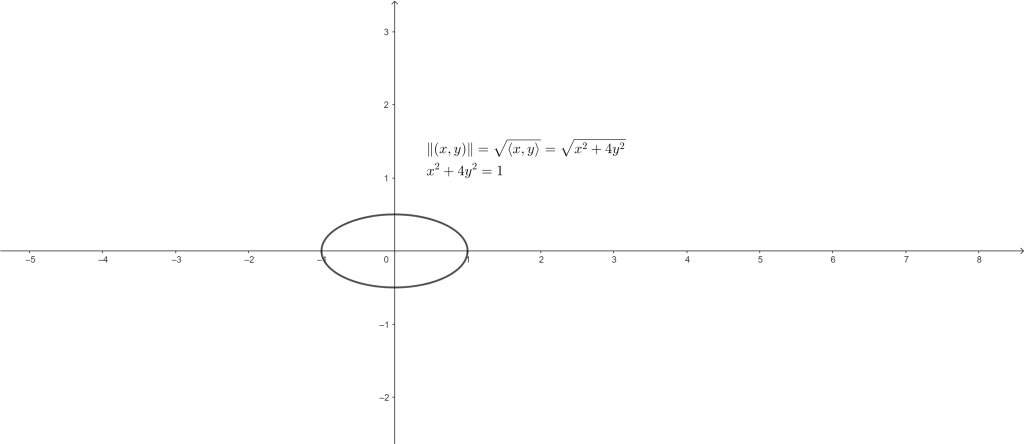
Otro ejemplo de norma inducida por otro producto interior en $\mathbb{R}^2$ se representa en la siguiente imagen