Consideremos el paralelogramo cuyos vértices son los puntos $(2,1)$,$(-1, 1)$,$(-2, -1)$,$(1, -1)$.
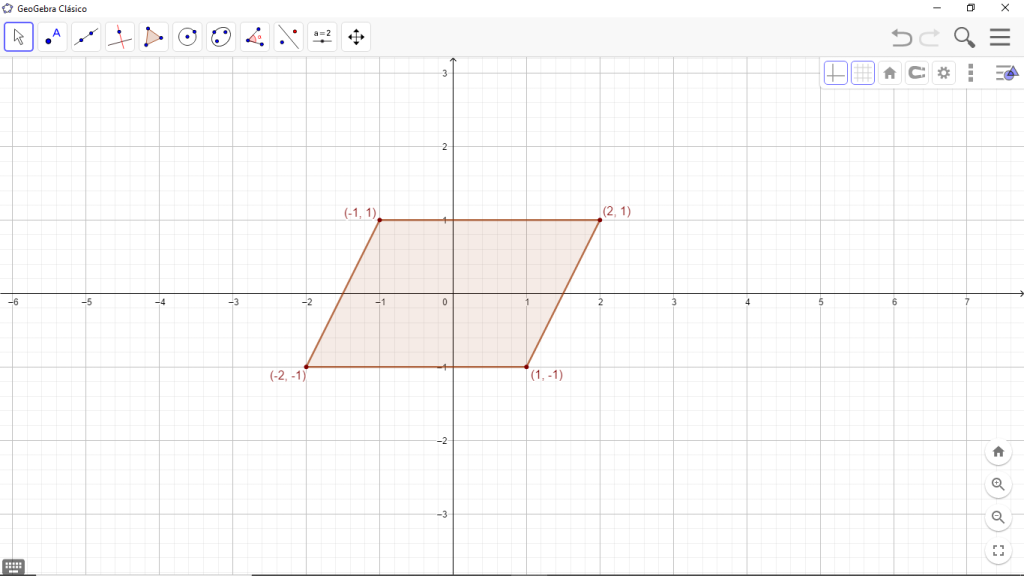
Sea $A=\{(x, y) \in \mathbb{R}^2|-1\leqslant y \leqslant 1,\; -3 \leqslant y-2x \leqslant 3 \}$
Este paralelogramo es un conjunto convexo y también simétrico respecto al origen, es decir que $$(x, y) \in A \Longrightarrow (-x, -y) \in A$$
Además es cerrado, $\bar{A}=A \cup \partial A = A$, donde $\partial A$ es la unión de los elementos de recta que forman las aristas, incluyendo los vértices.
Es acotado con la norma Euclidiana (un conjunto es acotado si está contenido en una bola).
Entonces, nos preguntamos si ¿existe una norma $\| \; \|_{\square}: \mathbb{R}^2 \longrightarrow \mathbb{R}$ tal que $A$ sea la bola unitaria cerrada?, es decir $$A=\{ (x, y) \in \mathbb{R}^2 | \|(x, y)\|_{\square} \leqslant 1\}$$
Para que la frontera sea la «circunferencia unitaria» debe suceder que si $$(x, y) \in \partial A \Longrightarrow \|(x, y)\|_{\square}=1$$
Para que sea norma se debe complir que $$\|(0, 0)\|_{\square}=0$$
y además debe cumplir que $$\|t(x, y)\|_{\square} = |t| \|(x, y)\|_{\square}$$
Analicemos que:
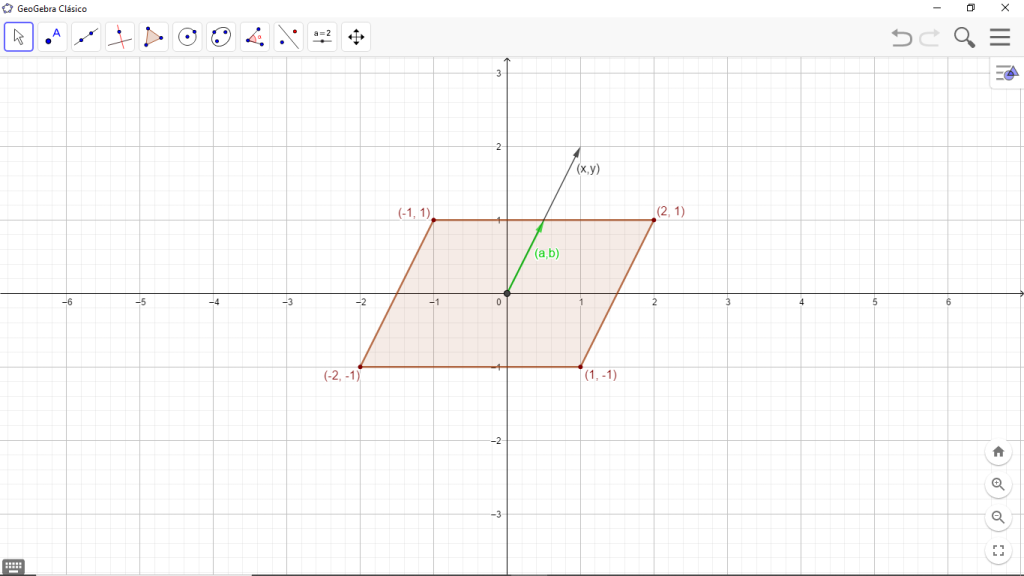
si $$(x, y) = \lambda (a, b)$$ entonces $$\| (x, y)\|_{\square} =|\lambda|\| (a, b)\|_{\square} = |\lambda|$$ ya que el punto $(a, b)$ es un punto de $A$.
Entonces ¿cuál es la regla de correspondencia que a cada $(x, y) \longrightarrow |\lambda|=\|(x, y)\|_{\square}$?
Sea $(x, y) \in \mathbb{R}^2$, tenemos que considerar los siguientes casos:
Caso «fácil»: si $(x, y)$ está en la recta diagonal.
Caso «menos fácil»: si $(x, y)$ no está en ninguna recta que contenga a una diagonal.
Pregunta auxiliar ¿cuáles son las ecuaciones de las rectas que contienen a las diagonales del paralelogramo?
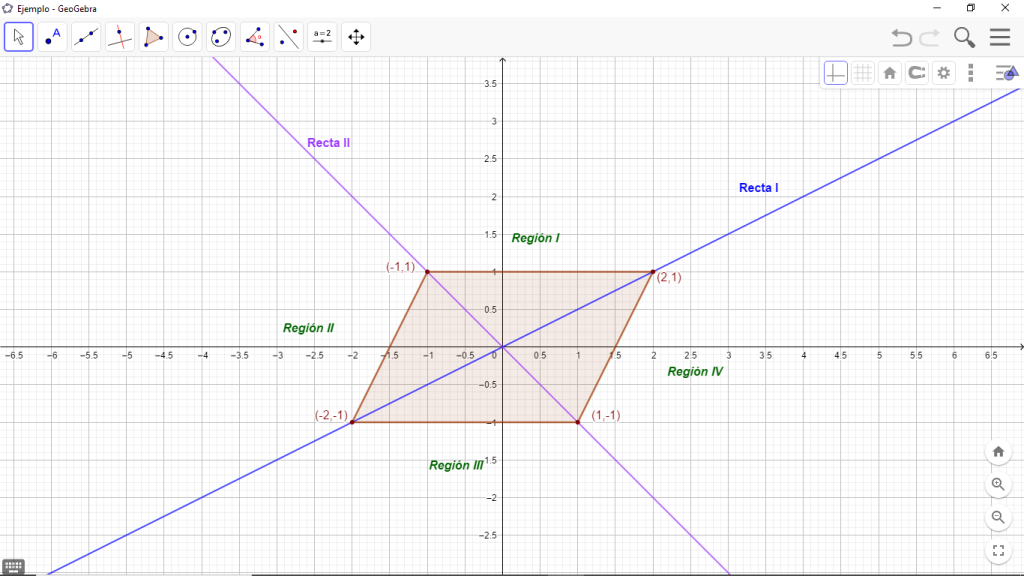
Tenemos que las ecuaciones de las rectas que contienen a las diagonales son:
Recta I: $y=\frac{1}{2}x$
Recta II: $y=-x$
Comenzamos analizando el caso «fácil»:
CASO «punto en la Recta I»: si $(x, y)=\lambda (2,1)$
entonces $(x, y) =(2\lambda , \lambda)$
por lo tanto $y = \lambda$
Ejemplo: $\|(4, 2)\|_{\square}=2$
CASO «punto en la Recta II»: si $(x, y) =\lambda (-1, 1)$
entonces $(x, y) = (-\lambda, \lambda)$
por lo que $y = \lambda$
Ejemplo: $\|(-3, 3)\|_{\square} = 3$
Análogamente se estudia el CASO III $(x, y) = \lambda (-2, -1)$ y el CASO IV, cuando $(x, y) = \lambda (1, -1)$.
Ejemplo: $\|(-10, -5)\|_{\square} =5$
$\|(8, -8)\|_{\square} = 8$
Ahora, analizamos el caso «menos fácil»:
CASO «punto en la Región I»: si $(x,y)$ está en el cono generado por los vectores $\vec{a}=(2,1)$ y $\vec{b}=(-1,1)$.
$$(x,y)=\alpha \vec{a} + \beta \vec{b} \hspace{3mm} \alpha, \beta > 0$$
Afirmación:
$t=máx \{|y|, \frac{|2x-y|}{3}\}$
Sea $(x,y) \in \mathbb{R}^2 / \partial \square$.
Consideramos 4 posibilidades, dadas por la ubicación del punto en algunas de las cuatro partes en las que queda dividido el plano, según las rectas $y=\frac{1}{2}x$ y $y=-x$.
Veamos que sucede cuando el punto está en las regiones «I» y «IV». Los dos casos restantes son análogos.
Cuando $(x,y)$ está en la Región I, cumple que: $$y>-x$$ $$y>\frac{1}{2}x$$
Observación: como $y>0$ entonces al unir $(x,y)$ con $(0,0)$ cortamos a la arista superior en un punto de la forma $(a,b)$ pero la arista superior está contenida en la recta $y=1$ por lo que $b=1$ por lo tanto $(a,b)=(a,1)$.
Luego $(x,y)=t(a,b)=t(a,1)$
Por lo tanto, $$y=t$$
$$\|(x,y)\|_\square =y$$
Cuando $(x,y)$ está en la Región IV, cumple que: $$y>-x$$ $$y<\frac{1}{2}x$$
Ahora $x>0$ por lo que al unir $(x,y)$ con $(0,0)$ cortamos a la arista del lado derecho del paralelogramos en el punto $(a,b)$, pero como la arista está contenida en la recta $y=2x-3$ tenemos que $b=2a-3$
Luego $$(x,y)=t(a,b)$$
por lo que $x=ta$ y $y=tb$ entonces $$y=t(2a-3)$$ $$y=2at-3t$$ $$a=\frac{y+3t}{2t}$$
Hemos propuesto $$\|(x,y)\|_\square := máx \{ |y|, \frac{|2x-y|}{3} \}$$
$$\| \; \|_\square : \mathbb{R}^2 \longrightarrow \mathbb{R}$$
Afirmación: $\| \; \|_\square$ es una norma.
$\|(x,y) \|_\square > 0$
$\|(x,y) \|_\square = 0 \iff (x,y) = (0,0)$
$\|(x,y) \|_\square = máx \{ |ty|, \frac{|2tx-ty|}{3} \} = |t| máx \{ |y|, \frac{|2x-y|}{3} \} = |t| \|(x,y) \|_{\square}$.
Por último probamos que satisface la desigualdad del triángulo, es decir que se cumple que: $\| u+v \|_{\square} \leqslant \|u \|_{\square} + \|v \|_{\square}$
Sean $u=(u_1, u_2)$ y $v=(v_1, v_2)$. Además $u+v =(u_1 + v_1, u_2 + v_2).$
Entonces $\|u+v \|_{\square} = máx \{ |u_2 + v_2|, \frac{2(u_1+v_1)-(u_2+v_2)}{3} \}$
Por demostrar $\| u+v \|_{\square} \leqslant \|u \|_{\square} + \|v \|_{\square}$
Si el máximo es $|u_2+v_2|$ entonces, se tiene que $$|u_2+v_2|\leqslant |u_2|+|v_2|\leqslant \|u\|_{\square} + |v\|_{\square}$$
Si el máximo es $\frac{2(u_1+v_1)-(u_2+v_2)}{3}$ entonces, $$\frac{2(u_1+v_1)-(u_2+v_2)}{3} = \frac{2u_1-u_2+2v_1-v_2}{3} \leqslant \frac{2u_1-u_2}{3} + \frac{2v_1-v_2}{3} \leqslant \|u\|_{\square} + |v\|_{\square}$$
Por lo anterior queda probado que $\| \; \|_{\square}$ es una norma.