MATERIAL EN REVISIÓN
Introducción
En las secciones pasadas probamos muchas propiedades interesantes de los conjuntos medibles y la medida de Lebesgue. Una omisión importante es ¿Qué pasa con las transformaciones rígidas? O más generalmente ¿Cómo interactua la medida de Lebesgue con las transformaciones lineales?
En dimensiones bajas estamos acostumbrados a que la longitud, el área y el volúmen sean invariantes bajo transformaciones rígidas; o que se multipliquen por «cierto factor» bajo transformaciones lineales generales. Así que es de esperar que algo similar ocurra con la medida de Lebesgue.
En esta entrada discutiremos de manera precisa cuál es la relación entre $\lambda(A)$ y $\lambda (TA)$ cuando $T$ es una matriz arbitraria.
Nuestro objetivo es probar lo siguiente:
Teorema. Sea $T\in M_{n\times n}(\mathbb{R})$ una matriz y $A\subseteq\mathbb{R}^n$. Entonces $$\lambda^*(TA)=|\det T|\lambda^*(A).$$ Si $A$ es medible entonces $TA$ es medible y $$\lambda(TA)=|\det T|\lambda(A).$$
Demostración.
Veremos primero el caso en el que $T$ es invertible.
Podemos hacer una serie de reducciones para simplificar la demostración. Considera lo siguiente.
Observación 1. Si el teorema es válido para dos matrices $T_1$ y $T_2$, entonces es válido para el producto $T_1T_2$ pues $$|\det T_1T_2|=|\det T_1||\det T_2|.$$ De donde $$\lambda^*(T_1T_2A)=|\det T_1|\lambda^*(T_2A)=|\det T_1||\det T_2|\lambda^*(A)=|\det T_1T_2|\lambda^*(A).$$ Y si $A$ es medible $\implies$ $T_2A$ es medible $\implies$ $T_1T_2A$ es medible.
Hecho 1. De tus cursos anteriores seguramente recordarás que toda matriz invertible se puede descomponer como producto de las llamadas «matrices elementales». Puedes consultarlo aquí [ENLACE]. Como un breve recordatorio, existen dos tipos de matrices elementales. En lo que sigue $k$ y $l$ denotan enteros fijos entre $1$ y $n$.
Matrices de multiplicación. Dado $c\in \mathbb{R}$, son matrices de la forma $M=[m_{ij}]$ con:
\begin{equation*} m_{ij}= \begin{cases} 1 & \text{si } i= j\neq k \\ c & \text{si } i= j= k \\ 0 & \text{si } i\neq j \end{cases} \end{equation*}
Por ejemplo cuando $k=1$:
\begin{equation*} \begin{pmatrix} c & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \end{equation*}
Observa que $|\det M|=c$, además que $ M^{-1}$ es también una matriz de multiplicación con $c$ reemplazado por $c^{-1}$. Dada una matriz $T$, $MT$ es la matriz que se obtiene de $T$ al multiplicar su $k$-ésima fila por $c$. Algo similar ocurre con $TM$ reemplazando «filas» por «columnas». Como transformación lineal, $M$ actúa multiplicando la $k$-ésima componente de un vector por $c$.
Matrices de suma. Dado $c\in \mathbb{R}$, son matrices $A=[a_{ij}]$ de la forma:
\begin{equation*} a_{ij}= \begin{cases} 1 & \text{si } i= j\neq k \\ c & \text{si } i=k, j=l \\ 0 & \text{si } i\neq j \end{cases} \end{equation*}
Por ejemplo, cuando $k=1,l=2$:
\begin{equation*} \begin{pmatrix} 1 & c & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \end{equation*}
Observa que $|\det A|=1$ y que $ A^{-1}$ es también una matriz de multiplicación con $c$ reemplazado por $-c$. Dada una matriz $T$, $AT$ es la matriz que se obtiene de $T$ al sumar $c$ veces la fila $l$ a la fila $k$. Algo similar ocurre con $TA$ reemplazando «filas» por «columnas». Como transformación lineal ésta actúa sobre un vector sumando $c$ veces la $l$-ésima entrada a su $k$-ésima entrada.
Por las observaciones anteriores, resulta que es suficiente probar el teorema para las matrices elementales, que denotaremos por $E_{n\times n}$.
Veamos ahora el siguiente Lema.
Lema. Sea $T\in M_{n\times n}(\mathbb{R})$ una matriz invertible. Sea $J$ el rectángulo semiabierto:
$$J=[0,1)\times \dots \times[0,1).$$
Sea $\rho$ el cociente: $$\rho=\frac{\lambda(TJ)}{\lambda(J)}.$$
Dado $A\subseteq \mathbb{R}^n$, entonces $$\lambda^*(TA)=\rho\lambda^*(A).$$ Si $A$ es medible, entonces $TA$ es medible y $$\lambda(TA)=\rho\lambda(A).$$
Demostración. La transformación lineal $x\to Tx$ es continua con inversa continua, por tanto un homeomorfismo. En particular transforma conjuntos abiertos en conjuntos abiertos y conjuntos compactos en conjuntos compactos.
Podemos expresar a $J$ como unión creciente de rectángulos, a saber: $$J=\bigcup_{k=1}^{\infty} [0,1-k^{-1}]\times[0,1-k^{-1}]\times \dots \times [0,1-k^{-1}].$$ Por la monotonía de la medida de Lebesgue es fácil ver que $\lambda(J)=1>0$. Aplicando $T$ (y usando que en general $f(\bigcup_{i\in I }C_i)=\bigcup_{i\in I} f(C_i)$) se sigue que: $$TJ=\bigcup_{k=1}^{\infty} T([0,1-k^{-1}]\times[0,1-k^{-1}]\times \dots \times [0,1-k^{-1}]).$$ Como $T$ es un homeomorfismo, cada $T([0,1-k^{-1}]\times[0,1-k^{-1}]\times \dots \times [0,1-k^{-1}])$ es un conjunto compacto. Entonces $TJ$ es unión numerable de conjuntos compactos por lo que en particular es medible.
Como $J$ es acotado, $TJ$ también es acotado así que su medida es finita. En todo caso, el cociente $\rho$ tiene sentido y está bien definido.
Veamos primero que el Lema se satisface para conjuntos abiertos. Considera $G$ un conjunto abierto arbitrario.
La idea es cubrir a $G$ con una cantidad numerable de «copias reescaladas» y ajenas de $J$. El procediemiento es estándar:
Primero cubrimos $\mathbb{R}^n$ con rectángulos de la forma $$[\alpha_1,\alpha_1+1)\times [\alpha_2,\alpha_2+1)\times \dots \times [\alpha_n,\alpha_n+1).$$ Donde cada $\alpha_k\in \mathbb{Z}$ es un número entero. Seleccionamos los rectángulos que están contenidos en $G$. Luego, partimos cada rectángulo no seleccionado en los $2^n$ subrectángulos que se obtienen al bisecar sus lados. Estos son de la forma $$\left[\frac{\alpha_1}{2},\frac{\alpha_1+1}{2}\right)\times \left[\frac{\alpha_2}{2},\frac{\alpha_2+1}{2}\right)\times \dots \times \left[\frac{\alpha_n}{2},\frac{\alpha_n+1}{2}\right).$$ Con $\alpha_k \in \mathbb{Z}$ enteros. De nuevo seleccionamos los rectángulos que están contenidos en $G$. Continuando con este proceso, al final nos quedamos con una colección numerable de copias reescaladas ajenas de $J$: $J_1,J_2,\dots$.
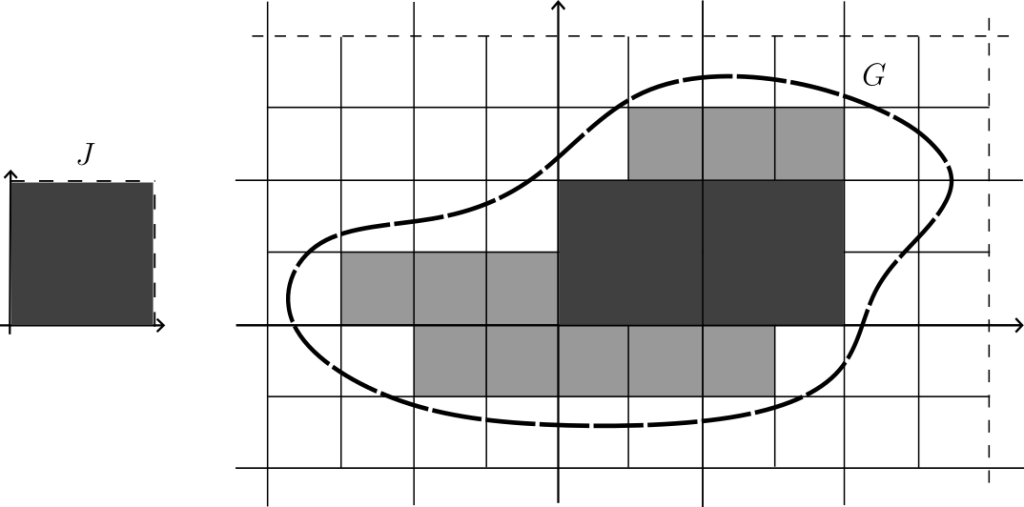
Como $G$ es abierto, para cualquier punto $x\in G$, podemos encontrar un rectángulo $R=[\frac{\alpha_1}{2^m},\frac{\alpha_1+1}{2^m})\times \dots \times [\frac{\alpha_n}{2^m},\frac{\alpha_n+1}{2^m})$ con $\alpha_1, \dots, \alpha_n \in \mathbb{Z}$ tal que $x\in R \subseteq G$. Esto garantiza que cualquier $x\in G$ es eventualmente cubierto por algún $J_k$. Además, claramente cada rectángulo $J_k$ se queda contenido en $G$. Esto nos garantiza que $$G=\bigcup_{k=1}^{\infty} J_k.$$ Es la descomposición deseada. Al aplicar $T$, se sigue también que $$TG=\bigcup_{k=1}^{\infty} TJ_k$$ Es la únión ajena de las imágenes $TJ_k$ (que son medibles).
Cada $J_k$ es una copia reescalada y trasladada de $J$, es decir, es de la forma: $$J_k=z_k+t_kJ$$ Con $z_k\in \mathbb{R}^n$, $t_k>0$. Así que podemos calcular su medida de Lebesgue: $$\lambda(J_k)=t_k^n\lambda(J)$$ $$\implies t_k^n=\frac{\lambda(J_k)}{\lambda(J)}.$$
Ahora, por linealidad se verifica fácilmente que: $$TJ_k=Tz_k+t_kTJ$$ $$\implies \lambda(TJ_k)=t_k^n\lambda(TJ).$$ Sustituyendo $t_k^n$: $$\implies \lambda(TJ_k)=\left( \frac{\lambda(J_k)}{\lambda(J)} \right)\lambda(TJ)=\rho\lambda(J_k).$$
Finalmente, por la aditividad contable:
\begin{align*}
\lambda(TG) =& \lambda\left(\bigcup_{k=1}^{\infty} TJ_k\right) \\
&= \sum_{k=1}^{\infty} \lambda (TJ_k) \\
&= \rho \sum_{k=1}^{\infty} \lambda (J_k) \\
&= \rho \lambda\left( \bigcup_{k=1}^{\infty} J_k \right) \\
&= \rho \lambda(G).
\end{align*}
Esto establece el Lema para el caso de conjuntos abiertos. Si $A\subseteq \mathbb{R}^n$ es un subconunto arbitrario, por la aproximación con abiertos de la medida exterior tenemos:
\begin{align*}
\lambda^*(TA) &= \inf_{TA\subseteq U \text{ abto.}}\{ \lambda(U) \}\\
&= \inf_{A\subseteq U \text{ abto.}}\{ \lambda(TU) \} \\
&= \inf_{A\subseteq U \text{ abto.}}\{ \rho \lambda(U) \} \\
&= \rho \inf_{A\subseteq U \text{ abto.}}\{ \lambda(U) \} \\
&= \rho \lambda^*(A).
\end{align*}
En la segunda igualdad usamos que $T$ es un homeomorfismo.
Finalmente, si $A$ es medible, para cualquier $\varepsilon>0$ podemos encontrar un abierto $U$ tal que $A\subseteq U$ y $$\lambda^*(U\setminus A)<\frac{\varepsilon}{\rho}$$ Entonces $TU$ es un abierto con
$$\lambda^*(TU\setminus TA)=\lambda^*(T(U\setminus A))=\rho \lambda^*(U\setminus A)<\varepsilon.$$
Se sigue que $TA$ es medible y $\lambda(TA)=\lambda^*(TA)=\rho \lambda^*(A)=\rho \lambda(A)$.
$\square$
El Lema anterior nos dice en particular que cuando $T$ es una matriz elemental, existe alguna constante $\rho$ tal que $$\lambda^*(TA)=\rho \lambda^*(A).$$ para cualquier $A\subseteq \mathbb{R}^n$. Queremos probar que $\rho=|\det T|$, para ello es suficiente exhibir algún conjunto particular $A$ (medible, de medida finita y no nula) para el cual podamos calcular $\rho=\frac{\lambda(TA)}{\lambda(A)}$. Tratamos los dos tipos de matrices elementales por separado.
- $T$ es matriz de multiplicación. Asumamos sin pérdida de generalidad que $T=[t_{ij}]$ con $t_{11}=c$, $t_{ii}=1$ para $i\neq 1$. En este caso $\det T=c$ (los demás casos son análogos). Escojamos $$A=[0,1]\times[0,1]\times \dots \times [0,1] \ \implies \ \lambda(A)=1$$ Si $c>0$ entonces $$TA=[0,c]\times[0,1]\times \dots \times [0,1]\ \implies \ \lambda(TA)=c$$ Y si $c<0$ entonces $$TA=[c,0]\times[0,1]\times \dots \times [0,1]\ \implies \ \lambda(TA)=-c$$ En todo caso
$$\rho=\frac{\lambda(TA)}{\lambda(A)}=|c|=|\det T|.$$ - $T$ es matriz de adición. Nuevamente, por simplicidad asumiremos que $T$ es de la forma
\begin{equation*} T=\begin{pmatrix} 1 & c & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \end{equation*}
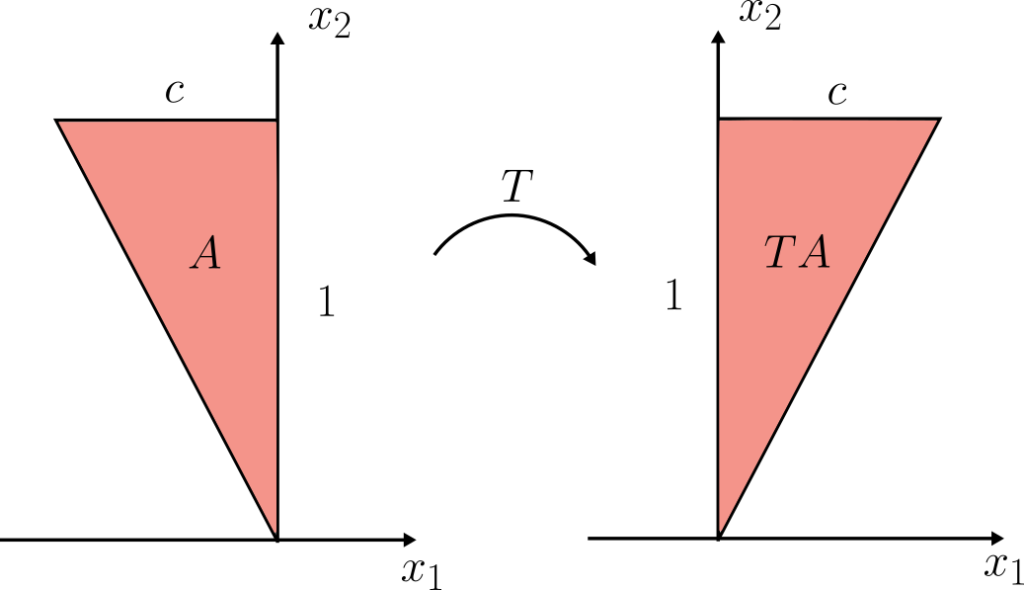
Y que $c>0$. Los demás casos son completamente análogos. Ahora, escojamos $$A=\{x\in \mathbb{R}^n \ : \ -cx_2\leq x_1\leq 0, 0\leq x_2 \leq 1, \dots, 0\leq x_n \leq 1\}.$$ Es fácil ver que $$TA=\{x\in \mathbb{R}^n \ : \ 0\leq x_1\leq cx_2, 0\leq x_2 \leq 1, \dots, 0\leq x_n \leq 1\}.$$ Si $M$ es la matriz de multiplicación
\begin{equation*} M=\begin{pmatrix} -1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \end{equation*}
Para este $A$ en particular tenemos que $$TA=MA.$$ Así que por el caso anterior tenemos $$\lambda(TA)=\lambda(MA)=|\det M|\lambda(A)=\lambda(A).$$ De donde $$\rho=\frac{\lambda(TA)}{\lambda(A)}=1=|\det T|.$$
Esto concluye la prueba para matrices elementales y por tanto, para todas las matrices invertibles. Veamos ahora el caso degenerado en el que $\det T=0$. En este caso es suficiente probar que directamente $\lambda(T\mathbb{R}^n)=0$.
Si $\det T =0$, los vectores columna de la matriz $T$ son linealmente dependientes, por lo que generan el subespacio $T\mathbb{R}^n$ de dimensión $m<n$. Por Gram-Schmidt, podemos escojer una base ortonormal $B=\{b_1,b_2,\dots,b_n \}$ de $\mathbb{R}^n$ tal que $\{ b_1,b_2,\dots, b_m \}$ sean base de $S$.
Sea entonces $M$ la matriz cuyos vectores columna son $b_1,b_2,\dots b_n$ en ese órden (ésta es ortogonal, y por tanto $|\det M|=1$). $M$ transforma la base usual de $\mathbb{R}^n$ en la base $B$, i.e. $Me_i=b_i$ (donde $e_i$ es el vector con $i$-ésima entrada 1 y las demás 0). Se sigue que: $$M(\mathbb{R}^m\times\{ 0\}^{n-m})=T\mathbb{R}^n.$$ Entonces, usando el caso no degenerado tenemos:
\begin{align*}
\lambda(T\mathbb{R}^n) &= \lambda(M(\mathbb{R}^m\times\{ 0\}^{n-m})) \\
&= |\det M|\lambda(\mathbb{R}^m\times\{ 0\}^{n-m}) \\
&\leq \lambda(\mathbb{R}^{n-1}\times\{ 0\}) \\
&= 0.
\end{align*}
Pues ya sabemos que el hiperplano $\mathbb{R}^{n-1}\times\{ 0\}$ tiene medida cero.
$\square$
Más adelante…
Definiremos el concepto de sigma-álgebra y funciones medibles, las estructuras abstractas sobre las que podemos definir la integral de Lebesgue y otros conceptos de integración más generales.