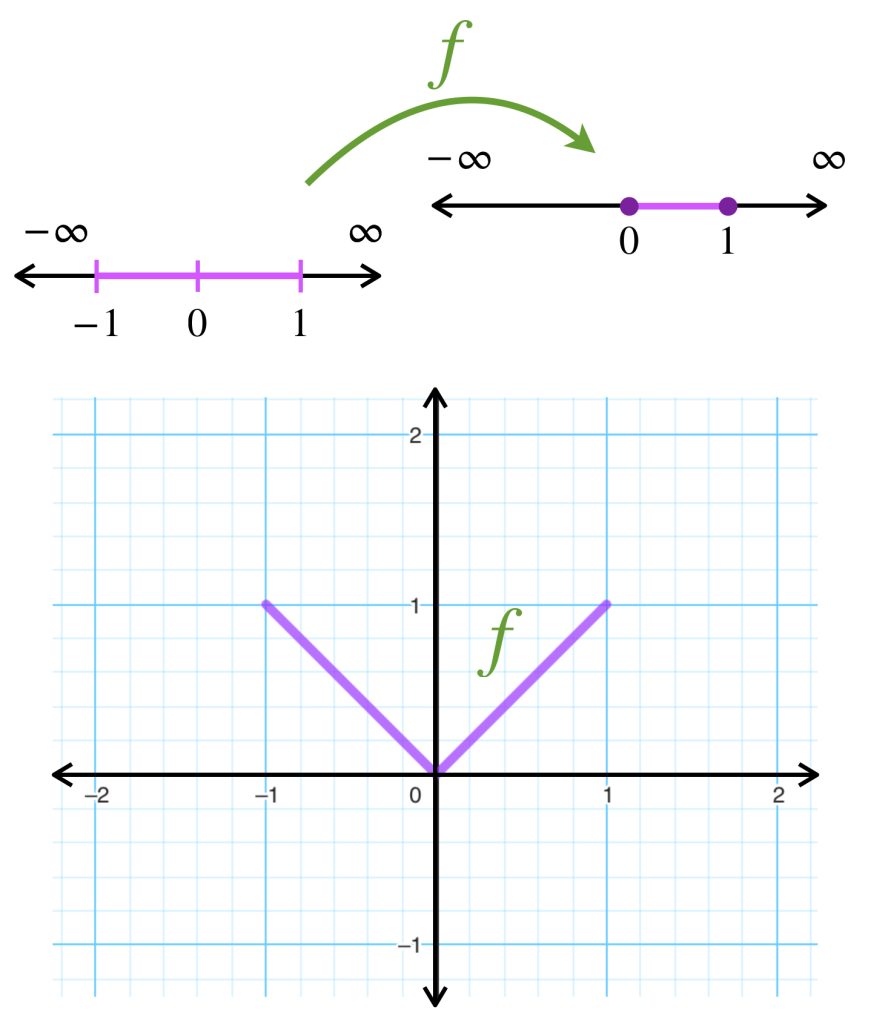
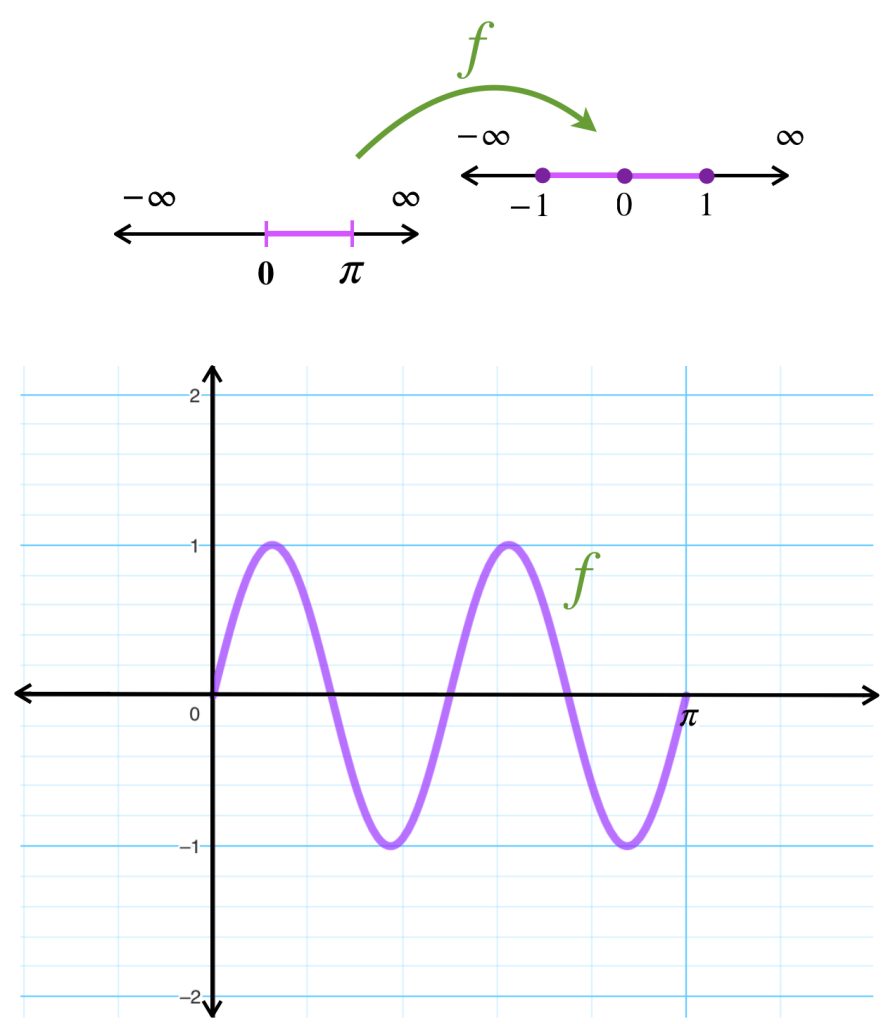
Introduccion
El Teorema de la función implicita versión para funciones $f:\mathbb{R}\rightarrow\mathbb{R}$
Teorema 1. Considere la función $y=f(x)$. Sea $(x_{0},y_{0}) \in
\mathbb{R}^{2}$ un punto tal que $F(x_{0},y_{0})=0$. Suponga que la función $F$ tiene derivadas parciales continuas en alguna bola con centro $(x_{0},y_{0})$ y que $\displaystyle \frac{\partial F}{\partial y}(x_{0},y_{0})\neq 0$. Entonces $F(x,y)=0$ se puede resolver para $y$ en términos de $x$ y definir así una función $y=f(x)$ con dominio en una vecindad de $(x_{0},y_{0})$, tal que $y_{0}=f(x_{0})$, lo cual tiene derivadas continuas en $\mathcal{V}$ que pueden calcularse como $y’=f'(x)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial x}(x,y)}{\displaystyle \frac{\partial F}{\partial y}(x,y)}$, $x \in \mathcal{V}$.
Demostración. Como $\displaystyle{\frac{\partial
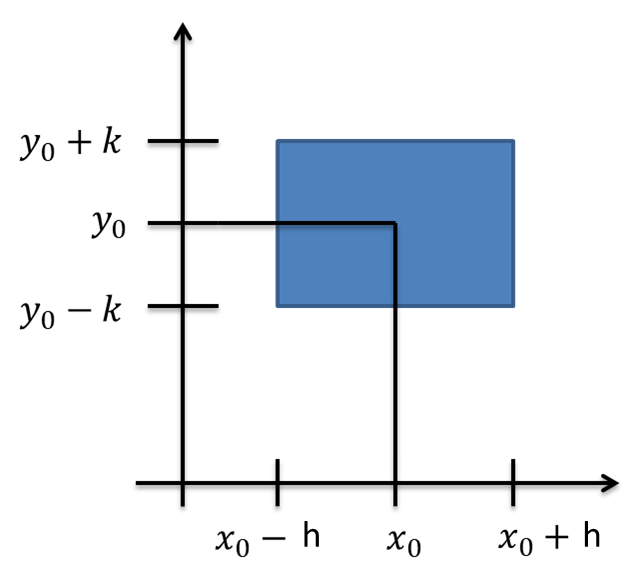
F}{\partial y}(x_{0},y_{0})\neq 0}$ supongamos sin perdida de generalidad que $\displaystyle{\frac{\partial F}{\partial y}(x_{0},y_{0})> 0}$. Por ser $\displaystyle{\frac{\partial F}{\partial y}}$ continua en una vecindad de $(x_{0},y_{0})$ entonces exite un cuadrado S, centrado en $(x_{0},y_{0})$ totalmente contenido en esa vecindad, en donde $\displaystyle{\frac{\partial F}{\partial y}(x,y)> 0}$ $\forall~x,y\in S$.Sea
$$S=\left\{(x,y)\in\mathbb{R}^{2}~|~|x-x_{0}|<h~y~|y-y_{0}|<k \right\}$$
En todo punto $(x,y)$ que pertenece a $S$, $\displaystyle{\frac{\partial F}{\partial y}(x,y)>0}$. Esto quiere decir que en $S$, $F$ es creciente y fijando $x_{0}$ en $[x_{0}-h,x_{0}+h]$ se tiene que $F$ es creciente en $[y_{0}-k,y_{0}+k]$ y se anula en $y_{0}$, por lo que
$$F(x_{0},y_{0}-k)<0~~yF(x_{0},y_{0}+k)>0$$ Consideremos ahora el par de funciones $F(x,y_{0}-k)$ y $F(x,y_{0}+k)$ definidas en el intervalo $(x_{0}-k,x_{0}+k)$. Donde ambas funciones solo tienen x como variable. La primera función cumple $F(x_{0},y_{0}-k)<0$ y por ser continua en $x_{0}$, es negativa en toda una vecindad $(x_{0}-h_{1}x_{0}+h_{1})$ de $x_{0}$. Análogamente, la segunda función cumple $F(x_{0},y_{0}+k)>0$ y por ser continua en $x_{0}$, es positiva en toda una vecindad $(x_{0}-h_{2}x_{0}+h_{2})$ de $x_{0}$. Sea $h=\min{h_{1},h_{2}}$. Entonces para toda $x$ tal que $|x-x_{0}|~y~F(x,y_{0}+k)>0$ Fijemos $x$ en el intervalo $(x_{0}-h,x_{0}+h)$, y consideremos a $F(x,y)$, sólo como función de $y$, sobre $[y_{0}-k,y_{0}+k]$. Esta función cumple que
$$F(x,y_{0}-k)<0~y~F(x,y_{0}+k)>0$$
por lo tanto según el teorema del valor intermedio, existe un único y en $(y_{0}-k,y_{0}+k)$ tal que $F(x,y)=0$. Así queda establecida la existencia y unicidad de la función $y=f(x)$. Donde además, $y_{0}=f(x_{0})$, y para todo $x\in(x_{0}-h,x_{0}+h)$ $$F(x,f(x))=0,y~~\frac{\partial F}{\partial y}(x_{0},y_{0})\neq 0$$
Vamos a comprobar que la función es continua, para ello se tiene
$$x\in[x_{0}-h,x_{0}+h]~\Rightarrow~|x-x_{0}|<h$$
tomando $h<\delta$ se tiene
$$|x-x_{0}|<\delta$$
esto quiere decir que
$$|y-y_{0}|<k$$ es decir$$|f(x)-f(x_{0})|,\frac{\partial F}{\partial y}(x_{0},y_{0})$$
existen y son continuas entonces $F$ es diferenciable por lo que
$$F(x_{0}+h,y_{0}+k)-F(x_{0},y_{0})=\frac{\partial F}{\partial x}(x_{0},y_{0})h+\frac{\partial F}{\partial y}(x_{0},y_{0})k+R(h,k)$$
Tenemos que $F$ es continua por lo que
$$F(x_{0}+h,y_{0}+k)-F(x_{0},y_{0})=0sih,k\rightarrow 0$$
también
$$R(h,k)\rightarrow 0sih,k\rightarrow 0$$
por lo que
$$\frac{\partial F}{\partial x}(x_{0},y_{0})h+\frac{\partial F}{\partial y}(x_{0},y_{0})k=0$$
esto es
$$\frac{k}{h}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0})}{\frac{\partial F}{\partial y}(x_{0},y_{0})}$$
y cuando $h,k\rightarrow 0$ se tiene
$$\frac{dy}{dx}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0})}{\frac{\partial F}{\partial y}(x_{0},y_{0})}$$
Importante: Este es un resultado que garantiza la
existencia de una función $y=f(x)$ definida implícitamente por
$F(x,y)=0$. Esto es, puede resolverse para $y$ en términos de $x$,
pero no nos dice como hacer el despeje.
Ejemplo. Considere la función $F(x,y)=e^{2y+x}+\sin(x^{2}+y)-1$ en el punto (0,0) tenemos $F(0,0)=0$. Las derivadas parciales de $F$ son
$F_{x}=e^{2y+x}+2x\cos(x^{2}+y)$
$F_{y}=2e^{2y+x}+\cos(x^{2}+y)$
que son siempre continuas. Además, $\displaystyle \frac{\partial F}{\partial y}(0,0)=3\neq0$ de modo que $\textbf{T.F.Im.}$ garantiza una vecindad de $x=0$ en la cual podemos definir una función $y=f(x)$ tal que $F(x,f(x))=0$. Obsérvese que en este caso no podemos hacer explícita la función $y=f(x)$ sin embargo tal función existe y su derivada es
$y’=f'(x)=\displaystyle -\frac{\displaystyle \frac{\partial F}{\partial x}}{\displaystyle \frac{\partial F}{\partial y}}=\displaystyle \frac{e^{2y+x}+2x\cos(x^{2}+y)}{2e^{2y+x}+\cos(x^{2}+y)}$
Ejemplo. Considere $F(x,y)=x^{4}-e^{xy^{3}-1}$ en el punto (1,1) $F(1,1)=1-1=0$, $F_{x}=4x^{3}-y^{3}e^{xy^{3}-1}$ Por lo tanto, $F_{x}|{(1,1)}=3$, $F{y}=-3xye^{xy^{3}-1}$
Y así, $F_{y}|_{(1,1)}=-3$, y $\displaystyle \frac{\partial F}{\partial y}=-3\neq0$.
El $\textbf{T.F.Im.}$ nos garantiza que en los alrededores de (1,1) el nivel cero de $F$ se ve como la gráfica de la función $y=f(x)$ y que su derivada es $y’=\displaystyle
\frac{-4x^{3}-y^{3}e^{xy^{3}-1}}{-3xy^{2}e^{xy^{3}-1}}$.
Observe que en este caso la función $F$ permite hacer el despeje en términos de $x$.
$F(x,y)=x^{4}-e^{xy^{3}-1}=0$
$x^{4}=e^{xy^{3}-1}$
$\ln (x^{4})=xy^{3}-1$
$\left(\displaystyle \frac{\ln (x^{4})+1}{x}\right)^{\frac{1}{3}}=y=f(x)$ que al derivar se debe de llegar al mismo resultado.
Ejemplo. Considere $F(x,y)=x^{2}-y^{3}-1$ en el punto $(x_{0},y_{0})$ con $y_{0}\neq 0$ tal que $F(x_{0},y_{0})=0$, $F_{x}=2x,~~F_{y}=2y$
Por lo tanto, $F_{x}|{(x{0},y_{0})}=2x_{0}$,
Y así, $F_{y}|{(x{0},y_{0})}=2y_{0}$, y $\displaystyle \frac{\partial F}{\partial y}=2y_{0}\neq0$.
El $\textbf{T.F.Im.}$ nos garantiza que en los alrededores de $(x_{0},y_{0})$ el
nivel cero de $F$ se ve como la gráfica de la función $y=f(x)$ y que su derivada es
$$y'(x)=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0})}{\frac{\partial F}{\partial y}(x_{0},y_{0})}$$
en este caso
$$y'(x)=-\frac{2x_{0}}{2y_{0}}=-\frac{x_{0}}{y_{0}}$$
si $y_{0}>0$ tal función es $f(x)=\sqrt{1-x^{2}}$ por lo que
$$y’=-\frac{x}{\sqrt{1-x^{2}}}=-\frac{x}{y}$$
si $y_{0}<0$ tal función es $f(x)=-\sqrt{1-x^{2}}$ por lo que
$$y’=-\frac{-x}{-\sqrt{1-x^{2}}}=-\frac{x}{y}$$
El Teorema de la función implicita versión para funciones $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$
Considere la función $F(x,y,z)$. Sea $(x_{0},y_{0},z_{0}) \in \mathbb{R}^{3}$ un punto tal que $F(x_{0},y_{0},z_{0})=0$. Suponga que la función $F$ tiene derivadas parciales $\displaystyle{\frac{\partial F}{\partial x},~\frac{\partial F}{\partial y},~\frac{\partial F}{\partial z}}$ continuas en alguna bola con centro $(x_{0},y_{0},z_{0})$ y que $\displaystyle \frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\neq 0$.
Entonces $F(x,y,z)=0$ se puede resolver para $z$ en términos de $x,y$ y definir así una función $z=f(x,y)$ con dominio en una vecindad de
$(x_{0},y_{0},z_{0})$, tal que $z_{0}=f(x_{0},y_{0})$, lo cual tiene derivadas continuas
en $\mathcal{V}$ que pueden calcularse como $$\frac{d z}{dx}(x,y)=-\displaystyle
\frac{\displaystyle \frac{\partial F}{\partial x}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}~~~\frac{d z}{dy}(x,y)=-\displaystyle \frac{\displaystyle \frac{\partial F}{\partial
y}(x,y)}{\displaystyle \frac{\partial F}{\partial z}(x,y)}$$
$\textbf{Importante:}$ Este es un resultado que garantiza la existencia de una función $z=f(x,y)$ definida implícitamente por $F(x,y,z)=0$. Esto es, puede resolverse para $z$ en términos de $x,y$, pero no nos dice como hacer el despeje.
Demostración. Consideremos el par de funciones
$$F(x,y,z_{0}-\ell)yF(x,y,z_{0}+\ell)$$
definidas para $(x,y)\in[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]$\La primera satisface
$$F(x_{0},y_{0},z_{0}-\ell)<0$$ la segunda cumple $$F(x_{0},y_{0},z_{0}+\ell)>0$$
Fijemos $(x,y)$ en $[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]$ y consideramos $F(x,y,z)$ solo como función de z, sobre $[z_{0}-\ell,z_{0}+\ell]$. Esta función cumple
$$F(x,y,z_{0}-\ell)<0~y~F(x,y,z_{0}+\ell)>0$$
por lo que al aplicar el Teorema del valor intermedio, obteniendose un único z en $(z_{0}-\ell,z_{0}+\ell)$ en donde $F(x,y,z)=0$.Queda así establecida la existencia y unicidad de la función $z=f(x,y)$ con dominio $[x_{0}-h,x_{0}+h]\times [y_{0}-k,y_{0}+k]$ y rango $[z_{0}-\ell,z_{0}+\ell]$ Vamos a probar que dicha f es continua, para ello si
$$\left(\begin{matrix}x\in [x_{0}-h,y_{0}+h] , y\in [y_{0}-k,y_{0}+k] \end{matrix}\right)~\Rightarrow~\left(\begin{matrix}|x-x_{0}|<h\|y-y_{0}|<k\end{matrix}\right)$$
por lo que
$$|(x,y)-(x_{0},y_{0})|<|x-x_{0}|+|y-y_{0}|<h+k$$
si $h<k$
$$|(x,y)-(x_{0},y_{0})|<2k=\delta$$
donde
$$|f(x,y)-f(x_{0},y_{0})|=|z-z_{0}|<\ell=\epsilon$$
por lo tanto $f(x,y)$ es continua.Ahora si suponemos que $\displaystyle{\frac{\partial F}{\partial x},~\frac{\partial F}{\partial y}},~\frac{\partial F}{\partial z}$ son continuas en los alrededores de $(x_{0},y_{0},z_{0})$ en tonces F es diferenciable y se tiene
$$F(x_{0}+h,y_{0},z_{0}+\ell)-F(x_{0},y_{0},z_{0})=\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})h+\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})0+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell+R(h,k,\ell)$$
De donde
$$F(x_{0}+h,y_{0},z_{0}+\ell)-F(x_{0},y_{0},z_{0})\rightarrow 0$$
$$R(h,k,\ell)\rightarrow 0$$
por lo que
$$\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})h+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell=0$$
$$~\Rightarrow~\frac{h}{\ell}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$
y cuando $h,\ell\rightarrow 0$ se tiene
$$\frac{dz}{dx}=-\frac{\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$
Análogamente
$$F(x_{0},y_{0}+k,z_{0}+\ell)-F(x_{0},y_{0},z_{0})=\frac{\partial F}{\partial x}(x_{0},y_{0},z_{0})0+\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})k+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell+R(h,k,\ell)$$
De donde
$$F(x_{0},y_{0}+k,z_{0}+\ell)-F(x_{0},y_{0},z_{0})\rightarrow 0$$
$$R(h,k,\ell)\rightarrow 0$$
por lo que
$$\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})k+\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})\ell=0$$
$$~\Rightarrow~\frac{k}{\ell}=-\frac{\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$
y cuando $h,\ell\rightarrow 0$ se tiene
$$\frac{dz}{dy}=-\frac{\frac{\partial F}{\partial y}(x_{0},y_{0},z_{0})}{\frac{\partial F}{\partial z}(x_{0},y_{0},z_{0})}$$ $\square$