MATERIAL EN REVISIÓN

Introducción

En la entrada anterior probamos que la clase de conjuntos medibles es cerrada bajo uniones e intersecciones numerables. En esta sección usaremos dichos resultados para ver que la clase de conjuntos medibles contiene a prácticamente todos los conjuntos interesantes al menos desde un punto de vista topológico (por ejemplo abiertos, cerrados, compactos, junto con uniones e intersecciones numerables de estos). También veremos como podemos usar estos conjuntos para aproximar conjuntos medibles más generales y como es que esto caracteriza completamente a los conjuntos medibles.

Lema. Cualquier conjunto abierto $U$ se puede expresar como una unión numerable de rectángulos abiertos.

Demostración. Para cualquier $x\in U$, podemos encontrar un rectángulo abierto $Q$, tal que $x\in Q\subseteq U$. Más aún, podemos elegir $Q$ de tal manera que sus intervalos componente tengan extremos racionales (basta «encoger» un poco dichos intervalos). Si denotamos por ${\mathcal{R}}_{\mathbb{Q}}$ al conjunto de rectángulos abiertos con extremos racionales, tenemos que: $$U=\bigcup _{Q\in {\mathcal{R}}_{\mathbb{Q}};Q\subseteq U}Q.$$ La contención $\supseteq$ es obvia. La contención $\subseteq$ se sigue del hecho de que cada $p\in U$ está contenido en algún tal rectángulo. Como ${\mathcal{R}}_{\mathbb{Q}}$ es de hecho un conjunto numerable (¿Porqué?), resulta que la unión anterior es numerable. Se sigue el Lema.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Corolario. Los conjuntos abiertos, cerrados, compactos y las uniones e intersecciones numerables de estos son medibles.
Demostración. Del Lema y nuestros teoremas de cerradura, se sigue de inmediato que los abiertos son conjuntos medibles. Los cerrados (incluyendo los compactos) son medibles al ser complementos de abiertos. Las uniones e intersecciones numerables de estos son medibles, de nuevo, por nuestros teoremas de cerradura.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Los resultados anteriores nos dan una manera rápida de verificar si un conjunto es medible, aunque no nos dicen nada sobre el valor de la medida de Lebesgue. En general, suele ser complicado calcular la medida de Lebesgue de un conjunto sin usar herramientas de teoría de integración (que veremos más adelante). Veamos un ejemplo de como hacerlo directamente.

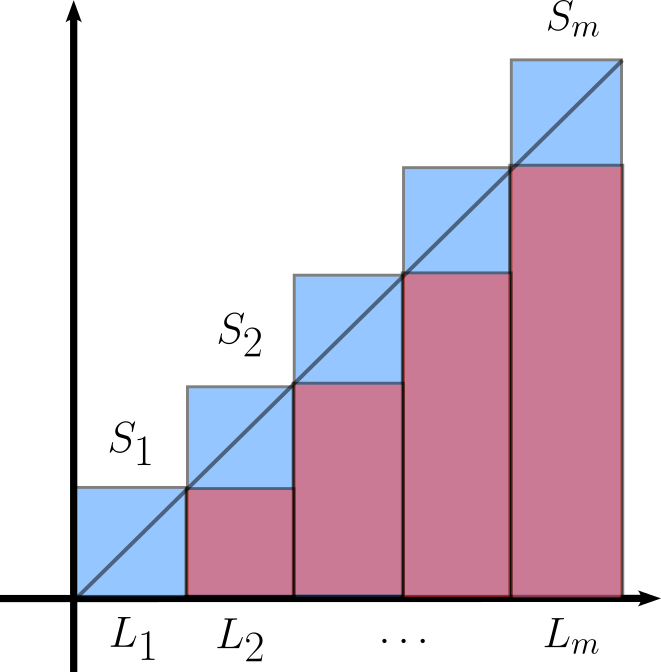
Ejercicio. Calcula la medida de Lebesgue del triángulo $$T=\{(x,y)\in {\mathbb{R}}^2:0\le x\le 1,0\le y\le x\}.$$

Solución. Claramente $T$ es cerrado así que es un conjunto medible. Fijemos $m\in \mathbb{N}$. Definamos los rectángulos: $$L_k=[\frac{k-1}{m},\frac{k}{m}]\times [0,\frac{k-1}{m}]$$ $$S_k=[\frac{k-1}{m},\frac{k}{m}]\times [0,\frac{k}{m}]$$ Para $k=1,2,\dots ,m$. Observemos que $$\bigcup _{k=1}^m{L}_k\subseteq T\subseteq \bigcup _{k=1}^m{S}_k.$$ Además los $L_k$ y los $S_k$ son ajenos salvo en conjuntos de medida cero, Luego: $$\lambda \left(\bigcup _{k=1}^m{L}_k\right)\le \lambda (T)\le \lambda \left(\bigcup _{k=1}^m{S}_k\right)$$ $$⟹\sum _{k=1}^m\lambda (L_k)\le \lambda (T)\le \sum _{k=1}^m\lambda (S_k)$$ $$⟹\sum _{k=1}^m\left(\frac{1}{m}\right)\left(\frac{k-1}{m}\right)\le \lambda (T)\le \sum _{k=1}^m\left(\frac{1}{m}\right)\left(\frac{k}{m}\right)$$ $$⟹\frac{1}{m^2}\sum _{k=1}^m(k-1)\le \lambda (T)\le \frac{1}{m^2}\sum _{k=1}^{m}k$$ $$⟹\frac{1}{m^2}\left(\frac{(m-1)(m)}{2}\right)\le \lambda (T)\le \frac{1}{m^2}\left(\frac{(m)(m+1)}{2}\right)$$ $$⟹\frac{1}{2}\frac{m-1}{m}\le \lambda (T)\le \frac{1}{2}\frac{m+1}{m}.$$ Haciendo $m⟶\mathrm{\infty }$ concluimos que $\lambda (T)=\frac{1}{2}$.

$\mathrm{△}$

Observación. El ejercicio anterior te debería de recordar un poco a las sumas de Riemann, la notación $L_k$ y $S_k$ es sugerente. Esto no es casualidad. El método anterior nos puede servir en general para probar que la medida de la región debajo de la gráfica de una función Riemann-integrable (no negativa) $G$ es igual a la intregal de Riemann. Las expresiones de las sumas inferiores y superiores nos dicen exactamente como construir colecciones de rectángulos (ajenos salvo en conjuntos de medida cero) que aproximen la región «por abajo» y «por arriba». Por monotonía dichas sumas solo se pueden acercar a $\lambda (G)$, que por definición, debe ser la integral de Riemann. Más adelante analizaremos con todo detalle esta clase de problemas.

Aproximación de conjuntos medibles

La siguiente proposición es relevante pues nos dice que podemos «aproximar» un conjunto medible con conjuntos abiertos o compactos. Estos conjuntos tienen propiedades topológicas y de convergencia muy interesantes, lo que a menudo sirve para establecer teoremas de existencia o probar estimados más fuertes.

Teorema (de aproximación de conjuntos medibles.) Si $A$ es un conjunto medible, entonces $$\lambda (A)=\underset{A\subseteq U\text{ abierto}}{inf}\{\lambda (U)\}=\underset{K\subseteq A\text{ compacto}}{sup}\{\lambda (U)\}.$$
Demostración. La primera igualdad ya la establecimos en general para la medida exterior.
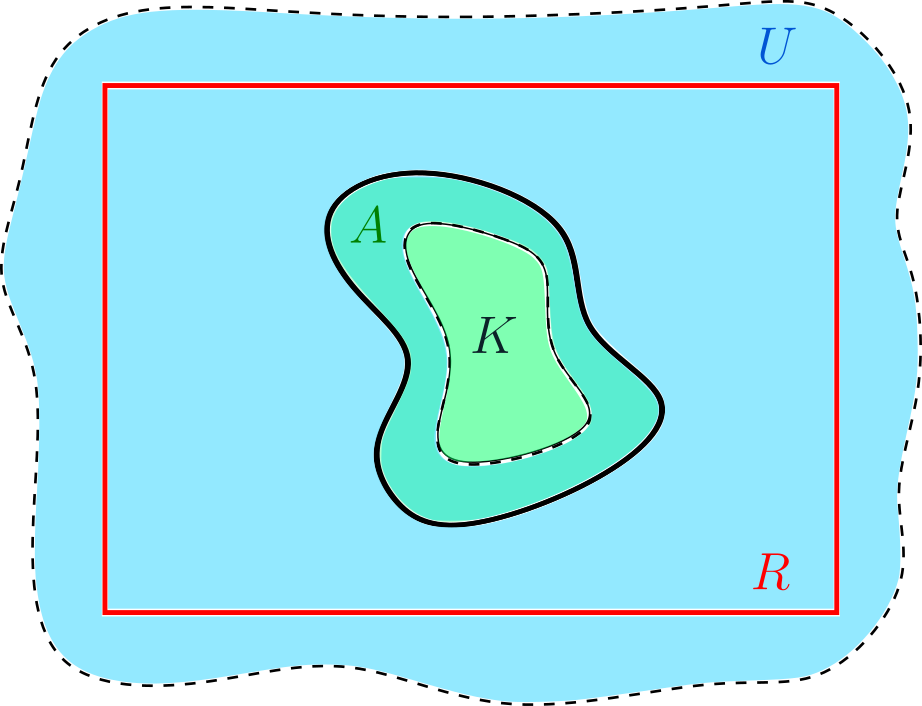
Veamos la segunda igualdad: $\lambda (A)=\underset{K\subseteq A\text{ compacto}}{inf}\{\lambda (U)\}$. Consideremos primero el caso en el que $A$ es acotado. Tomemos $R$ un rectángulo cerrado suficientemente grande tal que $A$ esté contenido en el interior de $R$. Los conjuntos $A$ y $R\setminus A$ son medibles con medida finita.

Por la primera igualdad, dado $\epsilon >0$ podemos tomar un abierto $U$ tal que $R\setminus A\subseteq U$ y $$\lambda (U)<\lambda (R\setminus A)+\epsilon .$$ Notemos que $K=R\cap U^c$ es un conjunto compacto (cerrado y acotado) con $K\subseteq A$ (observa la figura), además $A\setminus K\subseteq U\setminus (R\setminus A)$. Luego, por la aditividad: $$\lambda (A)-\lambda (K)=\lambda (A\setminus K)\le \lambda (U\setminus (R\setminus A))=\lambda (U)-\lambda (R\setminus A)<\epsilon$$ $$⟹\lambda (K)\le \lambda (A)<\lambda (K)+\epsilon .$$ Como podemos hacer esto para cualquier $\epsilon >0$ concluimos que cuando $A$ es acotado se da la igualdad.

Si $A$ es de medida finita pero no necesariamente acotado, dado $\epsilon >0$, podemos tomar la sucesión: $B_k=A\cap R_k$ donde $R_k=[-k,k{]}^n$. Claramente $B_1\subseteq B_2\subseteq \dots$ y $A=\bigcup _{k=1}^{\mathrm{\infty }}{B}_k$. Por la monotonía de la medida de Lebesgue tenemos que $\lambda (B_k)\uparrow \lambda (A)$ cuando $k\to \mathrm{\infty }$, de modo que podemos encontrar algún $N$ suficientemente grande tal que $$\lambda (B_N)\le \lambda (A)<\lambda (B_N)+\frac{\epsilon }{2}.$$ Como $B_N$ es acotado, por el caso anterior, podemos encontrar algún compacto $K\subseteq B_N\subseteq A$ tal que $$\lambda (K)\le \lambda (B_N)<\lambda (K)+\frac{\epsilon }{2}.$$ Luego: $$\lambda (A)<\lambda (B_N)+\frac{\epsilon }{2}<\lambda (K)+\frac{\epsilon }{2}+\frac{\epsilon }{2}=\lambda (K)+\epsilon .$$ Como podemos hacer esto para cualquier $\epsilon >0$ concluimos que $\lambda (A)=\underset{K\subseteq A\text{ compacto}}{sup}\{\lambda (U)\}$ cuando $A$ es de medida finita.
El caso en el que $A$ es de medida infinita se queda como tarea moral.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Caracterización de conjuntos medibles

La proposición anterior es de interés pues de hecho caracteriza completamente a los conjuntos medibles con medida finita.

Lema (Completitud de la medida de Lebesgue.) Si $A\subseteq B\subseteq C$ son subconjuntos de ${\mathbb{R}}^n$, $A$ y $C$ son medibles con $\lambda (A)=\lambda (C)<\mathrm{\infty }$, entonces $B$ es medible y $\lambda (A)=\lambda (B)=\lambda (C)$.

Demostración. Nota que $C\setminus A$ es un conjunto medible con $$\lambda (C\setminus A)=\lambda (C)-\lambda (A)=0.$$ Como $B\setminus A\subseteq C\setminus A$, entonces $${\lambda }^{\ast }(B\setminus A)\le {\lambda }^{\ast }(C\setminus A)=\lambda (C\setminus A)=0.$$ $⟹B\setminus A$ es medible al ser un conjunto nulo. Como $B=A\cup (B\setminus A)$, se sigue que $B$ es medible. Por monotonía necesariamente $\lambda (A)=\lambda (B)=\lambda (C)$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Teorema (Caracterización de conjuntos medibles). Sea $A\subseteq {\mathbb{R}}^n$ un subconjunto con ${\lambda }^{\ast }(A)<\mathrm{\infty }$. Entonces $A$ es medible si y sólo si $${\lambda }^{\ast }(A)=\underset{A\subseteq U\text{ abierto}}{inf}\{\lambda (U)\}=\underset{K\subseteq A\text{ compacto}}{sup}\{\lambda (U)\}.$$

Demostración. La implicación ($⟹$) es precisamente el teorema de aproximación. Veamos la implicación ($⟸$).

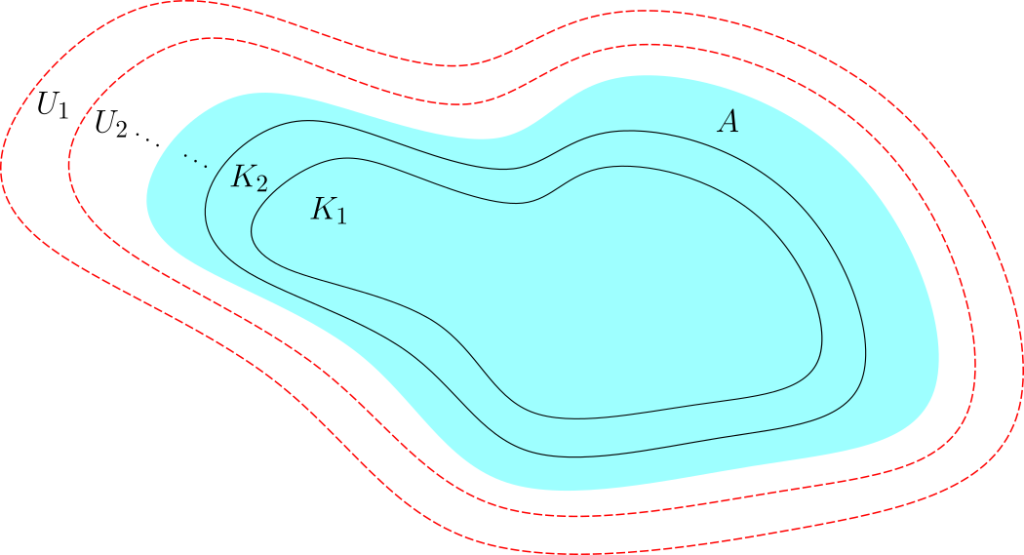
Supongamos que $\underset{A\subseteq U\text{ abierto}}{inf}\{\lambda (U)\}=\underset{K\subseteq A\text{ compacto}}{sup}\{\lambda (U)\}$, entonces, por definición de ínfimo, para cada $m=1,2,\dots$ podemos encontrar un abierto $U_m$ y un compacto $K_m$ tales que $K_m\subseteq A\subseteq U_m$ y $$\lambda (U_m)<{\lambda }^{\ast }(A)+\frac{1}{2m};$$ $${\lambda }^{\ast }(A)<\lambda (K_m)+\frac{1}{2m}.$$ Es decir $$\lambda (U_m\setminus K_m)=\lambda (U_m)-\lambda (K_m)<{\lambda }^{\ast }(A)+\frac{1}{2m}-{\lambda }^{\ast }(A)+\frac{1}{2m}=\frac{1}{m}.$$ Tomando $U_m^{\prime }=\bigcap _{j=1}^m{U}_j$ y $K_m^{\prime }=\bigcup _{j=1}^m{K}_j$, es inmediato que $K_m^{\prime }\subseteq A\subseteq U_m^{\prime }$ y $\lambda (U_m^{\prime }\setminus K_m^{\prime })\le \lambda (U_m\setminus K_m)<\frac{1}{m}$, así que podemos suponer sin pérdida de generalidad que $U_1\supseteq U_2\supseteq \dots$ y $K_1\subseteq K_2\subseteq \dots$.

Definamos $F=\bigcap _{j=1}^{\mathrm{\infty }}{U}_j$ y $G=\bigcup _{j=1}^{\mathrm{\infty }}{K}_j$. Estos son medibles al ser uniones e intersecciones numerables de conjuntos medibles respectivamente. Claramente $G\subseteq A\subseteq F$, además $$F\setminus G=(\bigcap _{j=1}^{\mathrm{\infty }}{U}_j)\cap (\bigcup _{j=1}^{\mathrm{\infty }}{K}_j{)}^c=(\bigcap _{j=1}^{\mathrm{\infty }}{U}_j)\cap (\bigcap _{j=1}^{\mathrm{\infty }}{K}_j^c)=\bigcap _{j=1}^{\mathrm{\infty }}(U_j\cap K_j^c)$$ $$=\bigcap _{j=1}^{\mathrm{\infty }}(U_j\setminus K_j).$$ Notemos que $U_1\setminus K_1\supseteq U_2\setminus K_2\supseteq \dots$ y $U_1\setminus K_1$ es de medida finita. Se sigue por monotonía de la medida de Lebesgue: $$\lambda (U_j\setminus K_j)\downarrow \lambda (F\setminus G).$$ Pero como $0\le \lambda (U_j\setminus K_j)<\frac{1}{j}$ para $j=1,2,\dots$ la única posibilidad es que $\lambda (U_j\setminus K_j)\to 0$ cuando $j\to \mathrm{\infty }$. Luego $$\lambda (F\setminus G)=0.$$ $$⟹\lambda (F)=\lambda (G)+\lambda (F\setminus G)=\lambda (G).$$
Como $G\subseteq A\subseteq F$; $G$ y $F$ son medibles con medida finita y $\lambda (F)=\lambda (G)$, se sigue por el Lema anterior que $A$ es medible.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Siguiendo la línea de la proposición anterior, veamos un par de equivalencias más para conjuntos medibles.

Teorema (Equivalencia de conjuntos medibles). Las siguientes son equivalentes.

1. $A$ es un conjunto medible.
2. Para cualquier $\epsilon >0$ existe un abierto $U$ tal que $A\subseteq U$ y ${\lambda }^{\ast }(U\setminus A)<\epsilon$.
3. Para cualquier $\epsilon >0$ existe un cerrado $K$ tal que $K\subseteq A$ y ${\lambda }^{\ast }(A\setminus K)<\epsilon$

Demostración. Probaremos la equivalencia ($1⟺2$). La tercera se queda como tarea moral.

Si $A$ es de medida finita, la implicación (1$⟹$2) es consecuencia inmediata del teorema anterior.

Si $A$ es de medida infinita, podemos partirlo en una cantidad numerable de conjuntos medibles ajenos con medida finita: $A=\bigcup _{k=1}^{\mathrm{\infty }}{B}_k$ (piensa por ejemplo en intersecar $A$ con cada rectángulo semiabierto de la forma $[p_1,p_1+1)\times [p_2,p_2+1)\times \cdots \times [p_n,p_n+1)$ donde $p_1,p_2,\dots p_n$ son todos enteros).

Para cada $B_k$, podemos encontrar un abierto $U_k$ tal que $B_k\subseteq U_k$ y $\lambda (U_k\setminus B_k)<\frac{\epsilon }{2^k}$. Sea $U=\bigcup _{k=1}^{\mathrm{\infty }}{U}_k$. Éste es abierto con $A\subseteq U$, además tenemos $U\setminus A\subseteq \bigcup _{k=1}^{\mathrm{\infty }}(U_k\setminus B_k)$. Por monotonía y subaditividad: $$\lambda (U\setminus A)\le \sum _{k=1}^{\mathrm{\infty }}\lambda (U_k\setminus B_k)<\sum _{k=1}^{\mathrm{\infty }}\frac{\epsilon }{2^k}=\epsilon .$$
Con esto concluimos que (1$⟹$2).
Ahora supongamos 2. En particular para cada $k=1,2,\dots$ podemos encontrar un abierto $U_k$ tal que $A\subseteq U_k$ y ${\lambda }^{\ast }(U_k\setminus A)<\frac{1}{k}$. Más aún, imitando el argumento de la equivalencia anterior, podemos suponer sin pérdida de generalidad que $U_1\supseteq U_2\supseteq \dots$. Consideremos $G=\bigcap _{k=1}^{\mathrm{\infty }}{U}_k$. Éste es medible con $A\subseteq G$, además $G\setminus A\subseteq U_k\setminus A$ para todo $k=1,2,\dots$ por lo que $${\lambda }^{\ast }(G\setminus A)\le {\lambda }^{\ast }(U_k\setminus A)<\frac{1}{k}\mathrm{\forall }k=1,2,\dots$$ De donde $${\lambda }^{\ast }(G\setminus A)=0.$$ Así que $G$ y $G\setminus A$ son medibles (éste último al ser nulo). Se sigue que $A=G\setminus (G\setminus A)$ es medible como queríamos probar.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Más adelante…

Estudiaremos la estructura «conjuntista» de los conjuntos medibles. Esto será de utilidad, por un lado para definir rápidamente el concepto de función medible; pero también para construir nociones de integración sobre espacios abstractos como veremos al final del curso.

Tarea moral

• Completa la demostración del teorema de aproximación de conjuntos medibles. [
  Sugerencia: Imita el argumento en el caso en el que $A$ es de medida finita, encontrando compactos con medida arbitrariamente grande contenidos en $A$].
• Demuestra la equivalencia del punto 3. en el Teorema de equivalencia de conjuntos medibles. [Sugerencia: Puedes usar la equivalencia ($1⟺2$) con el complemento de $A$].