Introducción

En la entrada anterior, definimos los espacios $L^p$ y analizamos algunas de sus propiedades fundamentales. Entre otros resultados, demostramos que son espacios normados y establecimos desigualdades clave relacionadas con ellos.

En esta ocasión, probaremos una propiedad analítica de gran importancia: los espacios $L^p$ son espacios de Banach.

Para esta entrada, $(X,\mathcal{M},\mu)$ denota un espacio de medida arbitrario salvo que se especifique lo contrario.

A modo de recordatorio:

Definición. Decimos que un espacio vectorial normado $(V,\left\lVert \cdot \right\lVert)$ es un espacio de Banach si es completo respecto a la métrica inducida por la norma: $d(u,v)=\left\lVert u-v \right\lVert$.

Antes de continuar, veamos un Lema que simplificará los desarrollos más adelante:

Lema. Sea $1\leq p < \infty$.Supongamos que $\{ f_k\}_{k=1}^{\infty}\subseteq L^p$ y $f_k\geq 0$ $\forall k$. Entonces: $$\left\lVert \sum_{k=1}^{\infty} f_k \right\lVert_p\leq \sum_{k=1}^{\infty} \left\lVert f_k \right\lVert_p.$$

Demostración. Sea $$F_N=\sum_{k=1}^{N} f_k.$$

Por la desigualdad de Minkowski: $$\left\lVert F_N \right\lVert_p\leq \sum_{k=1}^{N} \left\lVert f_k \right\lVert_p\leq \sum_{k=1}^{\infty} \left\lVert f_k \right\lVert_p.$$

Entonces, por el teorema de la convergencia monótona y la continuidad de la función $x\to x^p$, se sigue:

\begin{align*}
\left\lVert \sum_{k=1}^{\infty}f_k \right\lVert_p &= \left(\int_X \left|\sum_{k=1}^{\infty}f_k\right|^p \ \mathrm{d}\mu \right)^{\frac{1}{p}} \\
&= \left(\int_X \left|\lim_{N\to \infty} F_N\right|^p \ \mathrm{d}\mu \right)^{\frac{1}{p}} \\
&= \lim_{N\to \infty}\left(\int_X \left| F_N\right|^p \ \mathrm{d}\mu \right)^{\frac{1}{p}} \\
&= \lim_{N\to \infty} \left\lVert F_N \right\lVert_p \\
&\leq \sum_{k=1}^{\infty} \left\lVert f_k \right\lVert_p.
\end{align*}

$\square$

Teorema (Riesz-Fischer). Sea $(X,\mathcal{M},\mu)$ un espacio de medida y sea $1\leq p <\infty$. Entonces, el espacio normado $(L^p(X),\left\lVert f \right\lVert_p)$ es un espacio de Banach.

Demostración. Consideremos una sucesión de Cauchy $\{ f_k\}_{k=1}^{\infty} $ en $L^p$. Al ser de Cauchy, podemos encontrar recursivamente una subsucesión $\{ f_{k_r} \}_{r=1}^{\infty}$ tal que: \begin{equation}\left\lVert f_{k_{r+1}}-f_{k_r} \right\lVert_p<\frac{1}{2^r} \ \ \ \forall r\in \mathbb{N}.\end{equation}

Basta probar que la subsucesión $\{ f_{k_r} \}_{r=1}^{\infty}$ converge en $L^p$. Recordemos que si una subsucesión de una sucesión de Cauchy converge, entonces toda la sucesión converge al mismo límite. Por simplicidad, reenumeremos los índices y supongamos que $\{ f_{k_r} \}_{r=1}^{\infty}=\{ f_{k} \}_{k=1}^{\infty}$.

Definamos $$F=|f_1|+\sum_{j=1}^{\infty} |f_{j+1}-f_j|.$$ Ésta es una función $\mathcal{M}$-medible al ser una serie de funciones medibles. Por el Lema anterior y (1) tenemos que:

\begin{align*}
\left\lVert F \right\lVert_p &\leq \left\lVert f_1 \right\lVert_p+\left\lVert \sum_{k=1}^{\infty} |f_{j+1}-f_j| \right\lVert_p \\
&\leq \left\lVert f_1 \right\lVert_p+\sum_{k=1}^{\infty}\left\lVert f_{j+1}-f_j \right\lVert_p \\
&\leq \left\lVert f_1 \right\lVert_p+\sum_{j=1}^{\infty} \frac{1}{2^j} \\
&= \left\lVert f_1 \right\lVert_p+1 \\ &<\infty.
\end{align*}

En particular, se sigue que $F^p$ es integrable, de modo que $F^p<\infty$ en c.t.p., o equivalentemente, que $F(x)<\infty$ para todo $x\in X\setminus N$ con $N$ algún conjunto nulo: $\mu(N)=0$.

Para cualquier $x\in X\setminus N$, $F(x)=|f_1(x)|+\sum_{j=1}^{\infty} |f_{j+1}(x)-f_j(x)|$ converge $\implies$ $f_1(x)+\sum_{j=1}^{\infty} (f_{j+1}(x)-f_j(x))$ converge absolutamente. Como la $k$-ésima suma parcial de la serie «telescópica» anterior es: $$f_1(x)+\sum_{j=1}^{k} (f_{j+1}(x)-f_j(x))=f_k(x).$$ Se sigue que $$f(x)=\lim_{k\to \infty} f_k(x).$$ Existe para cada $x\in X\setminus N$. Definiendo $f=0$ sobre $N$, es fácil ver que $f$ resulta ser $\mathcal{M}$-medible.

Como para cada $x\in X\setminus N$ $$f(x)=f_1(x)+\sum_{j=1}^{\infty}(f_{j+1}(x)-f_j(x)) $$ \begin{equation}\implies |f(x)-f_k(x)|=\left|\sum_{j=k+1}^{\infty}(f_{j+1}(x)-f_j(x))\right|\leq \sum_{j=k+1}^{\infty}|f_{j+1}(x)-f_j(x)|. \end{equation} Observa que este último estimado nos dice que para $x\in X\setminus N$, $$ |f(x)-f_k(x)|\leq \sum_{j=k+1}^{\infty}|f_{j+1}(x)-f_j(x)| \longrightarrow 0 $$ Cuando $k\to \infty$, pues $\sum_{j=1}^{\infty}(f_{j+1}(x)-f_j(x))$ es una serie convergente. Es decir, $f_k(x)\longrightarrow f(x)$ para $x\in X\setminus N$. Debajo enunciamos este hecho como un corolario.

Se sigue del Lema, (1) y (2) que: \begin{align*}
\left\lVert f-f_k \right\lVert_p &\leq \left\lVert \sum_{j=k+1}^{\infty}|f_{j+1}-f_j| \right\lVert_p \\
&\leq \sum_{j=k+1}^{\infty} \left\lVert f_{j+1}-f_j \right\lVert_p \\
&\leq \sum_{j=k+1}^{\infty} \frac{1}{2^{j}} \\
&= \frac{1}{2^{k}}<\infty.
\end{align*} Por lo anterior, tenemos por un lado que $$\left\lVert f-f_k \right\lVert_p<\infty.$$ $\implies$ $(f-f_k)\in L^p$. Luego $f=(f-f_k)+f_k\in L^p$. Se sigue también que $$\lim_{k\to \infty} \left\lVert f-f_k \right\lVert_p=0.$$ Por lo que $f_k \longrightarrow f$ en $L^p$.

$\square$

Corolario. Si una sucesión $f_k\longrightarrow f$ en $L^p$, entonces existe una subsucesión ${ f_{k_r}}$ tal que $$\lim_{r\to \infty} f_{k_r}(x)=f(x)$$ En c.t.p. $x\in X$.

Modos de convergencia

El corolario anterior podría sugerir alguna relación entre la convergencia en $L^p$ y la convergencia en casi todo punto. Sin embargo, esta cuestión es complicada. Dedicaremos esta sección a estudiar la relación que existe entre los distintos modos de convergencia que hemos construido.

Repasemos las múltiples nociones de convergencia de funciones que conocemos hasta ahora:

1. Convergencia puntual. $f_k\longrightarrow f$ puntualmente si $f_k(x)\longrightarrow f(x)$ para todo $x\in X$.
2. Convergencia uniforme. $f_k \longrightarrow f$ uniformemente si $\forall \varepsilon>0$, existe $\delta>0$ tal que $|f(x)-f_k(x)|<\varepsilon$ para todo $x\in X$.
3. Convergencia en casi todo punto. $f_k\longrightarrow f$ en casi todo punto si existe un conjunto nulo $N$ tal que $f_k(x)\longrightarrow f(x)$ para todo $x\in X\setminus N$.
4. Convergencia en $L^p$. $f_k\longrightarrow f$ en $L^p$ si $ \left\lVert f-f_k \right\lVert_p\longrightarrow 0$.

Es claro que 2. $\implies$ 1. $\implies$ 3. Es fácil construir ejemplos en los que 1.$\;\not\!\!\!\implies$ 2. ni 3.$\;\not\!\!\!\implies$1. Veamos algunos casos en los que 1. $\;\not\!\!\!\implies$4. ni 4.$\;\not\!\!\!\implies$ 3.

Ejemplo. Consideremos $(\mathbb{R}, \mathcal{L},\lambda)$ los reales con la medida de Lebesgue. Definamos: $$f_k=\frac{1}{k}\chi_{[0,k^p]}.$$

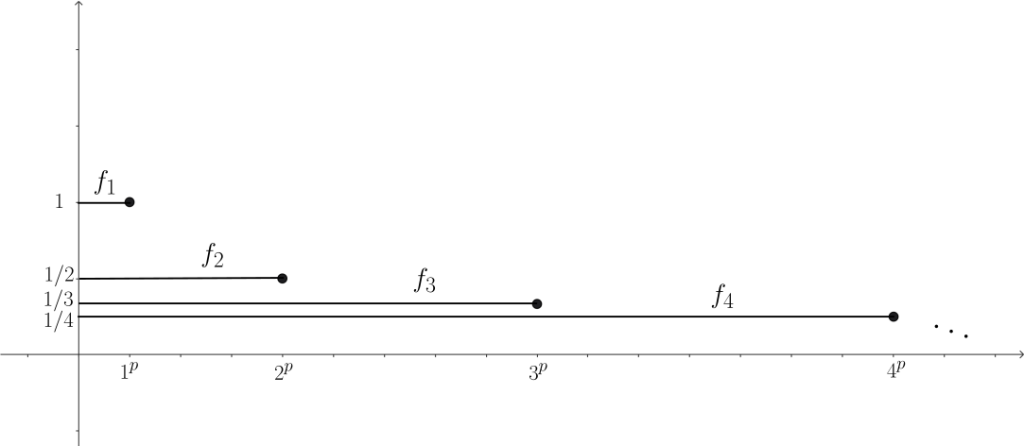
Afirmamos que esta sucesión de funciones converge uniformemente a 0 (en particular puntualmente y en c.t.p.), pero no converge en $L^p$.

• La convergencia uniforme es clara: Si $k\geq \frac{1}{\varepsilon}$, entonces $\forall x\in \mathbb{R}$ $|f_k(x)-0|=|f_k(x)|\leq \frac{1}{k}\leq \varepsilon$.
• Si $f_k$ converge en $L^p$, digamos a $f$, por el corolario existiría alguna subsucesión $\{f_{k_r}\}_{r=1}^{\infty}$ que converge en c.t.p. a $f$. Como $f$ converge uniformemente a 0, la única posibilidad es $f=0$. Veamos que $f_k$ NO converge a 0 en $L^p$: Para todo $k\in \mathbb{N}$ \begin{align*}
  \left\lVert f_k-0 \right\lVert_p &= \left( \int_{\mathbb{R}}|\frac{1}{k}\chi_{[0,k^p]}(x)|^p \ \mathrm{d}x\right)^{\frac{1}{p}} \\
  &= \frac{1}{k}\left( \int_0^{k^p}1 \ \mathrm{d}x\right)^{\frac{1}{p}} \\
  &= \frac{1}{k}\left( k^p \right)^{\frac{1}{p}} \\
  &= 1 \neq 0.
  \end{align*} Por lo que $f_k$ NO converge a 0 en $L^p$.

$\triangle$

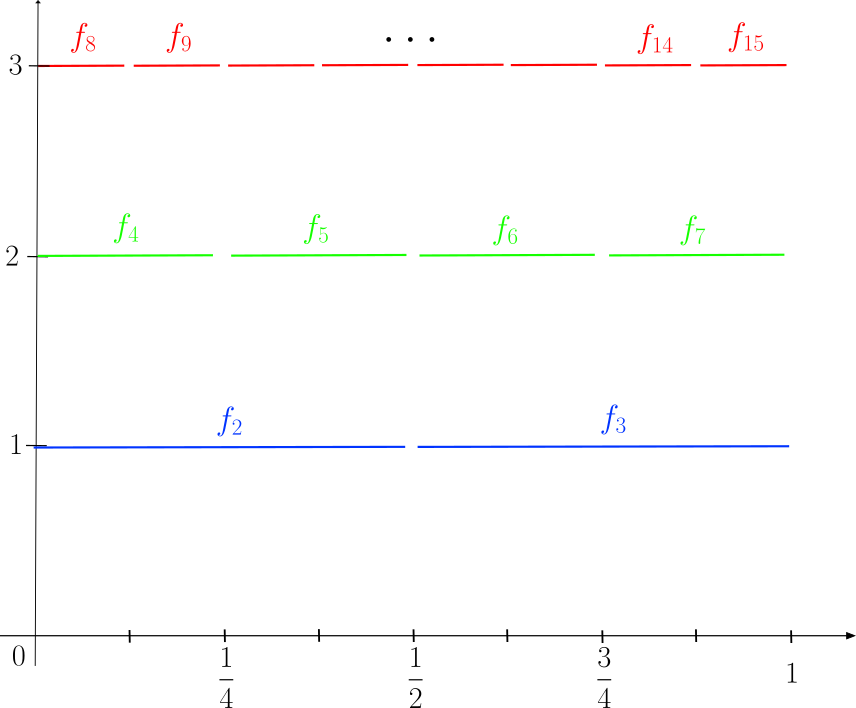
Ejemplo. Consideremos ahora la medida de Lebesgue restringida en el intervalo $[0,1]$, $\lambda_{|[0,1]}$. Para cada $k\in \mathbb{N}$ definamos: $$f_{2^k+j}=k\chi_{\left[\frac{j}{2^k},\frac{j+1}{2^k}\right]}; \ \ \ \ \ j=0,1,\dots, 2^{k}-1.$$

Afirmamos que $f_k\longrightarrow 0$ en $L^p$ para cada $p\in[1,\infty)$, pero $f_k$ NO converge en c.t.p.

• Dado $p\in [1,\infty)$: \begin{align*} \left\lVert f_{2^k+j} \right\lVert_p &= \left( \int_0^1 k^p\chi_{\left[\frac{j}{2^k},\frac{j+1}{2^k}\right]} \ \mathrm{d}\lambda \right)^{\frac{1}{p}} \\
  &= k \left( \int_{\frac{j}{2^j}}^{\frac{j+1}{2^k}} 1 \ \mathrm{d}x \right)^{\frac{1}{p}} \\
  &= k\left( \frac{1}{2^k} \right)^{\frac{1}{p}} \\
  &= k\cdot 2^{-\frac{k}{p}} \longrightarrow 0.
  \end{align*} Cuando $2^k+j\longrightarrow \infty$, de modo que $f_k \longrightarrow 0 $ en $L^p$ para $p\in [1,\infty)$.
• Sin embargo, la sucesión $\{ f_m(x)\}_{m=1}^{\infty}$ no converge para ningún $x\in[0,1]$:
  Dado $N>0$, podemos encontrar $m=2^k+j>N$ tal que $x\in [\frac{j}{2^k},\frac{j+1}{2^k}]$ $\implies$ $f_{2^k+j}(x)=k$. Sin embargo, también podemos encontrar algún $m’=2^k+i$ tal que $x\notin [\frac{i}{2^k},\frac{i+1}{2^k}]$ $\implies$ $f_{2^k+j}(x)=0$. Concluimos que $$\limsup_{j\to \infty} f_j(x)=\infty \neq 0 = \liminf_{j\to \infty} f_j(x).$$ Así que la sucesión NO converge en ningún punto.

$\triangle$

Ejemplo. Una sucesión en $L^{p_1}\cap L^{p_2}$ puede converger en $L^{p_1}$ pero no en $L^{p_2}$. Consideremos nuevamente $(\mathbb{R},\mathcal{L},\lambda)$ y definamos: $$f_k=k^{-1}\chi_{(k,2k)}.$$ De manera que $$\left\lVert f_k \right\lVert_p=\left( \int_{\mathbb{R}} (k^{-1}\chi_{(k,2k)})^p\right)^{\frac{1}{p}}=k^{-1}(k)^{\frac{1}{p}}=k^{-1+\frac{1}{p}}.$$ Por tanto $f_k \in L^p$ para todo $k\in \mathbb{N}$ y para todo $p\in [1,\infty)$. Sin embargo

• $f_k \longrightarrow 0$ en $L^p$ si $1<p<\infty$, pues $\left\lVert f_k \right\lVert_p=k^{-1+\frac{1}{p}}\longrightarrow 0$.
• $\left\lVert f_k \right\lVert_1=1$ $ \ \forall k$, por lo que $f_k$ no converge a 0 en $L^1$.

$\triangle$

Más adelante…

Introduciremos el espacio $L^\infty$. Un espacio importante que se puede pensar como «un caso límite de los espacios $L^p$», y que comparte varias de sus propiedades analíticas.

Tarea moral…

• Sea $f_k(x)=\min(x^{-\frac{1}{2}},k)$ $\forall x\in [0,1]$. Verifica que $\{ f_k\}_{k=1}^{\infty}$ es una sucesión de Cauchy en $L^p([0,1])$ ($1\leq p \leq \infty$). Encuentra el límite de la sucesión en $L^p$.
• Sea $f_k(x)=\min(1,kx)$ $\forall x \in [0,1]$. Verifica que $f_k$ es una sucesión de Cauchy en $L^p([0,1])$ y encuentra su límite.
• (no-compacidad de la bola unitaria). Sea $f_k=\chi_{[k,k+1]}$ para cada $k\in \mathbb{N}$.
  • Calcula $\left\lVert f_k \right\lVert_p$ para cada $k$.
  • ¿Es $f_k$ una sucesión de Cauchy en $L^p(\mathbb{R})$?
  • ¿Tiene alguna subsucesión convergente?
  • Deduce que la bola unitaria en $L^p(\mathbb{R})$: $B=\{ f\in L^p(\mathbb{R}) \ | \ \left\lVert f \right\lVert_p=1\}$ no es un conjunto compacto.
• Demuestra que las funciones simples, es decir de la forma $s=\sum_{k=1}^{m}\alpha_k\chi_{A_k}$ con $\alpha_k\in \mathbb{R}$ y $A_k\in \mathcal{M}$ para $k=1,\dots, m$ son densas en $L^p(X,\mathcal{M},\mu)$. Esto es, que para cualquier $f\in L^p$ y $\varepsilon>0$, existe una función simple $s$ tal que $\left\lVert f-s \right\lVert_p<\varepsilon$. [SUGERENCIA: Ya probamos que podemos aproximar puntualmente a $f$ por funciones simples $s_k$ tales que $|s_k|\leq f$].
• (convergencia uniforme y en $L^p$).
  • Demuestra que la convergencia uniforme en $[0,1]$ implica la convergencia en $L^p([0,1])$.
  • Sea $\{f_i\}_{i\in I}$ un conjunto de funciones diferenciables en $[0,1]$ tales que existe $0<M<\infty$ con $|f_i|,|f’_i|<M$ $\forall i \in I$. Demuestra que $\{f_i\}_{i\in I}$ es un conjunto compacto en $L^p([0,1])$. [SUGERENCIA: Utiliza el inciso anterior y el teorema de Arzela-Ascoli. El teorema del valor medio es útil para verificar la hipótesis de equicontinuidad].