Introducción

En esta sección se definen los distintos planos que podemos caracterizar a partir de vectores especiales en el espacio $\mathbb{R}^n$

Plano Tangente

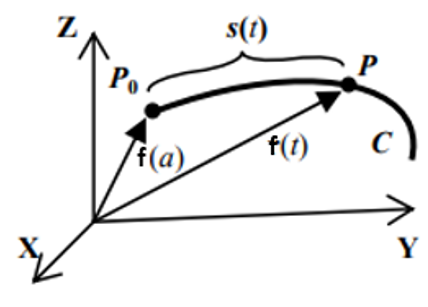
Sea $f:[a,b]\rightarrow\mathbb{R}^{n}$ una curva tal que el vector derivada $f'(t)\neq 0$ para todo $t\in[a,b]$, es tangente a f y apunta en la dirección que el parámetro t crece.
Definición. Dada una curva $f:[a,b]\rightarrow\mathbb{R}^{n}$, el vector unitario tangente $T$ es otra función vectorial asociada a la curva, y está definida por:
\[
T(t)=\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\ \ \ \ \text{si}\ \ \ \|f^{\prime}(t)\| \neq 0.
\]
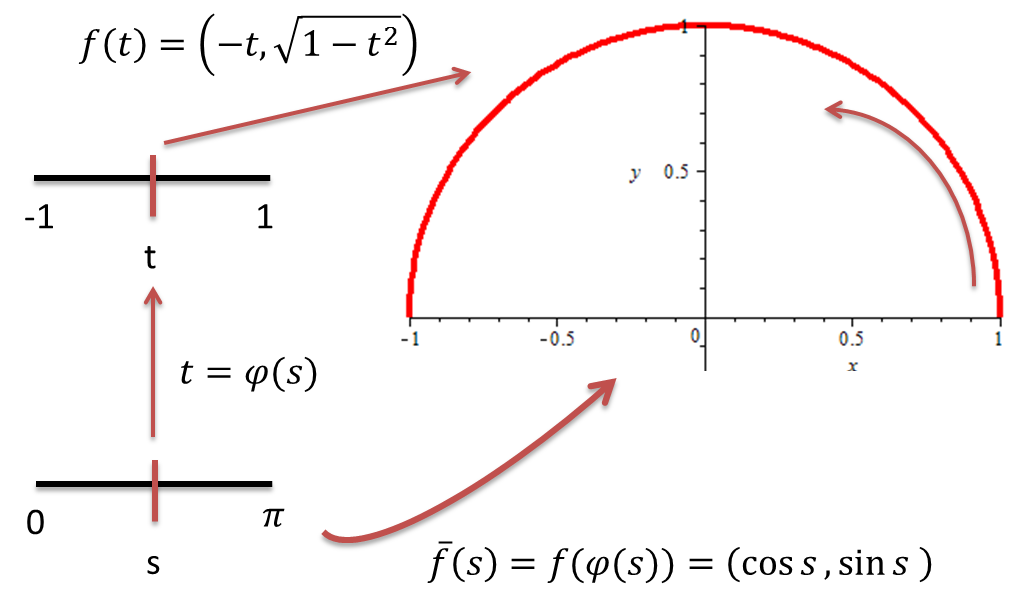
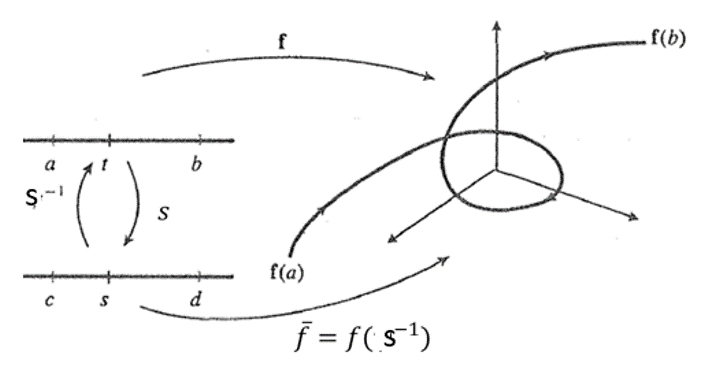
Si en la definición anterior, la curva está parametrizada por longitud de arco, considerando que $\|\overline{f}'(s)\|=1$, se tiene que
$$T(s)=\overline{f}'(s)$$

Propiedades del Vector Tangente

(a) En este caso se tiene que
\[
\|T(t)\|= \left\| \frac{f^{\prime}(t)}{\|f^{\prime}(t)\|} \right\|=
\frac{1}{\|f^{\prime}(t)\|} \|f^{\prime}(t)\|=1
\]
por lo tanto $T$ es de magnitud constante.
(b) Tenemos que
\begin{align*} \|T(t)\|=1&\Rightarrow \|T(t)\|^2=1\\&\Rightarrow \frac{d}{dt}\left(\|T(t)\|^2\right)=0\\&\Rightarrow \frac{d}{dt}\left(T(t)\cdot T(t)\right)=0\\&\Rightarrow T'(t)\cdot T(t)+T(t)\cdot T'(t)=0\\&\Rightarrow 2T(t)\cdot T'(t)=0\\&\rightarrow T(t)\cdot T'(t)=0\end{align*}
Esto es $T(t)$ y $T'(t)$ son ortogonales. Este resultado nos permite definir un vector unitario ortogonal a $T(t)$ y que tiene la misma dirección que $T'(t)$.

Vector Normal Principal

Definición. Si $\|T^{\prime}(t)\|\neq 0$ el vector unitario que tiene la misma dirección que $T^{\prime}$ se llama Normal Principal a la curva y se designa por $N(t)$. Asi pues $N(t)$ es una nueva función vectorial asociada a la curva y esta dada por la ecuación:
\[
N(t)=\frac{T^{\prime}(t)}{\|T^{\prime}(t)\|},\ \ \ \ \text{si} \ \ \|T^{\prime}(t)\| \neq 0
\]
Notese que
$$\|N(t)\|=\left\|\frac{T^{\prime}(t)}{\|T^{\prime}(t)\|}\right\|=1$$
Si en la definición anterior, la curva está parametrizada por
longitud de arco, considerando que $T(s)=\overline{f}'(s)$ , se tiene
$$N(s)=\frac{\overline{f}^{\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|}=\frac{T'(s)}{\|T'(s)\|}$$

Vector Binormal

Un tercer vector definido mediante
$$B(t)=T(t)\times N(t)$$
recibe el nombre de Vector binormal.
Notese que $$\|B(t)\|=\|T(t)\times
N(t)\|=\|T(t)\|\|N(t)\|\sin\left(\frac{\pi}{2}\right)=1$$
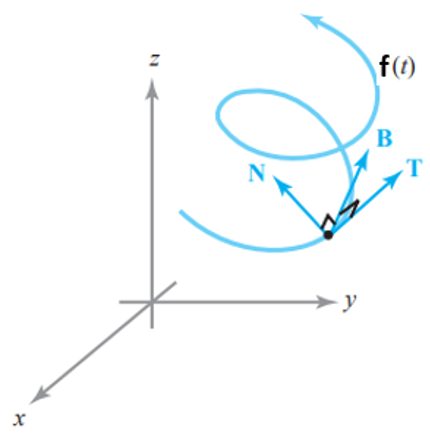
En el punto correspondiente a $f(t)$ en la curva, los vectores $T(t)$, $N(t)$ y $B(t)$ conforman un trío de vectores unitarios y mutuamente ortogonales. Estos dan lugar a un sistema de coordenadas llamado sistema de referencia TNB o sistema de referencia de Frenet-Serret de la curva C.
Los vectores $T(t)$, $N(t)$ y $B(t)$ juegan en el punto de la curva correspondiente a $f(t)$ un papel similar al que juega la tríada i, j y k en el origen del espacio tridimensional. Esta última tríada permace fija, en cambio los vectores $T(t)$, $N(t)$ y $B(t)$ conforman una tríada movil que se mueve a lo largo de la curva.

Ejemplo. Dada la curva $r(t)=\cos t \hat{i}+\sin t \hat{j} + t\hat{k}$ cuya parametrización por longitud de arco es
\[
\bar{r}(s)=\left(\cos\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),\frac{s}{\sqrt{2}}\right)
\]
Hallar los vectores Tangente, Normal y Binormal en un punto $r(s)$.
Solución.

Vector Tangente
\[
T(s)=\frac{f^{\prime}(s)}{\|f^{\prime}(s)\|}=
\left(
-\frac{1}{\sqrt{2}} \sin\left(\frac{s}{\sqrt{2}}\right),
\frac{1}{\sqrt{2}}\cos \left(\frac{s}{\sqrt{2}}\right),
\frac{1}{\sqrt{2}}
\right)
\]
Vector Normal
\[
N(s)=\frac{T^{\prime}(s)}{\|T^{\prime}(s)\|}=
\left(
-\frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right),
-\frac{1}{\sqrt{2}}\left(\frac{1}{\sqrt{2}}\right)\sin\left(\frac{s}{\sqrt{2}}\right),0
\right)
\]
Vector Binormal
\[
B(s)=T(s)\times N(s)=\left|
\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
\frac{-1}{\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\\
-\cos\left(\frac{s}{\sqrt{2}}\right) & -\sin\left(\frac{s}{\sqrt{2}}\right) & 0\\
\end{array}
\right|=
\left(
\frac{1}{\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right),
\frac{-1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right),
\frac{1}{\sqrt{2}}
\right).~~ \blacksquare
\]

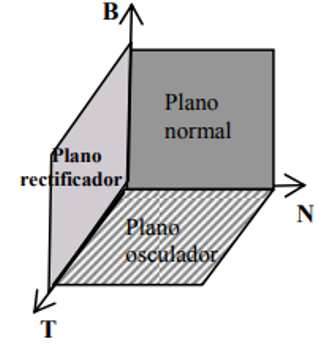
Plano Osculador

Sea $f:[a,b]\rightarrow\mathbb{R}^{3}$ una curva con triada móvil $T(t)$, $N(t)$ y $B(t)$. Sea $P=(x_{0},y_{0},z_{0})$ un punto de la curva f tal que $f(t_{0})=(x_{0},y_{0},z_{0})$. Se llama Plano Osculador de f en el punto P, al plano que pasa por P y es paralelo a los vectores $T(t_{0})$ y $N(t_{0})$. Este plano tiene por ecuación
$$\boxed{B(t_{0})\cdot [(x,y,z)-(x_{0},y_{0},z_{0})]=0}$$ El plano osculador es el plano que mejor se adapta a la curva en cada uno de sus puntos. Si la curva es plana, el plano osculador coincide con el plano de la curva.
Ejemplo. Consideremos la curva $f:\mathbb{R}\rightarrow\mathbb{R}^3$ dado por:
\[ f(s)=\left(
\cos\left(\frac{s}{\sqrt{2}}\right),
\sin\left(\frac{s}{\sqrt{2}}\right),
\frac{s}{\sqrt{2}}
\right)
\]
el cual es dos veces diferenciable parametrizado por longitud de arco y que describe una hélice circular en $\mathbb{R}^3$. Obtenga la ecuación del plano osculador en el punto $f(\sqrt{2}\pi)=(-1,0,\pi)$.
Solución.
Tenemos que:
\[ T(s)=\frac{f^{\prime}(s)}{\|f^{\prime}(s)\|}= \left( -\frac{1}{\sqrt{2}} \sin\left(\frac{s}{\sqrt{2}}\right), \frac{1}{\sqrt{2}}\cos \left(\frac{s}{\sqrt{2}}\right), \frac{1}{\sqrt{2}} \right) \]
y $T(\sqrt{2}\pi)=\left(0,-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$, por otro lado:
\begin{align*}N(s)&=\frac{T^{\prime}(s)}{\|T^{\prime}(s)\|}\\&=\left(
-\frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right),
-\frac{1}{\sqrt{2}}\left(\frac{1}{\sqrt{2}}\right)\sin\left(\frac{s}{\sqrt{2}}\right),0
\right)\\&=\left(
-\left(\frac{1}{2}\right)\cos\left(\frac{s}{\sqrt{2}},\right),-\left(\frac{1}{2}\right)\sin\left(\frac{s}{\sqrt{2}}\right),0
\right)\end{align*}
y $N(\sqrt{2}\pi)=(1,0,0)$.
Por lo que
\[ T(\sqrt{2}\pi)\times N(\sqrt{2}\ \pi) =\left| \begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ \frac{-1}{\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\\-\left(\frac{1}{2}\right)\cos\left(\frac{s}{\sqrt{2}}\right) & -\left(\frac{1}{2}\right)\sin\left(\frac{s}{\sqrt{2}}\right) & 0\\ \end{array}\right|= \left(\frac{1}{2\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right),\frac{-1}{2\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right),\frac{1}{2\sqrt{2}} \right) \]
al evaluar en $\sqrt{2}\ \pi$ nos queda $\displaystyle{\left(0,\frac{1}{2\sqrt{2}},\frac{1}{2\sqrt{2}}\right)}$. Por lo tanto la ecuación del plano osculador en $P=(-1,0,\pi)$ es: \[ (x+1,y,z-\pi)\cdot\left(0,\frac{1}{2\sqrt{2}},\frac{1}{2\sqrt{2}}\right)=0 \] \[ \Rightarrow \frac{1}{2\sqrt{2}} (y) +\frac{1}{2\sqrt{2}} (z-\pi)=0 \] \[ \Rightarrow y+z=\pi.~~ \blacksquare \]

Plano Normal

Se llama Plano Normal de f en el punto P, al plano que pasa por P y es paralelo a los vectores $N(t_{0})$ y $B(t_{0})$. Este plano tiene por ecuación
$$\boxed{T(t_{0})\cdot [(x,y,z)-(x_{0},y_{0},z_{0})]=0}$$
Ejemplo. Consideremos la curva $f:\mathbb{R}\rightarrow
\mathbb{R}^3$ dado por:
\[ f(t)=\left( 2\cos\left(t\right), 2\sin\left(t\right), t \right) \] el cual es dos veces diferenciable y que describe una hélice circular en $\mathbb{R}^3$. Obtenga la ecuación del plano normal en el punto $f\left(\frac{\pi}{2}\right)=\left(0,2,\frac{\pi}{2}\right)$.
Solución. Tenemos que:
\[ T(t)=\frac{1}{\sqrt{5}}\left(-2\sin(t),2\cos(t),1\right) \] y $\displaystyle{T\left(\frac{\pi}{2}\right)=\frac{1}{\sqrt{5}}\left(-2,0,1\right)}$. Por lo tanto la ecuación del plano normal es: \[ \frac{1}{\sqrt{5}}(-2,0,1)\cdot\left[(x,y,z)-\left(0,2,\frac{\pi}{2}\right)\right]=0 \] \[ \Rightarrow 4x-2z+\pi=0.~~\blacksquare \]

Plano Rectificador

Se llama Plano rectificador de f en el punto P, al plano que pasa por P y es paralelo a los vectores $T(t_{0})$ y $B(t_{0})$. Este plano tiene por ecuación
$$\boxed{N(t_{0})\cdot [(x,y,z)-(x_{0},y_{0},z_{0})]=0}$$
Ejemplo. Consideremos la curva $f:\mathbb{R}\rightarrow \mathbb{R}^3$ dada por:
\[ f(t)=\left( 2\cos\left(t\right), 2\sin\left(t\right), t \right) \] la cual es dos veces diferenciable y que describe una hélice circular en $\mathbb{R}^3$. Obtenga la ecuación del plano rectificador en el punto $\displaystyle{f\left(\frac{\pi}{2}\right)=\left(0,2,\frac{\pi}{2}\right)}$.
Solución. Tenemos que: \[ N(t)=\left(-\cos(t),-\sin(t),0\right) \] y $\displaystyle{N\left(\frac{\pi}{2}\right)=\left(0,-1,0\right)}$. Por lo tanto la ecuación del plano rectificador es: \[ (0,-1,0)\cdot\left[(x,y,z)-\left(0,2,\frac{\pi}{2}\right)\right]=0 \] \[ \Rightarrow y-2=0.~~\blacksquare \]

Mas adelante

En la siguiente entrada veremos como a partir de vectores caracterizados en esta entrada podemos definir y calcular la curvatura y radio de curvatura de una curva o plano.

Tarea Moral

1.- Determina $T$ y $N$ para cada una de las siguientes curvas:

La parábola $x=pt^2$ , $y=2pt$.

La elipse $f(\theta)=(acos\theta, b sen\theta)$, $\theta \in [0,2\pi]$; $a,b>0$

2.- Si una curva está descrita por $f(t)= (t,t^2,t^3)$, determína $T(t)$, $N(t)$, $B(t)$ y el plano osculador cuando $t=0$ y $t=1$

3.- Si $C$ es una curva en $R^3$ descrita por $f$ demuestra que

$B=\dfrac{f’ \times f^{‘ ‘}}{|f’ \times f^{‘ ‘} |}$, $N=B \times T= \dfrac{(f’ \times f^{‘ ‘})\times f’}{| (f’ \times f^{‘ ‘} \times f’)|}$

4.- Demuestra que si una curva $C$ se encuentra en el plano $P$ en $R^3$ entonces el plano osculador en cualquier punto de $C$ es $P$.

5.- Determina $T,N$ y $B$ y el plano osculador en $f(0)$ para las curvas en seguida descritas.

a) $f(t)= (t cost, t sent, t)$

b) $f(t)= (t-sent, 1-cost, t)$

Introducción

Definición. Si C es un arco de curva rectificable, definimos su longitud $L(C)$ como la suma
$$\boxed{L_{C}=\sup{s(P)}=\sup\left\{\Sigma\|f(t_{k})-f(t_{k-1})\|\right\}}$$
Ahora vamos a obtener una fórmula para la longitud de arco.
Sea $\overline{\alpha}:[a,b]\rightarrow \mathbb{R}^{2}$ ó $\mathbb{R}^{3}$, continua en $[a,b]$, derivable en (a,b) y $\overline{\alpha^{\prime}}(t)\neq 0$ para todo $t\in [a,b]$ y sea $P={t_{0},t_{1},…,t_{n}}$ una partición de $[a,b]$

entonces según la figura se tiene que
$$\ell(\overline{\alpha})\approx \sum_{i=1}^{n}\|\alpha(t_{i})-\alpha(t_{i-1})\|=\sum_{i=1}^{n}\sqrt{\left[\alpha_{1}(t_{i})-\alpha_{1}(t_{i-1})\right]^{2}+…+\left[\alpha_{n}(t_{i})-\alpha_{n}(t_{i-1})\right]^{2}}$$
Aplicando el teorema del valor medio en cada subintervalo $[t_{i-1},t_{i}]$ tenemos que
$$\frac{\alpha_{i}(t_{i})-\alpha_{i}(t_{i-1})}{t_{i}-t_{i-1}}=\alpha^{\prime}(t^*),~~~t^*\in(t_{i-1},t_{i})$$
se tiene que
\begin{align*}&\sum_{i=1}^{n}\sqrt{\left[\alpha_{1}(t_{i})-\alpha_{1}(t_{i-1})\right]^{2}+…+\left[\alpha_{n}(t_{i})-\alpha_{n}(t_{i-1})\right]^{2}}=\\&\sum_{i=1}^{n}\sqrt{\left[\alpha_{1}^{\prime}(t_{1})(t_{i}-t_{i-1})\right]^{2}+…+\left[\alpha_{n}^{\prime}(t_{n})(t_{i}-t_{i-1})\right]^{2}}=\\&\sum_{i=1}^{n}(t_{i}-t_{i-1})\sqrt{\left[\alpha_{1}^{\prime}(t_{1})\right]^{2}+…+\left[\alpha_{n}^{\prime}(t_{n})\right]^{2}}=\\&\sum_{i=1}^{n}(t_{i}-t_{i-1})\sqrt{\left[\alpha_{1}^{\prime}(t_{1})\right]^{2}+…+\left[\alpha_{n}^{\prime}(t_{n})\right]^{2}}=\\&\sum_{i=1}^{n}(t_{i}-t_{i-1})\sqrt{\left[\alpha_{1}^{\prime}(t)\right]^{2}+…+\left[\alpha_{n}^{\prime}(t)\right]^{2}}=\\&\sum_{i=1}^{n}\|\alpha^{\prime}(t^*)\|(t_{i}-t_{i-1})\\&Si~{n\rightarrow \infty}~~entonces~~\sum_{i=1}^{n}\|\alpha^{\prime}(t^*)\|(t_{i}-t_{i-1})\rightarrow \int_{a}^{b}\|\alpha^{\prime}(t)\|~dt\end{align*}
Definición. Sea $f:I\subset \mathbb{R}\rightarrow \mathbb{R}^{2}$ ó $\mathbb{R}^{3}$ una curva parametrizable. Sean $a,b\in I$ con $a<b$. Para cualquier partición $P={t_{0},…,t_{n}}$ del intervalo $[a,b]$ definimos
$$sup\left\{\sum_{i=1}^{n}\|\alpha^{\prime}(t)\|(t_{i}-t_{i-1})\right\}=\int_{a}^{b}\|\alpha^{\prime}(t)\|~dt$$
curva o la longitud de arco de la curva en caso de que la integral exista.
Ejemplo. Calcular la longitud de arco de $\sigma(t)=(rt-r\sin(t),r-r\cos(t))$. En este caso
tenemos que $\sigma^{\prime}=(r-r\cos(t),r\sin(t))$ para $t\in[0,2\pi]$ $\therefore$ la longitud de arco es:
\begin{align*} \int_{0}^{2\pi}\sqrt{(r-r\cos(t))^{2}+(r\sin(t))^{2}} &=\int_{0}^{2\pi}\sqrt{r^{2}-2r^{2}\cos(t)+r^{2}\cos^{2}(t)+r^{2}\sin^{2}(t)}dt \\ &=\int_{0}^{2\pi}\sqrt{2r^{2}-2r^{2}\cos(t)}dt \\ &=\sqrt{2}r\int_{0}^{2\pi}\sqrt{1-\cos(t)}dt\\ &=\sqrt{2}r\int_{0}^{2\pi}\sqrt{2}\sin\left(\frac{t}{2}\right)dt\\&=2r\int_{0}^{2\pi}\sin\left(\frac{t}{2}\right)dt \\ &=2r\left(2\cdot\left(-\cos\left(\frac{t}{2}\right)\right|_{0}^{2\pi}\right) \\ &=8r.~ \blacksquare \end{align*}

Reparametrización de curvas

Consideremos la curva $f:[-1,1]\rightarrow \mathbb{R}^{2}$
dada por $f(t)=(-t,\sqrt{1-t^{2}})$ la cual describe un arco de la
circunferencia $x^{2}+y^{2}=1$ entre -1 y 1.

Sea $\overline{f}:[0,\pi]\rightarrow[0,1]$ la función $\overline{f}(s)=[\cos(s),\sin(s)]$

Si definimos una función $\varphi:[0,\pi]\rightarrow[-1,1]$ dada por $\varphi(s)=-cos(s)$ tenemos que $\overline{f}=f\circ\varphi$, es decir
$$\overline{f}(s)=f\circ \varphi(s)=f(\varphi(s))=f(-cos(s))=[-(-cos(s)),\sqrt{1-(-\cos(s))^{2}}]=[cos(s),\sin(s)]$$

Decimos que $\overline{f}$ es una reparametrización de $f$.$~~\blacksquare$
Definición. Sea $f:[a,b]\subset\mathbb{R}^{n}$ una curva con derivada distinta de cero. Sea $\varphi:[c,d]\rightarrow[a,b]$ una función con derivada continua sobreyectiva tal que $\varphi’\neq0$ $\forall s\in [a,b]$. Entonces la curva $\overline{f}=f\circ\varphi:[c,d]\rightarrow\mathbb{R}^{n}$ se llama reparametrización de la curva f.
Nota:
La condición $\varphi’\neq0$ nos conduce a $\varphi’>0$ o $\varphi'<0$. Si $\varphi’>0$ entonces $\varphi$ es una función creciente en [c,d] de modo que $\varphi(c)=a$ y $\varphi(d)=b$ y asi los puntos inicial y final de $\overline{f}$ coinciden con los respectivos de f$$\overline{f}(c)=f\circ\varphi(c)=f(\varphi(c))=f(a)~~~y~~~ \overline{f}(d)=f\circ\varphi(d)=f(\varphi(d))=f(b)$$
como $\overline{f}'(s)=\varphi'(s)f'(\varphi(s))$ entonces $f’$ y $\overline{f}’$ tienen la misma dirección y en este caso como $\varphi’~>0$, entonces, el camino en el que $\overline{f}$ recorre la curva descrita por f es en la misma dirección. Por lo tanto diremos que $\overline{f}$ es una reparametrización de f que conserva la orientación.
Ejemplo. Obtenga una reparametrización de la curva $f:[0,2]\rightarrow\mathbb{R}^{2}$ dada por $f(t)=(3t+2,t^{3}+3)$.
Solución. Proponemos la función $t=\varphi(s)=2s$, en la cual se tiene $\varphi'(s)=2>0$,
es decir si su derivada es constante, entonces no se anula para ningun valor. Ahora bien si $t=0\Rightarrow s=0$ y $t=2\Rightarrow s=1$ por lo tanto $\varphi:[0,1]\rightarrow[0,2]$ mientras que
$$\overline{f}(s)=f(\varphi(s))=f(2s)=(3(2s)+2,(2s)^{3}+3)=(6s+2,8s^{3}+3)\quad
s\in[0,1]$$ tenemos entonces que $\overline{f}$ es una reparametrización de f. Vamos a comprobar que representan el mismo lugar geométrico. Para $f(t)$ se tiene $\displaystyle{x=3t+2\rightarrow t=\frac{x-2}{3}}$ y si $y=t^{3}+3$ entonces $\displaystyle{y=\left(\frac{x-2}{3}\right)^{3}+3}$ mientras que para $\overline{f}(s)$, $\displaystyle{x=6s+2\rightarrow s=\frac{x-2}{6}}$ por tanto si $y=8s^{3}+3$ entonces $\displaystyle{y=8\left(\frac{x-2}{6}\right)^{3}+3}$ por lo que igualando coordenadas de cada representación paramétrica, se tiene$$\left(\frac{x-2}{3}\right)^{3}+3=8\left(\frac{x-2}{6}\right)^{3}+3\Rightarrow \frac{1}{3^{3}}=\frac{8}{6^{3}}$$ lo cual es cierto y por lo tanto representan el mismo lugar geometrico.$~~\blacksquare$
Proposición. Supongamos que $f:[a,b]\rightarrow\mathbb{R}^{n}$ es una curva con $f’\neq 0$ y que $\overline{f}:[c,d]\rightarrow\mathbb{R}^{n}$ es una reparametrización de f. Entonces
$$\int_{a}^{b}\|f'(t)\|~dt=\int_{c}^{d}\|\overline{f}'(s)\|~ds$$
Demostración. Tenemos que $\overline{f}=f\circ \varphi$, donde $\varphi:[c,d]\rightarrow[a,b]$ es de clase $c^{1}$, biyectiva y $\varphi’\neq 0~~\forall~s\in [c,d]$. Entonces
\begin{align*} L(\overline{f}) &=\int_{c}^{d}|\overline{f}'(s)|~ds \\ &=\int_{c}^{d}\|\varphi'(s)f'(\varphi(s))\|~ds \\ &=\int_{c}^{d}\|\overline{f}'(\varphi(s))\|~|\varphi'(s)|~ds~~~(si~\varphi’>0)\\
&=\int_{c}^{d}\|\overline{f}'(\varphi(s))\|~\varphi'(s)~ds \\
&=\int_{a}^{b}\|f'(t)\|~dt,~~(t=\varphi(s),~~dt=\varphi'(s)~ds) \\
&=L(f).~~ \blacksquare \end{align*}

Función Longitud de Arco

A continuación introducimos la función longitud de arco de una curva. Esta función nos permitirá prporcionar una nueva reparametrización de una curva, lo cual será de gran
utilidad más adelante.
Definición. Sea $f:[a,b]\rightarrow\mathbb{R}^{n}$ una curva de longitud L. Se llama función longitud de arco de la curva $f(t)$ a la función $s:[a,b]\rightarrow[0,L]$ dada por
$$s(t)=\int_{a}^{t}\|f'(u)\|~du$$
$s(t)$ es la longitud del arco entre los puntos $P_{0}$ y $P$, que son los puntos terminales de $f(a)$ y $f(t)$

Ejemplo. Hallar la función longitud de arco de la hélice $f(t)=(\cos(t),\sin(t),t),~~t\in[0,2\pi]$.
Solución. En este caso tenemos que
\begin{align*} f'(t) & =(-\sin(t),\cos(t),1) \\ |f'(t)| & =\sqrt{(-\sin(t))^{2}+(\cos(t))^{2}+1^{2}}=\sqrt{2} \end{align*}
Ahora, para $t\in[0,2\pi]$ tenemos
$$s(t)=\int_{0}^{t}\|f'(u)\|~du=\int_{0}^{t}\sqrt{2}~du=\sqrt{2}t$$
Si $t\in[0,2\pi]$ entonces
\begin{align*} s(0)&=0\\s(2\pi)&=2\pi\sqrt{2}\end{align*}
Luego, la función longitud de arco $s:[0,2\pi]\rightarrow[0,2\pi\sqrt{2}]$ de esta porción de hélice es
$$s(t)=\sqrt{2}t.~~ \blacksquare$$

Reparametrización por Longitud de Arco

Entre las muchas reparametrizaciones de una curva contamos con una que está muy relacionada con las características geométricas de la curva y además, posee propiedades importantes. Esta es la reparametrización por longitud de arco, la que se obtiene mediante la función de longitud de arco.
Sea $f:[a,b]\rightarrow\mathbb{R}^{n}$ una curva diferenciable. Para reparametrizarla por longitud de arco se siguen los siguientes pasos:
(a) Hallar la función longitud de arco de la curva:
$$s:[a,b]\rightarrow[0,L],~~~\displaystyle{s(t)=\int_{a}^{t}\|f'(u)\|~du}$$
(b) Hallar la función inversa de la función longitud de arco:
$$\varphi=s^{-1}:[0,L]\rightarrow[a,b]$$
La reparametrización por longitud de arco de la curva $f:[a,b]\rightarrow\mathbb{R}^{n}$ es
$$\overline{f}=f\circ \varphi:[0,L]\rightarrow\mathbb{R}^{n}$$
Ejemplo. Sea $f(t)=(r \cos t , r\sin t)$ con $t\in[0,2\pi]$. Obtengamos su reparametrizacion por longitud de arco.
Solución.
(a) Hallamos la función longitud de arco s(t) que en éste caso es:
$$f'(t)=(-r\sin(t),r\cos(t))~~y~~\|f'(t)\|=\sqrt{(-r\sin(t))^{2}+(r\cos(t))^{2}}=r$$
$s:[0,2\pi]\rightarrow[0,2\pi r]$, $\displaystyle{s(t)=\int_{0}^{t}\|f'(u)\|~du=\int_{0}^{t}r~du=rt}$ esto es
$$s(t)=rt$$
Si $t\in[0,2\pi]$ entonces
\begin{align*}s(0)&=0\\s(2\pi)&=2\pi r\end{align*}
Por lo que $s\in[0,2\pi r]$
(b) Hallamos la función inversa de la longitud de arco
$$\varphi=s^{-1}:[0,2\pi r]\rightarrow[0,2\pi]$$
Sea $s=s(t)$. Entonces $s=rt$, por lo tanto despejando t tenemos $\displaystyle{t=\frac{s}{r}}$. Luego
$$t=\varphi(s)=s^{-1}=\frac{s}{r}$$
Por lo tanto la reparametrización buscada es
$$\overline{f}(s)=f\circ \varphi(s)=f\left(\varphi(s)\right)=f\left(\frac{s}{r}\right)=\left(r\cos
\left(\frac{s}{r}\right),r\sin\left(\frac{s}{r}\right)\right)~~\blacksquare$$
Observación.
En el ejemplo anterior notamos que:
$$\|\overline{f}^{\prime}(s)\|=
\left\|-r\sin\left(\frac{s}{r}\right)\frac{1}{r},r\cos \left(\frac{s}{r}\right)\frac{1}{r}\right\|=
\left\|-\sin\left(\frac{s}{r}\right),\cos\left(\frac{s}{r}\right)\right\|=1$$

Ejemplo. Sea $f(t)=(\cos t , \sin t,t),~~t\in[0,2\pi]$ . Obtengamos la reparametrizacion por la longitud de arco.
Solución.
(a) Hallamos la función longitud de arco s(t), que en éste caso es:
$$f'(t)=(-\sin(t),\cos(t),1)~~y~~\|f'(t)\|=\sqrt{(\sin(t))^{2}+(\cos(t))^{2}+1^{2}}=\sqrt{2}$$
Si $t\in[0,2\pi]$ entonces $s:[0,2\pi]\rightarrow[0,2\pi \sqrt{2}]$, por lo que$\displaystyle{s(t)=\int_{0}^{t}\|f'(u)\|~du=\int_{0}^{t}\sqrt{2}~du=\sqrt{2}t}$ esto es
$$s(t)=\sqrt{2}t$$
Hallamos la función inversa de la longitud de arco
$$\varphi=s^{-1}:[0,2\pi \sqrt{2}]\rightarrow[0,2\pi]$$
Sea $s=s(t)$. Entonces $s=\sqrt{2}t$, por lo tanto despejando t tenemos $\displaystyle{t=\frac{s}{\sqrt{2}}}$. Luego
$$t=\varphi(s)=s^{-1}=\frac{s}{\sqrt{2}}$$
y la reparametrización buscada es
$$\overline{f}(s)=f\circ h(s)=f\left(h(s)\right)=f\left(\frac{s}{\sqrt{2}}\right)=\left(r\cos
\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),\frac{s}{\sqrt{2}}\right),~~s\in[0,2\pi \sqrt{2}] \blacksquare$$

La reparametrización por longitud de arco tiene rapidez constante

Sabemos que si $\textbf{s}:[a,b]\rightarrow [c,d]$ es una función de clase $c^{1}$ tal que $\textbf{s}’\neq 0~~\forall~t\in[a,b]$, también se tiene $\textbf{s}^{-1}:[c,d]\rightarrow [a,b]$ es tal que $(\textbf{s}^{-1})’$ es de clase $c^{1}$.
Observamos que la función $\varphi=\textbf{s}^{-1}:[c,d]\rightarrow [a,b]$ tiene entonces las características que se necesitan para que $\overline{f}=f\circ \varphi$ sea una reparametrización de f.

Tenemos que para $s\in [c,d]$
$$\overline{f}(s)=(f\circ\varphi)(s)=f(\varphi(s))$$
por lo que
$$\overline{f}'(s)=(f\circ\varphi)'(s)=f'(\varphi(s))\varphi'(s)$$
Pero
$$\varphi'(s)=(\textbf{s}^{-1})'(s)=\frac{1}{\textbf{s}'(\textbf{s}^{-1}(s))}=\frac{1}{\textbf{s}'(\varphi(s))}=\frac{1}{\|f'(\varphi(s))\|}$$
Por lo tanto
$$\|\overline{f}'(s)\|=\|f'(\varphi(s))\varphi'(s)\|=\left\|f'(\varphi(s))\cdot\frac{1}{\|f'(\varphi(s))\|} \right\|=\|f'(\varphi(s))\|\cdot\frac{1}{\|f'(\varphi(s))\|}=1~~ \blacksquare$$

Propiedad de la reparametrización por longitud constante

Si $\overline{f}$ es una reparametrización de f tal que $\|\overline{f}(t)\|=1$ para toda $t\in [a,b]$ entonces
$$L(\overline{f})=\int_{a}^{b}\|\overline{f}(t)\|~dt=\int_{a}^{b}~dt=b-a$$
Por lo que $\overline{f}$ es una reparametrización tal que la longitud que describe es igual al tiempo que tarda en recorrerla.$~\blacksquare$

Más adelante

Tarea Moral

1.- Aporta una parametrización al cuadrado unitario de $\mathbb{R}^2$ con vértices en los puntos: (0,0), (1,0), (1,1), (0,1).

2.- Determina la longitud de arco de la parábola descrita por $f(t)=(t^2,2t)$, $t\in [0,1]$

3.- Determina la longitud de la gráfica de $y=ln(1-x^2)$ entre $x=0$ y $x=\dfrac{1}{2}$

4.- La gráfica polar de $r=1+cos\theta$ es una cardioide y sus ecuaciones paramétricas son: $x=(1+cos\theta)cos\theta$, $y=(1+cos\theta) sen\theta $, $\theta \in [0,2\pi]$. Determina su longitud de arco.

5.- Encuentra una reparametrización de la elipse $r(t)=(acost, bsent)$, $t\in [0,2\pi]$ y determina su reparametrización por longitud de arco.

Introducción

La longitud de una curva como una integral nos permite estudiarla analíticamente. Recordemos que en cálculo el estudio de ciertos objetos matemáticos se hacen a partir de una aproximación. En este caso la noción intuitiva será: la longitud de una curva será el límite de longitudes de polígonos aproximados. Esta longitud estará definida como una integral.

Definición. Una arco de curva esta dado por una función vectorial $f:[a,b]\rightarrow\mathbb{R}^{n}$. Donde el dominio esta restringido al intervalo cerrado $[a,b]\in\mathbb{R}$.
Definición. Sea C un arco de curva en $\mathbb{R}^{n}$ dada por la función
$$f(t)=(f_{1}(t),f_{2}(t),…,f_{n}(t))$$
Consideremos el conjunto
$$P=\{P~\Big{|}~P~es~partici\acute{o}n~de~[a,b]\}$$
Para cada partición $P:~a=t_{0},t_{1},…,t_{n-1},t_{n}=b$ de $[a,b]$ consideramos la poligonal
$$f(t_{0}),f(t_{2}),…,f(t_{n-1}),f(t_{n})$$
y su correspondiente longitud
$$s(P)=|f(t_{1})-f(t_{0})|+|f(t_{2})-f(t_{1})|+\cdots+|f(t_{n-1})-f(t_{n})|=\sum_{i=1}^{n}||f(t_{i})-f(t_{i-1})||$$
Se dice C es rectificable si el conjunto ${s(P)}$ esta acotado.

Ejemplo. Muestre que el arco de parábola C dado por $f(t)=(t,t^{2})$ con $t\in(0,1)$ es rectificable.
En este caso sea $P\in[0,1]$ dada por $0=t_{0}<t_{1}<\cdots<t_{n}=1$. Tenemos entonces
\begin{align*} s(P) & =\sum_{i=1}^{n}|f(t_{i})-f(t_{i-1})| \\ & =\sum_{i=1}^{n}|(t_{i},t_{i}^{2})-(t_{i-1},t_{i-1}^{2})| \\ &=\sum_{i=1}^{n}|(t_{i}-t_{i-1},t_{i}^{2}-t_{i-1}^{2})| \\ & \leq \sum_{i=1}^{n}|t_{i}-t_{i-1}|+|t_{i}^{2}-t_{i-1}^{2}| \\ &=\sum_{i=1}^{n}|t_{i}-t_{i-1}|+|(t_{i}-t_{i-1}|~|(t_{i}+t_{i-1}|\\ &=\sum_{i=1}^{n}(t_{i}-t_{i-1})(1+(t_{i}-t_{i-1})~~\textcolor{red}{Si~0\leq t_{i-1}\leq t_{1}\leq 1~entonces~1+t_{i-1}+t_{i}\leq 3}\\ &\leq 3\sum_{i=1}^{n}(t_{i}-t_{i-1})\\ &\leq 3 \end{align*}
esto quiere decir que la suma $s(P)$ es acotada y por lo tanto, el arco es rectificable.$~~ \blacksquare$
Ejemplo. Mostrar que la siguiente función vectorial (curva) $f:[0,1]\rightarrow\mathbb{R}^{2}$ dada por $\displaystyle{f(t)=\left[t,t\cos\left(\frac{1}{t}\right)\right]}$ donde $f(0)=(0,0)$ no es rectificable.
En este caso consideramos particiones de $[0,1]$ de la forma
$$P:t_{0}=0,t_{1}=\frac{1}{(n-1)\pi},t_{2}=\frac{1}{(n-2)\pi},…,t_{n-2}=\frac{1}{2\pi},t_{n-1}\frac{1}{\pi},t_{n}=1$$
Los puntos de la poligonal que corresponden a la partición P son
$$f(t_{0})=(0,0),f(t_{1})=\left(\frac{1}{(n-1)\pi},\frac{1}{(n-1)\pi}\cos((n-1)\pi)\right),f(t_{2})=\left(\frac{1}{(n-2)\pi},\frac{1}{(n-2)\pi}\cos((n-2)\pi)\right),…$$
$$,f(t_{n-2})=\left(\frac{1}{2\pi},\frac{1}{2\pi}\cos(2\pi)\right),f(t_{n-1})=\left(\frac{1}{\pi},\frac{1}{\pi}\cos(\pi)\right),f(t_{n})=(1,\cos(1))$$
La suma de las distancias de los segmentos de la poligonal es
\begin{align*} s(P)&=|f(t_{1})-f(t_{0})|+|f(t_{2})-f(t_{1})|+\cdots|f(t_{n})-f(t_{n-1})| \\ &=\left|\left(\frac{1}{(n-1)\pi},\frac{1}{(n-1)\pi}\cos((n-1)\pi)\right)\right| \\ &+\left|\left(\frac{1}{(n-2)\pi}-\frac{1}{(n-1)\pi},\frac{1}{(n-2)\pi}\cos((n-2)\pi)-\frac{1}{(n-1)\pi}\cos((n-1)\pi)\right)\right| \\ &+\cdots+\left|\left(1-\frac{1}{\pi},\cos(1)-\frac{1}{\pi}\cos(\pi)\right)\right| \\ &\geq \sum_{k=1}^{n-2}\left|\left(\frac{1}{k\pi}-\frac{1}{(k+1)\pi},\frac{1}{k\pi}\cos(k\pi)-\frac{1}{(k+1)\pi}\cos((k+1)\pi)\right)\right| \\ &\geq \sum_{k=1}^{n-2}\left|\frac{1}{k\pi}\cos(k\pi)-\frac{1}{(k+1)\pi}\cos((k+1)\pi)\right|\\ &\geq \sum_{k=1}^{n-2}\left|\frac{(-1)^{k}}{k\pi}-\frac{(-1)^{k+1}}{(k+1)\pi}\right|\\ &=\sum_{k=1}^{n-2}\left|\frac{1}{k\pi}+\frac{1}{(k+1)\pi}\right|\\ &\geq \frac{2}{\pi}\sum_{k=1}^{n-2}\frac{1}{k+1} \end{align*}
Entonces,
$$\lim_{n\rightarrow\infty}s(P)\geq \lim_{n\rightarrow\infty}\frac{2}{\pi}\sum_{k=1}^{n-2}\frac{1}{k+1}=+\infty$$
lo cual implica que la suma $s(P)$ no es acotada y por lo tanto el arco de curva no es rectificable.$~~ \blacksquare$
Teorema. [Criterio para determinar si una curva es rectificable]
Todo arco de curva de clase $C^{1}$ (con derivada continua) es rectificable.
Demostración.Sea $f(t)=(f_{1}(t),f_{2}(t),…,f_{n}(t))$ un arco de curva de clase $C^{1}$. Entonces, las funciones $f'{i}$ son continuas en $[a,b]$ y por tanto estan acotadas es decir, existen constantes positivas $M{1},…,M_{n}$ tales que
$$|f'{1}(t)|\leq M{1},…,|f'{n}(t)|\leq M{n}~~~\forall~t\in[a,b]$$
Sea P una partición del intervalo $[a,b]$ determinada por los puntos $a=t_{0}<t_{1}<\cdots<t_{n}=b$. Para cada $i\in{1,2,…,n}$ tenemos
\begin{align*} \|f(t_{i})-f(t_{i-1})\|&=\sqrt{\sum_{j=1}^{n}\left(f_{j}(t_{i})-f_{j}(t_{i-1})\right)^{2}} \\ &\leq \sum_{j=1}^{n}\left|f_{j}(t_{i})-f_{j}(t_{i-1})\right| \end{align*}
Por el teorema del valor medio de Lagrange, existen $\xi_{1},\xi_{2},…,\xi_{n}$ en el intervalo $(t_{i-1},t_{i})$ tales que
\begin{align*} \left|f_{1}(t_{i})-f_{1}(t_{i-1})\right| &= |f'{1}(\xi{1})|(t_{i}-t_{i-1}) \\
\vdots & =\vdots \\
\left|f_{n}(t_{i})-f_{n}(t_{i-1})\right| &= |f'{n}(\xi{1})|(t_{i}-t_{i-1})
\end{align*}
En consecuencia,
\begin{align*} \|f(t_{i})-f(t_{i-1})\|&\leq \left|f_{1}(t_{i})-f_{1}(t_{i-1})\right|+\cdots +\left|f_{n}(t_{i})-f_{n}(t_{i-1})\right| \\ & \leq \left(|f'{1}(\xi{1})|+\cdots+|f'{n}(\xi{1})|\right)(t_{i}-t_{i-1})\\
&\leq (M_{1}+\cdots+ M_{n})(t_{i}-t_{i-1}).
\end{align*}
Si $s(P)$ es la longitud de la poligonal determinada por P tenemos
\begin{align*} s(P)&=\sum_{i=1}^{n}\|f(t_{i})-f(t_{i-1})\| \\ &\leq (M_{1}+\cdots+ M_{n})\sum_{i=1}^{n}(t_{i}-t_{i-1}) \\ &=(M_{1}+\cdots+ M_{n})(b-a). \end{align*}
Es decir, el conjunto ${s(P)}$ con P partición de $[a,b]$ está acotado y por tanto el arco de curva es rectificable.$ \blacksquare$
Ejemplo. Muestre que el arco de curva C dado por $f(t)=(t,t^{3})$ con $t\in(0,1)$ es rectificable.
En este caso $f'(t)=(1,3t^{2})$, cada función componente es continua y por tanto $f(t)$ es de clase $C^{1}$ por lo que según el resultado anterior, se tiene que f es rectificable en el intervalo indicado.$~~\blacksquare$

Más adelante

En esta sección vimos cómo aproximar la longitud de arco de una función vectorial con dominio acotado mediante el cálculo de las longitudes de polígonos. En la siguiente sección definiremos el cálculo de la longitud de arco, el cual, está determinado mediante una integral.

Tarea Moral

1.- Prueba que la curva definida como $y=\begin{cases}x^{2}sen\dfrac{1}{x},0< x\leq 1\\ 0,x=0\end{cases}$ tiene longitud finita.

2.- Prueba que $y=\begin{cases}xsen\dfrac{1}{x},0< x\leq 1\\ 0,x=0\end{cases}$ no es rectificable.

3.- Prueba que si una función f es deinida y monótona en el intervalo cerrado $[a,b]$ entonces el arco de curva definido como $y=f(x)$, $(a\leq x \leq b)$ es rectificable.

4.- Muestra que la siguiente función $\gamma :A=\left[ 0,2\pi \right] \rightarrow \mathbb{R}$ dada por $\gamma(t)=\dfrac{3}{2}(cos(t), sint(t))$ es rectificable.

5.- Propón una función vectorial cuyo arco de curva sea rectificable y una donde no lo sea.

Introducción

Generalizando un poco las ideas del cálculo diferencial de funciones $f:\mathbb{R}\rightarrow \mathbb{R}$ a funciones $f:\mathbb{R}\rightarrow \mathbb{R}^{n}$. Recordemos que $f:\mathbb{R}\rightarrow \mathbb{R}$ es diferenciable en un punto $t_{0}$ si
$$\lim_{h\rightarrow 0}\frac{f(t_{0}+h)-f(t_{0})}{h}$$existe y en tal caso lo denotamos $f'(t_{0})$

Definición. Sea $r:I\subset\mathbb{R}\rightarrow \mathbb{R}^{n}$ una función vectorial definida en un intervalo abierto $I\in\mathbb{R}$ y $t\in I$. Se define la derivada de f en $t$, denotada por $r'(t)$ como
$$r'(t)=\lim_{h\rightarrow 0}\frac{r(t+h)-r(t)}{h}$$cuando este limite existe

Ejemplo. Usa la definición para calcular la derivada de la función.
$$r(t)=(3t+4)i+(t^{2}-4t+3)j$$

Tenemos que
$$r'(t)=\lim_{h\rightarrow0}\frac{r(t+h)-r(t)}{h}$$
$$=\lim_{h\rightarrow0}\frac{[(3(t+h)+4)i+((t+h)^{2}-4(t+h)+3)j]-[(3t+4)i+(t^{2}-4t+3)j]}{h}$$
$$=\lim_{h\rightarrow0}\frac{(3t+3h+4)i-(3t+4)i+(t^{2}+2th+h^{2}-4t-4h+3)j-(t^{2}-4t+3)j}{h}$$
$$=\lim_{h\rightarrow0}(3i+(2th+h-4)j)$$
$$=3i+(2t-4)j.~~ \blacksquare$$

Teorema. Sea $f:\mathbb{R} \rightarrow \mathbb{R}^{n}$ una función vectorial, $t_{0}\in \mathbb{R}$. f es diferenciable en el punto $t_{0}$ si y solo si cada función componente $x_{i}(t)$ de f es diferenciable en el punto $t_{0}$, en cuyo caso $$f'(t_{0})=(x’_{1}(t_{0}),x’_{2}(t_{0}),..,x’_{n}(t_{0}))$$

Demostración. $(\textcolor{red}{\Rightarrow})$
Supongamos que f es diferenciable en $t_{0}$. Entonces

$$\lim_{h\rightarrow 0}\frac{f(t_{0}+h)-f(t_{0})}{h}$$

Por otro lado

$$\lim_{h\rightarrow 0}\frac{f(t_{0}+h)-f(t_{0})}{h}=\lim_{h\rightarrow 0}\left(\frac{(x_{1}(t_{0}+h),x_{2}(t_{0}+h),…,x_{n}(t_{0}+h))-(x_{1}(t_{0}),x_{2}(t_{0}),…,x_{n}(t_{0}))}{h}\right)$$
$$=\lim_{h\rightarrow 0}\left(\frac{x_{1}(t_{0}+h)-x_{1}(t_{0})}{h},\frac{x_{2}(t_{0}+h)-x_{2}(t_{0})}{h},…,\frac{x_{n}(t_{0}+h)-x_{n}(t_{0})}{h}\right)$$
$$=\left(\lim_{h\rightarrow 0}\frac{x_{1}(t_{0}+h)-x_{1}(t_{0})}{h},\lim_{h\rightarrow 0}\frac{x_{2}(t_{0}+h)-x_{2}(t_{0})}{h},…,\lim_{h\rightarrow 0}\frac{x_{n}(t_{0}+h)-x_{n}(t_{0})}{h}\right)$$
conforme $h\rightarrow 0$ cada limite de las funciónes componentes existe $\therefore$
$$\lim_{h\rightarrow 0}\frac{x_{i}(t_{0}+h)-x_{i}(t_{0})}{h}=x’_{i}(t_{0})$$
$\therefore$ cada $x_{i}$ es diferenciable en $t_{0}$

$(\textcolor{red}{\Leftarrow})$ Se pueden regresar en los pasos de la prueba anterior.$~~ \blacksquare$
Definición. La derivada $f'(t)$ de una trayectoria f puede ser asociada a una matriz $n\times 1$ la cual es conocida como la matriz Jacobiana de f en el punto $t_{0}$.

Se denota
$$Jf(t_{0})=\left[\begin{matrix}x’_{1}(t_{0})\\x’_{2}(t_{0})\\\vdots\\x’_{n}(t_{0})\end{matrix}\right]$$

Propiedades de la derivada de funciones con valores vectoriales

Ejercicio. Utiliza la definición de derivada para demostrar que:
Si $f:\mathbb{R}\rightarrow \mathbb{R}^{n}$ esta dada por $f(t)=a\in\mathbb{R}^{n}$, $a$ constante, entonces $f'(t)=0$
Solución.
$$f'(t)=\lim_{h \rightarrow 0}\frac{f(t+h) – f(t)}{h}=
\lim_{h \rightarrow 0} \frac{a-a}{h} = 0.~~ \blacksquare$$
Ejercicio. Prueba lo siguiente: Si $f(t)=ah(t)$ entonces $f'(t)=ah'(t)$
Solución.
\[\begin{array}{ll}
f'(t) & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h) – f(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{ah(t+h t) – ah(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0} a \lim_{h \rightarrow 0}\frac{h(t+h) – h(t)}{h}\\
\ \ & = ah'(t).~~ \blacksquare
\end{array}\]
Ejercicio. Demuestre lo siguiente: Si $f(t)$ y $g(t)$ son funciones
vectoriales, entonces $(f+g)'(t)=f'(t)+g'(t)$
Solución
\[\begin{array}{ll}
(f+g)'(t) & = \displaystyle\lim_{h \rightarrow 0}\frac{f+g(t+h) – [f+g(t)]}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)+g(t+h) – f(t)-g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h) – f(t)}{h} + \frac{g(t+h) – g(t)}{h}\\
\ \ & = f'(t)+g'(t).~~ \blacksquare
\end{array}\]
Ejercicio. Pruebe lo siguiente: $(f\cdot g)'(t)=f(t)\cdot g'(t)+f'(t)\cdot g(t)$
Solución.
\[\begin{array}{ll}
(f\cdot g(t))’& = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\cdot g(t+h) – f(t)\cdot g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\cdot[g(t+h) – g(t)] +[f(t+h)-f(t)]\cdot g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\cdot[g(t+h) – g(t)]}{h} + \frac{[f(t+h) – f(t)]\cdot g(t)}{h}\\
\ \ & = f(t)\cdot g'(t)+f'(t)\cdot g(t).~ \blacksquare
\end{array}\]
$\fbox{$(f \times g)'(t)=f(t)\times g'(t)+f'(t)\times g(t)$}$
Solución.
\[\begin{array}{ll}
(f\times g(t))’& = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\times g(t+h) – f(t)\times g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\times [g(t+h) – g(t)] +[f(t+h)-f(t)]\times g(t)}{h}\\
\ \ & = \displaystyle\lim_{h \rightarrow 0}\frac{f(t+h)\times [g(t+h) – g(t)]}{h} + \frac{[f(t+h) – f(t)]\times g(t)}{h}\\
\ \ & = f(t)\times g'(t)+f'(t)\times g(t).~~ \blacksquare
\end{array}\]
Ejemplo. Dadas las funciones vectoriales
\begin{align*}
r(t)&=(6t+8)i+(4t^{2}+2t-3)j+5tk\\
u(t&)=(t^{2}-3)i+(2t+4)j+(t^{3}-3t)k
\end{align*}
calcule cada una de las siguientes derivadas usando las propiedades de la derivada de funciones vectoriales.
$$\displaystyle{\frac{d}{dt}[r(t)\cdot u(t)]}$$
$$\displaystyle{\frac{d}{dt}[u(t)\times u'(t)]}$$
En este caso tenemos que $r'(t)=6i+(8t+2)j+5k$ y $u'(t)=2ti+2j+(3t^{2}-3)k$. Por tanto
\begin{align*} \frac{d}{dt}[r(t)\cdot u(t)]&=r'(t)\cdot u(t)+r(t)\cdot u'(t) \\ &=(6i+(8t+2)j+5k)\cdot((t^{2}-3)i+(2t+4)j+(t^{3}-3t)k) \\ &+((6t+8)i+(4t^{2}+2t-3)j+5tk)\cdot(2ti+2j+(3t^{2}-3)k) \\ &=6(t^{2}-3)+(8t+2)(2t+4)+5(t^{3}-3t) \\ &+2t(6t+8)+2(4t^{2}+2t-3)+5t(3t^{2}-3) \\ &=20t^{3}+42t^{2}+26t-16. \end{align*}
Primero, necesitamos adaptar la propiedad correspondiente para este problema:
$$\frac{d}{dt}[u(t)\times u'(t)]=u'(t)\times u'(t)+u(t)\times u^{\prime\prime}(t)$$
Recuerda que el producto cruz de cualquier vector consigo mismo es cero. Además, $u^{\prime\prime}(t)$ representa la segunda derivada de $u(t)$:
$$u^{\prime\prime}(t)=\frac{d}{dt}[u'(t)]=\frac{d}{t}[2ti+2j+(3t^{2}-3)k]=2i+6tk$$
Por lo tanto
\begin{align*} \frac{d}{dt}[u(t)\times u'(t)]&=0+((t^{2}-3)i+(2t+4)j+(t^{3}-3t)k)\times (2i+6tk) \\ &=\left|\begin{matrix}i&j&k\\t^{2}-3&2t+4&t^{3}-3t\\2&0&6t\end{matrix}\right| \\ &=6t(2t+4)i-(6t(t^{2}-3)-2(t^{3}-3t))j-2(2t+4)k \\ &=(12t^{2}+24t)i+(12t-4t^{3})j-(4t+8)k.~ \blacksquare \end{align*}

Integrales de funciones con valores vectoriales

Introdujimos antiderivadas de funciones con valores reales en Antiderivadas e integrales definidas de funciones de valor real. Cada uno de estos conceptos se puede extender a funciones con valores vectoriales. Además, así como podemos calcular la derivada de un valor vectorial diferenciando las funciones componentes por separado, podemos calcular la antiderivada de la misma manera. Además, el Teorema Fundamental del Cálculo se aplica también a las funciones vectoriales. La antiderivada de una función vectorial aparece en las aplicaciones. Por ejemplo, si una función con valores vectoriales representa la velocidad de un objeto en el tiempo t, entonces su antiderivada representa la posición. O, si la función representa la aceleración del objeto en un momento dado, entonces la antiderivada representa su velocidad.
Sean $f_{1}(t),…,f_{n}(t)$ funciones de variable real sobre un intervalo $[a,b]$.
La integral indefinida de una función vectorial $r(t)=(f_{1}(t), \ldots,f_{n}(t))$ es
$$\boxed{\int~r(t)~dt=\int[(f_{1}(t), \ldots,f_{n}(t))]=\left[\int~f_{1}(t)~dt,~\int~f_{2}(t)~dt,…,\int~f_{n}(t)~dt\right]}$$
La integral definida de una función vectorial es
$$\boxed{\int_{a}^{b}~r(t)~dt=\int_{a}^{b}[(f_{1}(t), \ldots,f_{n}(t))]=\left[\int_{a}^{b}~f_{1}(t)~dt,~\int_{a}^{b}~f_{2}(t)~dt,…,\int_{a}^{b}~f_{n}(t)~dt\right]}$$
La integral existe siempre que cada una de las integrales $\displaystyle\int_{a}^{b}f_{i}(t)~dt$ con $i=1,\ldots,n$ existe. En particular, si $f_{i}$ es continua sobre $[a,b]$ entonces $\displaystyle\int_{a}^{b}f_{i}(t)~dt$ existe.
Dado que la integral indefinida de una función con valores vectoriales implica integrales indefinidas de las funciones componentes, cada una de estas integrales de componentes contienen una constante de integración. Todas pueden ser diferentes. Por ejemplo en el caso, en dos dimensiones, podemos tener
$$\int~r_{1}(t)~dt=F(t)+C_{1}~~y~~\int~r_{3}(t)~dt=G(t)+C_{2}$$
donde F y G son antiderivadas de $r_{1}(t)$ y $r_{2}(t)$, respectivamente. Entonces
\begin{align*} \int[r_{1}(t)+r_{2}(t)]~dt & =\left[\int~r_{1}(t)~dt\right]+\left[\int~r_{2}(t)~dt\right] \\ & =(F(t)+C_{1})+(G(t)+C_{2}) \\ & =F(t)+G(t)+C_{1}+C_{2} \\ & =F(t)+G(t)+C \end{align*}
donde $C=C_{1}i+C_{2}j$. Por lo tanto, la constante de integración se convierte en un vector constante.
Ejemplo. Calcula cada una de las siguientes integrales:
\begin{align*}
(a)&~\displaystyle{\int~[(3t^{2}+2t)i+(3t-6)j+(6t^{3}+5t^{2}-4)k]~dt}\\
(b)&~\displaystyle{\int~[(t,t^{2},t^{3})\times(t^{3},t^{2},t)]~dt}\\
(c)&~\displaystyle{\int_{0}^{\frac{\pi}{3}}~[\sin(2t)i+\tan(t)j+e^{-2t}k]~dt}
\end{align*}
(a) En este caso usamos la primera parte de la definición de la integral de una curva espacial:
\begin{align*} \int~[(3t^{2}+2t)i+(3t-6)j+(6t^{3}+5t^{2}-4)k]~dt&=\left[\int~(3t^{2}+2t)~dt\right]i+\left[\int~(3t-6)~dt\right]j \\ &+\left[\int~(6t^{3}+5t^{2}-4)~dt\right]k\\ &=\left(t^{3}+t^{2}\right)i+\left(\frac{3}{2}t^{2}-6t\right)j+\left(\frac{3}{2}t^{4}+\frac{5}{3}t^{3}-4t\right)k+C \end{align*}
(b) En este caso primero calcula $(t,t^{2},t^{3})\times (t^{3},t^{2},t)$
\begin{align*} (t,t^{2},t^{3})\times (t^{3},t^{2},t) & =\left|\begin{matrix}i&j&k\\t&t^{2}&t^{3}\\t^{3}&t^{2}&t\end{matrix}\right| \\ &=\left(t^{2}(t)-t^{3}(t^{2})\right)i-\left(t^{2}-t^{3}(t^{3})\right)j+\left(t(t^{2})-t^{2}(t^{3})\right)k \\ & =\left(t^{3}-t^{5}\right)i+\left(t^{6}-t^{2}\right)j+\left(t^{3}-t^{5}\right)k \end{align*}
A continuación, sustituya esto de nuevo en la integral e integre:
\begin{align*} \int~[(t,t^{2},t^{3})\times(t^{3},t^{2},t)]~dt&=\int~\left(t^{3}-t^{5}\right)i+\left(t^{6}-t^{2}\right)j+\left(t^{3}-t^{5}\right)k~dt \\ &=\left(\frac{t^{4}}{4}-\frac{t^{6}}{6}\right)i+\left(\frac{t^{7}}{7}-\frac{t^{3}}{3}\right)j+\left(\frac{t^{4}}{4}-\frac{t^{6}}{6}\right)k+C \end{align*}
(c) En este caso utilice la definición de la integral de una curva espacial:
\begin{align*} \int_{0}^{\frac{\pi}{3}}~[\sin(2t)i+\tan(t)j+e^{-2t}k]~dt&=\left[\int_{0}^{\frac{\pi}{3}}~\sin(2t)~dt\right]i+\left[\int_{0}^{\frac{\pi}{3}}~\tan(t)~dt\right]j+\left[\int_{0}^{\frac{\pi}{3}}~e^{-2t}~dt\right]k \\ &=\left(-\frac{1}{2}\cos(2t)\right)\Big{|}{0}^{\frac{\pi}{3}}i-\left(\ln(\cos(t))\right)\Big{|}{0}^{\frac{\pi}{3}}j-\left(\frac{1}{2}e^{-2t}\right)\Big{|}_{0}^{\frac{\pi}{3}}k \\
&=\left(-\frac{1}{2}\cos\frac{2\pi}{3}+\frac{1}{2}\cos(0)\right)i-(\ln\left(\cos\frac{\pi}{3}\right)-\ln(\cos(0)))j \\
&-\left(\frac{1}{2}e^{-\frac{2pi}{3}}-\frac{1}{2}e^{-2(0)}\right)k\\
&=\left(\frac{1}{4}+\frac{1}{2}\right)i-(-\ln(2))j-\left(\frac{1}{2}e^{-\frac{2\pi}{3}}-\frac{1}{2}\right)k\\
&=\frac{3}{4}i+(\ln(2))j+\left(\frac{1}{2}-\frac{1}{2}e^{-\frac{2\pi}{3}}\right)k.~~ \blacksquare
\end{align*}
Teorema.
Si $f=(f_{1}, \ldots,
f_{n})$ es continua sobre un intervalo $I$ y $a\,\epsilon\,I$
entonces:
$$\frac{d\displaystyle\int_{a}^{t}f}{dt}=f(t) \quad \forall \quad t\,\epsilon\,I$$
Demostración. En este caso se obtiene por la aplicación del primer teorema fundamental
del cálculo a cada una de las funciones componentes
\begin{align*} \int_{a}^{t}f(t)~dt&=\left(\int_{a}^{t}f_{1}(t)~dt, \ldots,\int_{a}^{t}f_{n}(t)~dt\right) \\ &=\left(\frac{d}{dt}\int_{a}^{t}f_{1}(t)~dt,ldots,\frac{d}{dt}\int_{a}^{t}f_{n}(t)~dt\right) \\ &=(f_{1}(t), \ldots , f_{n}(t)) \\ &= f(t).~~ \blacksquare \end{align*}
Teorema. Si $f(t)=(f_{1}(t), \ldots,
f_{n}(t))$ tiene derivada continua sobre un intervalo $I$, entonces
$\forall~~ a,b\,\in I,~~\displaystyle\int_{a}^{b}f'(t)=f(b)-f(a)$
Demostración.
\begin{align*} \int_{a}^{b}f’& =\int_{a}^{b}(f’_{1}, \ldots,f’_{n}) \\
& =\left( \displaystyle\int_{a}^{t}f’_{1}, \ldots, \displaystyle\int{a}^{t}f’_{n}\right) \\ & = \left( f_{1}(b)-f_{1}(a), \ldots,f_{n}(b)-f_{n}(a)\right)\\
& = f(b)-f(a).~~ \blacksquare
\end{align*}
Ejemplo.
Si $f(t)=(f_{1}(t),f_{2}(t),…,f_{n}(t))$ es integrable en $[a,b]$, para todo vector $C=(c_{1},c_{2},…,c_{n})$ entonces el producto escalar $C\cdot F$ es integrable en $[a,b]$ y $$C\cdot \int_{a}^{b} f(t)dt= \int_{a}^{b}C\cdot f(t)dt$$
En efecto tenemos que
\begin{align*} C\cdot \int_{a}^{b} f(t)dt&=(c_{1},c_{2},…,c_{n})\cdot\left(\int_{a}^{b} f_{1}(t)dt,\int_{a}^{b} f_{2}(t)dt,…,\int_{a}^{b} f_{n}(t)dt\right) \\ &=\left(c_{1}\cdot\int_{a}^{b} f_{1}(t)dt+c_{2}\cdot\int_{a}^{b} f_{2}(t)dt+…+c_{n}\cdot\int_{a}^{b} f_{n}(t)dt\right) \\ &=\left(\int_{a}^{b}c_{1}\cdot f_{1}(t)dt+,\int_{a}^{b} c_{2}\cdot f_{2}(t)dt+…+\int_{a}^{b}c_{n}\cdot f_{n}(t)dt\right) \\ &=\int_{a}^{b}C\cdot f(t) dt.~~ \blacksquare \end{align*}

Más adelante

Tarea Moral

Enlaces

Introducción

Ahora echemos un vistazo al límite de una función con valores vectoriales. Esto es importante de entender para estudiar el cálculo de funciones vectoriales.

Definición. Sea $f:\mathbb{R}\rightarrow \mathbb{R}^{n}$ una función vectorial definida para todos los valores de
$t$ en alguna vecindad de un punto $t_0$, excepto quiza en $t_0$.
Entonces se dice que el límite de la función f cuando $t$ se acerca a $t_0$ es $L\in\mathbb{R}^{n}$ y se expresa como
\[
\lim_{t\rightarrow t_0} f(t)=L
\]
si y solo si $\forall$ $\epsilon>0$ $\exists ~\delta~>~0$ tal que $|f(t)-L|~<~\epsilon$, siempre que $|t-t_0|<\delta$

Teorema. Si $f:I\subset\mathbb{R}\rightarrow\mathbb{R}^n$ es una función vectorial, entonces
\[
\lim_{t\rightarrow t_0}f(t)=L=(l_1,\cdots,l_n)\in \mathbb{R}^n\ \ \
\Leftrightarrow\ \ \ \lim_{t\rightarrow t_0}x_i(t)=l_i~~\forall~i=1,…,n
\]
Donde $f(t)=(x_1(t),\cdots,x_n(t))$

Demostración. Si
\[
\lim_{t\rightarrow t_0}f(t)=L
\]
entonces $\forall$ $\epsilon>0$ $\exists$ $\delta>0$ tal que si
$0<|t-t_0|<\delta$, entonces $|f(t)-L|<\epsilon$. Pero como \[ |f(t)-L|=|x_1(t)-l_1,\cdots,x_n(t)-l_n|= \left(\sum_{i=1}^n(x_i(t)-l_i)^2\right)^{\frac{1}{2}}<\epsilon \] se tiene que \[ |x_i(t)-l_i|\leq\left(\sum_{i=1}^n(x_i(t)-l_i)^2\right)^{\frac{1}{2}}<\epsilon \] Por lo tanto dado $\epsilon>0$ existe $\delta>0$ tal que
$0<|t-t_0|<\delta\Rightarrow|x_i(t)-l_i|<\epsilon$ por lo tanto
\[
\lim_{t\rightarrow t_0}x_i(t)=l_i
\]
Reciprocamente supongamos ahora que
\[
\lim_{t\rightarrow t_0}x_i(t)=l_i\ \ \ \ \ i=1,\cdots,n.
\]
Esto quiere decir que $\forall$ $\epsilon_i>0$ $\exists$ $\delta_i>0$ tal que $0<|t-t_0|<\delta_i\Rightarrow|x_i(t)-l_i|<\epsilon_i$.

Sea $\epsilon>0$ y sea $\displaystyle{\epsilon_i=\frac{\epsilon}{\sqrt{n}}}$ tomamos $\delta=\textbf{min}(\delta_1,\cdots,\delta_n)$.

Para esta $\delta$ se tiene que si $0<|t-t_0|<\delta\Rightarrow|x_i(t)-l_i|<\frac{\epsilon}{\sqrt{n}}$ $\forall$ $i=1,\cdots,n$, entonces
\[
|f(t)-L|=\left(\sum_{i=1}^n(x_i(t)-l_i)^2\right)^\frac{1}{2}<
\left(\sum_{i=1}^n\left(\frac{\epsilon}{\sqrt{n}}\right)^2\right)^\frac{1}{2}=\epsilon
\]
Por lo tanto
\[
\lim_{t\rightarrow t_0}f(t)=L~~ \blacksquare
\]

Ejemplo. Se sabe que
\[
\lim_{t\rightarrow 2} (t,t)=(2,2)
\]
Dado $\epsilon>0$, determine $\delta>0$ que verifique la
validez del límite.

Tenemos que
\[
\lim_{t\rightarrow 2}(t,t)=\left(\lim_{t\rightarrow 2}t,
\lim_{t\rightarrow 2}t\right)=(2,2)
\]

$\therefore$ Según la definición
$$|(t,t)-(2,2)|=\sqrt{(t-2)^2+(t-2)^2}=\sqrt{2(t-2)^2}=\sqrt{2}|t-2|$$
$$\therefore \quad si\quad \sqrt{2}|t-2|<\epsilon$$ podemos definir a $\displaystyle{\delta=\frac{\epsilon}{\sqrt{2}}}$.$~~ \blacksquare$

Ejemplo. Se sabe que
\[
\lim_{t\rightarrow 2} (t,t^{3})=(2,8)
\]
Dado $\epsilon>0$, determine $\delta>0$ que verifique la
validez del límite.

Tenemos que
\[
\lim_{t\rightarrow 2}(t,t^{3})=\left(\lim_{t\rightarrow 2}t,
\lim_{t\rightarrow 2}t^{3}\right)=(2,8)
\]
Ahora bien para $\displaystyle{\delta_{1}=\frac{\epsilon}{\sqrt{2}}}$ se tiene
$$0<|t-2|<\delta_{1}~\Rightarrow~|t-2|<\frac{\epsilon}{\sqrt{2}}$$

y para $\displaystyle{\delta_{2}=\frac{\epsilon}{\sqrt{2}}}$ se tiene
$$0<|t-2|<\delta_{2}~\Rightarrow~|t^{3}-8|<\frac{\epsilon}{\sqrt{2}}$$
Por lo tanto si consideramos $\delta=min{\delta_{1},\delta_{2}}$ se tiene
$$|(t,t^{3})-(2,8)|=\sqrt{(t-2)^2+(t^{3}-8)^2}<\sqrt{\left(\frac{\epsilon}{\sqrt{2}}\right)^2+\left(\frac{\epsilon}{\sqrt{2}}\right)^2}=\sqrt{2\frac{\epsilon^{2}}{2}}=\epsilon$$
$$\therefore \lim_{t\rightarrow 2} (t,t^{3})=(2,8).~~ \blacksquare$$

Continuidad de Funciones Vectoriales

Ahora que sabemos cómo calcular el límite de una función vectorial, podemos definir la continuidad en un punto para tal función.

Definición. Sea $f:\mathbb{R}\rightarrow\mathbb{R}^n$ una función vectorial. Se dice que $f$ es continua en $t_0$ si y solo si se cumple que
\[
\lim_{t\rightarrow t_0}f(t)=f(t_0)
\]

Teorema. La función vectorial
$f(t)=(x_{1}(t),x_{2}(t),…,x_{n}(t))$ es continua en $t_0$ si y
solo si $x_{1},x_{2},…,x_{n}$ son continuas en $t_0$.

Demostración. Como $f(t)$ es continua en $t=t_{0}$, tenemos que se cumple $$\lim_{t\rightarrow t_{0}}f(t)=f(t_{0})$$
Por otro lado se tiene que $$\lim_{t\rightarrow t_{0}}f(t)=\lim_{t\rightarrow t_{0}}\left(x_{1}(t),x_{2}(t),…,x_{n}(t)\right)=\left(\lim_{t\rightarrow t_{0}}x_{1}(t),\lim_{t\rightarrow t_{0}}x_{2}(t),…,\lim_{t\rightarrow t_{0}}x_{n}(t)\right)$$
y como $f(t_{0})=(x_{1}(t_{0}),x_{2}(t_{0}),…,x_{n}(t_{0}))$ entonces
$$\left(\lim_{t\rightarrow t_{0}}x_{1}(t),\lim_{t\rightarrow t_{0}}x_{2}(t),…,\lim_{t\rightarrow t_{0}}x_{n}(t)\right)=(x_{1}(t_{0}),x_{2}(t_{0}),…,x_{n}(t_{0}))$$
$$\therefore \quad \lim_{t\rightarrow t_{0}}x_{1}(t)=x_{1}(t_{0})\quad , \quad \lim_{t\rightarrow t_{0}}x_{2}(t)=x_{2}(t_{0}),…,\lim_{t\rightarrow t_{0}}x_{n}(t)=x_{n}(t_{0})$$
$\therefore$ $x_{1}(t),x_{2}(t),…x_{n}(t)$ son continuas en $t=t_{0}$.$~~ \blacksquare$

Ejemplo. Definir la función
\[
f(t)=\frac{\sin t}{t}\hat{i}+\cos (t) \hat{j}
\]
en $t=0$ de manera que $f(t)$ sea continua en $t=0$.

Tenemos que
\[
\lim_{t\rightarrow 0}f(t)=
\lim_{t\rightarrow 0}\frac{\sin t}{t}\hat{i}+\cos t \hat{j}=
\hat{i}+\hat{j}
\]
Por lo tanto si definimos $f(0)=\hat{i}+\hat{j}$, entonces
\[
\lim_{t\rightarrow t_0} f(t)=f(t_0).~~ \blacksquare
\]

Teorema. Si f es continua en $A\subset \mathbb{R}$ entonces para toda sucesión $x_{k}$ en A tal que $x_{k}\rightarrow x_{0}$ se tiene que $f(x_{k})\rightarrow f(x_{0})$

Demostración. $\left(\textcolor{red}{\Rightarrow}\right)$ Supongamos que $x_{k}\rightarrow x$ para mostar que $f(x_{k})\rightarrow f(x)$ sea $\epsilon>0$ como f es continua en $x_{0}\in A$ se tiene que $$0<|x-x_{0}|<\delta\Rightarrow |f(x)-f(x_{0})|<\epsilon$$ elegimos entonces $k>N$ tal que

$$|x_{k}-x_{0}|<\delta\Rightarrow |f(x_{k})-f(x_{0})|<\epsilon$$

$\left(\textcolor{red}{\Leftarrow}\right)$ Supongamos que para cada $x_{k}\in A$ tal que $x_{k}\rightarrow x$ se tiene que $|f(x_{k})-f(x)|<\epsilon$ y queremos demostrar que f es continua en $x_{0}$. Si $x_{k}\rightarrow x_{0}$ entonces $|x_{k}-x_{0}|<\epsilon$ si $k>N_{0}$ tomemos $\delta=\epsilon_{1}$ y tenemos que $$|x_{k}-x_{0}|<\epsilon_{1}\Rightarrow|x_{k}-x_{0}|<\delta\Rightarrow|f(x_{k})-f(x_{0})|<\epsilon~~ \blacksquare$$

Más adelante

Ya que se definieron las funciones vectoriales y se abordó el tema límites y continuidad en estas, a continuación veremos el cálculo subyacente a este tipo de funciones como lo son la derivabilidad y la integrabilidad.

Tarea Moral

1.- Determina el siguiente límite:

\[
\lim_{ x \rightarrow 1}(\dfrac{x^2-1}{x-1}, \sqrt(x+8), \frac{sen\pi x}{ln x})
\]

2.- Analiza la continuidad de la siguiente función

\[f \left( x\right) =\begin{cases}\left( x,\dfrac{senx}{x}\right), \text{si} x \neq 0 \\ \left( 0,1\right) \text{si} x= 0 \end{cases}\]

3.- Si \[
\lim_{ x \rightarrow a} f(x) = b
\] pruebe que \[
\lim_{ x \rightarrow a} | f(x)| =|b|
\]

5.- Si \[
\lim_{ x \rightarrow a} f(x) = b
\] pruebe que \[
\lim_{ x \rightarrow a} \dfrac {f(x) }{ | f(x)|}=\dfrac{b}{|b|}
\]

Enlaces