Definición: Área

La noción intuitiva de área de una región en el plano es el número
de unidades cuadradas contenidas en la región.

Al definir área aceptaremos que el área $A(S)$ de un conjunto
debe ser un número no negativo con las propiedades siguientes:

1.-Si S es un cuadrado de lado K entonces $A(S)=K^2$

2.-El área del todo es la suma de las áreas de sus partes.
Más precisamente si $S$ consiste de los conjuntos que no se
traslapan $S_{1}$,…,$S_{n}$ de áreas $A(S_{1})$,…,$A(S_{n})$
respectivamente, entonces el área de $S$ es $$A(S)=A(S_{1})+\ldots+A(S_{n}).$$

Los cuadrados congruentes proporcionan la manera más fácil de
cubrir el plano sin espacios vacíos o traslapes. Usaremos la rejilla asociada al sistema coordenado proporcionada por
las rectas $x=0,\pm1,\pm2,…$ e $y=0,\pm1,\pm2,…$ la cual
divide al plano en cuadrados de lado 1.

Denotamos $\displaystyle {A_0^{+}(S)}$ el número de cuadrados que
tienen puntos en común con $S$ y $\displaystyle {A_0^{-}(S)}$ el
número de aquellos que están completamente contenidos en $S$

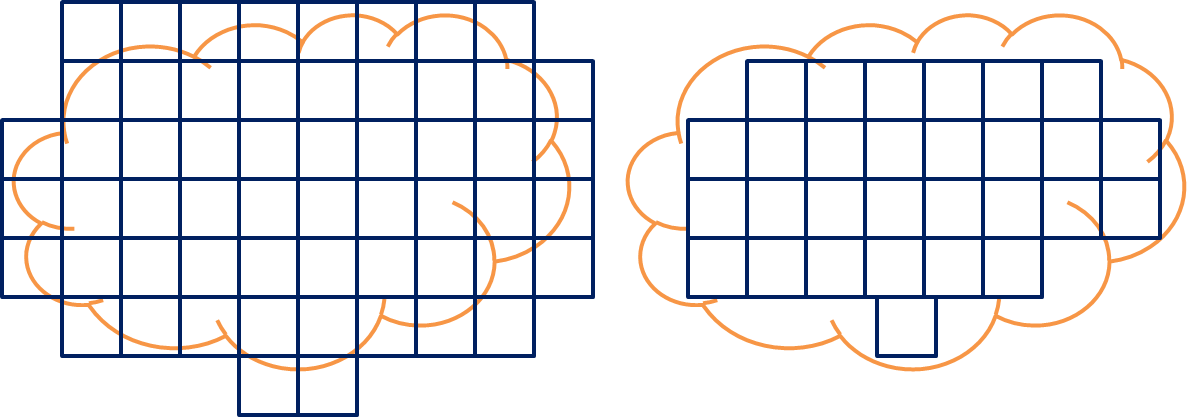
Dividamos ahora cada cuadrado en 4 partes iguales de lado
$\displaystyle{\frac{1}{2}}$ y área $\displaystyle{\frac{1}{4}}$.
Sea $\displaystyle A_1^{+}(S)$ la cuarta parte del número de
aquellos subcuadrados que tienen puntos en común con $S$ y
$\displaystyle A_1^{-}(S)$ la cuarta parte de aquellos completamente
contenidos en $S$.

Se tiene que $\displaystyle{A_0^{-}(S)\leq\displaystyle A_1^{-}(S)}$ y de modo semejante
$\displaystyle{A_0^{+}(S)\geq A_1^{+}(S)}$, al continuar dividiendo cada cuadrado de lado $\displaystyle{\frac{1}{2}}$ en 4 cuadrados de lado $\frac{1}{4}$. Un dieciseisavo de esos cuadrados que tienen puntos en común con $S$ y un dieciseisavo de esos cuadrados que estan completamente contenidos en $S$, se denotaran por
$\displaystyle{A_2^{+}(S)}$ y $\displaystyle{A_2^{-}(S)}$. \Procediendo de esta forma se asocian los valores $\displaystyle{A_n^{+}(S)}$ y $\displaystyle{A_n^{-}(S)}$ con una división en cuadrados de lado $2^{n}$. Es evidente que los valores $\displaystyle{ A_n^{+}(S)}$ forman una sucesión monótona decreciente y acotada que converge hacia un valor $\displaystyle{A^{+}(S)}$, mientras que los valores $\displaystyle{A_n^{-}(S)}$ crecen monótonamente y convergen hacia un valor $\displaystyle{A^{-}(S)}$.
El valor $\displaystyle{A^{-}(S)}$ representa el área interior, lo mejor que
puede aproximarse el área de $S$ desde abajo por medio de cuadrados
congruentes contenidos en $S$, el área exterior $\displaystyle{A^{+}(S)}$
representa la mejor cota superior obtenible cubriendo a $S$ por
medio de cuadrados congruentes. Podemos denotar $\displaystyle{ A_n^{-}=\sum_{ik}
2^{-2n}}$ con $R_{ik}\subset S$, $\displaystyle{A_n^{+}=\sum_{ik}2^{-2n}}$ con $R_{ik}\cap S\neq\emptyset$ a partir de la definición resulta $0\leq\displaystyle {A_n^{-}}\leq\displaystyle{A_n^{+}}$.\ Las sumas $\displaystyle {A_n^{-}}$ forman una sucesión no decreciente con la cota superior $\displaystyle{A_1^{+}}$ así, convergen hacia un limite $A^{-}=\displaystyle{\lim_{n\rightarrow\infty} A_n^{-}}$.
De manera semejante Las sumas $\displaystyle{A_n^{+}}$ forman una sucesión no
creciente con la cota superior $\displaystyle{A_1^{-}}$ así, convergen hacia un limite
$A^{+}=\displaystyle{\lim_{n\rightarrow\infty}} \displaystyle {A_n^{+}}$.
Si ambos valores concuerdan se dice que $S$ es mesurable según
Jordan y el valor común $\displaystyle{A^{-}(S)=A^{+}(S)}$ se llama contenido, o
medida de Jordan de $S$.

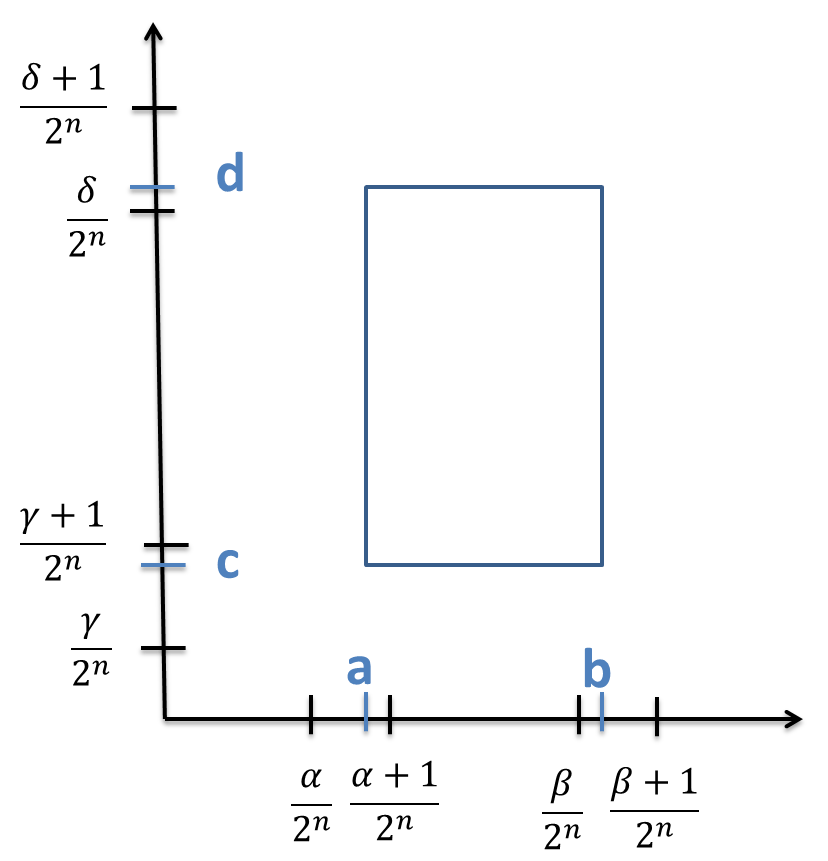
Más generalmente, cualquier rectángulo $S$ con lados paralelos a
los ejes coordenados, $S: a\leq x\leq b,~~~c\leq y\leq d$.

Dado un entero positivo n, se pueden encontrar enteros
$\alpha,~\beta,~\gamma,~\delta$ tales que

$\alpha <a\cdot2^{n}\leq\alpha+1,~~~\gamma<c\cdot2^{n}\leq\gamma+1$

$\beta\leq b\cdot2^{n}<\beta+1~~~~\delta\leq d\cdot2^{n}<\delta+1$

por lo tanto
$\displaystyle{\frac{\alpha}{2^{n}}<a\leq\frac{ \alpha+1}{2^{n}}}$
$\displaystyle{\frac{\gamma}{2^{n}}<c\leq\frac{ \gamma+1}{2^{n}}}$

$\displaystyle{\frac{\beta}{2^{n}}\leq b<\frac{\beta+1}{2^{n}}}$

$\displaystyle{\frac{\delta}{2^{n}}\leq d<\frac{\delta+1}{2^{n}}}$

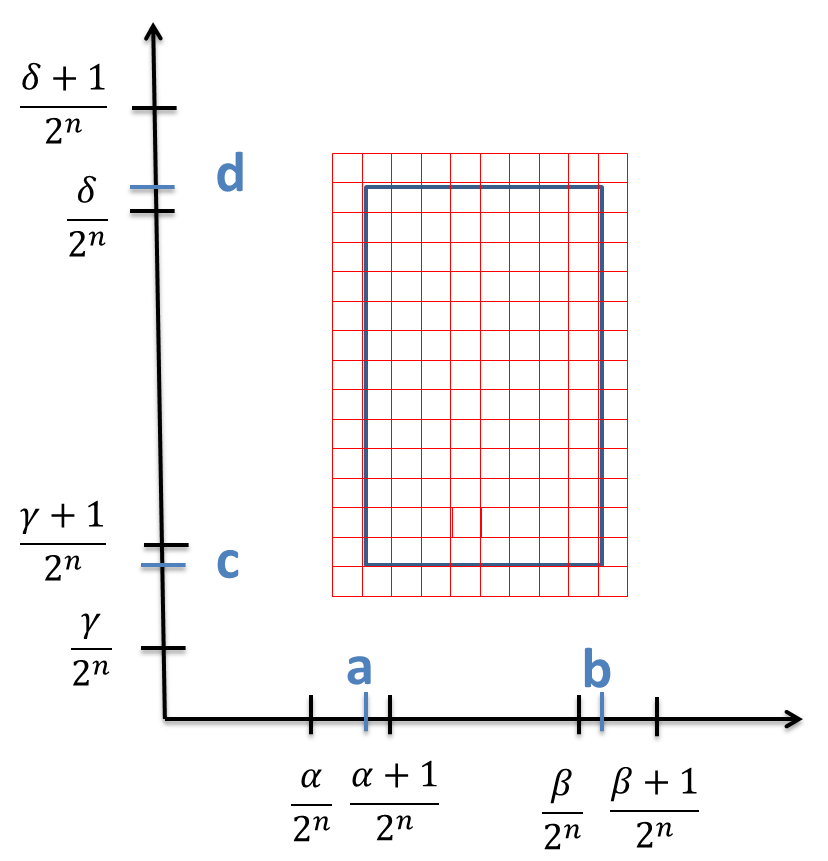
Usando una rejilla adecuada de longitud $2^{n}$ tenemos que

$\displaystyle{\frac{\beta}{2^{n}}-\frac{\alpha+1}{2^{n}}+\frac{2}{2^{n}}\leq b-a+\frac{2}{2^{n}}}$

$ \displaystyle{ \frac{\beta+1}{2^{n}}-\frac{\alpha}{2^{n}}-\frac{2}{2^{n}}\geq b-a-\frac{2}{2^{n}}}$

$ \displaystyle{ \frac{\delta}{2^{n}}-\frac{\gamma+1}{2^{n}}+\frac{2}{2^{n}}\leq d-c+\frac{2}{2^{n}}}$

$ \displaystyle{ \frac{\delta+1}{2^{n}}-\frac{\gamma}{2^{n}}-\frac{2}{2^{n}}\geq d-c-\frac{2}{2^{n}}}$

Por lo tanto
$$A_{n}^{+}=\left(\frac{\beta}{2^{n}}-\frac{\alpha+1}{2^{n}}+\frac{2}{2^{n}}\right)\left(\frac{\delta}{2^{n}}-\frac{\gamma+1}{2^{n}}+\frac{2}{2^{n}}\right)$$
$$A_{n}^{-}=\left(\frac{\beta+1}{2^{n}}-\frac{\alpha}{2^{n}}-\frac{2}{2^{n}}\right)\left(\frac{\delta+1}{2^{n}}-\frac{\gamma}{2^{n}}-\frac{2}{2^{n}}\right)$$

De la desigualdad
$$A_{n}^{-}\leq A\leq A_{n}^{+}$$
tenemos que
$$\left(\frac{\beta+1}{2^{n}}-\frac{\alpha}{2^{n}}-\frac{2}{2^{n}}\right)\left(\frac{\delta+1}{2^{n}}-\frac{\gamma}{2^{n}}-\frac{2}{2^{n}}\right)\leq A\leq\left(\frac{\beta}{2^{n}}-\frac{\alpha+1}{2^{n}}+\frac{2}{2^{n}}\right)\left(\frac{\delta}{2^{n}}-\frac{\gamma+1}{2^{n}}+\frac{2}{2^{n}}\right)$$
como
$$\left(b-a-\frac{2}{2^{n}}\right)\left(d-c-\frac{2}{2^{n}}\right)\leq\left(\frac{\beta+1}{2^{n}}-\frac{\alpha}{2^{n}}-\frac{2}{2^{n}}\right)\left(\frac{\delta+1}{2^{n}}-\frac{\gamma}{2^{n}}-\frac{2}{2^{n}}\right)$$
$$\left(\frac{\beta}{2^{n}}-\frac{\alpha+1}{2^{n}}+\frac{2}{2^{n}}\right)\left(\frac{\delta}{2^{n}}-\frac{\gamma+1}{2^{n}}+\frac{2}{2^{n}}\right)\leq\left(b-a+\frac{2}{2^{n}}\right)\left(d-c+\frac{2}{2^{n}}\right)$$
entonces
$$\left(b-a-\frac{2}{2^{n}}\right)\left(d-c-\frac{2}{2^{n}}\right)\leq A_{n}^{-}\leq A\leq A_{n}^{+}\leq \left(b-a+\frac{2}{2^{n}}\right)\left(d-c+\frac{2}{2^{n}}\right)$$
por lo tanto
$$\lim_{n\rightarrow\infty}\left(b-a-\frac{2}{2^{n}}\right)\left(d-c-\frac{2}{2^{n}}\right)\leq \lim_{n\rightarrow\infty}A_{n}^{-}=A=\lim_{n\rightarrow\infty}A_{n}^{+}\leq \lim_{n\rightarrow\infty}\left(b-a+\frac{2}{2^{n}}\right)\left(d-c+\frac{2}{2^{n}}\right)$$
$A=\displaystyle\lim_{n\rightarrow\infty} \displaystyle
A_n^{+}=\displaystyle \lim_{n\rightarrow\infty} \displaystyle
A_n^{-}=(b-a)(d-c)$.