MATERIAL EN REVISIÓN

Introducción

Esta es la primera entrada correspondiente al curso de análisis matemático II. Para esta primera parte del curso estudiaremos la integración de Lebesgue, una noción de integral muy poderosa y sobre la que se construye gran parte del análisis matemático moderno. Veremos una forma precisa de definir conceptos como longitud, área, volumen y sus análogos en más dimensiones: La medida de Lebesgue, sobre la cual construiremos este concepto de integración. Luego, estudiaremos las principales propiedades de la integral de Lebesgue, su relación con la integral de Riemann y una serie de teoremas muy útiles para calcular y estimar integrales: Los teoremas de convergencia y el teorema de Fubini.

Motivación

En tus cursos anteriores seguramente te has encontrado con el concepto de integral de Riemann. Ésta es una herramienta computacional muy poderosa que, a grosso modo, nos ayuda a encontrar el «área bajo la curva» en una dimensión y sus análogos en dimensiones más altas. Sin embargo, tiene una serie de limitaciones que hacen deseable un concepto de integración más general. A modo de motivación, recapitulamos algunas de ellas:

La clase de funciones integrables en el sentido de Riemann es limitada.

Como ejemplo, considera la función de Dirichlet ${\chi }_{\mathbb{Q}}:[0,1]\to \mathbb{R}$ definida como:

$${\chi }_{\mathbb{Q}}(x)=\{\begin{array}{ll}1& \text{si }x\in \mathbb{Q}\\ 0& \text{si }x\in \mathbb{R}\setminus \mathbb{Q}\end{array}$$

Observa que si $[a,b]\subseteq [0,1]$ con $a<b$ entonces $\underset{x\in [a,b]}{inf}f(x)=0$ y $\underset{x\in [a,b]}{sup}f(x)=1$, pues $[a,b]$ contiene números racionales e irracionales.

Recordemos que en el contexto de integrales de Riemann las sumas inferiores y superiores de la función $f$, sobre una partición $P=\{a=x_0<x_1<\cdots <x_n=b\}$ se definen como:
$$L(f,P,[a,b])=\sum _{j=1}^n(x_j-x_{j-1})\underset{[x_{j-1},x_j]}{inf}f$$ $$S(f,P,[a,b])=\sum _{j=1}^n(x_j-x_{j-1})\underset{[x_{j-1},x_j]}{sup}f$$

Y se dice que la función es Riemman integrable si $$L(f,[a,b]):=\underset{P}{sup}L(f,P,[a,b])$$ Y $$S(f,[a,b]):=\underset{P}{inf}S(f,P,[a,b])$$ Coinciden. La integral de Riemann se define como el valor común: $$L(f,[a,b])=S(f,[a,b]).$$
En nuestro ejemplo, es fácil ver que $L({\chi }_{\mathbb{Q}},P,[a,b])=0$, $S({\chi }_{\mathbb{Q}},P,[a,b])=1$ para cualquier partición $P$, de modo que $$L({\chi }_{\mathbb{Q}},[a,b])=0$$ Y $$S({\chi }_{\mathbb{Q}},[a,b])=1.$$ Por lo que la función NO es Riemann integrable. Sin embargo, es natural pensar que la integral debería ser 0 pues hay «muy pocos racionales en comparación con los irracionales en $[0,1]$». El siguiente ejemplo refuerza esta intuición.

La integral de Riemann no se comporta bien bajo operaciones de límite.

Si consideramos alguna numeración de los números racionales en $\mathbb{Q}\cap [0,1]=\{r_1,r_2,\dots \}$ y para cada $k\in {\mathbb{Z}}^{\mathbb{+}}$ definimos $f_k:[0,1]\to \mathbb{R}$ como:

$$f_k(x)=\{\begin{array}{ll}1& \text{si }x\in \{r_1,r_2,\dots ,r_k\}\\ 0& \text{en otro caso }\end{array}$$

Se verifica que $f_k$ es Riemann integrable y ${\int }_0^1{f}_k(x)\mathrm{d}x=0$, pues $f$ es acotada y vale 0 salvo en una cantidad finita de puntos.

Observa que si $x$ es irracional, $f_k(x)=0$ $\mathrm{\forall }k$; y si $x$ es racional, $x=r_N$ para algún $N$ de modo que $f_k(x)=1$ $\mathrm{\forall }n\ge N$. Esto nos dice que ${\chi }_{\mathbb{Q}}$ es el límite puntual de la sucesión de funciones $f_k$ pero ${\chi }_{\mathbb{Q}}$ no es Riemann integrable.

En el ejemplo anterior la sucesión $f_k$ se puede modificar para hacerla continua o incluso suave. Piensa por ejemplo en sustituir las discontinuidades de salto por crestas de funciones lineales a pedazos o pulsos suaves cuya anchura se va haciendo arbitrariamente pequeña. En general, esto nos dice que la clase de funciones Riemann integrables no es cerrada bajo toma de límites (puntuales), ni siquiera si las funciones son «bien portadas».

Con nociones más fuertes de convergencia, por ejemplo convergencia uniforme (una hipótesis muy «fuerte»), se tienen mejores resultados respecto a toma de límites. El siguiente es bien conocido:

Teorema. Sea $f_k:[a,b]\to \mathbb{R}$, $k\in \mathbb{N}$, una sucesión de funciones Riemann integrables que convergen uniformemente a $f:[a,b]\to \mathbb{R}$. Entonces $f$ es Riemann integrable y además $$\underset{k\to \mathrm{\infty }}{lim}{\int }_a^b{f}_k(x)\mathrm{d}x={\int }_a^{b}f(x)\mathrm{d}x.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

También en el contexto de toma de límites, otra pregunta relevante es ¿bajo qué condiciones la integral conmuta con un límite?, o al menos ¿se puede decir algo sobre la integral de un límite?. Estas son preguntas que surgen normalmente en áreas como ecuaciones diferenciales, análisis de Fourier o probabilidad, en la que muchos conceptos se definen precisamente como un límite (por ejemplo la derivada o las series de Fourier). El ejemplo anterior no es muy esperanzador pues puede que un límite puntual ni siquiera sea Riemann integrable. Bajo ciertas condiciones sí se puede decir algo, por ejemplo:

Teorema (de la convergencia acotada). Sea $f_k:[a,b]\to \mathbb{R}$ una sucesión de funciones Riemann integrables y acotadas tales que $\mathrm{\exists }M\in \mathbb{R}$ tal que $|f_k(x)|\le M$ para todo $k\in \mathbb{N}$ y $x\in [a,b]$. Si $f_k$ convergen puntualmente a $f$ y $f$ es Riemann integrable, entonces $$\underset{k\to \mathrm{\infty }}{lim}{\int }_a^b{f}_k(x)\mathrm{d}x={\int }_a^{b}f(x)\mathrm{d}x.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

¿Habrá alguna noción de integración que sea más laxa respecto a toma de límites?¿Se podrán mejorar los resultados enunciados?

La integral de Riemann no maneja adecuadamente funciones no acotadas o dominios no acotados.

Por definición, la integral de Riemann se define para funciones acotadas sobre intervalos cerrados finitos. Para funciones no acotadas o dominios no acotados la forma clásica de abordar estos problemas es con integrales impropias. Considera los siguientes ejemplos:

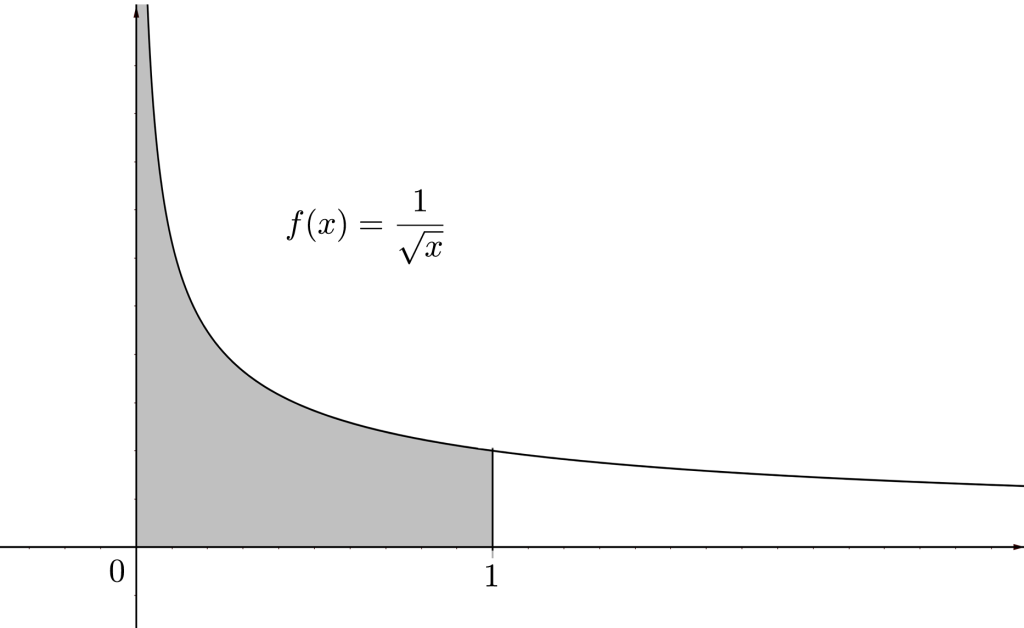
Ejemplo. La función $f(x)=\frac{1}{\sqrt{x}}$ no está acotada en $[0,1]$, sin embargo podemos hablar de área bajo la curva con la integral impropia:

$$\begin{array}{rl}\underset{a\downarrow 0}{lim}{\int }_a^{1}f(x)\mathrm{d}x& =\underset{a\downarrow 0}{lim}{\int }_a^1\frac{1}{\sqrt{x}}\mathrm{d}x\\ & =\underset{a\downarrow 0}{lim}[2x^{\frac{1}{2}}{]}_a^1\\ & =\underset{a\downarrow 0}{lim}[2-2\sqrt{a}]\\ & =2\end{array}$$

$\mathrm{△}$

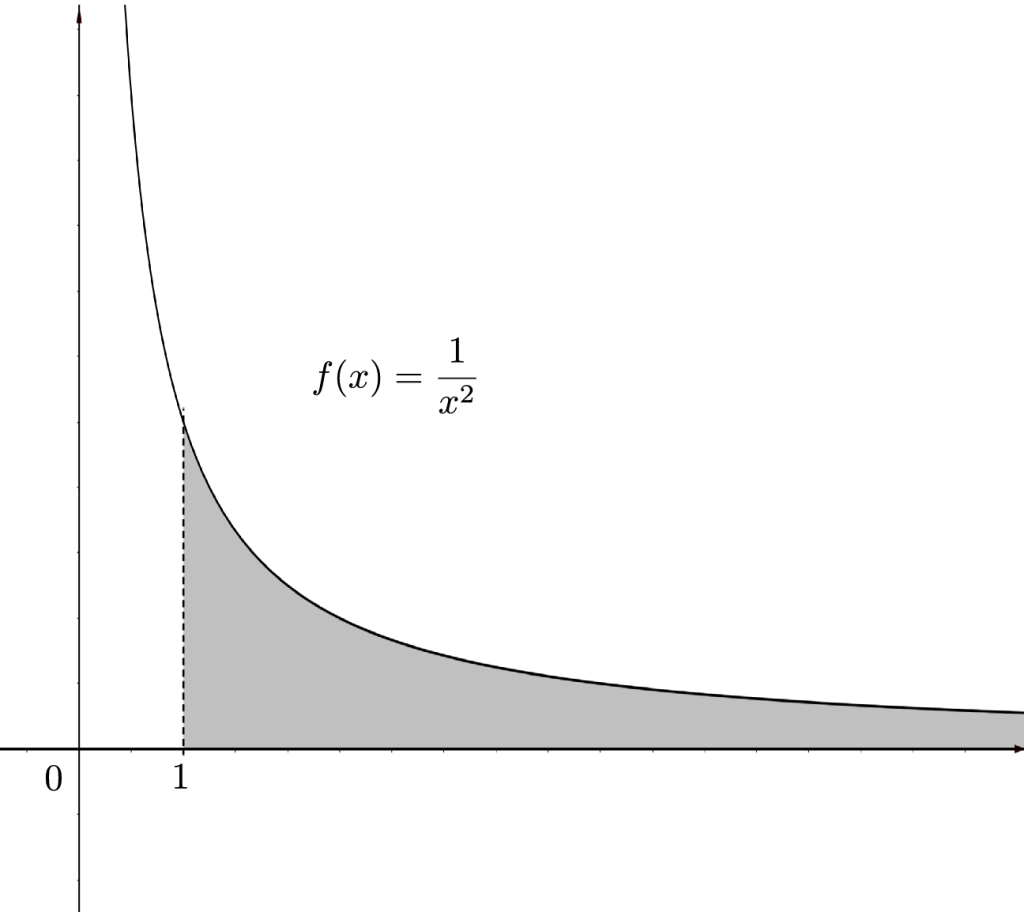
Ejemplo. Algo similar ocurre con $f(x)=\frac{1}{x^2}$ pero en el intervalo $[1,\mathrm{\infty })$:

$$\begin{array}{rl}\underset{N\to \mathrm{\infty }}{lim}{\int }_1^{N}f(x)\mathrm{d}x& =\underset{N\to \mathrm{\infty }}{lim}{\int }_1^N\frac{1}{x^2}\mathrm{d}x\\ & =\underset{N\to \mathrm{\infty }}{lim}{[-\frac{1}{x}]}_1^N\\ & =\underset{N\to \mathrm{\infty }}{lim}[1-\frac{1}{N}]\\ & =1\end{array}$$

$\mathrm{△}$

Integrales de este tipo suelen abundar en física y probabilidad. ¿Habrá algún modo de manejar este tipo de integrales de forma unificada?

Fue precisamente por esta clase de restricciones que a finales del siglo XIX se empezaron a buscar nociones distintas o más generales de integración. Fue precisamente Henri Lebesgue quien en 1901 publicó su famoso artículo Sur une généralisation de l’intégrale définie, en el que definía una noción de integración que generalizaba a la de Riemann y resolvía varias de las limitaciones que esta presentaba.

La teoría de integración de Lebesgue y la teoría de la medida han sido tremendamente exitosas en el análisis moderno y ha encontrado aplicaciones fundamentales en áreas como la probabilidad, las ecuaciones diferenciales, la física matemática, entre otras.

Más adelante…

Abordaremos el problema de la medida sobre los conjuntos más sencillos: los rectángulos. Veremos algunos resultados técnicos que utilizaremos a lo largo de la construcción de la medida de Lebesgue.