Sea $f : \mathbb{R}^2 \rightarrow \mathbb{R}^2$ dada por

$$f (x, y) = \big( u (x, y), v (x, y) \big) = \big( e^x \cos y, e^x \sin y \big)$$

Además, $f$ es de clase $\mathcal{C}^1$.

Para todo $\vec{a} = x_0, y_0)$ podemos calcular la matriz jacobiana

${f\, }’ (\vec{a}) = \begin{pmatrix} \dfrac{\partial u}{\partial x}(\vec{a}) & \dfrac{\partial u}{\partial y}(\vec{a}) \\ \\ \dfrac{\partial v}{\partial x}(\vec{a}) & \dfrac{\partial v}{\partial y}(\vec{a}) \end{pmatrix} = \begin{pmatrix} e^{x_0} \cos y_0 & – \, e^{x_0} \sin y_0 \\ \\ e^{x_0} \sin y_0 & e^{x_0} \cos y_0 \end{pmatrix}$

Entonces el $det \, {f \, }’ (\vec{a}) = e^{2x_0} \, > \, 0$ para todo $(x_0, y_0)$.

Por lo que, $f$ cumple las hipótesis del teorema de la función inversa, $det \, {f \, }’ (\vec{a}) \neq 0$.

Existen abiertos $\mathcal{U} \subseteq \mathbb{R}^2$ y $\mathcal{V} \subseteq \mathbb{R}^2$ tales que $\vec{a} \in \mathcal{U}$, $f(\vec{a}) \in \mathcal{V}$.

Entonces $f \Big|_{\mathcal{U}} : \mathcal{U} \rightarrow \mathcal{V}$ es invertible, existe la inversa localmente, y la inversa es derivable $\big( {f\, }^{-1}\big)’ (b) = \Big( {f\, }’ \big( {f\, }^{-1} (b) \big) \Big)^{-1}$.

La condición de que $det \, {f\, }’ (\vec{a}) \neq 0 $ garantiza que la diferencial de $f$ en $\vec{a}$ sea un transformación lineal invertible.

$$df_{\vec{a}}: \mathbb{R}^2 \rightarrow \mathbb{R}^2$$

Entonces, ¿cuál es la imagen de una recta horizontal $y = y_0$ bajo $f$?

$f (x, y_0) = e^x (\cos y_0, \sin y_0)$ con $x$ variable y $ y = y_0$ fija. Entonces $(\cos y_0, \sin y_0)$ es un vector constante. Y $e^x \in (0, \infty)$.

Si $y_0 = \pi$ entonces, $(\cos y_0, \sin y_0) = (- \, 1, 0)$.

Si $y_0 = \, – \, \pi$ entonces, $(\cos y_0, \sin y_0) = (- \, 1, 0)$

Ahora, ¿cuál es la imagen de una recta vertical $x = x_0$?

Es decir, $x = x_0$ fija, y $y$ variable. Entonces

$f (x_0, y) = e^{x_0} ( \cos y, \sin y)$, donde $e^{x_0}$ es constante, y $( \cos y, \sin y)$ es un vector unitario variable.

En la siguiente animación puedes modificar los valores de $x_0$ y $y_0$ para observar la imagen respectiva de las rectas horizontales y verticales que se analizaron anteriormente.

https://www.geogebra.org/classic/wfh2bbkb

Tomemos un punto $\vec{a} = (x_0, y_0)$.

Tomemos un punto cercano $\vec{a} + \vec{h} = (x_0 + \Delta x , y_0 + \Delta y)$

Observemos el rectangulito en el plano $XY$ delimitado por las rectas $x = x_0$, $x = x_0 + \Delta x$, $y = y_0$ y $y = y_0 + \Delta y$.

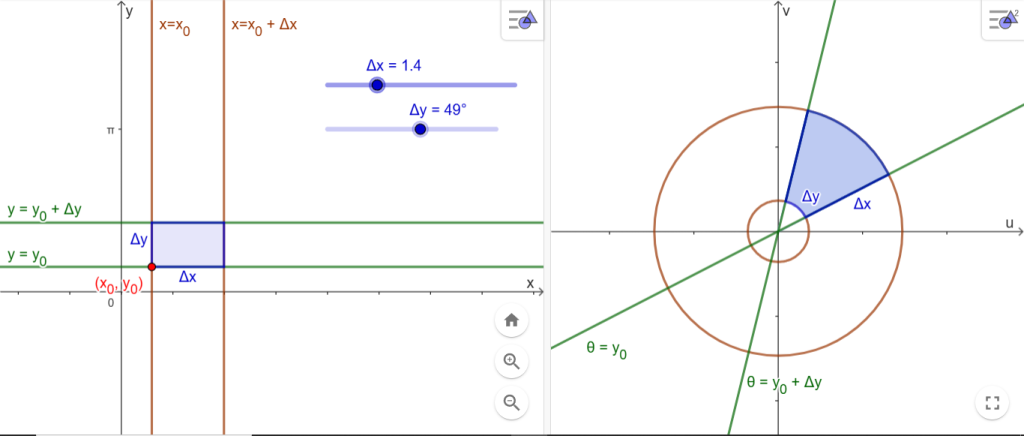
¿Cuál es el área de este sector circular?

Siguiendo el razonamiento anterior, el área buscada es

$\Big( e^{2(x_0 + \Delta x)} \, – \, e^{2x_0} \Big) \dfrac{\Delta y}{2} = e^{2x_0} \Big( e^{2 \Delta x} \, – \, 1 \Big) \dfrac{\Delta y}{2}$.

La razón entre el área del sector de corona circular y el área del rectángulo es:

$\dfrac{e{2x_0} \Big( e^{2 \Delta x} \, – \, 1\Big) \cancel{\Delta y}}{2 \Delta x \cancel{\Delta y}} \rightarrow e^{2x_0}$

Si consideramos $t=2\Delta x$ , entonces la razón anterior es

$\dfrac{e^t \, – \, 1}{t} =\dfrac{e^x \, – \, 1}{x} = \dfrac{ f(x) \, – \, f(0)}{x \, – \, 0} \rightarrow e^0 = 1$

$f (x, y) = \Big( e^x \cos y, e^x \sin y \Big) = (u, v) $

$f’ (a) = \begin{pmatrix} e^x_0 \cos y_0 & \, – \, e^x_0 \sin y_0 \\ \\ e^x_0 \sin y_0 & e^x_0 \cos y_0 \end{pmatrix}$

Consideremos

$\alpha : \mathbb{R} \rightarrow \mathbb{R}^2$ una curva que pasa por $a$, tal que $\alpha (0) = a$.

Y sea $f \circ \alpha : \mathbb{R} \rightarrow \mathbb{R}^2$ tal que

$( f \circ \alpha) (0) = f ( \alpha (0) ) = f (a)$; donde $f \circ \alpha$ es una curva que pasa por $f (a)$.

Por la regla de la cadena

$\Big( f \circ \alpha \Big)’ (0) = f’ \big( \alpha (0) \big) {\alpha \, }’ (0) = f’ \big( a \big) {\alpha \, }’ (0)$

La diferencial de $f$ en $a$

$d f_a : \mathbb{R}^2 \rightarrow \mathbb{R}^2$ es tal que los vectores tangentes a curvas que pasan por $a$, $\longrightarrow$ vectores tangentes a curvas que pasan por $f (a)$

$\vec{v} = {\alpha \, }’ (0) \longrightarrow f’ (a) \cdot \alpha’ (0) = \vec{w}$

Curva

$\begin{align*} {\alpha \, } (t) = (x_0 + t, y_0) & \hspace{2cm} {\alpha \, }’ (t) = (1, 0) \\ \\ {\alpha \, } (0) = (x_0 , y_0) & \hspace{2cm} {\alpha \, }’ (0) = (1, 0) \end{align*}$

$\Big( f \circ \alpha \Big) (t) = f \Big( \alpha (t) \Big) = \Big( e^{x_0 + t} \cos y_0, e^{x_0 + t} \sin y_0 \Big)$

$\Big( f \circ \alpha \Big)’ (t) = \Big( e^{x_0 + t} \cos y_0, e^{x_0 + t} \sin y_0 \Big)$

$\Big( f \circ \alpha \Big)’ (0) = \Big( e^{x_0} \cos y_0, e^{x_0} \sin y_0 \Big)$

$\begin{align*} {\beta \, } (t) = (x_0 , y_0 + t) & \hspace{2cm} {\beta \, }’ (0) = (0, 1) \\ \\ {\beta \, } (0) = (x_0 , y_0) & \end{align*}$

$\Big( f \circ \beta \Big) (t) = f \Big( \beta (t) \Big) = \Big( e^{x_0 } \cos (y_0 + t), e^{x_0 } \sin (y_0 + t) \Big)$

$\Big( f \circ \beta \Big)’ (t) = \Big( \, – \, e^{x_0} \sin (y_0 + t), e^{x_0} \cos (y_0 + t) \Big)$

$\Big( f \circ \beta \Big)’ (0) = \Big( \, – \, e^{x_0} \sin y_0 , e^{x_0} \cos y_0 \Big)$

$(u, v) = \big( e^x \cos y, e^x \sin y \big)$

$\begin{pmatrix} e^{x_0} \cos y_0 & \, – \, e^{x_0} \sin y_0 \\ \\ e^{x_0} \sin y_0 & e^{x_0} \cos y_0 \end{pmatrix} = e^{x_0} \begin{pmatrix} \cos y_0 & \, – \, \sin y_0 \\ \\ \sin y_0 & \cos y_0 \end{pmatrix} = \begin{pmatrix} e^{x_0} & 0 \\ \\ 0 & e^{x_0} \end{pmatrix} \begin{pmatrix} \cos y_0 & \, – \, \sin y_0 \\ \\ \sin y_0 & \cos y_0 \end{pmatrix}$

$f (x, y) = \big( u (x, y), v (x, y) \big) = \Big( e^x \cos y, e^x \sin y \Big)$ cumple las hipótesis del teorema de la función inversa en todos los puntos $a = (x_0, y_0) \in \mathbb{R}^2$.

El teorema nos garantiza que existe una inversa local, es decir, una vecindad $\mathcal{U}$ que contiene a $a$ y una vecindad $\mathcal{V}$ que contiene a $f (a)$ tal que $f \big|_{\mathcal{U}} : \mathcal{U} \rightarrow \mathcal{V}$ es biyectiva e invertible tiene inversa local $f^{-1} : \mathcal{V} \rightarrow \mathcal{U}$.

Tomemos $a = (0, 0)$ y $f (a) = (1, 0)$.

Para describir con detalle la inversa local de la que nos habla el teorema necesitamos saber cuales son los abiertos $\mathcal{U}$ y $\mathcal{V}$, y la regla de correspondencia $x = p (u, v)$ y $y = q (u, v)$.

$u = e^x \cos y$

$v = e^x \sin y$

Entonces

$u^2 + v^2 = e^{2x} {\cos}^2 y + e^{2x} {\sin}^2 y = e^{2x}$

$ln (u^2 + v^2) = ln (e^{2x}) = 2x$

$\textcolor{blue}{x = \dfrac{ln (u^2 + v^2)}{2}}$ siempre que $\textcolor{blue}{(u, v) \neq (0, 0)}$

$\dfrac{v}{u} = \dfrac{e^x \sin y}{e^x \cos y} = \tan y$

$\textcolor{blue}{y = \arctan \dfrac{v}{u}}$ siempre que $\textcolor{blue}{u \neq 0}$

Además

$f (x, y) = \big( e^x \cos y, e^x \sin y \big)$

$\Big\| f (x, y) \Big\|^2 = e^{2x} > 0$

Sea $\mathcal{U} = \Big\{ (x, y) \in \mathbb{R}^2$ tales que $\, – \, \frac{\pi}{2} < y < \frac{\pi}{2} \Big\}$;

entonces $\mathcal{V} = \Big\{ (u, v) \in \mathbb{R}^2$ tales que $u > 0 \Big\}$

Dibujo A preguntar

$f’ (a) = \begin{pmatrix} \dfrac{\partial u}{\partial x} & \dfrac{\partial u}{\partial y} \\ \\ \dfrac{\partial v}{\partial x} & \dfrac{\partial v}{\partial y} \end{pmatrix} = \begin{pmatrix} e^x \cos y & \, – \, e^x \sin y \\ \\ e^x \sin y & e^x \cos y \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ \\ 0 & 1 \end{pmatrix}$ para $a = (0, 0)$……$(1)$

$b = f (a) = (1, 0) = (u, v)$

$\Big(f^{-1} \Big)’ (b) = \begin{pmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ \\ 0 & 1 \end{pmatrix}$…….$(2)$

Luego de $(1)$ y $(2)$ podemos concluir que

$$\Big(f^{-1} \Big)’ (b) = f’ (a)$$

Preguntar por los demás dibujos y el último problema de las fotos