Tres alelos ( formas naturales de genes) $A$, $B$ y $O$ determinan los tres tipos sanguíneos.

$$ \begin{align*} A &\iff (AA \, \, \circ \, \, AO ) \\ B &\iff (BB \, \, \circ \, \, BO) \\ O &\iff ( OO) \\ AB &\iff ( AB ) \end{align*}$$

La ley de Hardy – Weinberg establece que la proporción $P$ de individuos de una población que llevan los alelos diferentes está dada por la expresión:

$$P = 2pq \, + \, 2pr \, + \, 2qr$$

donde $p$, $q$ y $r$ son las proporciones de alelos $A$, $B$ y $O$ en dicha población.

Use el hecho de que $ p + q + r = 1$ para demostrar que $p \leq \dfrac{2}{3}$

(Nótese que la proporción de individuos en la población que lleva dos alelos iguales es $ p^2+q^2+r^2$)

Maximizar $P = 2pq \, + \, 2pr \, + \, 2qr$ sujeta a $ p + q + r = 1$,

restricción $ Q (p, q, r) = p + q + r \, – \, 1 = 0$, con $p, q, r, \geq 0$

Usando multiplicadores de Lagrange $\nabla P = \Bigg( \dfrac{\partial P}{\partial p}, \dfrac{\partial P}{\partial q}, \dfrac{\partial P}{\partial r} \Bigg)$ entonces,

$\nabla P = \big( 2q + 2r , 2p + 2r , 2p + 2q \big)$

$\nabla Q = ( 1 , 1, 1 )$

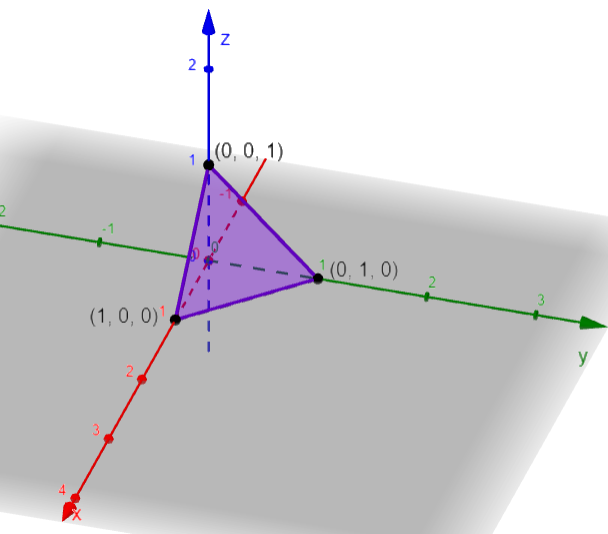
Vamos a examinar en qué puntos del triángulo la función $P(p,q,r)$ alcanza sus valores extremos.

a) ¿Qué pasa en el interior del simplejo (triángulo)?

b) ¿Qué pasa en las aristas?

c) ¿Qué pasa en los vértices?

a) Si un valor extremo se alcanza en el interior del triángulo, entonces lo podemos encontrar con el método de multiplicadores de Lagrange con una restricción. $$\nabla P = \lambda \nabla Q$$

$\begin{pmatrix} 2q + 2r \\ \\ 2p + 2r \\ \\ 2p + 2q \end{pmatrix} = \lambda \begin{pmatrix} 1 \\ \\ 1 \\ \\ 1 \end{pmatrix}$

$\begin{align*} 2q + 2r &= \lambda\\ \\ 2p + 2r &= \lambda \\ \\ 2p + 2q &= \lambda \end{align*}$

Sumando

$4p + 4q + 4r = 3 \lambda$

$4 ( p + q + r) = 3 \lambda$, como $ p + q + r = 1$, entonces

$4 = 3 \lambda$ por lo que $\lambda = \dfrac{4}{3}$

Luego, sustituyendo en el sistema anterior se tiene que:

$$p = \dfrac{1}{3}\, , \, q = \dfrac{1}{3} \, , \, r = \dfrac{1}{3}$$

Entonces

$P \Bigg( \dfrac{1}{3}, \dfrac{1}{3}, \dfrac{1}{3} \Bigg) = 2 \Bigg( \dfrac{1}{9} \Bigg) + 2 \Bigg( \dfrac{1}{9} \Bigg) + 2 \Bigg( \dfrac{1}{9} \Bigg) = \dfrac{6}{9} = \dfrac{2}{3}$

c) En los vértices evaluamos el valor de la función, porque ahí también puede haber un valor extremo:

$P ( 1, 0, 0) = 0$

$P ( 0, 1, 0) = 0$

$P ( 0, 0, 1) = 0$

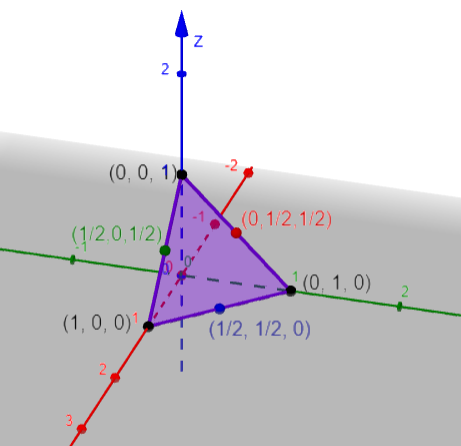
b) En este caso, en cada arista una variable es constante, y podemos reducir el problema a encontrar los valores extremos de una función de dos variables sujeta a una restricción, de nuevo, usaremos multiplicadores de Lagrange.

Hay tres aristas, cuando $p = 0$, $q = 0$ o $r = 0$

Analicemos que sucede si $r = 0$, entonces $P (p, q, 0) = 2pq$

Ahora el problema es maximizar $2pq$, sujeta a $ p + q = 1$ con $p, q \geq 0$, entonces

$ p = q = \frac{1}{2}$ y $P (\frac{1}{2}, \frac{1}{2}, 0) = \frac{1}{2}$

Análogamente para las otras aristas se obtienen los puntos $ (0, \frac{1}{2}, \frac{1}{2})$ y $ (\frac{1}{2}, 0, \frac{1}{2})$, donde $P$ para cada uno de ellos es $\frac{1}{2}$.

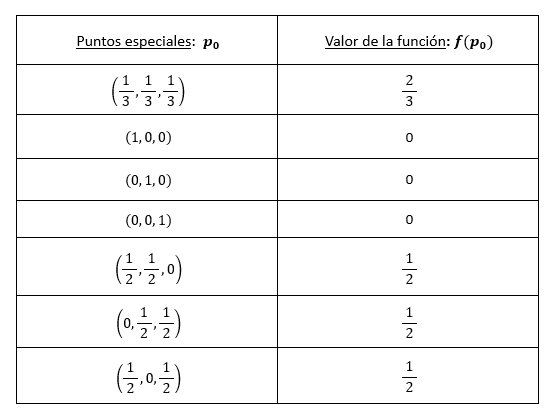
En la siguiente tabla puedes observar el valor de la función en cada uno de los puntos especiales analizados: vértices, puntos medios de los lados y el punto calculado en el inciso (a) $\Big( \dfrac{1}{3}, \dfrac{1}{3}, \dfrac{1}{3} \Big)$.

Por lo tanto, de lo analizado anteriormente vemos que el valor máximo de $P$ es $\frac{2}{3}$ y se obtiene en el punto $ \Bigg( \dfrac{1}{3}, \dfrac{1}{3}, \dfrac{1}{3} \Bigg)$.