Si una curva está dada por la gráfica de una función $\mathbb{R} \rightarrow \mathbb{R}$

$$\Gamma := \big\{ (x, y) \in \mathbb{R}^2 \big| y = f (x) \big\}$$

Donde, $\alpha (t) = (t, f (t)) $, y

${\alpha}’ (t) = ( 1, f’ (t) ).$

Además, $\big\|{\alpha}’ (t) \big\| = \sqrt{ 1 + (f’ (t_0) )^2}$

Observación: Con esta parametrización la rapidez $\big\|{\alpha}’ (t) \big\| \geq 1$ solo puede ser $\big\|{\alpha}’ (t) \big\| \equiv 1$ en el caso $f’ (t) \equiv 0.$

Fórmula para la curvatura

$$ \mathcal{K} = \dfrac{\begin{vmatrix} x’ & {x}^{\prime \prime} \\ y’ & {y}^{\prime \prime} \end{vmatrix}}{\big\|{\alpha}’ (t) \big\|^3}$$

Como $\begin{align*} x (t) &= t & x’ (t) &= 1 & {x}^{\prime \prime} (t) &= 0\\ y (t) &= f (t) & y’ (t) &= f’ (t) & {y}^{\prime \prime} (t) &= {f}^{\prime \prime} (t) \end{align*}$

Entonces

$$ \mathcal{K} = \dfrac{\begin{vmatrix} 1 & 0 \\ f’ (t) & { f}^{\prime \prime} (t) \end{vmatrix}}{\sqrt{\big(1 + (f’ (t))^2 \big)}^3}$$

Luego

$$ \mathcal{K} = \dfrac{ { f}^{\prime \prime} (t) }{\Big(1 + (f’ (t))^2 \Big)^3}$$

para una curva dada como la gráfica de una función.

${}$

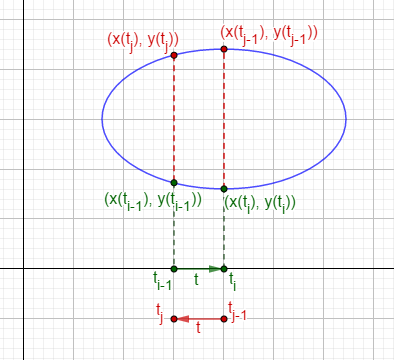
Una forma para calcular el área encerrada por una curva simple, cerrada, parametrizada y plana.

Vamos a tratar de calcular el área usando sumas de Riemann de la forma $$\sum f (\xi_i) \Delta t_i$$

Para el «rectángulo» pequeño tenemos que

Base $\Delta x_i = x (t_i) \, – \, x (t_{i-1})$

Altura $y (\xi_i)$

Entonces, el área es

$A_1 = y (\xi_i) \big( x (t_i) \, – \, x (t_{i-1})\big)$

Para el «rectángulo» grande tenemos que

Base $\Delta x_j =\, – \, \big( x (t_j) \, – \, x (t_{j-1}) \big)$

Altura $y (\xi_j)$

Entonces, el área es

$A_2 = y (\xi_j) \Big( \, – \, \big( x (t_j) \, – \, x (t_{j-1})\big) \Big)$

Luego el área total es

$$ A = \, – \, \Big( y (\xi_j) \Delta x_j + y (\xi_i) \Delta x_i \Big)$$

$$ A = \, – \, \sum y (\xi_i) (\Delta x_i) = \, – \, \sum y (\xi_i) \dfrac{dx}{dt} (\Delta t)$$

Por lo tanto $$ A = \, – \, \int_a^b y (t) \dfrac{dx}{dt} \Delta t$$

donde

$\Delta x_i = x (t_i) \, – \, x (t_{i-1})$

$\dfrac{\Delta x_i }{\Delta t_i} = \dfrac{x (t_i) \, – \, x (t_{i-1})}{t_i \, – \, t_{i-1}}$

$\Delta x_i = \dfrac{\Delta x_i}{\Delta t_i} \Delta t_i$

Luego $$A = \dfrac{1}{2} \int_a^b \Bigg( x \dfrac{dy}{dt} \, – \, y \dfrac{dx}{dt} \Bigg)$$

$$ A = \dfrac{1}{2} \begin{vmatrix} x & \dfrac{dx}{dt}\\ y & \dfrac{dy}{dt} \end{vmatrix}$$