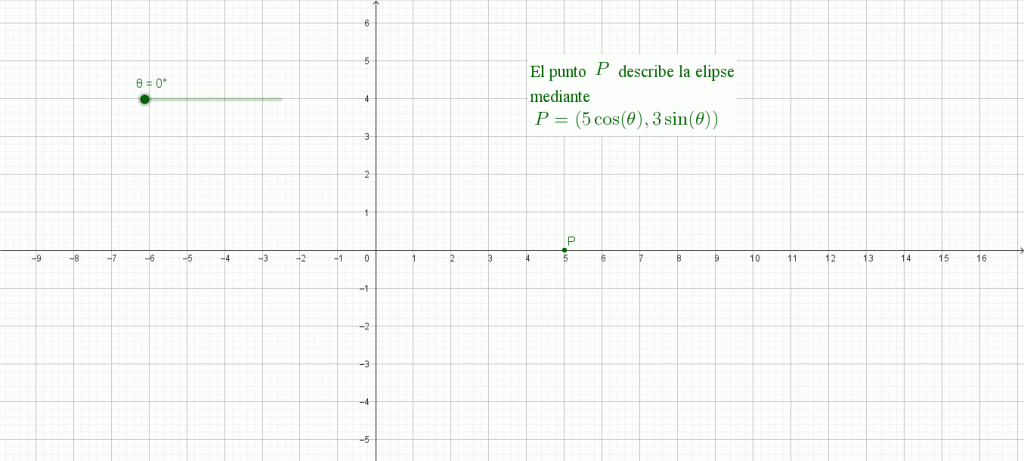
Elipse

La elipse : $$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$$

se puede parametrizar como

$$\left\{ x = a \cos \theta \atop y = b \sin \theta \right.$$

ya que si elevamos al cuadrado ambas ecuaciones obtenemos que $$\left\{ x^2 = a^2 \cos^2 \theta \atop y^2 = b^2 \sin^2 \theta \right.$$ luego, despejando y sumando miembro a miembro observamos que $$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = \cos^2 \theta + \sin^2 \theta = 1$$ que es la ecuación de la elipse.

En el siguiente enlace puedes observar una animación de la elipse.

https://www.geogebra.org/classic/vntpwfrh

Hipérbola

La hipérbola: $$x^2 – y^2 = 1$$

se puede parametrizar como

$$\left\{ x = \sec \theta \atop y = \tan \theta \right.$$

ya que si elevamos al cuadrado cada ecuación tenemos que $$\left\{ x^2 = \sec^2 \theta \atop y^2 = \tan^2 \theta \right.$$ luego, restándolas vemos que $$ x^2 – y^2 = \sec^2 \theta – \tan^2 \theta = \dfrac{1}{\cos^2 \theta} – \dfrac{\sin^2 \theta}{\cos^2 \theta} = \dfrac{1 – \sin^2 \theta}{\cos^2 \theta} = \dfrac{\cos^2 \theta}{\cos^2 \theta} = 1 $$ obtenemos la ecuación de la hipérbola.

Otra manera de parametrizar la hipérbola es considerando

$$\left\{ x = \cosh \theta = \dfrac{e^t + e^{-t}}{2} \atop y = \sinh \theta = \dfrac{e^t – e^{-t}}{2}\right.$$

$$ x^2 – y^2 = \cosh^2 \theta – \sinh^2 \theta = 1$$

En el siguiente enlace puedes observar una animación de la hipérbola.

https://www.geogebra.org/classic/b3wbbndx

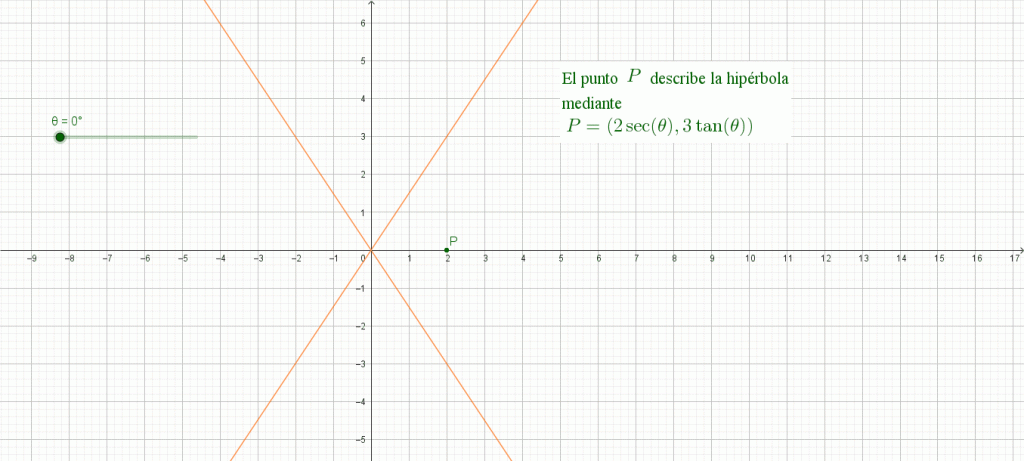
Longitud de arco

Consideramos una curva parametrizada $$\alpha : [a, b] \subset \mathbb{R} \rightarrow \mathbb{R}^2$$ $$\alpha (t) =(x(t), y(t))$$

Sean $P = \alpha (a)$

y $Q = \alpha (b)$

¿Cuál es la longitud de arco desde $P$ hasta $Q$?

• Aproximemos la longitud de la curva como suma de segmentos de recta.

Dibujo A

$\sum\limits_{i = 1}^n \|\alpha (t_i) – \alpha (t_{i-1}) \|$ con la partición $ a = t_0 < t_1 < \dots < t_n = b$

Nos preguntamos si hay un teorema del valor medio. Es decir, existe $\rho \in (a, b)$ tal que $$f(\rho) = \dfrac{f(b) – f(a)}{b – a}$$

Entonces existe $\rho \in (a, b)$ tal que $$\overrightarrow{\alpha}(\rho) = \dfrac{\overrightarrow{\alpha}(b) – \overrightarrow{\alpha}(a)}{b – a} $$

Si así fuera, entonces $$\| {\alpha}'(\rho) \| = \dfrac{\| \overrightarrow{\alpha}(b) – \overrightarrow{\alpha}(a) \|}{b – a} $$

$\sum\limits_{i = 1}^n \|\alpha (t_i) – \alpha (t_{i-1}) \|=\sum\limits_1^n \|\alpha (t_i) – \alpha (t_{i-1}) \|\dfrac{t_i – t_{i-1}}{t_i – t_{i-1}} $

$=\sum\limits_{i = 1}^n \|{\alpha}’ (\xi_i) \| (t_i – t_{i-1})$

Por lo anterior definimos la longitud de arco desde $P$ hasta $Q$ como

$$ \int\limits_a^b \| {\alpha}'(t) \| dt $$

CASO CIRCUNFERENCIA

Para $\omega = 1.$

$x (t) = A \cos (t) + h$

$y (t) = A \sin (t) + k$

Derivando

$x’ (t) = – A \sin (t) \Longrightarrow (x’)^2 (t) = A^2 \sin^2 (t)$

$y’ (t) = A \cos (t) \Longrightarrow (y’)^2 (t) = A^2 \cos^2 (t) $

Sumando ambas igualdades

$(x’)^2 + (y’)^2 = A^2$ por lo que $\| {\alpha}'(t) \| = A.$

Si $P = \alpha (\theta_0)$ y $Q = \alpha (\theta_1)$, entonces

$$ \int\limits_{\theta_0}^{\theta_1} A \, dt = A (\theta_1 – \, \theta_0) = \text{radio } \Delta \theta $$

Una parametrización de una curva en coordenadas polares

Sea $r = f (\theta) $

Donde $\theta = \omega t$ y $ r = f( \omega t)$, que en coordenadas polares es:

$x (t) = f (\omega t) \cos (\omega t)$

$y (t) = f (\omega t) \sin (\omega t)$

Si $\omega = 1$ entonces $\overrightarrow{\alpha} (t) = (x(t), y(t)) = x (t) \vec{e_1} + y (t) \vec{e_2} = r (t) \overrightarrow{\beta} (t)$, donde $\beta (t) = (\cos \theta (t), \sin \theta (t))$

En este caso, ¿cómo calculamos la velocidad?

$x’ (t) = \dfrac{d}{dt} (f(\omega t) \cos (\omega t)) = \omega f'(\omega t) \cos (\omega t) – \sin (\omega t) f(\omega t) \omega$

$y’ (t) = \dfrac{d}{dt} (f(\omega t) \sin (\omega t)) = \omega f'(\omega t) \sin (\omega t) + \cos (\omega t) f (\omega t) \omega$

Luego,

$(x’, y’) = ( \omega f'(\omega t) \cos (\omega t) – \sin (\omega t) f(\omega t) \omega , \omega f'(\omega t) \sin (\omega t) + \cos (\omega t) f(\omega t) \omega )$

$(x’, y’) = \omega f'(\omega t) (\cos (\omega t) , \sin (\omega t) + \omega f(\omega t) ( -\sin (\omega t) , \cos (\omega t)$

$\overrightarrow{\alpha}’ (t) = r’ (t) \overrightarrow{\beta} (t) + r (t) \overrightarrow{\beta}’ (t)$

$\beta$, $\beta’$ son una base de $\mathbb{R}^2$ en la que podemos extresar ${\alpha}’$.

$\vec{e_1}$, $\vec{e_2}$ son otra base de $\mathbb{R}^2$ en la que también podemos extresar ${\alpha}’$.

Luego, $\alpha’ (t) = x’ (t) \vec{e_1} + y’ (t) \vec{e_2} = r’ (t) \overrightarrow{\beta} (t) + r (t) \overrightarrow{\beta}’ (t)$