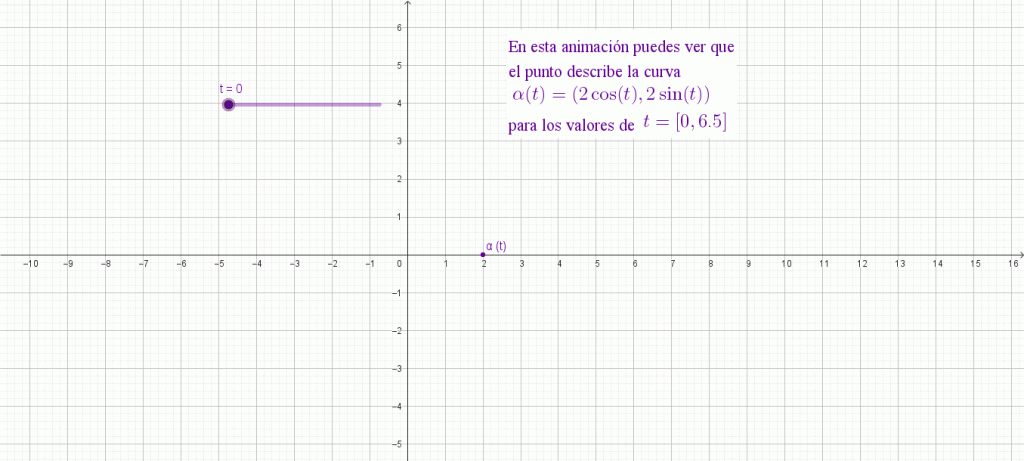
Dada una circunferencia de radio $r>0$ con centro en $(h,k)$, posición inicial $(x_0,y_0)$ y velocidad inicial $(x_0^{\prime },y_0^{\prime })$, analizamos diferentes casos para poder calcular su frecuencia, velocidad angular, periodo, amplitud y fase.

Caso sencillo

Radio $r=1$

Centro $(h,k)=(0,0)$

Posición inicial $(x_0,y_0)=(1,0)$

Velocidad inicial $(x_0^{\prime },y_0^{\prime })=(0,1)$

Entonces $\{\genfrac{}{}{0ex}{}{x(t)=\cos (t)}{y(t)=\sin (t)}$

Tenemos que la rapidez unitaria es $\Vert {\alpha }^{\prime }(t)\Vert =1.$

Si el periodo es $2\pi$ entonces, para toda $t$:

$\{\genfrac{}{}{0ex}{}{x(t+2\pi )=x(t)}{y(t+2\pi )=y(t)}$

Por lo que $\overrightarrow{\alpha }(t)=\overrightarrow{\alpha }(t+2\pi ).$

¿Cómo serian las ecuaciones si el movimiento fuera de $periodo1$?

$\{\genfrac{}{}{0ex}{}{x(t)=\cos (2\pi t)}{y(t)=\sin (2\pi t)}$

Entonces para $t=0$ la posición es $(1,0)$; y para $t=1$ la posición también es $(1,0).$

Luego, la rapidez de $\{\genfrac{}{}{0ex}{}{x(t)=\cos (2\pi t)}{y(t)=\sin (2\pi t)}$ es

$\{\genfrac{}{}{0ex}{}{x^{\prime }(t)=-2\sin (2\pi t)}{y^{\prime }(t)=2\cos (2\pi t)}$

Por lo que $\Vert (x^{\prime }(t),y^{\prime }(t))\Vert =\sqrt{(2\pi {)}^2({\cos }^2(2\pi t)+{\sin }^2(2\pi t))}$,

es decir que la rapidez es: $$\Vert (x^{\prime }(t),y^{\prime }(t))\Vert =2\pi$$

Para periodos $T>0$

$\{\genfrac{}{}{0ex}{}{x(t)=\cos \left(\frac{2\pi t}{T}\right)}{y(t)=\sin \left(\frac{2\pi t}{T}\right)}$

Entonces para $t=0$ la posición es $(1,0)$; y para $t=T$ la posición también es $(1,0).$

¿Cómo serían las ecuaciones si recorremos la circunferencia en el sentido horario, con periodo $T=2\pi$?

Entonces $\{\genfrac{}{}{0ex}{}{x(t)=\cos (t)}{y(t)=–\sin (t)}$

Por lo que $(x^{\prime }(0),y^{\prime }(0))=(0,-1).$

Si ahora cambiamos la posición inicial, digamos que $\overrightarrow{p_0}=(x_0,y_0).$

Dado el punto $(x_0,y_0)$, existe un ángulo $\theta$ tal que:

$\{\genfrac{}{}{0ex}{}{x_0=\cos ({\theta }_0)}{y_0=\sin ({\theta }_0)}$

Si $(x_0,y_0)=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\Rightarrow {\theta }_0=45°=\frac{\pi }{4}$

Si $(x_0,y_0)=(\frac{1}{2},\frac{\sqrt{3}}{2})\Rightarrow {\theta }_0=60°=\frac{\pi }{3}$

Luego, para toda $t$ se tiene que:

$\{\genfrac{}{}{0ex}{}{x(t)=\cos (t+{\theta }_0)}{y(t)=\sin (t+{\theta }_0)}$

Cumple que $(x(0),y(0))=(\cos {\theta }_0,\sin {\theta }_0)=(x_0,y_0)$, es decir, en el instante $t_0=0$ la posición inicial es $(x_0,y_0).$

Si hubiéramos escrito

$\{\genfrac{}{}{0ex}{}{x(t)=\cos (t–{\theta }_0)}{y(t)=\sin (t–{\theta }_0)}$

Entonces $\{\genfrac{}{}{0ex}{}{x({\theta }_0)=1}{y({\theta }_0)=0}$ es decir, en el instante $t_0={\theta }_0$ la posición es $(1,0).$

Observación:

Si escribimos $\{\genfrac{}{}{0ex}{}{x(t)=\cos (–t)=cos(t)}{y(t)=\sin (–t)=–\sin (t)}$

entonces estamos recorriendo la circunferencia en sentido horario.

Ahora estudiemos el siguiente caso:

$\{\genfrac{}{}{0ex}{}{x(t)=\cos (wt)}{y(t)=\sin (wt)}$

El periodo es $\frac{2\pi }{T}=\omega \Rightarrow T=\frac{2\pi }{\omega }.$

Otro caso:

Si tenemos las ecuaciones $\{\genfrac{}{}{0ex}{}{x(t)=A\cos (wt)}{y(t)=A\sin (wt)}$

y $A=2$ entonces las ecuaciones

$\{\genfrac{}{}{0ex}{}{x(t)=2\cos (wt)}{y(t)=2\sin (wt)}$

representan una circunferencia de radio 2. $A$ se denomina amplitud.

Caso centro $(h,k)$

Si el centro está en el punto $(h,k)$, entonces:

$$\{\genfrac{}{}{0ex}{}{x(t)=A\cos (wt)+h}{y(t)=A\sin (wt)+k}$$

En las siguientes ventanas puedes observar una animación de la parametrización. En este caso la curva $\alpha (t)=(2\cos (t),2\sin (t))$