Dado un punto en coordenadas rectangulares $(x, y)$. ¿Cuáles son las coordenadas polares $( r, \theta)$? ¿Podemos despejar $(r, \theta)$ en función de $(x, y)$?
De $x^2 + y^2 = r ^2$, despejando $r$ se obtiene que $$r=\sqrt{x^2+y^2}$$
Para obtener el valor de $\theta$ tenemos dos maneras.
Una es usando la tangente $$\frac{y}{x} =\frac{r \sin \theta}{r \cos \theta} = \tan \theta$$ $$ \theta = \arctan \frac{y}{x}$$
Un detalle a tener en cuenta es que $x \neq 0$.
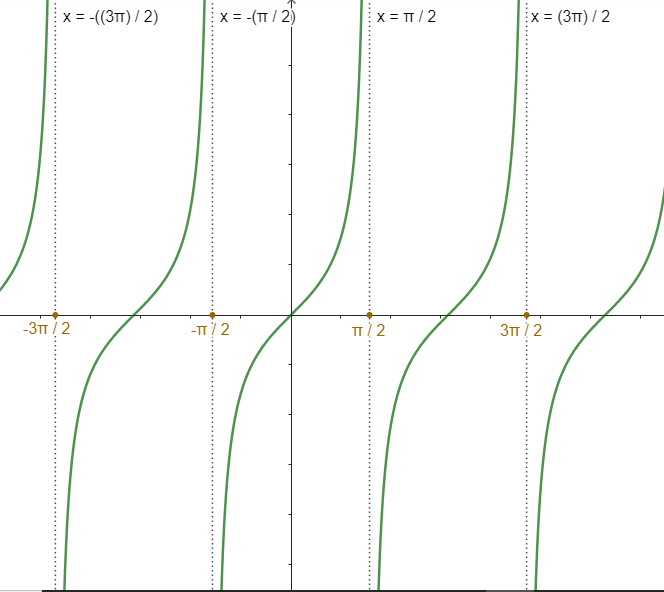
Además, podemos observar en la siguiente imagen que la función tangente $f(\theta) = \tan \theta$ tal que $f : \big(\frac{-\pi}{2}, \frac{\pi}{2}\big) \cup \big( \frac{\pi}{2}, \frac{3 \pi}{2}\big) \rightarrow \mathbb{R}$ no es inyectiva, y no tiene imagen inversa global, por lo que se debe elegir una rama, es decir un intervalo para el ángulo $\theta$.
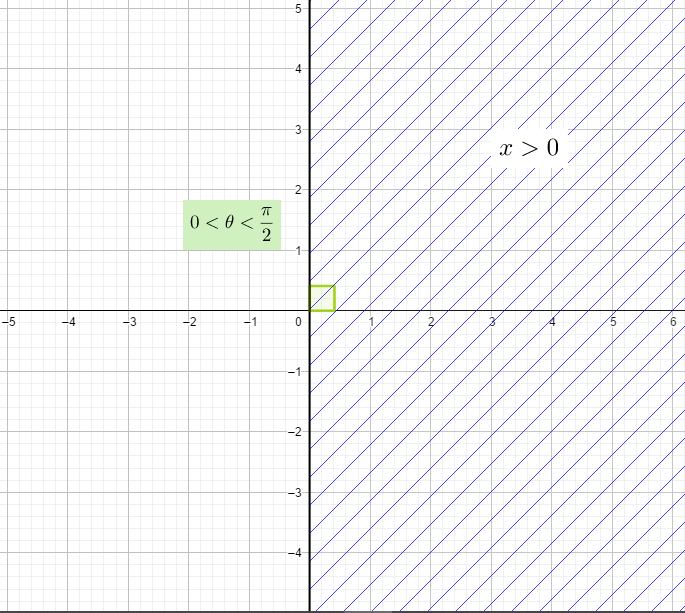
Si consideramos la rama $\frac{- \pi}{2}< \theta < \frac{\pi}{2}$, $f : \big(\frac{- \pi}{2}, \frac{ \pi}{2}\big) \rightarrow \mathbb{R}$ entonces la función $f(\theta) = \tan \theta$ si tiene función inversa $f^{-1} : \mathbb{R} \rightarrow \big(\frac{- \pi}{2}, \frac{ \pi}{2}\big)$ y por tanto la función $\arctan \big( \frac{y}{x} \big)$ toma valores en $\big(\frac{- \pi}{2}, \frac{ \pi}{2}\big)$.
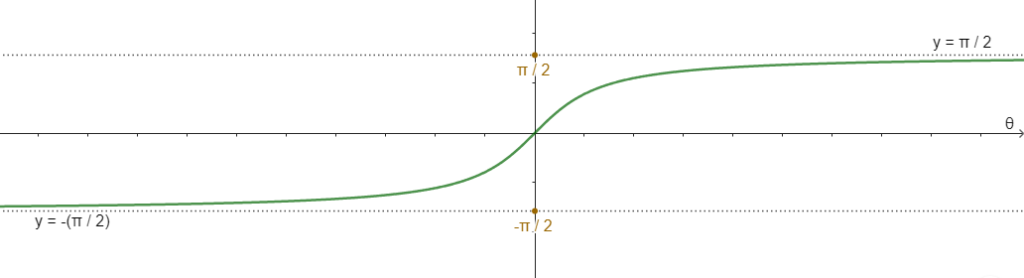
Es decir cuando $x > 0$.
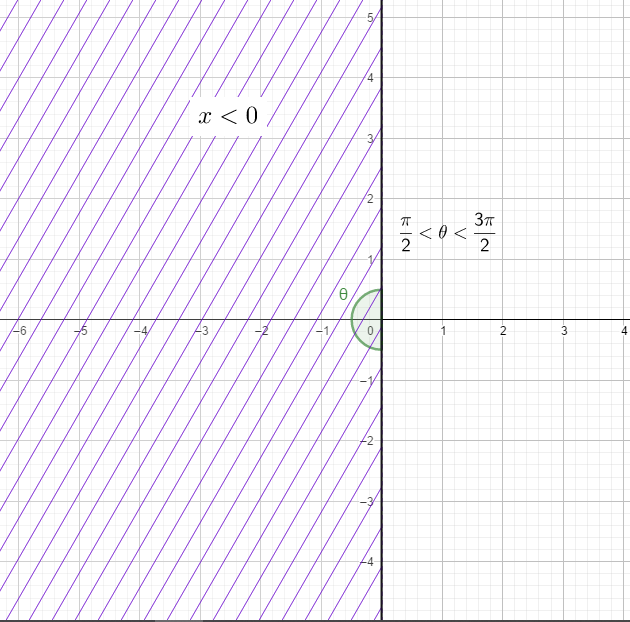
De manera análoga, si consideramos la rama $\frac{\pi}{2}< \theta < \frac{3 \pi}{2}$, $f : \big(\frac{3 \pi}{2}, \frac{ \pi}{2}\big) \rightarrow \mathbb{R}$ entonces la función $f(\theta) = \tan \theta$ si tiene función inversa $f^{-1} : \mathbb{R} \rightarrow \big(\frac{3 \pi}{2}, \frac{ \pi}{2}\big)$ y por tanto la función $\arctan \big( \frac{y}{x} \big)$ toma valores en $\big(\frac{3 \pi}{2}, \frac{ \pi}{2}\big)$.

Es decir para cuando $x < 0$.
Otra manera es la siguiente.
Despejando $(r, \theta)$ en términos de $(x, y)$ de la ecuación $$x^2 + y^2 = r ^2$$
Obtenemos que $$r= \sqrt{x^2+y^2}$$
Sustituyendo el valor de $r$ obtenido, en la ecuación $\cos{\theta} = \frac{y}{x}$ obtenemos que $\cos{\theta} = \frac{x}{\sqrt{x^2+y^2}}$ por lo que el valor de $\theta$ está dado por $$\theta = \arccos\left( \frac{x}{\sqrt{x^2+y^2}}\right)$$
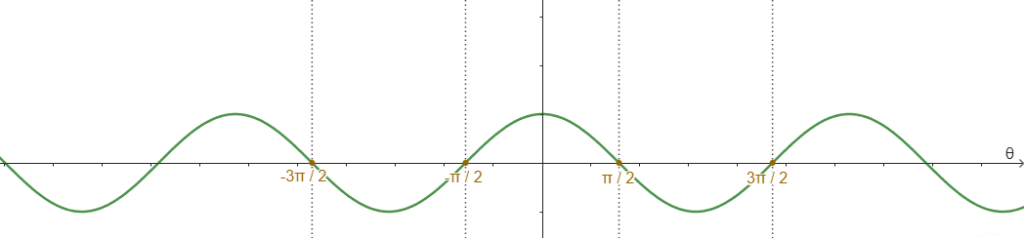
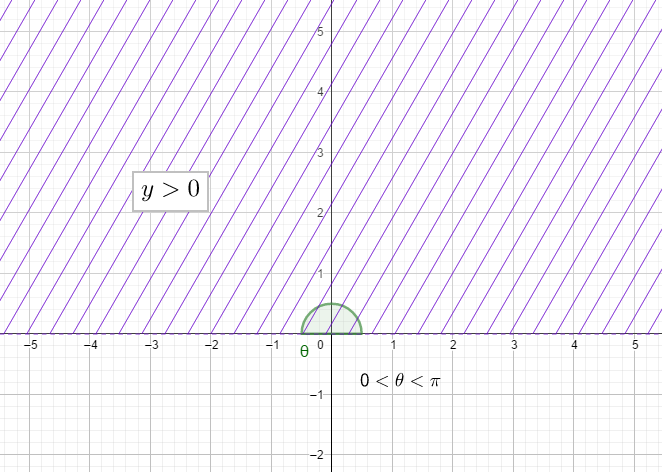
La función coseno tampoco es inyectiva sobre $\mathbb{R}$. Para poder hablar de la inversa hay que restringir el intervalo donde varia $\theta$.
Una opción es $0 < \theta < \pi$.
Es decir, se debe escoger el intervalo de $\theta$ que mejor nos permita calcular el ángulo dependiendo de donde se encuentre el punto $(x, y)$.
$$T : \mathbb{R}^2 \longrightarrow \mathbb{R}^2$$ $$(r, \theta) \longrightarrow (x, y)$$
Mediante tabulación.
Si fijamos $r_0 = 1$ y variamos $\theta$, tenemos que $x = r_0 \cos \theta$ entonces $x = \cos \theta$ y para $y = r_0 \sin \theta$ se obtiene $y = \sin \theta$. Luego $(x, y) = ( \cos \theta, \sin \theta)$.
Analíticamente para $r_0 = 1$ $$x^2+y^2=\cos^2 \theta + \sin^2 \theta$$ $$x^2+y^2=1$$
Por lo que la recta $r = 1$ en coordenadas polares es la circunferencia unitaria en coordenadas cartesianas.
Si fijamos $r_0 = 2$ y variamos $\theta$ se obtiene $$x^2+y^2=(2 \cos \theta)^2 + (2 \sin \theta)^2 = 4 \cos^2 \theta + 4 \sin^2 \theta = 4 (\cos^2 \theta + \sin^2 \theta) = 4$$
$$x^2+y^2=4$$
Por lo que la recta $r = 2$ en coordenadas polares es la circunferencia de radio 2 en coordenadas cartesianas.
Además, la recta $r = 0$ en coordenadas polares, es el punto $(0, 0)$ en coordenadas cartesianas.
https://www.geogebra.org/classic/rhv8nvwx
Ahora consideremos una recta horizontal $\theta = \theta_0$
$x = r \cos \theta_0$
$y = r \sin \theta_0$
$(x, y) = (r \cos \theta_0, r \sin \theta_0)$
$(x, y ) = r ( \cos \theta_0, \sin \theta_0)$
El factor $ (\cos \theta_0, \sin \theta_0)$ es constante, si variamos $r$ tenemos que:
* Si $r > 0$ la recta horizontal en coordenadas polares es un rayo que parte del origen en coordenadas cartesianas; pero si $r \in \mathbb{R} $ se transforma en la recta generada por el vector unitario $\vec{u} = (\cos \theta_0, \sin \theta_0)$.
En la siguiente animación dejamos fijo el ángulo y variamos el valor de $r$.
En la siguiente animación puedes variar al mismo tiempo $r, \Delta r, \theta$ y $\Delta \theta$ y observar las transformación en la segunda ventana.