Introducción

En la entrada anterior vimos como calcular la longitud de arco de una curva. Otra aplicación de las integrales es calcular el volumen de sólidos de revolución, por lo que en esta entrada se aprenderá a calcular el volumen de un sólido $S$ mediante secciones transversales o también llamado el método de los discos, además, veremos el método de las arandelas o también llamado el método de los anillos.

Superficies de revolución

Antes de comenzar a estudiar el método de los discos, definiremos lo que es una superficie de revolución.

Una superficie de revolución es una figura sólida que se obtiene al girar una curva plana alrededor de un eje que se encuentra en el mismo plano, a este eje se le conoce como eje de revolución. Veamos unos ejemplos.

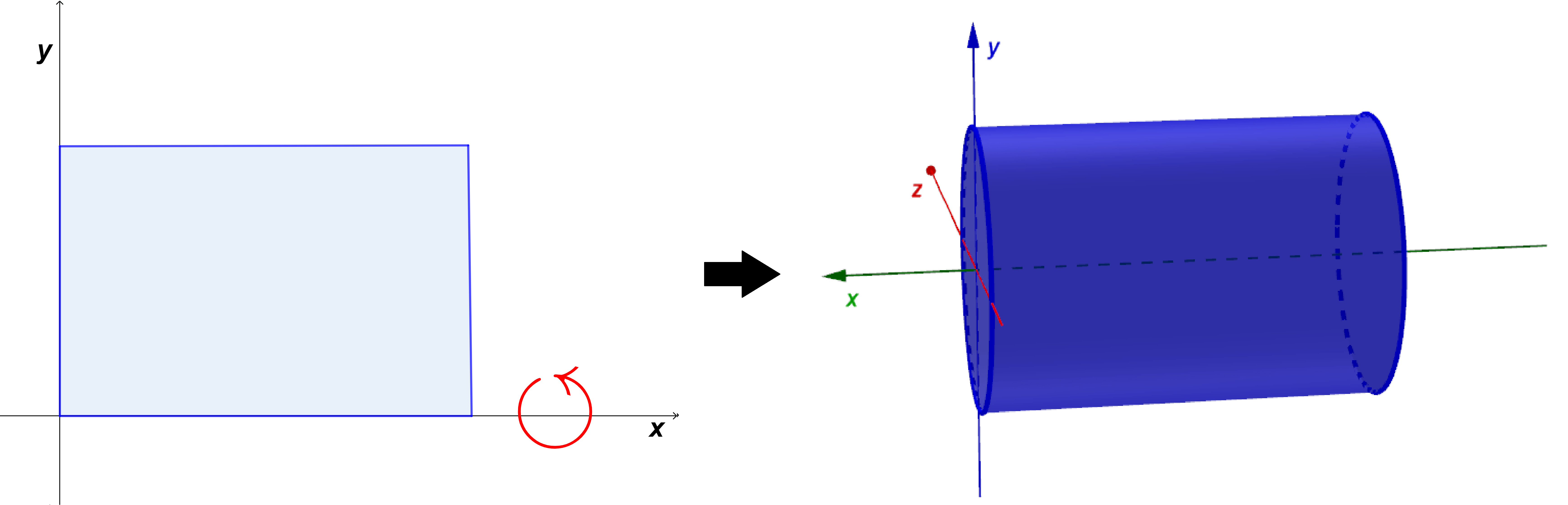
En la figura $(1)$ tenemos un rectángulo con altura y ancho, variables (figura de la izquierda), obsérvese que está en un plano, es decir, es una figura en 2 dimensiones, si nosotros hacemos girar esta figura alrededor del eje $x$ obtenemos un cilindro como en la figura de la derecha.

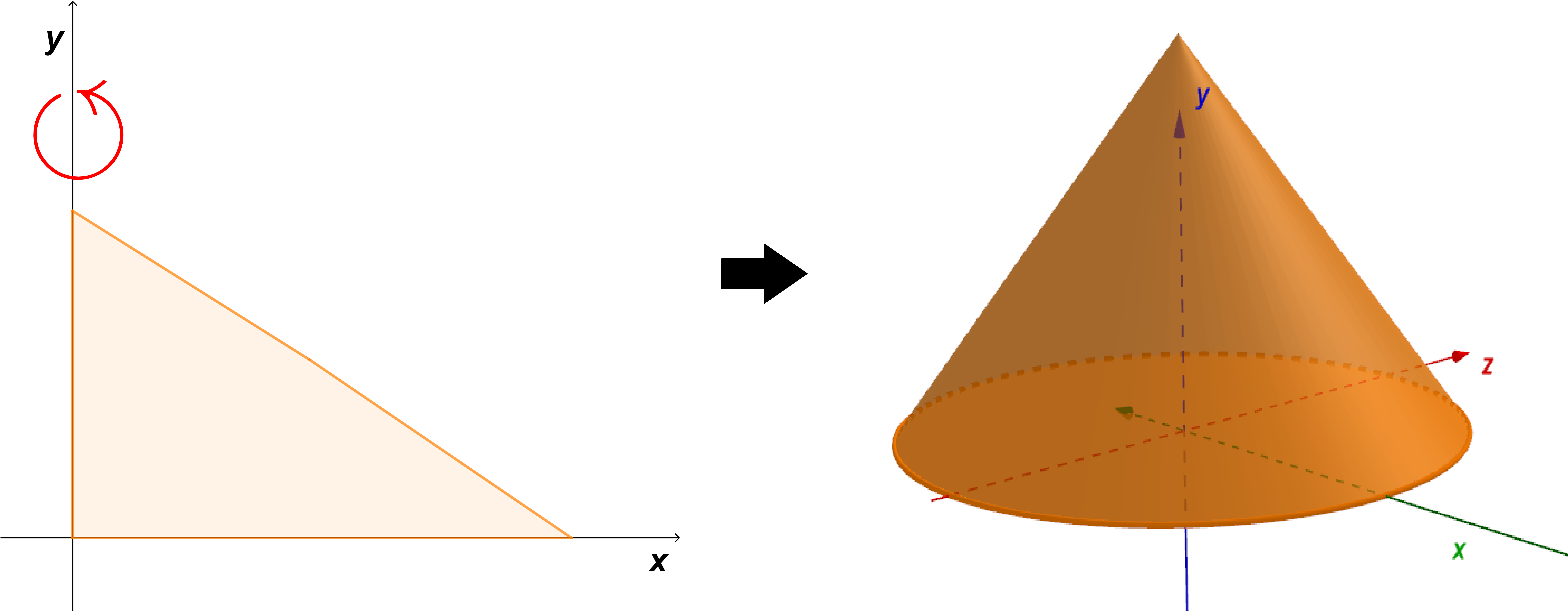
En la siguiente figura $(2)$ tenemos un triángulo rectángulo isósceles (figura de la izquierda), si nosotros hacemos girar este triángulo alrededor del eje $y$ lo que obtendremos es una pirámide como el lado derecho de la figura 2.

A estas figuras «creadas» se les conoce como superficies de revolución, a continuación veremos como calcular su volumen por el método de los discos.

Método de los discos

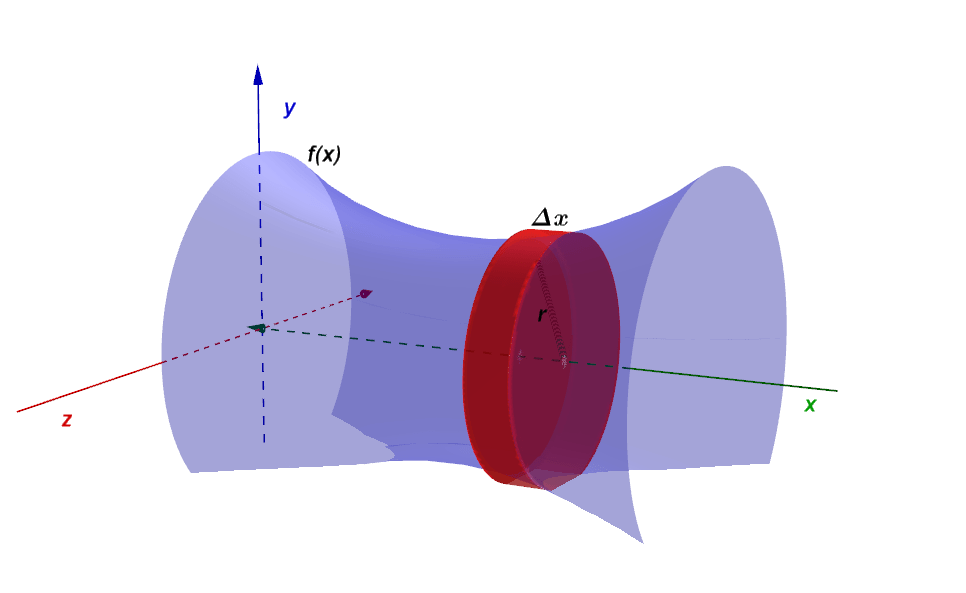
Supongamos que tenemos una función $f(x)$ en un intervalo $[a, b]$ y que cortamos una «rebanada» con un ancho $\Delta x$ de la función $f(x)$ como se muestra en la figura $(3)$.

Al hacer girar esta función alrededor del eje $x$ obtendremos una superficie de revolución (figura $(4)$), la «rebanada» que tomamos al girarlo alrededor del eje obtendremos un cilindro de radio $r$ y ancho $\Delta x$.

Para calcular el volumen de esta superficie de revolución la «rebanamos» $n$ veces y sumamos estos pedazos, es decir:

Volumen de la superficie de revolución $\approx \sum_{i=1}^{n}$ volúmenes de los cilindros

Recordemos que el volumen de un cilindro está dado como $V=\pi r^{2}h$, entonces el volumen de nuestra superficie de revolución es:

$$V \approx \sum_{i=1}^{n}\pi r^{2}\Delta x=\sum_{i=1}^{n}\pi [f(x)]^{2}\Delta x$$

Si tomamos el límite cuando $n \to \infty$ obtenemos:

$$V=\lim_{n \to \infty}\sum_{i=1}^{n}\pi [f(x)]^{2}\Delta x=\pi \int_{a}^{b}[f(x)]^{2}dx$$

Por lo que definimos el volumen de una superficie de revolución alrededor del eje $x$ como:

$$V=\int_{a}^{b} Área(x)dx=\pi \int_{a}^{b}[R(x)]^{2}dx \tag{1}$$

Análogamente, se puede deducir lo mismo para una superficie de revolución generado por una curva plana alrededor del eje $y$. Se define el volumen de una superficie de revolución alrededor del eje $y$ como:

$$V=\pi \int_{c}^{d}[R(y)]^{2}dy \tag{2}$$

Observación: Para el método de los discos el corte siempre debe ser perpendicular al eje de rotación.

Método de las arandelas

Si la región que se hace girar para generar el sólido de revolución no se acerca al eje de rotación, ni está en él, tendremos que al girarlo sobre el eje se obtendrá un agujero en su centro, es decir, un sólido de revolución con un agujero alrededor del eje de rotación. Si utilizamos el mismo método visto anteriormente para calcular su volumen, en vez de discos, tendremos que las secciones transversales perpendiculares al eje de rotación son arandelas, el área de la arandela está dada como:

$$A=\pi R^{2}(x)-\pi r^{2}(x)=\pi\left ( R^{2}(x)-r^{2}(x) \right )$$

Donde $R(x)$ es el radio mayor y $r(x)$ es el radio menor de la arandela como se muestra en la figura $(5)$, por lo que nos interesa el volumen entre $R(x)$ y $r(x)$.

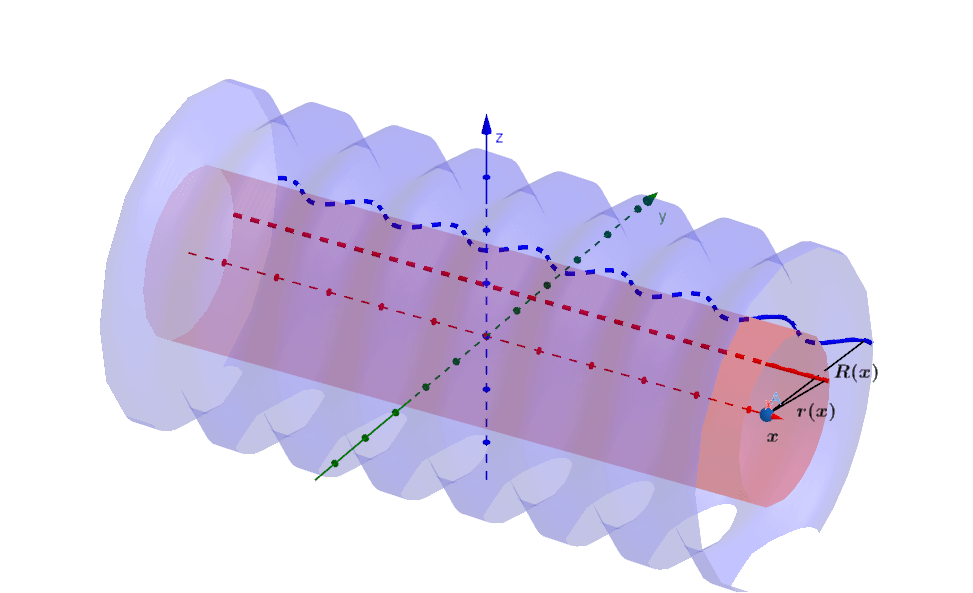
Por consecuencia, el volumen lo podemos calcular como:

$$V=\pi \int_{a}^{b} \left ( R^{2}(x)-r^{2}(x) \right )dx \tag{3}$$

Veamos un ejemplo.

Ejemplos

• Calcula el volumen del sólido de revolución formado al hacer girar la región acotada por la grafica $f(x)=\sqrt{\sin(x)}$, alrededor del eje $x$ y acotadas por las rectas $x=0$ y $x=\pi$.

En este caso obtenemos la siguiente figura $(6)$.

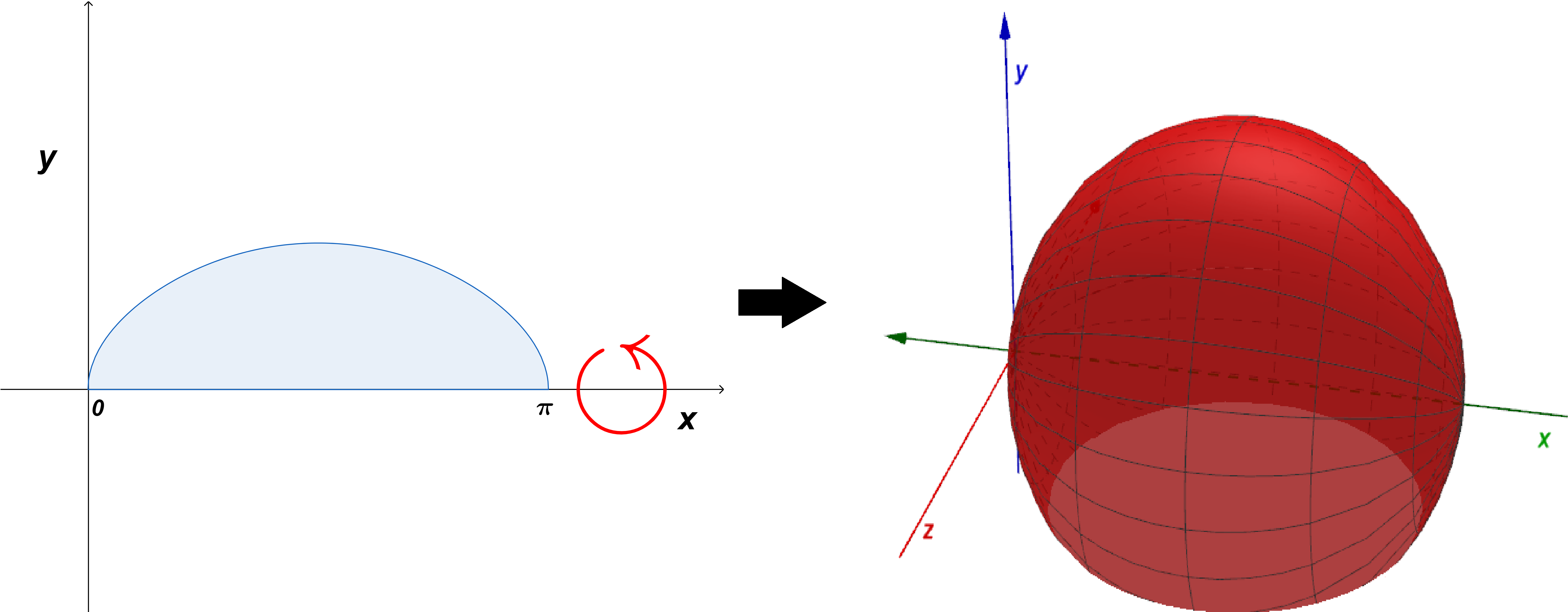
Utilizamos la relación $(1)$, ya que la función gira alrededor del eje $x$, por lo que el volumen de este sólido de revolución es:

$$V=\pi \int_{0}^{\pi}\left ( \sqrt{\sin(x)}\right )^{2}dx=\pi \int_{0}^{\pi}\sin(x)dx=\pi (-\cos(x))\bigg|_{0}^{\pi}=\pi -(-1-1)=2 \pi$$

• Determinar el volumen del sólido de revolución generado alrededor de $y=g(x)=1$ por la función $y=\sqrt{x}$ y las rectas $x=1$ y $x=4$ (figura $(7)$).

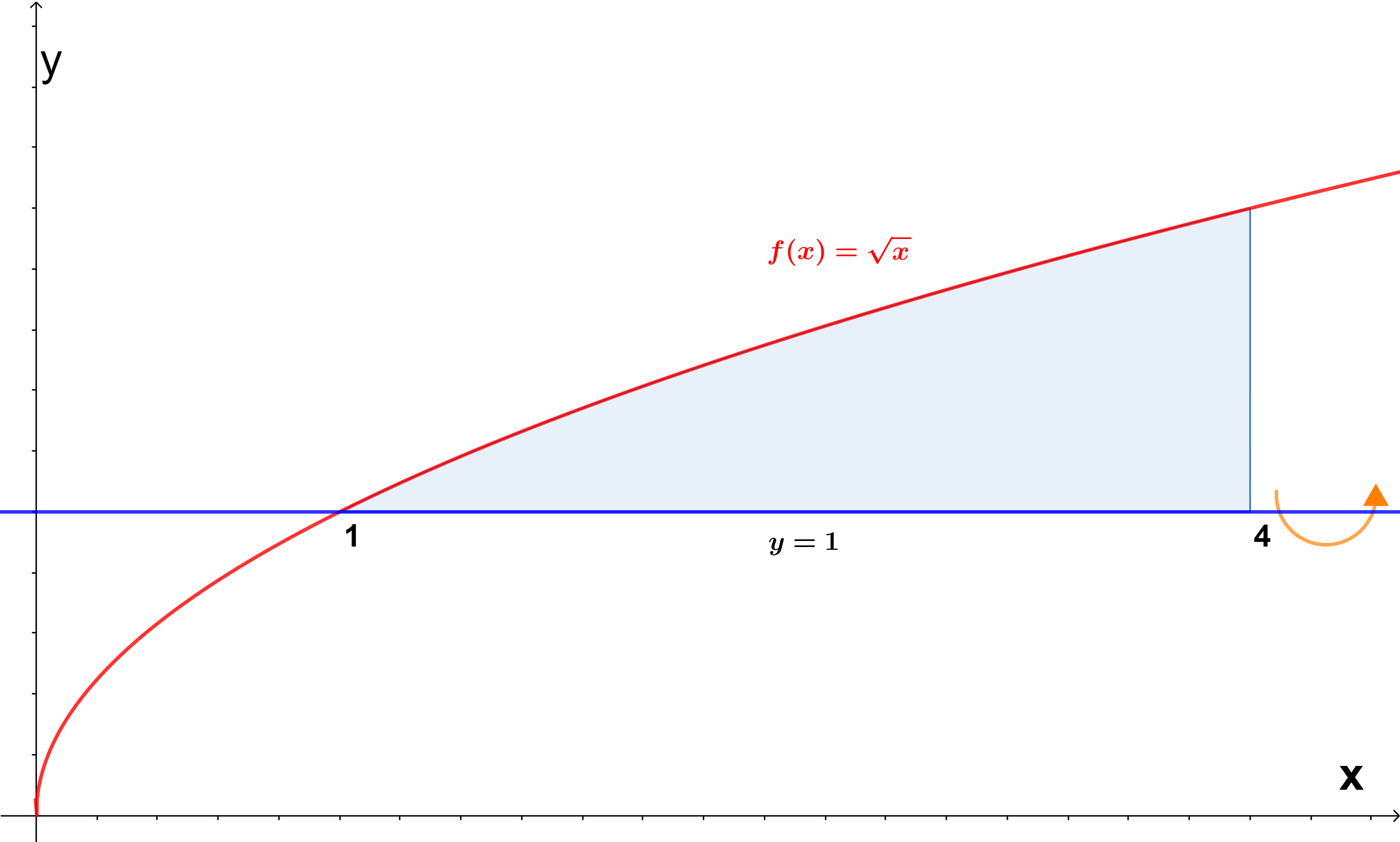
Al girar la función $f(x)=\sqrt{x}$ alrededor de $y=1$ tendremos una especie de parábola.

Observamos que:

$$R(x)=f(x)-g(x)=\sqrt{x}-1 \Rightarrow R^{2}(x)=x-2\sqrt{x}+1$$

Por ende, utilizamos la relación $(1)$ para calcular el volumen como:

$$V=\pi \int_{1}^{4} \left (x-2\sqrt{x}+1 \right )dx=\pi \left ( \frac{x^{2}}{2}-2\frac{2}{3}x^{3/2}+x \right )\bigg|_{1}^{4}=\frac{7\pi}{6}$$

• Determina el volumen del sólido de revolución acotada por las curvas $y=x^{2}+1$ y la recta $y=-x+3$ alrededor del eje $x$.

Para saber en qué intervalo vamos a integrar, igualamos las funciones:

$$x^{2}+1=-x+3 \Rightarrow x^{2}+x-2=0 \Rightarrow (x+2)(x-1)=0$$

Por lo que integramos desde $x=-2$ a $x=1$

Del eje de rotación, sea el radio menor $r(x)=x^{2}+1$ por estar más próximo a este eje en este intervalo, y sea el radio mayor $R(x)=-x+3$, como se muestra en la figura $(8)$.

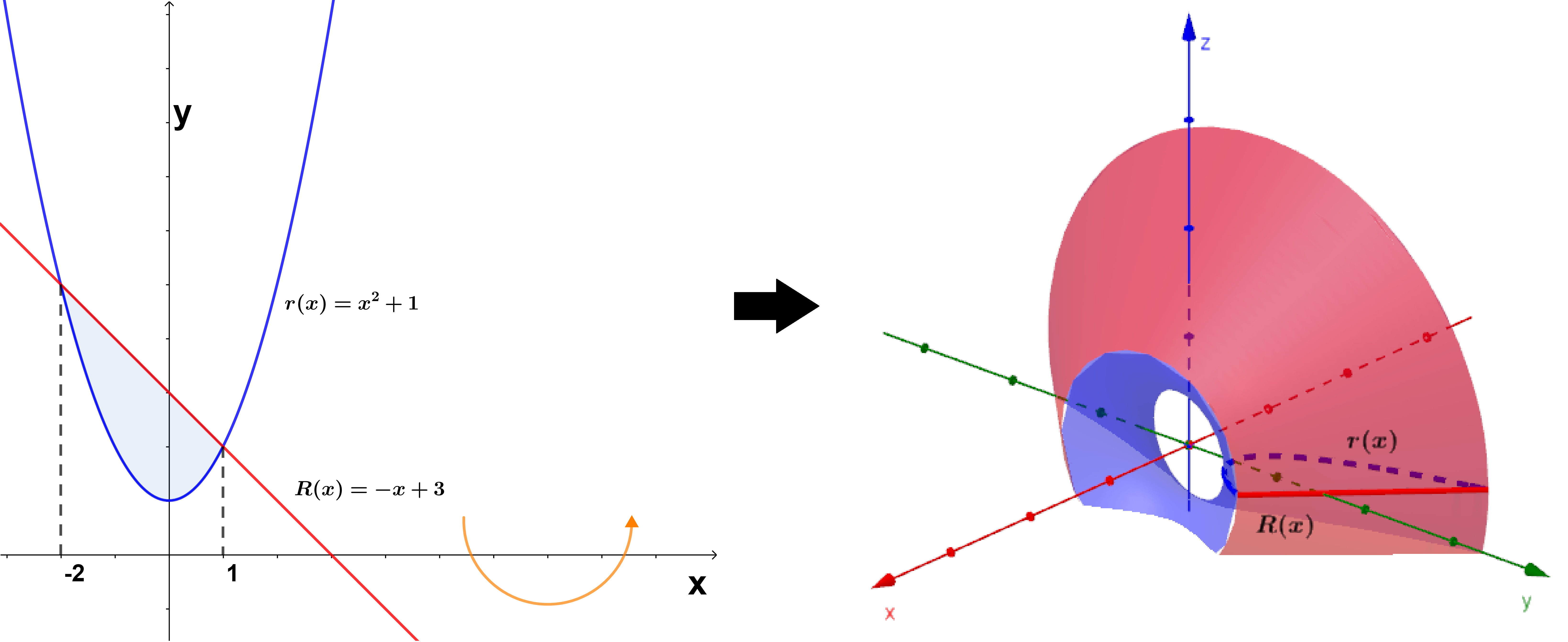
Para calcular el volumen de este sólido, utilizamos la relación $(3)$, por lo que:

$$V=\pi \int_{a}^{b} \left ( R^{2}(x)-r^{2}(x) \right )dx=\int_{-2}^{1}\pi \left [ \left ( -x+3 \right )^{2}-\left ( x^{2}+1 \right )^{2} \right ]dx$$

$$=\int_{-2}^{1}\pi \left ( 8-6x-x^{2}-x^{4} \right )dx=\pi \left [ 8x-3x^{2}-\frac{x^{3}}{3}-\frac{x^{5}}{5} \right ]\bigg|_{-2}^{1}=\frac{117\pi}{5}$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Determine el volumen del solido resultante al hacer girar la región comprendida entre el eje $y$ y la curva $x=2/y$, donde $1\leq y \leq 4$, alrededor del eje y.
2. Encuentre el volumen del solido generado al giran la región acotada por las graficas $y=\sqrt{x}$, $y=x^{2}$ en torno al eje x.
3. Encuentre el volumen del solido generado al giran la región acotada por las graficas $y=x^{2}+1$, $y=0$, $x=0$ y $x=1$ en torno al eje y.
4. La circunferencia $x^{2}+y^{2}=a^{2}$ se hace girar alrededor del eje y, calcular su volumen.
5. Un fabricante diseña un objeto en forma de esfera con un radio de 5 pulgadas y con un orificio cilíndrico en su interior. El hueco tiene un radio de 3 pulgadas ¿Cuál es el volumen del objeto resultante?

Más adelante…

En esta entrada deducimos las relaciones para calcular el volumen de un sólido generado por rotación alrededor de un eje por el método del disco y también deducimos la relación para calcular el volumen de un sólido generado por rotación entre dos curvas dadas por el método del anillo, en la siguiente entrada veremos otro método para calcular el volumen de un sólido generado llamado el método de las capas cilíndricas.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral II.
• Entrada anterior del curso: Cálculo Diferencial e Integral II: Longitud de arco – El blog de Leo (nekomath.com)
• Siguiente entrada del curso: Cálculo Diferencial e Integral II: Cálculo de volúmenes por medio de casquillos cilíndricos – El blog de Leo (nekomath.com)