Introducción
En esta entrada veremos una breve introducción a las interacciones básicas entre dos v.a.’s. En una entrada previa vimos cómo se interpretaban las operaciones con eventos, y después vimos algunos conceptos asociados a la interacción entre eventos, como es el caso de la definición de independencia. De manera similar, es razonable que definamos ciertos conceptos para describir el comportamiento probabilístico de dos variables aleatorias de manera conjunta.
Primero, un poco de notación
Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y sean $X\colon\Omega\to\RR$, $Y\colon\Omega\to\RR$ dos variables aleatorias. Aquí estamos siendo muy explícitos con el hecho de que el dominio de ambas v.a.’s debe de ser el mismo. Esto es importante porque los eventos que involucran a $X$ y a $Y$ deben de ser elementos del mismo σ-álgebra. Además, las operaciones entre v.a.’s están bien definidas siempre y cuando estas tengan el mismo dominio, pues se definen puntualmente.
Primero, demos un poco de notación. Sean $A$ y $B \in \mathscr{B}(\RR)$. Para denotar la probabilidad del evento en el que $X \in A$ y $Y \in B$ se sigue la siguiente notación:
\begin{align*} \Prob{X \in A, Y \in B} &= \Prob{(X \in A)\cap(Y \in B)}. \end{align*}
Es decir, $(X \in A, Y \in B)$ es la notación para expresar el evento $(X \in A) \cap (Y \in B)$. Observa que este conjunto sí es un evento, pues $X$ y $Y$ son v.a.’s, así que tanto $(X \in A)$ como $(Y \in B)$ son elementos de $\mathscr{F}$, así que también su intersección lo es.
De este modo, podemos expresar muchas probabilidades de intersecciones de eventos de forma más compacta. Por ejemplo:
\begin{align*} \Prob{X = x, Y = y} &= \Prob{(X = x) \cap (Y = y)}, \\[1em] \Prob{X \leq x, Y \leq y} &= \Prob{(X \leq x) \cap (Y \leq y)}, \end{align*}
etcétera.
Independencia de variables aleatorias
En la Unidad 1 de este curso hablamos sobre la independencia de eventos. El paso que sigue ahora es definir la noción de independencia de variables aleatorias. De manera similar a los eventos, que $X$ y $Y$ sean variables aleatorias independientes significa que un evento que involucra a $X$ no afecta las probabilidades de $Y$. Por ello, la noción de independencia se dará en términos de eventos.
Definición 1. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y sean $X\colon\Omega\to\RR$ y $Y\colon\Omega\to\RR$ variables aleatorias. Diremos que $X$ y $Y$ son independientes si y sólamente si para todo $A$, $B \in \mathscr{B}(\RR)$ se cumple
\begin{align*} \Prob{X \in A, X \in B} &= \Prob{X \in A} \Prob{X \in B}. \end{align*}
También es posible caracterizar la independencia de v.a.’s mediante sus funciones de distribución. Para ello, es necesario definir el concepto de función de distribución conjunta de dos v.a.’s. Esta se define como sigue:
Definición 2. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y sean $X\colon\Omega\to\RR$ y $Y\colon\Omega\to\RR$ variables aleatorias. Se define la función de distribución conjunta de $X$ y $Y$, $F_{X,Y}\colon\RR^{2}\to\RR$, como sigue:
\begin{align*} F_{X,Y}(x,y) &= \Prob{X \leq x, Y \leq y}, & \text{para cada $(x,y) \in \RR^{2}$}. \end{align*}
Esta es una «generalización» multidimensional de la función de distribución de una variable aleatoria. Es decir, sabemos que \(\Prob{X \leq x}\) es la probabilidad de que la v.a. \(X\) tome un valor dentro del intervalo \((-\infty, x]\). De manera similar, \(\Prob{X \leq x, Y \leq y}\) es la probabilidad de que las v.a.’s \(X\) y \(Y\) tomen un valor dentro del intervalo \((-\infty, x]\) y \((-\infty, y]\), respectivamente. Esto es, si pensamos a \((X, Y)\) como un punto aleatorio en \(\RR^{2}\), entonces \(\Prob{X \leq x, Y \leq y}\) es la probabilidad de que \((X,Y)\) sea un punto dentro del rectángulo \((-\infty, x] \times (-\infty, y]\).
El siguiente teorema nos brinda un criterio de independencia más sencillo que el de la Definición 1:
Teorema 1. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y sean $X\colon\Omega\to\RR$ y $Y\colon\Omega\to\RR$ variables aleatorias. Las siguientes proposiciones son equivalentes:
- $X$ y $Y$ son independientes.
- Para cualesquiera $x$, $y \in \RR$ se cumple \begin{align*} F_{XY}(x,y) &= F_{X}(x) F_{Y}(y). \end{align*}
Demostrar que 1. implica a 2. no es complicado, y lo dejamos como tarea moral. Por otro lado, demostrar 2. implica a 1. rebasa los contenidos de este curso, por lo que omitiremos esta parte de la demostración.
Este teorema hace más sencillo verificar si dos v.a.’s son independientes o no lo son. Primero, porque el trabajo se reduce a trabajar con las funciones de distribución. Además, a continuación veremos que es posible recuperar las funciones de probabilidad (masa y densidad) a partir de las funciones de probabilidad conjunta. Por ello, podremos verificar si dos v.a.’s son independientes comparando su distribución conjunta con el producto de sus distribuciones univariadas, gracias al Teorema 1.
Funciones de probabilidad conjunta para v.a.’s discretas
Al haber definido la función de distribución conjunta, se desprenden dos casos importantes: el caso discreto y el caso continuo. En el caso en el que $X$ y $Y$ son v.a.’s discretas, es posible definir la función de masa de probabilidad conjunta de $X$ y $Y$. Esta se define como sigue.
Definición 3. Sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad y sean $X\colon\Omega\to\RR$ y $Y\colon\Omega\to\RR$ v.a.’s discretas. Se define la función de masa de probabilidad conjunta de $X$ y $Y$, $p_{X,Y}\colon\RR^{2}\to\RR$ como sigue:
\begin{align*} p_{X,Y}(x, y) &= \Prob{X = x, Y = y}, & \text{para cada $(x,y) \in \RR^{2}$}. \end{align*}
Es decir, el valor $p_{X,Y}(x,y)$ es la probabilidad de que $X$ tome el valor $x$ y $Y$ tome el valor $y$. Ahora, antes de seguir, es recomendable que recuerdes el teorema de probabilidad total que vimos en una entrada previa. Sabemos que $Y[\Omega]$ es un conjunto a lo más infinito numerable, pues $Y$ es una v.a. discreta. Por ello, podemos ver a $Y[\Omega]$ como una unión numerable de conjuntos, donde cada uno de estos conjuntos tiene un único elemento. Es decir, tomamos los conjuntos $\{y\}$, para cada $y \in Y[\Omega]$, y los unimos a todos:
\begin{align*} Y[\Omega] &= \bigcup_{y \in Y[\Omega]} \{ y \}. \end{align*}
De este modo,
\begin{align*} Y^{-1}[Y[\Omega]] &= Y^{-1}{\left[\bigcup_{y \in Y[\Omega]} \{ y \} \right]} \\[1em] &= \bigcup_{y \in Y[\Omega]} Y^{-1}{\left[ \{ y \} \right]} \\[1em] &= \bigcup_{y \in Y[\Omega]} (Y = y). \tag{$\triangle$} \end{align*}
Observa que esta es una unión de conjuntos ajenos, pues para cada $y_{1}$, $y_{2} \in Y[\Omega]$ se cumple que si $y_{1} \neq y_{2}$, entonces $\{ y_{1} \} \cap \{ y_{2} \} = \emptyset$. Además,
\begin{align*} Y^{-1}[ \{ y_{1} \} \cap \{ y_{2} \} ] &= Y^{-1}[ \{ y_{1} \}] \cap Y^{-1}[\{ y_{2} \} ], \tag{$*$} \\[1em] Y^{-1}[ { y_{1} } \cap { y_{2} } ] &= Y^{-1}[\emptyset] = \emptyset, \tag{$**$}\end{align*}
así que por $(*)$ y $(**)$ podemos concluir que $Y^{-1}[\{ y_{1} ] \cap Y^{-1}[ \{ y_{2} \} ] = \emptyset$. Por lo tanto, la unión
\begin{align*} \bigcup_{y \in Y[\Omega]} (Y = y) \end{align*}
es una unión de eventos ajenos. Además, por propiedades de la imagen inversa, sabemos que
\begin{align*} \Omega \subseteq Y^{-1}[Y[\Omega]]. \end{align*}
Por otro lado, como el dominio de $Y$ es $\Omega$, también sabemos que $Y^{-1}[Y[\Omega]] \subseteq \Omega$, así que $\Omega = Y^{-1}[Y[\Omega]]$. Finalmente, por $(\triangle)$ se tiene que
\begin{align*} \Omega &= \bigcup_{y \in Y[\Omega]} (Y = y). \end{align*}
Es decir, $\{ \, (Y = y) \mid y \in Y[\Omega] \,\}$ forma una partición de $\Omega$. Sea $x \in X[\Omega]$. Como lo anterior nos da una partición de $\Omega$, podemos aplicar el teorema de probabilidad total para obtener que
\begin{align*} \Prob{X = x} &= \sum_{y \in Y[\Omega]} \Prob{X = x, Y = y}. \end{align*}
Análogamente, para cada $y \in Y[\Omega]$ se tiene que
\begin{align*} \Prob{Y = y} &= \sum_{x \in X[\Omega]} \Prob{X = x, Y = y}. \end{align*}
En términos de las funciones de masa de probabilidad, lo anterior quiere decir que podemos recuperar la masa de probabilidad de $X$ y de $Y$ a partir de la función de masa de probabilidad conjunta, como sigue:
\begin{align*} p_{X}(x) &= \sum_{y \in Y[\Omega]} p_{X,Y}(x, y) & \text{para cada $x \in X[\Omega]$}, \\[1em] p_{Y}(y) &= \sum_{x \in X[\Omega]} p_{X,Y}(x, y) & \text{para cada $y \in Y[\Omega]$}. \end{align*}
Este procedimiento de obtener la función de masa de probabilidad de una v.a. a partir de la masa de probabilidad conjunta se conoce como marginalización, y las funciones resultantes son conocidas como las funciones de masa de probabilidad marginales.
Ejemplo 1. Sean $X$ y $Y$ dos v.a.’s discretas con función de masa de probabilidad conjunta $p_{X,Y}\colon\RR^{2}\to\RR$ dada por:
\begin{align*} p_{X,Y} &= \begin{cases} 0.05 & \text{si $(x, y) = (0,3)$ o $(x,y) = (1,1)$ o $(x, y) = (2,4)$}, \\[1em] 0.1 & \text{si $(x,y)=(0,2)$ o $(x,y) = (1,3)$ o $(x,y) = (2,1)$}, \\[1em] 0.15 & \text{si $(x,y) = (2,2)$}, \\[1em] 0.2 & \text{si $(x,y) = (0,1)$ o $(x,y) = (1,4)$}, \\[1em] 0 & \text{en otro caso}. \end{cases} \end{align*}
Una buena manera de organizar la información contenida en esta función es mediante una tabla como la siguiente:
| Valores posibles de $X$ | ||||
| 0 | 1 | 2 | ||
| Valores posibles de $Y$ | 1 | 0.2 | 0.05 | 0.1 |
| 2 | 0.1 | 0 | 0.15 | |
| 3 | 0.05 | 0.1 | 0 | |
| 4 | 0 | 0.2 | 0.05 | |
De este modo, $\Prob{X = 0, Y = 1} = 0.2$, y $\Prob{X=0, Y =3} = 0.05$. A partir de las probabilidades de la tabla podemos calcular la función de masa de probabilidad de $X$, $p_{X}\colon\RR\to\RR$. Para ello, simplemente debemos de marginalizar sobre cada uno de los valores que toma $X$. De este modo, obtenemos que
\begin{align*} p_{X}(0) &= p_{X,Y}(0,1) + p_{X,Y}(0,2) + p_{X,Y}(0,3) + p_{X,Y}(0,4) = 0.2 + 0.1 + 0.05 + 0 = 0.35, \\[1em] p_{X}(1) &= p_{X,Y}(1,1) + p_{X,Y}(1,2) + p_{X,Y}(1,3) + p_{X,Y}(1,4) = 0.05 + 0 + 0.1 + 0.2 = 0.35, \\[1em] p_{X}(2) &= p_{X,Y}(2,1) + p_{X,Y}(2,2) + p_{X,Y}(2,3) + p_{X,Y}(2,4) = 0.1 + 0.15 + 0 + 0.05 = 0.3, \end{align*}
por lo que la función de masa de probabilidad de $X$ nos queda
\begin{align*} p_{X}(x) &= \begin{cases} 0.35 & \text{si $x = 0$ o $x = 1$}, \\[1em] 0.3 & \text{si $x = 2$}. \end{cases} \end{align*}
Sin embargo, observa que el uso de una tabla sólo tiene sentido si $X[\Omega]$ y $Y[\Omega]$ son conjuntos finitos. De otro modo, sería una «tabla» infinita, y nunca acabaríamos de escribirla…
Independencia en el caso discreto
Una consecuencia (casi inmediata) del Teorema 1 es el siguiente criterio de independencia para v.a.’s discretas.
Proposición 1. Sean \(X\), \(Y\) variables aleatorias. Si \(X\) y \(Y\) son discretas, entonces \(X\) y \(Y\) son independientes si y sólamente si
\begin{align*} \Prob{X = x, Y = y} &= \Prob{X = x} \Prob{Y = y}, & \text{para cualesquiera \(x,y \in \RR\).} \end{align*}
Por ejemplo, retomemos las v.a.’s del Ejemplo 1. Sumando los valores en el renglón donde \(Y = 1\), obtenemos que
\begin{align*} \Prob{Y = 1} = 0.35, \end{align*}
y nosotros calculamos que \(\Prob{X = 1} = 0.35\). En consecuencia,
\begin{align} \label{eq:prod} \Prob{X = 1}\Prob{Y = 1} &= 0.1225.\end{align}
Sin embargo, de acuerdo con la tabla, \(\Prob{X = 1, Y = 1} = 0.05\), que no coincide con el valor en \eqref{eq:prod}. Por ello, podemos concluir que las v.a.’s del Ejemplo 1 no son independientes.
Función de densidad conjunta para v.a.’s continuas
Como de costumbre, el caso para las v.a.’s continuas es distinto. En este caso, lo que tendremos es una función de densidad conjunta, que juega el mismo papel que una función de densidad univariada, pero para \(2\) v.a.’s conjuntamente. Esto da lugar a la siguiente definición.
Definición. Sean \(X\) y \(Y\) v.a.’s continuas, y \(F_{X,Y}\colon\RR^{2}\to\RR\) su función de distribución conjunta. Entonces \(F_{X,Y}\) puede expresarse como sigue:
\begin{align*} F_{X,Y}(x,y) &= \int_{-\infty}^{x}\int_{-\infty}^{y} f_{X,Y}(u,v) \, \mathrm{d}v \, \mathrm{d}u, & \text{para cada \((x, y) \in \RR^{2}\).} \end{align*}
De este modo, \(f_{X,Y}\colon\RR^{2}\to\RR\) es llamada la función de densidad conjunta de \(X\) y \(Y\).
De igual forma que con las función de distribución conjunta, la función de densidad conjunta es una generalización multivariada de la función de densidad. Además, también existen técnicas de marginalización que son análogas al caso discreto. Primero, recuerda que integrar la función de densidad sobre un intervalo es nuestra forma de sumar continuamente las probabilidades de cada punto en el intervalo. Esto es:
\begin{align*} \Prob{X \in (a,b]} &= \int_{a}^{b} f_{X}(x) \, \mathrm{d}x. \end{align*}
Si tomamos la idea del teorema de probabilidad total, pero integramos sobre todo el conjunto de valores de una de las v.a.’s (en vez de sumar, como hicimos en el caso discreto), podemos expresar la función de densidad marginal de \(X\) como
\begin{align*} f_{X}(x) &= \int_{-\infty}^{\infty} f_{X,Y}(x, y) \, \mathrm{d}y, & \text{para cada \(x\in\RR\).}\end{align*}
Es decir, integramos sobre todo el dominio de la v.a. que queremos quitar, que en este caso es \(Y\). Análogamente, para \(Y\) se tiene que
\begin{align*} f_{Y}(y) &= \int_{-\infty}^{\infty} f_{X,Y}(x, y) \, \mathrm{d}x, & \text{para cada \(y\in\RR\).}\end{align*}
Este es el proceso de marginalización para el caso continuo. Observa que las funciones resultantes son las funciones de densidad marginales. Como tal, los valores que toman estas funciones no son probabilidades, por lo que la marginalización es más sutil que en el caso discreto (ya que el teorema de probabilidad total se usa para probabilidades, y para particiones a lo más numerables).
Ejemplo 2. Sean \(X\) y \(Y\) dos v.a.’s tales que su función de densidad conjunta es \(f_{X,Y}\) dada por
\begin{align*} f_{X,Y}(x,y) &= \begin{cases} y{\left( \dfrac{1}{2} − x\right)} + x &\text{si \(x \in (0,1)\) y \(y \in (0,2)\),} \\[1em] 0 & \text{en otro caso.}\end{cases}\end{align*}
La gráfica de esta función se ve como sigue:
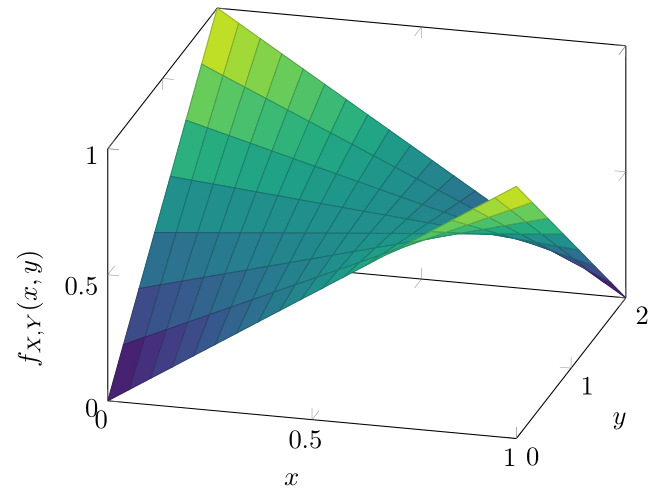
Sin embargo, hay un detallito que quizás tengas en la cabeza: ¿cómo se interpreta que esta función sea «de densidad», en un sentido vibariado? A grandes rasgos, debe de cumplir lo mismo que una función de densidad univariada. En particular, el valor de la integral sobre su dominio debe de ser \(1\). En este caso, esto significa que se debe de cumplir que
\begin{align*} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f_{X,Y}(x,y) \, \mathrm{d}x \, \mathrm{d}y &= 1. \end{align*}
Como muy probablemente no conoces métodos (ni teoría) de integración bivariada, simplemente te diremos que \(f_{X,Y}\) sí es una función de densidad bivariada, y que sí cumple la condición anterior.
Por otro lado, algo que sí podemos hacer con los conocimientos que posees hasta ahora es obtener las marginales. Obtengamos la densidad marginal de \(X\), para lo cual hay que integrar \(f_{X,Y}\) sobre todo el dominio de \(Y\):
\begin{align*} \int_{-\infty}^{\infty} f_{X,Y}(x,y) \, \mathrm{d}y &= \int_{0}^{2} {\left[ y{\left( \dfrac{1}{2} − x\right)} + x \right]} \, \mathrm{d}y, \end{align*}
en donde \(x \in (0,1)\), pues es donde la densidad conjunta no vale \(0\). Como esta integral es con respecto a \(y\), podemos pensar que \(x\) es una constante respecto a la variable de integración. Por ello, la integral anterior puede resolverse de manera directa con herramientas de Cálculo II:
\begin{align*} \int_{0}^{2} {\left[ y{\left( \dfrac{1}{2} − x\right)} + x \right]} \, \mathrm{d}y &= \int_{0}^{2} {\left( \dfrac{1}{2} − x\right)}y \, \mathrm{d}y + \int_{0}^{2} x \mathrm{d}y \\[1em] &= {\left( \dfrac{1}{2} − x\right)} \int_{0}^{2} y \, \mathrm{d}y + x \int_{0}^{2} 1 \, \mathrm{d}y \\[1em] &= {\left(\frac{1}{2} − x\right)}{\left( \frac{y^{2}}{2} \right)}\Bigg|_{y=0}^{2} + x(2 − 0) \\[1em] &= {\left(\frac{1}{2} − x\right)} {\left( \frac{4 − 0}{2} \right)} + 2x \\[1em] &= 2{\left( \frac{1}{2} − x \right)} + 2x \\[1em] &= 1 + 2x − 2x \\[1em] &= 1, \end{align*}
para cada \(x \in (0,1)\). En consecuencia, la densidad marginal de \(X\) es \(f_{X}\) dada por
\begin{align*} f_{X}(x) &= \begin{cases} 1 & \text{si \(x \in (0,1)\),} \\[1em] 0 & \text{en otro caso.} \end{cases} \end{align*}
Así, llegamos a que \(X\) sigue una distribución uniforme en el intervalo \((0,1)\).
Independencia en el caso continuo
De manera similar al caso discreto, además del criterio dado por el Teorema 1, podemos dar la siguiente criterio de independencia para dos v.a.’s continuas.
Proposición 2. Sean \(X\), \(Y\) variables aleatorias. Si \(X\) y \(Y\) son continuas, entonces \(X\) y \(Y\) son independientes si y sólamente si
\begin{align*} f_{X,Y}(x,y) &= f_{X}(x) f_{Y}(y), & \text{para cualesquiera \(x,y \in \RR\),} \end{align*}
donde \(f_{X,Y}\) es la función de densidad conjunta de \(X\) y \(Y\), y \(f_{X}\) y \(f_{Y}\) son las funciones de densidad marginales.
Es decir, dos v.a.’s continuas son independientes si su función de densidad conjunta es el producto de sus funciones de densidad (marginales).
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.
- Demuestra que 1. implica a 2. en el Teorema 1.
- En el Ejemplo 1:
- Verifica que la función $p_{X}\colon\RR\to\RR$ que obtuvimos es una función de masa de probabilidad.
- Encuentra $p_{Y}\colon\RR\to\RR$, la función de masa de probabilidad de $Y$.
- En el Ejemplo 2:
- Encuentra la función de densidad marginal de \(Y\).
- ¿Son independientes \(X\) y \(Y\)?
Más adelante…
Usaremos los temas que vimos en esta entrada en la próxima entrada, ya que serán necesarios algunos detallitos de probabilidad multivariada para entender las propiedades del valor esperado que veremos a continuación. Por el momento sólo es importante que sepas que existen estos temas de probabilidad multivariada, y entiendas lo que significan los conceptos vistos en esta entrada.
En un curso de Probabilidad II verás con muchísimo detalle los temas que presentamos en esta entrada, así que no te preocupes si los temas que vimos aquí no te quedaron completamente claros.
Entradas relacionadas
- Ir a Probabilidad I
- Entrada anterior del curso: Propiedades del Valor Esperado
- Siguiente entrada del curso: Más Propiedades del Valor Esperado
