Introducción
En esta sección veremos unas funciones cuyas definiciones se basan en la función exponencial, a estas funciones se les conoce como funciones hiperbólicas, el nombre de hipérbolas se basa en que estas funciones cumplen la relación con la hipérbola:
$$x^{2}-y^{2}=1 \tag{1}$$
Funciones hiperbólicas
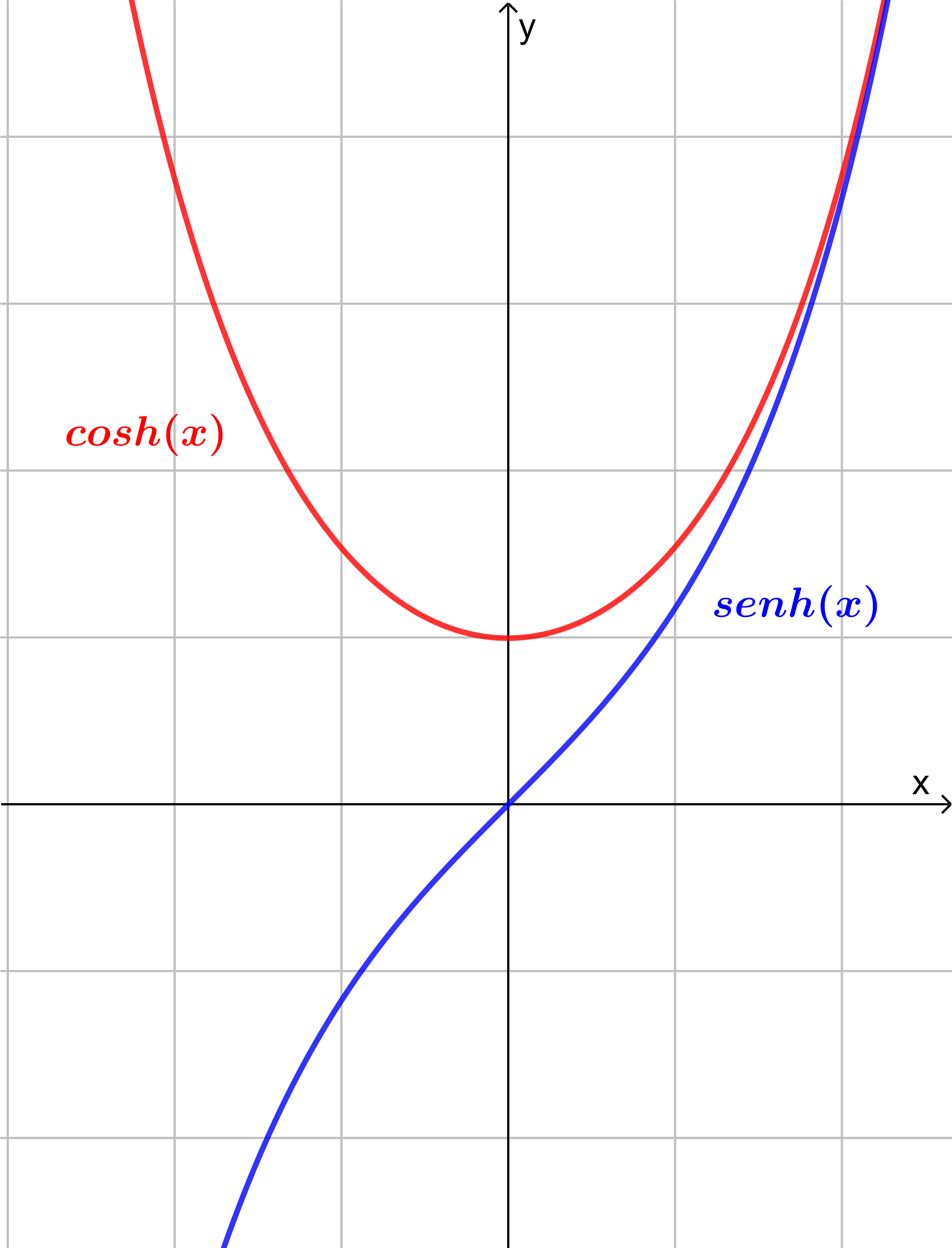
Recordemos que la relación $(1)$ es la ecuación de una hipérbola equilátera, por lo cual las asíntotas son perpendiculares. Definimos las funciones de seno hiperbólico y coseno hiperbólico como:
$$\sinh(x)=\frac{e^{x}-e^{-x}}{2} \tag{2}$$
$$\cosh(x)=\frac{e^{x}+e^{-x}}{2} \tag{3}$$
De estas dos funciones podemos definir las siguientes funciones:
$$\tanh(x)=\frac{\sinh(x)}{\cosh(x)}$$
$$\coth(x)=\frac{\cosh(x)}{\sinh(x)}$$
$$sech(x)=\frac{1}{\cosh(x)}$$
$$csch(x)=\frac{1}{\sinh(x)}$$
Notemos que estas funciones hiperbólicas llevan el nombre de las funciones trigonométricas y es que estas funciones trigonométricas tienen características similares a las funciones trigonométricas.
Veamos que las funciones hiperbólicas $\sinh(x)$ y $\cosh(x)$ cumplen la relación de una hiperbóla dada por la relación $(1)$:
$$\cosh^{2}(x)-\sinh^{2}(x)=\left ( \frac{e^{x}+e^{-x}}{2} \right )^{2}-\left ( \frac{e^{x}-e^{-x}}{2} \right )^{2}$$
$$=\frac{e^{2x}+2e^{x}e^{-x}+e^{-2x}}{4}+\frac{-e^{2x}+2e^{x}e^{-x}-e^{-2x}}{4}=\frac{2+2}{4}=1$$
$\space$
La función seno hiperbólico también cumple con ser una función impar, veamos:
$$\sinh(-x)=\frac{e^{-x}-e^{-(-x)}}{2}=\frac{e^{-x}-e^{x}}{2}=-\frac{e^{x}-e^{-x}}{2}=-\sinh(x)$$
Análogamente, se puede demostrar que las siguientes funciones son funciones impares: $\coth(x)$ y $csch(x)$, y las siguientes funciones son pares: $\cosh(x)$, $\tanh(x)$ y $sech(x)$.
Algunas relaciones importantes de estas funciones son las siguientes:
- $$e^{x}=\cosh(x)+\sinh(x)$$
- $$e^{-x}=\cosh(x)-\sinh(x)$$
Es fácil demostrar las relaciones anteriores por definición $(2)$ y $(3)$.
Otra propiedad es la siguiente:
- $$\sinh(x\pm y)=\sinh(x)\cosh(y)\pm \cosh(x)\sinh(y)$$
Demostración:
Por definición, tenemos que:
$$\sinh(x\pm y)=\frac{e^{x\pm y}-e^{-x\mp y}}{2}=\frac{e^{x}e^{\pm y}-e^{-x}e^{\mp y}}{2}$$
Por las relaciones anteriores se tiene que:
$$\frac{e^{x}e^{\pm y}-e^{-x}e^{\mp y}}{2} =\frac{(\cosh(x)+\sinh(x))(\cosh( y)\pm \sinh(y))-(\cosh(x)-\sinh(x))(\cosh(y)\mp \sinh(y))}{2}=$$
$$\frac{\cosh(x)\cosh(y)\pm \cosh(x)\sinh(y)+\sinh(x)\cosh(y)\pm \sinh(x)\sinh(y)-\cosh(x)\cosh(y)\pm \cosh(x)\sinh( y)}{2}$$
$$\frac{+(\sinh(x)\cosh(y)\mp \sinh(x)\sinh( y)}{2}$$
Dependiendo del signo, lo podemos reescribir como:
$$=\frac{2\sinh(x)\cosh( y)\pm 2\cosh(x)\sinh(y)}{2}=\sinh(x)\cosh(y)\pm \cosh(x)\sinh( y)$$
$\square$
La propiedad para la función $\cosh(x)$ viene dada como:
- $$\cosh(x\pm y)=\cosh(x)\cosh(x)\pm \sinh(x)\sinh(x)$$
De las relaciones anteriores se puede demostrar que:
- $$\cosh(2x)=\cosh^{2}(x)+\sinh^{2}(x)$$
- $$sinh(2x)=2\cosh(x)+\sinh(x)$$
La derivación e integración de estas funciones es sencillo, veamos la siguiente tabla:
| $$\frac{d}{dx}\sinh(x)=\cosh(x)$$ |
| $$\frac{d}{dx}\cosh(x)=\sinh(x)$$ |
| $$\frac{d}{dx}\tanh(x)=sech(x)$$ |
| $$\frac{d}{dx}\coth(x)=csch(x)$$ |
| $$\frac{d}{dx}sech(x)=-sech(x)\tanh(x)$$ |
| $$\frac{d}{dx}csch(x)=-csch(x)\coth(x)$$ |
Notemos que las derivadas son similares a las derivadas de las funciones trigonométricas, al ser la derivada una función inversa de la integral entonces las integrales son similares a las funciones trigonométricas, veamos la siguiente tabla:
| $$\int \sinh(x)=\cosh(x)+c$$ |
| $$\int \cosh(x)=\sinh(x)+c$$ |
| $$\int \tanh(x)=log(\cosh(x))+c$$ |
| $$\int \coth(x)=log(\sinh(x))+c$$ |
| $$\int sech(x)=2\tan^{-1}\left ( \tanh(\frac{x}{2}) \right )+c$$ |
| $$\int csch(x)=log\left ( \tanh(\frac{x}{2}) \right )$$ |
Funciones hiperbólicas inversas
Análogamente a las funciones trigonométricas, se definen las funciones hiperbólicas inversas como:
- $$\sinh^{-1}(x)=arcsinh(x)=ln\left ( x+\sqrt{x^{2}+1} \right )$$
- $$\cosh^{-1}(x)=arccosh(x)=ln\left ( x+\sqrt{x^{2}-1} \right )$$
- $$\tanh^{-1}(x)=arctanh(x)=\frac{1}{2}ln\left ( \frac{1+x}{1-x} \right )$$
- $$\coth^{-1}(x)=arccoth(x)=\frac{1}{2}ln\left ( \frac{x+1}{x-1} \right )$$
- $$sech^{-1}(x)=arcsech(x)=ln\left ( \frac{1+\sqrt{1-x^{2}}}{x} \right )$$
- $$csch^{-1}(x)=arccsch(x)=ln\left ( \frac{1}{x}+\sqrt{\frac{1}{x^{2}}+1} \right )$$
La demostración para la función hiperbólica inversa den $\sinh(x)$ es como sigue:
Sea $y=arcsinh(x) \Rightarrow \sinh(y)=x$
Utilizamos la relación $(1)$, por lo que:
$$\cosh^{2}(y)=1+\sinh^{2}(y)=1+x^{2}$$
$$\Rightarrow \cosh(y)=\sqrt{1+x^{2}}$$
Sumando en ambos lados de la igualdad para obtener la exponencial, se tiene que:
$$e^{y}=\cosh(y)+\sinh(y)=\sqrt{1+x^{2}}+x$$
$$y=arcsinh(x)=ln\left ( \sqrt{1+x^{2}}+x \right )$$
$\square$
La idea para las demostrar las demás funciones hiperbólicas inversas es la misma.
Tarea moral
Los siguientes ejercicios no son para evaluación pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionado con el tema visto.
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Demuestre la siguiente identidad: $\tanh^{2}(x)+sech^{2}(x)=1$.
- Demuestre que la función hiperbólica $\cosh(x)$ es una función impar.
- Demuestre que $\cosh(x\pm y)=\cosh(x)\cosh(x)\pm \sinh(x)\sinh(x)$.
- Demuestre que $\frac{d}{dx}csch(x)=-csch(x)\coth(x)$.
- Demuestre que $\int \tanh(x)=log(\cosh(x))+c$.
Más adelante…
En esta sección vimos las funciones hiperbólicas que cumplen con la ecuación de una hipérbola equilátera, así como, algunas propiedades tales como sus derivadas e integrales, también vimos que algunas de las propiedades de estas funciones son similares a las funciones trigonométricas, en la siguiente sección veremos una introducción a varias variables.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencial e Integral II: Longitud de arco en coordenadas polares – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencial e Integral II: Introducción a funciones de varias variables – El blog de Leo (nekomath.com)