Introducción

En la entrada anterior aprendimos a calcular el volumen de un sólido generado por rotación alrededor de un eje a través del método de los discos y el método de las arandelas, en esta entrada ahora veremos como calcular el volumen de un sólido por el método de casquillos cilíndricos o capas cilíndricas.

Método de casquillos cilíndricos o capas cilíndricas

Supongamos que tenemos una curva dada por $f(x)$ en un intervalo $[a.b]$, dividiendo este intervalo en subintervalos $[x_{i-1}, x_{i}]$ y para aproximarse a esta curva lo aproximamos por un polígono a una distancia $r_{1}$ y $r_{2}$ del eje $y$ y ancho $\Delta x$ como se muestra en la figura $(1)$.

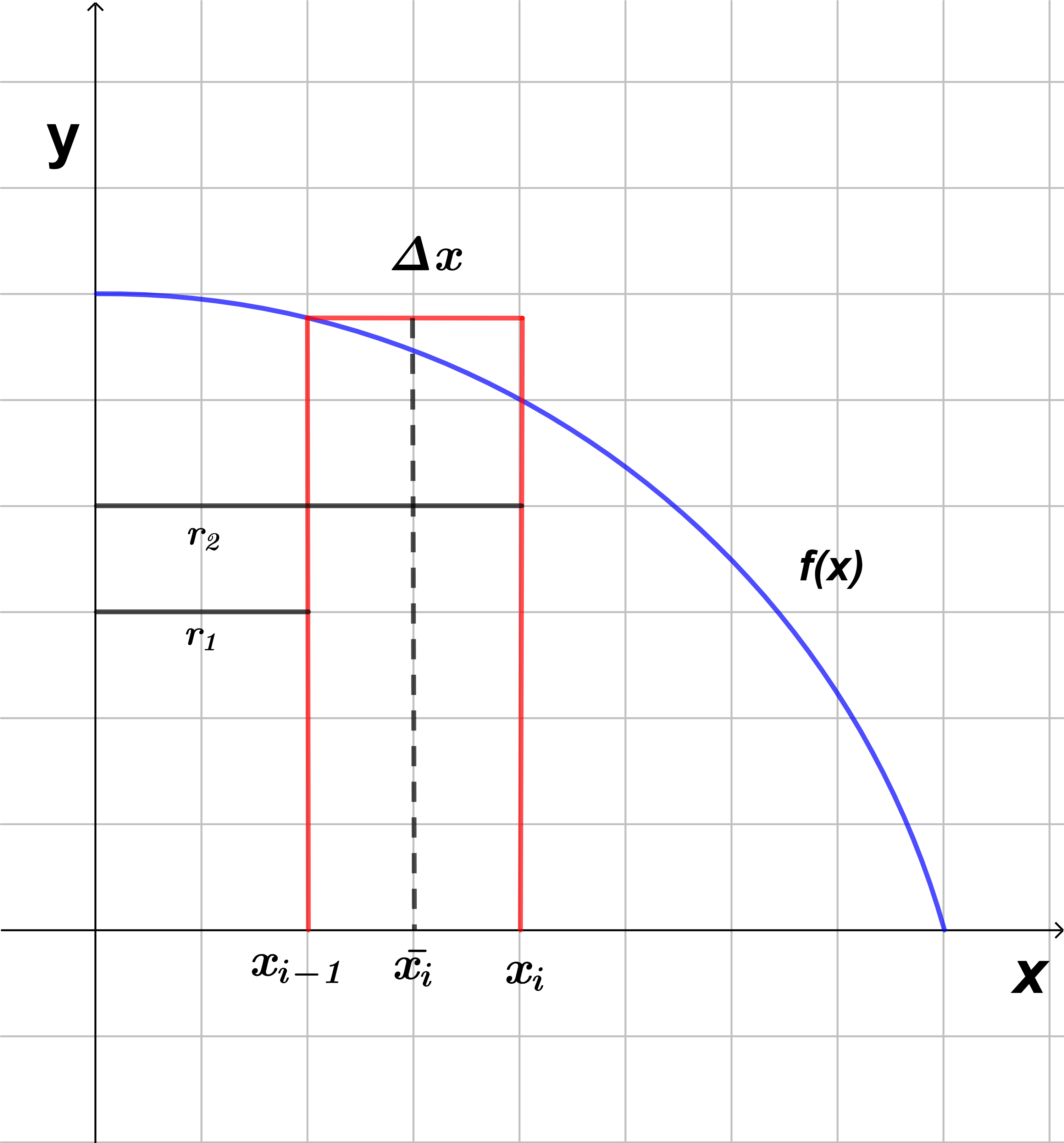
Giramos estas figuras alrededor del eje $y$, la superficie de revolución generado por el polígono es un cascarón cilíndrico de radio exterior $r_{2}$ y radio interior $r_{1}$ como se muestra en la figura $(2)$ (puedes ver mejor la figura haciendo clic sobre la imagen), el volumen $V$ se calcula restando el volumen $V_{2}$ que corresponde al cilindro exterior y $V_{1}$ correspondiente al cilindro interior, por lo que se obtiene que:

$$V=V_{2}-V_{1}=\pi r_{2}^{2}h-\pi r_{1}^{2}h=\pi (r_{2}^{2}-r_{1}^{2})h=\pi (r_{2}+r_{1})(r_{2}-r_{1})h$$

Multiplicamos $\frac{2}{2}$, entonces:

$$V=2\pi \frac{r_{2}+r_{1}}{2}h(r_{2}-r_{1})$$

Sea $r=\frac{r_{2}+r_{1}}{2}$ que es el radio del cascarón cilíndrico y sea $\Delta x=r_{2}-r_{1}$ su grosor, entonces el volumen del cascarón cilíndrico se obtiene como:

$V=2\pi hr \Delta x$

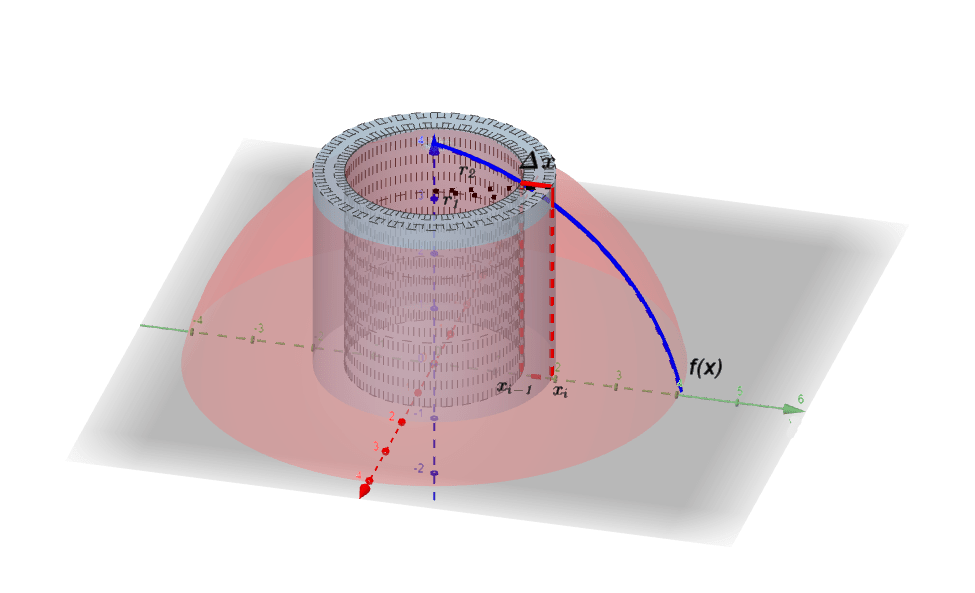
Dividimos el intervalo $[a, b]$ en $n$ subintervalos $[x_{i-1},x_{i}]$ con anchura $\Delta x$ y sea $\bar{x_{i}}$ el punto medio del i-ésimo subintervalo, el sólido generado por el i-ésimo polígono es un cascarón cilíndrico cuyo radio promedio es $\bar{x_{i}}$, altura $f(\bar{x_{i}})$ y espesor $\Delta x$ de modo que el volumen es:

$$V_{i}=2\pi \bar{x_{i}}f(\bar{x_{i}}) \Delta x$$

Un volumen aproximado de $S$ se obtiene al sumar los volúmenes de $n$ cascarones cilíndricos, así:

$$V\approx \sum_{i=1}^{n}V_{i}=\sum_{i=1}^{n}2\pi \bar{x_{i}}f(\bar{x_{i}}) \Delta x$$

Si tenemos que $n \to \infty$ entonces el volumen del sólido que se obtiene al girar alrededor del eje $y$, la región bajo la curva $f(x)$ desde $a$ hasta $b$ está dada como:

$$V=\lim_{n \to \infty}\sum_{i=1}^{n}2\pi \bar{x_{i}}f(\bar{x_{i}}) \Delta x=\int_{a}^{b}2\pi xf(x)dx$$

con $0\leq a\leq b$, a veces, el volumen $V$ se suele escribir como:

$$V=2\pi \int_{a}^{b}R(x)h(x)dx \tag{1}$$

Donde $R(x)$ es la distancia al eje de rotación y $h(x)$ es la altura de corte.

Análogamente, se puede definir el volumen del sólido que se obtiene al girar alrededor del eje $x$, la región bajo la curva $f(y)$ dentro del intervalo $c$ hasta $d$ como:

$$V=2\pi \int_{c}^{d}R(y)h(y)dy \tag{1}$$

Veamos unos ejemplos.

Ejemplos

• Encuentra el volumen del sólido de revolución respecto al eje $y$ de la región acotada debajo de la grafica $f(x)=1-2x+3x^{2}-2x^{3}$ en $[0, 1]$

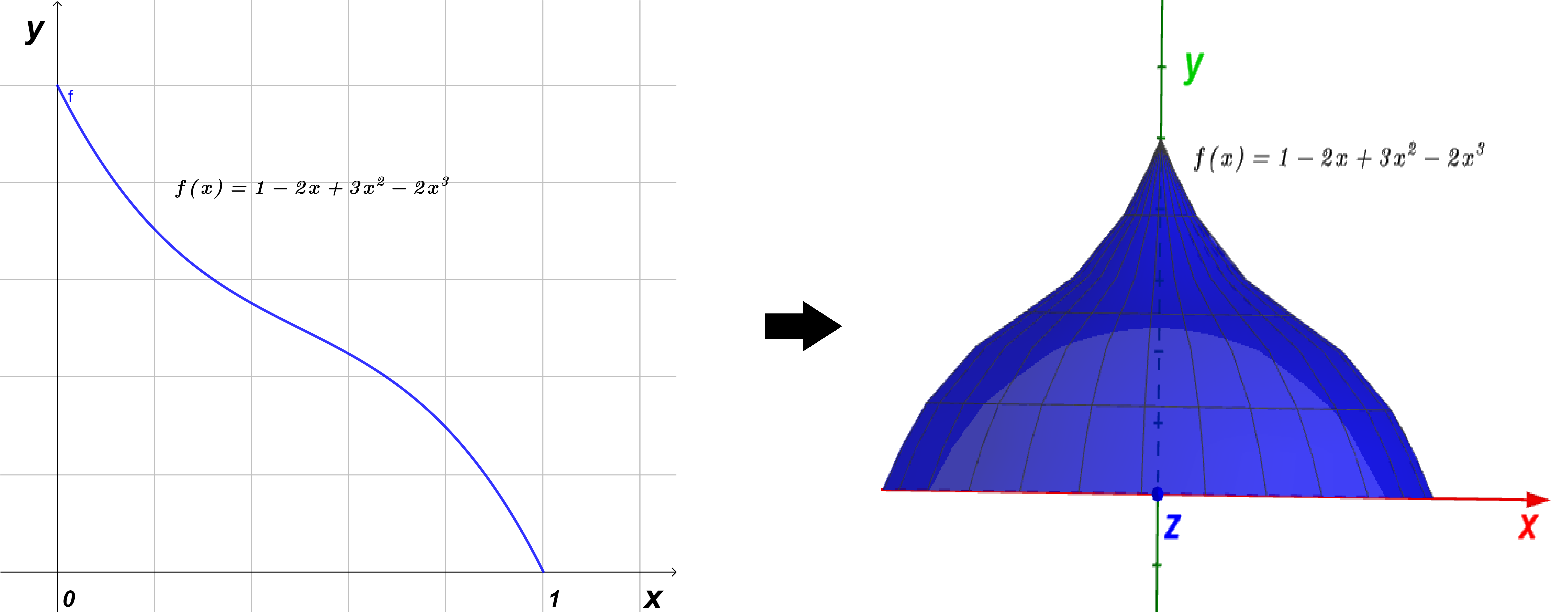
Graficamos la función $f(x)$ en la figura $(3)$ (figura de la izquierda), y la figura de la derecha es el sólido de revolución que es generado por esta función, vemos que la altura está dada por la función $h(x)=f(x)=1-2x+3x^{2}-2x^{3}$ en $[0, 1]$ y el radio $R(x)$ es $x$ por lo que utilizamos la relación $(1)$ para calcular el volumen como:

$$V=2\pi \int_{0}^{1}x(1-2x+3x^{2}-2x^{3})dx=2\pi \int_{0}^{1}(x-2x^{2}+3x^{3}-2x^{4})dx$$

$$=2\pi \left ( \frac{x^{2}}{2}-\frac{2}{3}x^{3}+\frac{3}{4}x^{4}-\frac{2}{5}x^{5} \right )\bigg|_{0}^{1}=2\pi (\frac{1}{2}-\frac{2}{3}+\frac{3}{4}-\frac{2}{5})=\frac{11\pi}{20}$$

• Encuentra el volumen del sólido de revolución respecto al eje $y$ de la región acotada debajo de las graficas $f(x)=x(5-x)$ y $g(x)=8-x(5-x)$

Veamos donde se intersecan estas funciones, para esto igualamos las funciones:

$x(5-x)=8-5x-x^{2} \Rightarrow 2x^{2}-10x+8=0 \Rightarrow x^{2}-5x+4=0 \Rightarrow (x-4)(x-1)=0$

Por lo que vamos a integrar de $x=1$ a $x=4$.

Graficamos las dos gráficas como se ve en la figura $(4)$ (figura de la izquierda), y la figura de la derecha es el sólido generado por estas gráficas, vemos que en el sólido generado se tiene una especie de cono en el centro, el volumen que nos interesa es lo que está afuera de ese cono. La altura de este sólido de revolución es:

$$h(x)=f(x)-g(x)=x(5-x)-8+5x-x^{2}=5x-x^{2}- -8+5x-x^{2}=-8+10x-2x^{2}$$

y

$$R(x)=x$$

Así el volumen la calculamos como:

$$V=2\pi \int_{1}^{4}x(-2x^{2}+10x-8)dx=2\pi \int_{1}^{4}(-2x^{3}+10x^{2}-8x)dx$$

$$=2\pi \left [ -\frac{1}{2}x^{4}+\frac{10}{4}x^{3}-4x^{2} \right ]\bigg|_{1}^{4}=2\pi \left [-128+\frac{640}{3}-64 \right ]-\left [-\frac{1}{2}+\frac{10}{3}-4 \right ]=45\pi$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Encuentra el volumen del solido de revolución respecto al eje $y$ de la región acotada debajo de la grafica $f(x)=2x^{2}-x^{3}$ y $y=0$
2. Encuentre el volumen del solido de revolución respecto al eje $x$ de la región acotada debajo de la grafica $f(x)=9-x^{2}$ en $[0, 3]$
3. Encuentra el volumen del solido de revolución respecto al eje $y$ de la región acotada debajo de la grafica $f(x)=x^{2}+1$ y las rectas $x=0$ y $x=1$
4. Encuentre el volumen del solido de revolución respecto al eje $y$ de la región acotada debajo de las graficas $y=x$ y $y=x^{2}$
5. Encuentra el volumen del solido de revolución que se obtiene al girar alrededor de la recta $x=2$ la región definida por $y=x-x^{2}$ y $y=0$

Más adelante…

En esta entrada aprendimos a calcular el volumen de un sólido de revolución por el método de capas cilíndricas generado alrededor de un eje o una recta específica, en la siguiente sección veremos como calcular el área de una superficie de revolución.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral II.
• Entrada anterior del curso: Cálculo Diferencial e Integral II: Cálculo de volúmenes por secciones transversales y por rotación alrededor de un eje – El blog de Leo (nekomath.com)
• Siguiente entrada del curso: Cálculo Diferencial e Integral: Área de una superficie de revolución – El blog de Leo (nekomath.com)