Introducción
Es de vital importancia conocer el modelo de interés compuesto, así como su fenómeno de acumulación que es el que lo caracteriza, pero también es igual de importante poder conocer la forma en que se puede calcular el valor de hoy, el valor presente de una obligación futura, saber cuánto se deberá pagar en un futuro cierta deuda adquirida el día de hoy, nos permite conocer cuánto se debe de ahorrar el día de hoy para garantizar el pago de dicha obligación. Por ejemplo, si una persona desea adquirir algún bien, una casa, por ejemplo, o una empresa si desea después de cierto tiempo hacer cambio de su mobiliario o de su maquinaria, o de su equipo de cómputo. Todo lo anterior son ejemplo de la utilidad que tiene el saber calcular el valor presente, que como se observa a simple vista, permite encontrar una solución ante todas éstas situaciones.
Valor Presente
Aunque anteriormente ya se había hecho uso, el modelo que describe el fenómeno de valor presente, es el siguiente:
$K=\frac{M}{(1+i)^t}=M(1+i)^{-t}.$
Lo anterior se puede expresar de esa forma porque, recordando una de las leyes de los exponentes $\frac{1}{a^x}=a^{-x}.$
Por lo tanto, el modelo que se va a estudiar es:
$$K=M(1+i)^{-t}.$$
Es una ecuación que ya había sido deducida directamente del modelo de interés compuesto, en el tema anterior, y al ser parte de dicho modelo, las reglas que rigen a la fórmula de interés compuesto, rigen de igual forma a ésta expresión. Es importante señalar que la expresión que se acaba de presentar como Valor Presente, es fundamental en muchos cálculos que se estarán obteniendo, es por ésa razón que a continuación se va a establecer una forma más simplificada de expresarla, la cual es la siguiente:
$$v_1=\frac{1}{1+i}$$
esto es una expresión cuando $t=1.$
Ahora cuando expresamos $t$ de forma general, la expresión queda:
$v_i^t=\frac{1}{(1+i)^t}=(1+i)^{-t}.$
Por último, sustituyendo dicha expresión en el modelo de valor presente:
$$K=Mv_i^{t}.$$
El motivo de usar una $v.$
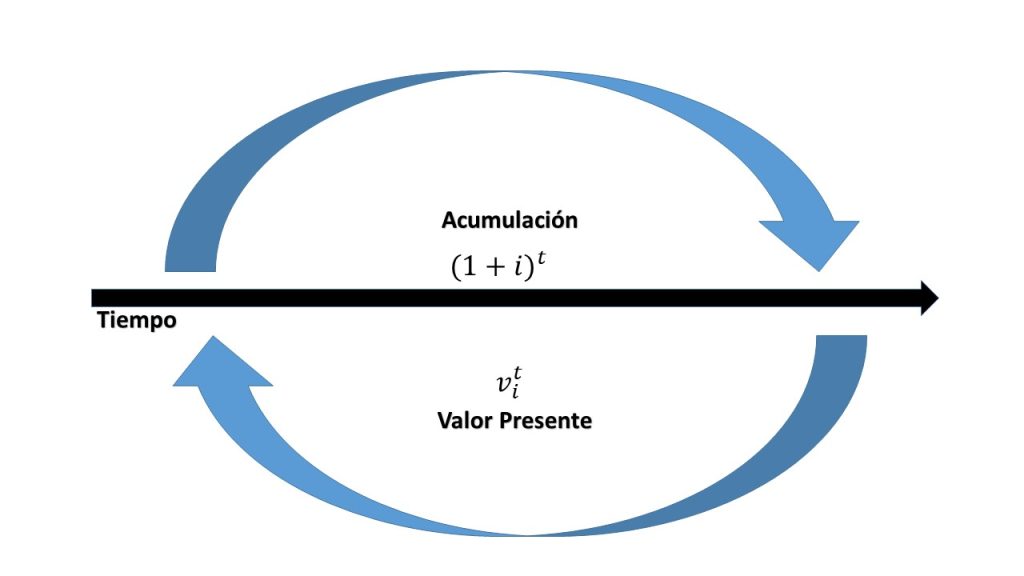
De acuerdo con la imagen, el valor presente es la función inversa del proceso de acumulación de capital, de manera tal que, mantienen una relación que consiste en, que a mayor tasa de interés corresponde una mayor disminución del valor presente del monto. Además, la imagen anterior muestra el proceso de acumulación en comparación al del valor presente, cada una con sus respectivas expresiones algebraicas que los definen.
Tabla de equivalencias entre periodos
A lo largo de estos temas, se puede hacer notar que cada uno de los negocios, convenios, pactos, préstamos, inversiones, etc. tienen en común que tienen una fecha de vencimiento, una fecha de pago, una fecha de cobro, etc. Entre otras cosas, también aparecen las condiciones en las que se realizará sea cual sea la operación, que como ya se ha visto son: tasa de interés, monto inicial, periodo de tiempo, cada cuando se realizaran los pagos. Debido a lo anterior, es necesario establecer ciertos «convenios» en lo que se refiere a la periodicidad de los pagos, con la finalidad de hacer los cálculos de la forma consistente y que sea aplicable a la realidad que describe el fenómeno que se está estudiando.
Con base a lo ya dicho, se presenta a continuación, la siguiente tabla:
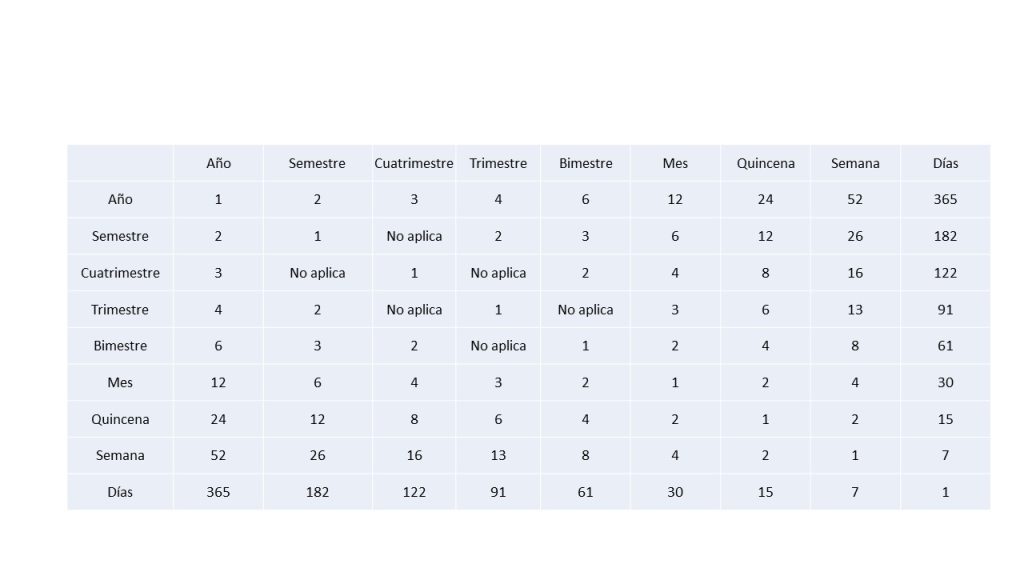
Elaboración propia, basada en Cánovas T. Matemáticas Financieras, Fundamentos y aplicaciones, Ed. Trillas, pag. 38.
En la tabla anterior, se establece de forma general el tiempo, para dar a conocer la forma en que se van a estar usando con fines prácticos, sin embargo; es pertinente señalar que cuando se trate de inversiones, por ejemplo, las que manejan los bancos, es necesario hacer uso del total de días que tiene el mes, esto es, 30 o 31 días en algunos meses, ó 28 o 29 en el caso del mes de febrero, esto debido a que los tipos de inversión consideran el pago de intereses el último día de cada mes.
También, es necesario establecer el número de decimales con el cual se estará realizando los cálculos, estos son al menos 5 decimales, con éste último redondeado. Y el resultado final se deberá ser presentado sólo con dos decimales.
Ejercicios resueltos
Ejercicio. Calcular el valor presente o traer a valor presente, a la fecha de hoy, la cantidad de \$2000 que deberán pagarse dentro de un año a una tasa de interés efectiva semestral del 7%.
Solución
Haciendo uso del modelo de valor presente: $v_i^{t}$,
Sustituyendo los datos, se tiene:
$X=(2000)\frac{1}{(1+.07)^2}$
lo que también es equivalente a escribir:
$X=2000(1+0.07)^{-2}$
Lo que resulta \$1746.8774, una cantidad que es menor a \$2000, esto se debe a que está representando su valor presente, pero de igual forma, si invertimos la cantidad de \$1746.8774 durante un año, justamente se obtendrá el valor de \$2000.
Es pertinente hacer mención que no necesariamente el valor presente se debe calcular a la fecha del día de hoy, éste puede ser calculado en cualquier fecha siempre y cuando sea antes de la fecha de vencimiento o del pago de la obligación.
Ejercicio. Para este ejemplo, se va a suponer que el día de hoy es 2 de octubre, y una empresa de ropa tiene contemplado saldar la deuda de un pagaré con un valor de \$85000, con fecha de vencimiento 30 de mayo, del siguiente año. En dicha deuda se acordó una tasa efectiva del 10% anual. Dicha empresa se propone saldar su deuda, aprovechando la temporada decembrina que tiene ventas e ingresos extras, para el día 30 de diciembre.
Solución
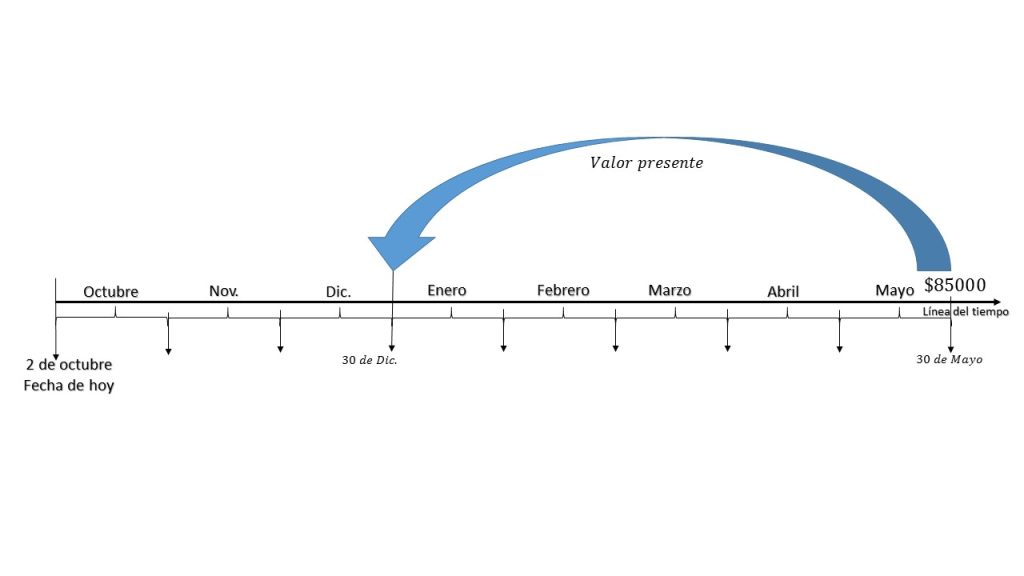
Suponemos también que no existe ningún tipo de penalización por liquidar la deuda de forma anticipada, en tal caso la ecuación queda:
\begin{align*}
X&=85000(v_{0.10}^{\frac{5}{12}})\\
X&=85000(1+0.10)^{-\frac{5}{12}}\\
X&=81690.5788\\
\end{align*}
Por lo tanto, para liquidar la deuda, se tiene que hacer un pago de \$81690.5788 el 30 de diciembre.
Es importante hacer mención que si no ha transcurrido tiempo en alguna operación, el monto y el valor presente del dinero no sufre cambios, cuando se quiere a traer a valor presente en la misma fecha que debe ser pagado, es decir; Si el día de hoy 26 de septiembre de 2005 (por ejemplo), nos prestan \$10 pesos, y calculamos el valor presente en ésa misma fecha, el resultado será igual \$10.
Ejercicio. Se quiere calcular el monto de una cantidad $X$ durante un tiempo cero, $t=0$ con una tasa de interés $i.$
Solución
Aplicando el modelo de interés compuesto se tiene:
$M=X(1+i)^0.$
Recordamos que cualquier potencia elevada a cero nos da un resultado igual a 1, esto es: $a^0=1$, o lo que aplica a nuestro modelo: $(1+i)^0$
Lo cual implica que: $M=X(1+i)^0=X(1)$
$$M=X.$$
Lo anterior, se sigue cumpliendo si ahora queremos calcular el valor presente con los mismos supuestos de un tiempo cero. Esto es:
$Xv_i^{t=0}=X(1+i)^0=X(1)=X.$
Más adelante…
A lo largo de estos temas se ha estudiado cómo el dinero modifica su valor con el paso del tiempo, en particular los dos casos que acaban se ser abordados, proceso de acumulación y valor presente. Se ha visto el comportamiento de las tasas efectivas de interés, dentro del modelo de interés simple como de interés compuesto. Un aspecto importante que no se debe de restar importancia, es al fenómeno en el que queremos calcular el valor presente en un tiempo cero, esto es, el mismo día que se emite el préstamo, fecha en la que cual el monto y el valor presente son el mismo. Lo anterior adquiere mucha importancia sobre todo, cuando se construya una ecuación de valor, tema que pronto será abordado.
Entradas relacionadas
- Ir a Matemáticas Financieras
- Entrada anterior
- Entrada siguiente
