Introducción
Este tema será abordado, haciendo uso de los conocimientos adquiridos en el tema de anualidades crecientes, tomando en cuenta sus reglas del modelo de interés compuesto, así como la equivalencia entre las tasas de interés.
Concepto y descripción
El proceso de construcción de la tabla de amortización para créditos con pagos crecientes, es análogo a como se han venido construyendo en los temas anteriores, con la única diferencia que ahora se estarán aplicando el concepto de anualidades crecientes.
Para dejarlo más en claro se procederá a realizar el siguiente ejemplo:
La señora Juanita quiere irse de vacaciones, y ha estado haciendo cuentas para saber a cuánto ascienden sus ingresos, los resultados que obtuvo son que puede disponer de una cantidad de \$5000 de forma mensual, y pretende tener un incremento a ésa cantidad de \$500 pesos cada mes. Desea saber ¿cuánto le podrían prestar si pide un crédito a una caja de ahorro popular, bajo ésta situación. si su deseo es pagar dicho crédito en año y medio, con una tasa de interés del 3% efectivo mensual.
Para poder encontrar la respuesta a éste problema se realizará primeramente el cálculo de la cantidad que se le puede otorgar por parte de la institución financiera.
Para ello se aplicará la siguiente ecuación de valor:
$$M=5000\prescript{}{18}{\mathbf{A}}_{.03}+500\left(\frac{\prescript{}{18}{\mathbf{A}}_{.03}-18v_{0.03}^{18}}{0.03}\right)$$
$$\prescript{}{18}{\mathbf{A}}_{.03}=\left(\frac{1-v_{0.03}^{18}}{0.03}\right)=\left(\frac{1-\left(\frac{1}{1+0.03}\right)^{18}}{0.03}\right)=13.7535131.$$
Sustituyendo el valor que se acaba de obtener:
$$M=5,000(13.7535131)+500\left(\frac{13.7535131-10.5731029}{0.03}\right)$$
$$M=68,767.56550+500\left(\frac{3.1804102}{0.03}\right)$$
$$M=68,767.56550+53,006.83632=121,774.4018.$$
La cantidad que se le puede otorgar a la señora Juanita es de \$121,774.40
y la tabla de amortización queda como sigue:
Ejercicios resueltos
Ejercicio. Una empresa desea constituir una reserva para hacer frente a contingencias que pudiera tener, con la finalidad de no verse afectada por gastos inesperados. Por este motivo se propone ahorrar durante un año, para ver cuánto puede generar, ya que las aportaciones las hace de forma mensual y en base a sus ingresos, los cuales ascienden a \$2 mil pesos mensuales y planea incrementar en \$300 pesos cada mes, con una tasa de interés del 4% mensual.
Se necesita calcular el monto que se va a obtener durante la vigencia del tiempo que va a ahorrar, y elaborar la tabla de amortización, de éste problema.
Solución
La ecuación de valor es la que se trabajo en ésta sección, la cual es:
$$M=2000\prescript{}{12}{\mathbf{A}}_{.04}+300\left(\frac{\prescript{}{12}{\mathbf{A}}_{.04}-18v_{0.03}^{12}}{0.04}\right)$$
$$M=2,000(9.3850738)+300\left(\frac{9.3850738-7.4951640}{0.04}\right)$$
$$M=28155.22128+300\left(\frac{1.8899098}{0.04}\right)$$
$$M=28155.22128+300(47.2477450)$$
$$M=28155.22128+14174.32350=42329.54478$$
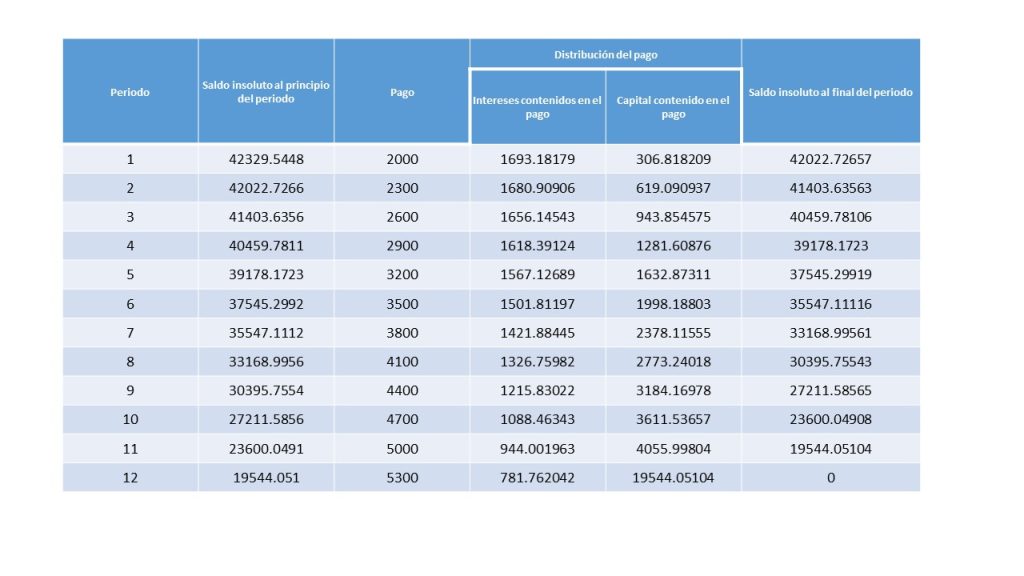
Y la tabla de amortización queda:
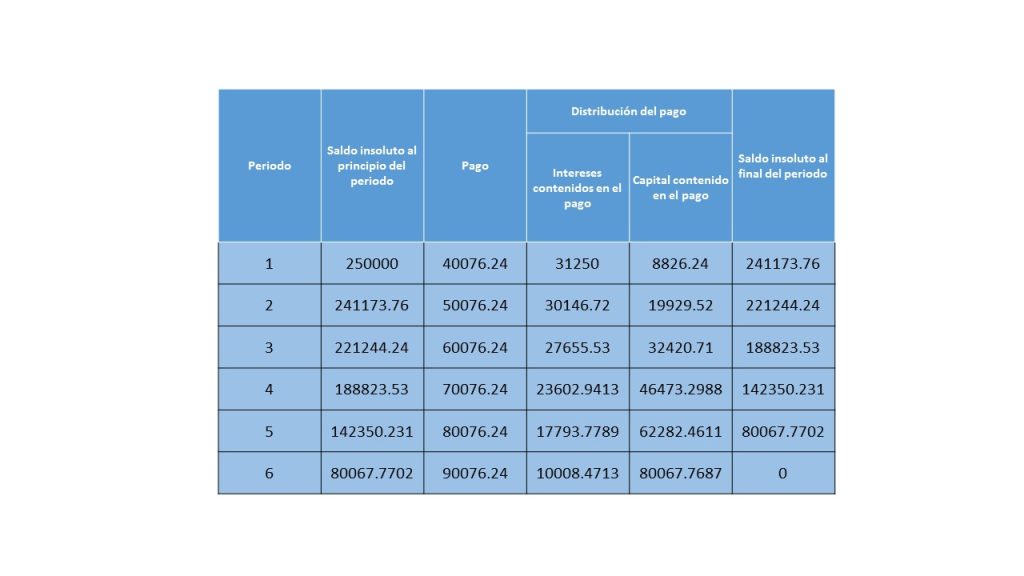
El señor Ramón, desea conocer la forma en que va a pagar el crédito que le otorgo el banco a su empresa textil, para ampliación de sus instalaciones. La cantidad que le otorgó fue de \$250 mil pesos, con una tasa de interés del 25% semestral, si cada pago será realizado de forma semestral, por la cantidad de \$40,076.24 el cual irá incrementándose en \$10 mil pesos, durante 3 años.
Solución
Lo único que hay que realizar es, poner en práctica la forma en que se construye la tabla de amortización, la cual, siguiendo los pasos de forma análoga a como se ha venido haciendo, queda de la siguiente forma:
Más adelante…
Se abordaran la construcción de tablas de amortización que combinan su construcción con otros tipos de anualidades, y que van a estar presentes en una misma tabla.
- Ir a Matemáticas Financieras
- Ir a Entrada Anterior
- Ir a Entrada Siguiente