Introducción
Éste tipo de anualidades, se presentan cuando las personas hacen la solicitud de un crédito, y éste considera un periodo de «gracia», el cual es un tiempo considerable que les otorgan por ejemplo mientras se hacen de una buena cartera de clientes, considerando el hecho de que, al ser una nueva empresa, no va a ser posible generar ingresos desde el día uno. Sin embargo, dicho periodo, sí está generando intereses, pero aun con eso, le permite a la persona que adquirió el crédito el no tener que estar pagando de forma inmediata dicha deuda.
Descripción y valor presente
Las anualidades diferidas, son el tipo de anualidades en las que no se realizan los pagos desde el primer periodo, sino después de haber transcurrido el periodo de gracia que se haya pactado, el cual puede ser un período o más. Un ejemplo de éste tipo de créditos, son las promociones que sacan en el buen fin, «disfrute hoy de su pantalla, coche, o lo que sea que estén vendiendo y pague hasta enero del siguiente año».
De acuerdo a lo anterior, una anualidad diferida, es la que establece un plazo en el que no se va a realizar ningún pago, a dicho periodo se le conoce como diferimiento, y una vez transcurrido éste, se da inicio a la realización de los pagos de la forma conocida como una anualidad.
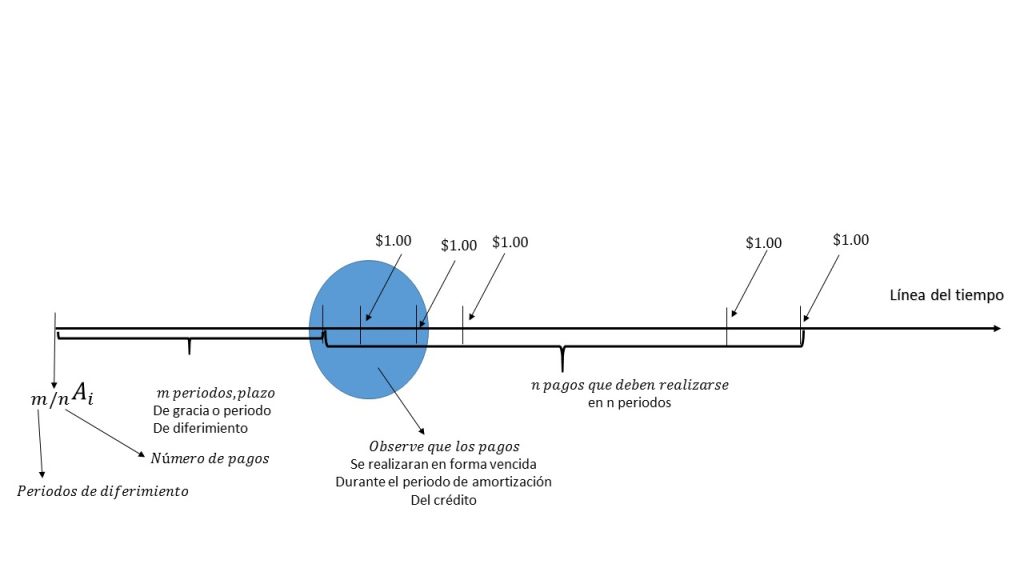
Una anualidad diferida es denotada por:
$$\prescript{}{m/n}{\mathbf{A}}_i=v_i^{m+1}+v_i^{m+2}+…+v_i^{m+n-2}+v_i^{m+n-1}+v_i^{m+n}$$
$$\prescript{}{m/n}{\mathbf{A}}_i=v_i^m(v_i^1+v_i^2+…+v_i^{n-2}+v_i^{n-1}+v_i^n)$$
$$\prescript{}{m/n}{\mathbf{A}}_i=v_i^m\prescript{}{n}{\mathbf{A}}_i$$
$$V=X\prescript{}{m/n}{\mathbf{A}}_i$$
$$V=X\prescript{}{m/n}{\mathbf{A}}_i=Xv_i^m\prescript{}{n}{\mathbf{A}}_i.$$
Reglas para su uso
- $m$ y $n$ son número enteros y se miden en la misma temporalidad, esto es, si n son semanas, m serán también semanas
- Los pagos se realizan de forma vencida, esto quiere decir que el primer pago se realizará al final del primer periodo que aparezca, una vez que haya concluido el periodo de gracia o periodo de diferimiento.
- La tasa de interés deberá ser efectiva por periodo, para los $n$ pagos, así como los $m$ periodos que conformen el periodo de diferimiento.
Monto
Para obtener el monto de una anualidad diferida, de forma semejante a las dos anualidades vistas anteriormente (anticipadas y vencidas), se continua tomando como referencia para su valuación, la fecha en la que realizo el último pago.
En la siguiente imagen, se muestra lo que se acaba de mencionar:
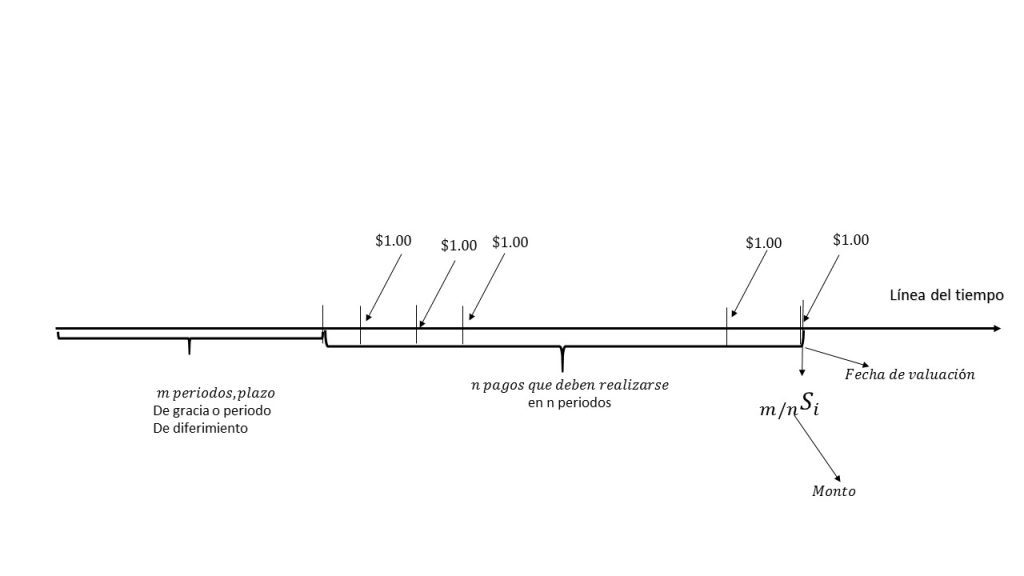
La expresión con la que se va a denotar una anualidad diferida es:
$$\prescript{}{n}{\mathbf{S}}_i=(1+i)^{n-1}+(1+i)^{n-2}+…+1$$
de donde se obtiene:
$$\prescript{}{n}{\mathbf{S}}_i=\frac{(1+i)^n-1}{i}.$$
De forma análoga a las anteriores anualidades, ésta expresión denota los pagos con valor de \$1.00, para hacerlo de forma más general se considera pagos de cantidad $X, y la expresión queda:
$$M=X\prescript{}{n}{\mathbf{S}}_i=X\frac{(1+i)^n-1}{i}.$$
En este momento, ya se tienen 3 tipos de anualidades, por lo que ya se cuenta con el material necesario para resolver problemas que involucran combinaciones entre ellas.
Ejercicios resueltos
Ejercicio. Una persona necesita un crédito por \$80,000 para reparar su vehículo, ya que es modelo antiguo y lo quiere volver un coche clásico. El banco decide otorgarle el crédito, y además le otorga un periodo de gracia por 4 meses, comenzando a pagar a partir del final del quinto mes. La deuda debe ser pagada en 24 mensualidades. Se desea saber la cantidad que tendrán dichas mensualidades, con una tasa del 1.5% efectivo mensual.
Solución
Aplicando el modelo de la ecuación de valor se tiene:
$$80,000=X\prescript{}{4/24}{\mathbf{A}}_{0.015}$$
$$X=\frac{80,000}{\prescript{}{4/24}{\mathbf{A}}_{0.015}}$$
$$X=\frac{80,000}{v_{0.015}^{4}}\prescript{}{4/24}{\mathbf{A}}_{0.015}$$
$$X=\frac{80,000}{(0.9421847)(20.03038)}=4239.01.$$
La cantidad que deben de pagar cada mes es de \$4239.
Ejercicio. Supongamos que una persona contrata un crédito por \$100,000 y lo quiere liquidar en 10 mensualidades vencidas con pagos de \$4000, posteriormente realizará pagos durante 8 mensualidades iguales, que serán pagadas luego de un periodo de gracia de 6 meses. Se necesita saber ¿Cuánto es el monto de las 8 mensualidades, a una tasa de interés del 1.3% mensual?
Solución
Éste es un claro ejemplo que combina 2 anualidades, una vencida y la otra diferida. En la siguiente imagen se ilustra el modelo que se va a tomar para su respectiva solución.
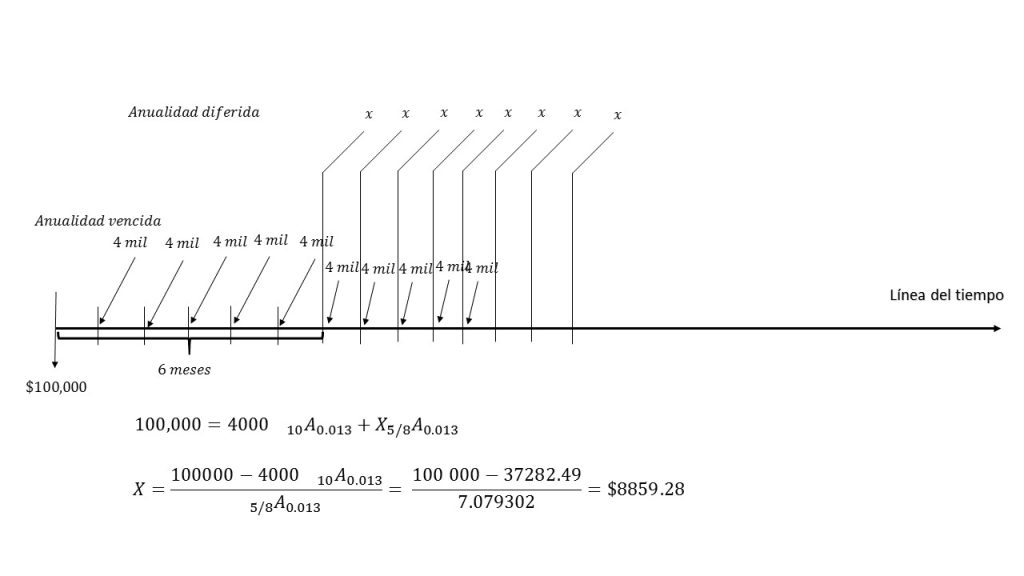
El monto que se obtendrá es de \$8859.28.
Más adelante…
En las siguientes secciones se continuará otros tipos de anualidades, su combinación entre ellas, la forma en que se aplican para la resolución de problemas.
Entradas relacionadas
- Ir a Matemáticas Financieras
- Entrada anterior
- Entrada siguiente
