Introducción
En éste apartado, se abordarán las anualidades opuestas a las que acabamos de revisar, las anualidades decrecientes, las cuales como su nombre lo indica su principal característica, es que conforme avanza el tiempo van disminuyendo. Su uso se presenta en los casos en los que se otorga un préstamo, un crédito, en el que el bien adquirido con el paso del tiempo se va deteriorando, es decir; cuando están nuevos y recién adquiridos requieren un mantenimiento mínimo, sin embargo; con el paso del tiempo y el uso, van necesitando cada vez mantenimientos más costosos, y si a ello se le agrega que aún no se terminan de pagar, pues este tipo de anualidad se amolda muy bien a ésta situación, en la que al deudor le conviene bastante que en el momento en el que se requieran servicios más costosos, se pague cada vez menos a la deuda adquirida, sin que por ello se omita o incumpla alguna obligación. Todo este acuerdo, se pacta desde un inicio entre las partes involucradas.
Descripción y valor presente
Una anualidad decreciente, es aquella que conforme avanza el tiempo, los pagos que se van realizando cada vez son menores, el objetivo de este tipo de anualidad es que la persona deudora este en las condiciones de poder cumplir cómodamente con sus obligaciones, al mismo tiempo que la institución que otorga el crédito o préstamo no vea afectado la recuperación de sus recursos ni asuma un riesgo mayor.
Éste tipo de anualidad, tiene como característica principal que cada pago realizado es igual al anterior menos una cierta cantidad. Otra característica importante es que comienza con un pago de cierto valor, llamémoslo $n$ y los pagos siguientes van a ir disminuyendo una cierta cantidad, hasta llegar al último pago con valor igual a un peso.
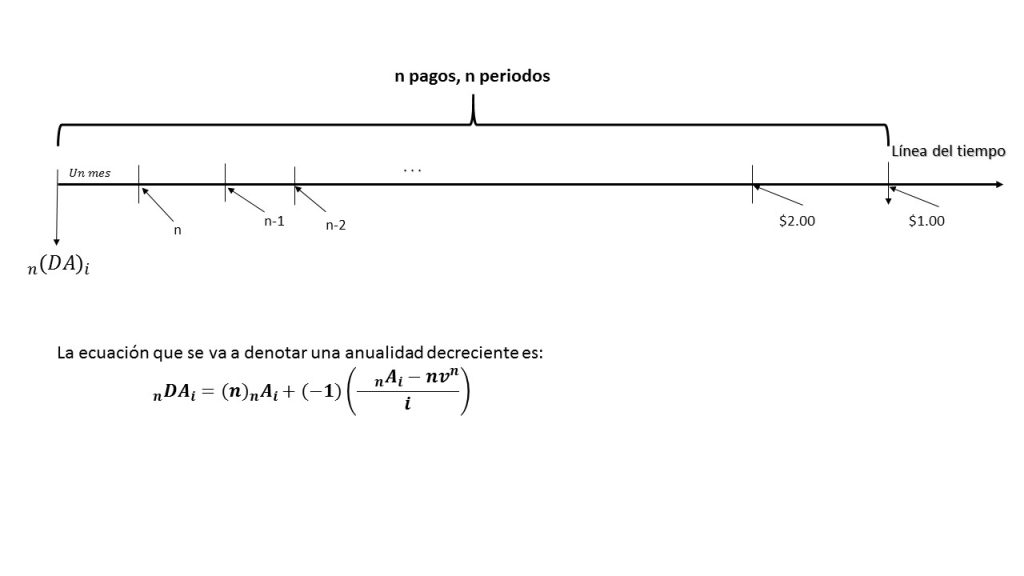
El valor presente de esta anualidad se denota por:
$$\prescript{}{n}{\mathbf{(DA)}}_i$$
donde:
- $D$ hace referencia a la palabra decreasing (decreciente).
- $n$ es el número de pagos que se van a realizar.
- $i$ continúa representando la tasa de interés efectiva por periodo.
Para obtener el valor presente de dicha anualidad, se partirá de la siguiente expresión:
$$\prescript{}{n}{\mathbf{(DA)}}_i=(n)\prescript{}{n}{\mathbf{A}}_i+(-1)\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$
Luego:
$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{in\prescript{}{n}{\mathbf{A}}_i-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}.$$
Recordando, que $\prescript{}{n}{\mathbf{A}}_i=\frac{1-v^n}{i}$, la expresión anterior se convierte en:
$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{in\left(\frac{1-v^n}{i}\right)-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}.$$
Luego, cancelando las $i$ del numerador y multiplicando por $n$ la expresión que está entre paréntesis, se obtiene:
$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{n(1-v^n)-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}=\frac{n-nv^n-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}.$$
Por último, reducimos términos:
$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{n-\prescript{}{n}{\mathbf{A}}_i}{i}.$$
Para generalizar la expresión, se toma como primer pago a $P$ y los pagos siguientes disminuyen una cantidad $Q$, pero se debe de tener cuidado con el último pago, $P-(n-1)Q$, sea positivo; esto es que $P$ debe ser mayor a $(n-1)Q.$
Entonces, la ecuación para calcular el valor presente seria:
$$V=P\prescript{}{n}{\mathbf{A}}_i-Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$
Monto
El monto de una anualidad decreciente, con $n$ pagos que se aportarán durante $n$ periodos, fijando el primer pago $n$ y los pagos siguientes irán disminuyendo en una unidad, se calcula de forma similar a los crecientes, y es denotada por:
$$\prescript{}{n}{\mathbf{SD}}_i=\frac{n-\prescript{}{n}{\mathbf{A}}_i}{i}(1+i)^n.$$
En este tipo de anualidad decreciente, el primer pago será $P$ mientras que los pagos siguientes serán disminuidos por una cantidad $-Q$, la expresión queda denotada por:
$$V=P\prescript{}{n}{\mathbf{A}}_i(1+i)^n-Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right)(1+i)^n.$$
Por último, el monto de una anualidad geométrica decreciente con razón $(1-K)$ es:
$$V=X\left(1-\frac{(1-k)^n}{(1+i)^n}\right)\left(\frac{(1+i)^n}{1+k}\right).$$
Ejercicios resueltos
Ejercicio. Una empresa de aeronaves, necesitan refacciones para sus aviones, sus socios desean adquirir un crédito para ello, y planean pagarlo con aportaciones decrecientes, las cuales están basadas en su experiencia de ingresos. Al hacer sus cálculos, llegan a la conclusión de que cada uno de sus socios pueden realizar aportaciones mensuales de forma vencida, comenzando con un adelanto de \$6 mil pesos, disminuyendo los siguientes pagos en \$250, hasta llegar a mensualidades de \$2 mil. Pretenden, además, negociar, para que el banco les otorgue un plazo para pagar su crédito de 2 años, a una tasa de interés del 10.5% pagadero mensual el banco les otorga una plazo de año y medio. ¿Se necesita saber qué cantidad es la que el banco puede prestar a cada uno de sus socios?
Solución
Para resolver éste problema, lo que se necesita es hacer uso del concepto de valor presente de una anualidad decreciente, el cual, va a ser más el valor presente de una anualidad vencida de pagos iguales por la cantidad de \$2,000.
La anualidad decreciente consistirá en:
$$\frac{6,000-2,000}{250}+1=16$$
de esta forma se obtiene el número de pagos por el que se encuentra formada nuestra anualidad decreciente, siendo el primer pago de \$6,000 y el último de \$2,000.
Tomando en cuenta, que el plazo total que se les ha otorgado es de año y medio, eso implica que habrá 2 mensualidades adicionales de \$2,000 cada una. De esta forma, la ecuación que se va a utilizar para resolver éste problema es:
$$V=6,000\prescript{}{16}{\mathbf{A}}_{0.0125}-250\left(\frac{\prescript{}{16}{\mathbf{A}}_{0.0125}-16v_{0.0125}^{16}}{0.0125}\right)+250\prescript{}{2}{\mathbf{A}}_{0.0125}v_{0.0125}^{16}$$
$$=6,000(14.4202)-250\left(\frac{(14.4202)-16(0.8197463)}{0.0125}\right)+250(1.9631)(0.9754611)$$
$$=86,521.2-250(104.3407360)+478.731921$$
$$=86,521.2-26085.184+478.731921=60914.74792$$
La cantidad que se les podría otorgar a los socios es: \$60,914.74792
Ejercicio. Una empresa de restaurantes, desea abrir una sucursal en el pueblito abc, para llevarlo a cabo ha considerado una inversión de \$250 mil pesos. El dueño en base a su experiencia, aspira a tener ingresos de la siguiente forma:
- Considera poder hacerse de clientes durante los primeros 2 años, por lo que calcula tener ingresos en el primer mes de cada periodo de \$3000 pesos, los cuales irán incrementando \$800 pesos cada periodo durante los meses restantes (23 meses).
- Espera que las ventas se mantengan estables en los 2 años que siguen, ingresos de \$6 mil
- En el último año considera tener ingresos de \$7 mil pesos, con una posible caída de ventas de \$200 pesos mensuales hasta el término de dicho año.
Si el dueño de ése restaurante, espera recuperar su inversión de \$250 mil pesos valuados a la fecha de apertura, así como tener una ganancia de 25% anual. ¿Se necesita saber si con los datos que él dueño planeó, es suficiente para alcanzar sus metas, sobre todo si se propone tener ganancias netas del 35%.
Solución
Para poder resolver éste ejercicio, hay que hacer lo siguiente:
- Traer a valor presente la cantidad de ingresos que planea obtener, durante los 5 años, a la tasa de rendimiento que el dueño pronostica.
- Restar la cantidad que se obtenga en el primer paso, a los costos que consumió el restaurante para poder abrir, esto es el 70%, con esto se obtiene el valor actual de las utilidades esperadas
- Por último, se necesita comparar la inversión realizada. Si el valor presente de las utilidades netas es igual a la inversión realizada, entonces significa que el dueño si pudo recuperar su inversión y que además su restaurante habrá tenido el rendimiento que él consideró tener el cual era de 25% anual.

La tasa de rendimiento esperada es del 25% anual, la cual tiene una tasa equivalente mensual del 0.0187693. Este dato se obtiene de la triple igualdad
$$(1+i)=(1.025)^{\frac{1}{12}}$$
de donde se obtiene $i=0.0187693.$
Ahora, la ecuación de valor que se necesita para resolver este problema es:
$$V=3,000\prescript{}{24}{\mathbf{A}}_{0.0187693}+800\left(\frac{\prescript{}{24}{\mathbf{A}}_{0.0187693}-24v_{0.0187693}^{24}}{0.0187693}\right)$$
$$+6,000\prescript{}{24}{\mathbf{A}}_{0.0187693}
v_{0.0187693}^{24}$$
$$+\left(7,000\prescript{}{12}{\mathbf{A}}_{0.0187693}-200\left(\frac{\prescript{}{12}{\mathbf{A}}_{0.0187693}-12v_{0.0187693^{12}}}{0.0187693}\right)\right)v_{0.0187693}^{48}.$$
Esta ecuación tiene 3 secciones:
La primera, representa el valor presente de la anualidad creciente de los 2 primero años, mientras que la segunda, representa el presupuesto de ventas (\$7000 mensuales) para el tercer y cuarto año.
La última sección pertenece a la anualidad decreciente que conforma el presupuesto de ventas para el quinto año y que se lleva, también, hasta la fecha de valuación multiplicándolo por $v_0.01715^{48}$.
$$v=300,000(19.539037)+80,000(208.82239)+1,400 000(19.539037)(0.6649055)$$
$$+[1,200,000(10.762845)-50,000(57.016793)(0.4420993)$$
$$v=5,861,711.10+16,705,791+27,354,651+4,449,541.50$$
$$v=\$54,371,694.60.$$
Del valor obtenido, aún falta por restarle el \$70% por concepto de costo de ventas, lo que equivale a \38,060,185.40, para obtener el valor presente de los flujos de utilidades netas que brinda el proyecto. De esta forma tenemos la siguiente ecuación:
$$U=54,371,694.6-38,060,185.4=\$16,311,509.2.$$
El resultado obtenido, significa que la inversión si podrá ser recuperada, y que además tendrá un rendimiento mayor al esperado de 23.144% toda vez que el valor presente de las utilidades netas futuras es mayor a la inversión original.
*Éste ejercicio fue basado del libro Matemáticas Financieras, fundamentos y aplicaciones, Cánovas T. Ed. Trillas, pag. 168.
Más adelante…
Se abordarán las anualidades pagaderas p veces al año, las cuales son de gran utilidad cuando se tiene casos en los que lo que se pretende es dar una expresión clara de cómo se puede ir pagando un crédito, conociendo la cantidad que se debe de pagar en cada periodo. Con este tema terminamos de adquirir las herramientas necesarias para poder evaluar proyectos de inversión.
Entradas relacionadas
- Ir a Matemáticas Financieras
- Entrada anterior
- Entrada siguiente
