Introducción
Este tipo de anualidades, se utiliza en los casos en lo que alguien solicita un crédito, y de alguna forma sabe que en el futuro sus ingresos mejorarán, condición que les permitirá poder cada vez dar mayores cantidades, para pagar dicho crédito. Un ejemplo de lo anterior, es cuando una empresa moderniza su maquinaria, y al hacerlo esto le da la condición de poder tener una mayor producción, lo cual genera mayores ingresos, mayor venta y por consecuencia mayores utilidades, las cuales pueden irse incrementando y a través de ellas, logrando con esto, aportar una mayor cantidad para liquidar su deuda.
Descripción y valor presente
Se define como anualidad creciente, al tipo de anualidad que se caracteriza por ir incrementando los pagos en cada periodo, es decir; cada pago se realiza con una cantidad mayor, de manera que los pagos crecerán de forma aritmética. Dichos incrementos son acordados entre las partes involucradas, de acuerdo con la capacidad de pago que tenga el deudor, los cuales estarán basados a partir de los cálculos de sus ingresos futuros.
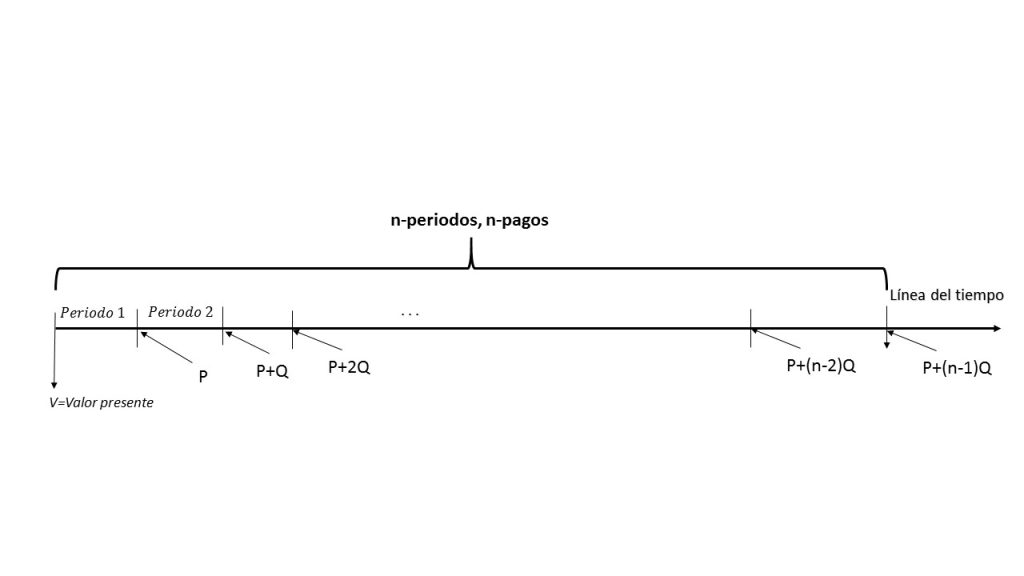
La imagen anterior, muestra gráficamente el comportamiento de una anualidad creciente, así como la forma, en que se convierte en una progresión aritmética.
Si se quiere calcular el valor presente, $V$, en una anualidad creciente, es necesario traer a valor presente cada uno de los pagos, considerando una tasa de interés efectiva por periodo. Esto se puede observar en la siguiente expresión:
$$V=Pv+(P+Q)v^2+(P+2Q)v^3+(P+3Q)v^4+…+[P+(n-2)Q]^{n-1}+[P+(n-1)Q]v^n.$$
Para obtener una expresión más sencilla, se resolverán los productos indicados, es decir:
$$V=Pv+Pv^2+Qv^2+Pv^3+2Qv^3+..+Pv^{n-1}+(n-2)Qv^{n-1}+Pv^n+(n-1)Q^{n}.$$
Ahora, se multiplicará la ecuación, por un uno, de la siguiente forma:
$$1=\left(\frac{1+i}{1+i}\right)$$
aplicándolo a la expresión que teníamos, da como resultado:
$$\left(\frac{v^1}{v^1}\right)V=Pv+Pv^2+Qv^2+Pv^3+2Qv^3+..+Pv^{n-1}+(n-2)Qv^{n-1}+Pv^n+(n-1)Q^{n}$$
$$\left(\frac{(1+i)^1}{(1+i)^1}\right)V=Pv+Pv^2+Qv^2+Pv^3+2Qv^3+..+Pv^{n-1}+(n-2)Qv^{n-1}+Pv^n+(n-1)Q^{n}$$
$$(1+i)V=[Pv+Pv^2+Qv^2+Pv^3+2Qv^3+..+Pv^{n-1}+(n-2)Qv^{n-1}+Pv^n+(n-1)Q^{n}](1+i)^{-1}$$
$$V+iV=Pvv^{-1}+(P+Q)v^2v^{-1}+(P+2Q)v^3v^{-1}+…+[P+(n-2)Q]v^{n-1}v^{-1}+[P+(n-1)Q]v^nv^{-1}$$
$$V+iV=P+(P+Q)v^1+(P+2Q)v^2+…+[P+(n-2)Q]v^{n-2}+[P+(n-1)Q]v^{n-1}$$
$$V+iV=P+Pv+Qv+P^2+2Qv^2+…+Pv^{n-2}+(n-2)Qv^{n-2}+Pn^{n-1}+(n-1)Qv^{n-1}.$$
Restando ésta última expresión, con la segunda que obtuvimos se tiene:
$$V+iV=P+Pv+Qv+P^2+2Qv^2+…+Pv^{n-2}+(n-2)Qv^{n-2}+Pn^{n-1}+(n-1)Qv^{n-1}$$
$$-V=-Pv-Pv^2-Qv^2-Pv^3-2Qv^3-…-Pv^{n-1}-(n-2)Qv^{n-1}-Pv^n-(n-1)Q^{n}.$$
Nos da como resultado:
$$iV=P+Qv+Qv^2+Qv^3+…+Qv^{n-1}-Pv^n-(n-1)Qv^n.$$
Haciendo las multiplicaciones indicadas, se obtiene:
$$iV=P+Qv+Qv^2+Qv^3+…+Qv^{n-1}+Qv^n+Pv^n-nQv^n.$$
Factorizando $Q$ se tiene:
$$iV=P+Q(v+v^2+v^3+…+v^{n-1}+v^{n})-Pv^n-nQv^n.$$
Factorizando ahora a $P$:
$$iV=P(1-v^n)+Q\prescript{}{n}{\mathbf{A}}_i-nQv^n$$
lo anterior, ocurre porque $\prescript{}{n}{\mathbf{A}}_i= v+v^2+v^3+…+v^{n-1}+v^{n}$
de donde, se despeja a $V$ para obtener:
$$V=P\left(\frac{1-v^n}{i}\right)+Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$
Tomando en cuenta que $\prescript{}{n}{\mathbf{A}}_i=\frac{(1-v^n)}{i}$, y sustituyendo dicho valor en la ecuación anterior, se tiene por fin la expresión más sencilla para el cálculo del valor presente de una anualidad creciente con $n$ pagos:
$$V=P\prescript{}{n}{\mathbf{A}}_i+Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$
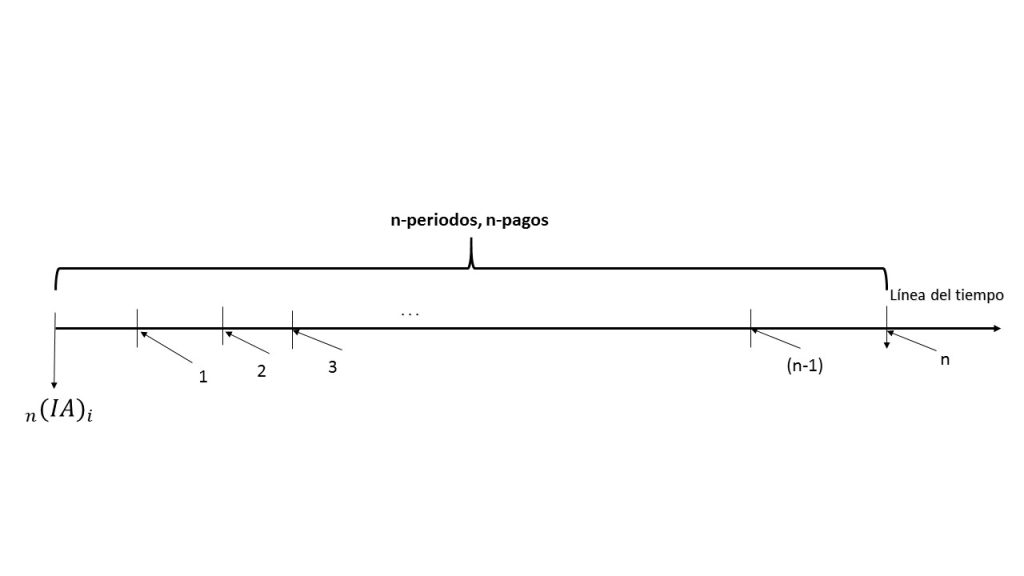
En la imagen, se muestra el comportamiento de una anualidad creciente ordinaria, en la que el capital (P), que se está manejando, así como el incremento (Q), se tomaron por igual a un peso. De dicho supuesto, la ecuación nos queda como sigue:
$P=Q=1$
$$\prescript{}{n}{\mathbf{IA}}_i=(1)\prescript{}{n}{\mathbf{A}}_i+(1)\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right)$$
de donde, sacando a $i$ como común denominador se tiene:
$$\prescript{}{n}{\mathbf{IA}}_i=\frac{i\prescript{}{n}{\mathbf{A}}_i+\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}.$$
Reagrupando términos:
$$\prescript{}{n}{\mathbf{IA}}_i=\frac{\prescript{}{n}{\mathbf{A}}_i+\frac{i(1-v^n)}{i}-nv^n}{i}.$$
Reduciendo y reordenando términos:
$$\prescript{}{n}{\mathbf{IA}}_i=\frac{\prescript{}{n}{\mathbf{A}}_i-v^n+1-nv^n}{i}.$$
Por último, se hace el recordatorio que:
$$\prescript{}{n-1}{\mathbf{A}}_i=\prescript{}{n}{\mathbf{A}}_i-v^n$$
sustituyendo el recordatorio en la ecuación que se venía desarrollando, se tiene por fin la expresión más sencilla para calcular el valor presente de una anualidad creciente ordinaria:
$$\prescript{}{n}{\mathbf{IA}}_i=\frac{\prescript{}{n-1}{\mathbf{A}}_i+1-nv^n}{i}.$$
De la misma forma que, con los modelos obtenidos anteriormente, haciendo despejes, se puede obtener cualquier variable que se utilice en ésa ecuación para conocer su valor numérico. Dentro del modelo que se acaba de obtener, es importante señalar que:
$P$ es el primer pago, no se le llamo $X$ para poder diferenciarlo de que los pagos dentro de las anualidades crecientes, van a ser diferentes cada uno de ellos.
Monto
Los montos en una anualidad creciente son denotados por:
$$\prescript{}{n}{\mathbf{SV}}_i.$$
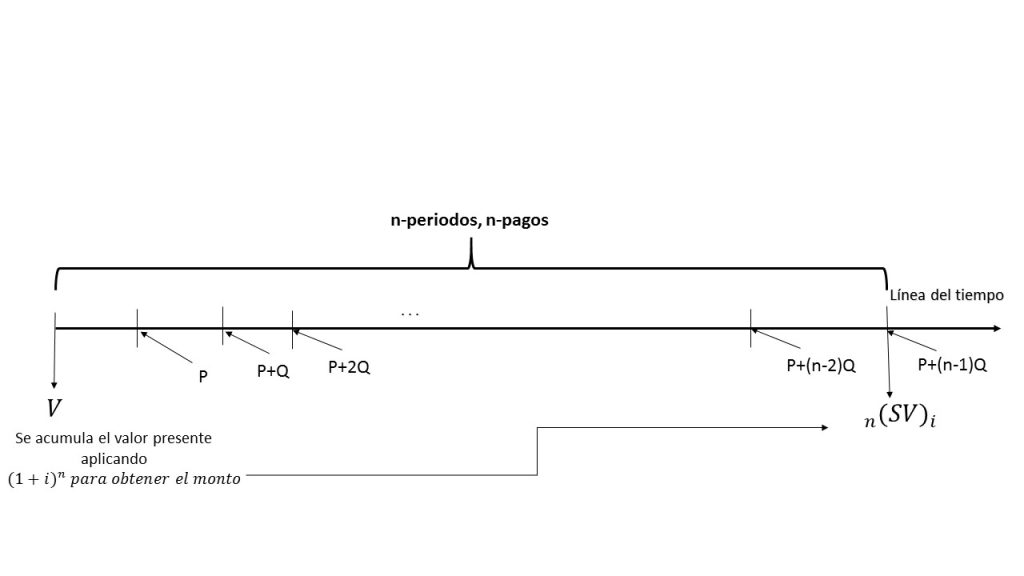
En la gráfica, se muestra el comportamiento del monto en una anualidad creciente, en la que se exhibe que el primer pago es denotado como $P$ y los pagos siguientes son representados por la letra $Q$, luego $2Q$, $3Q$, sucesivamente hasta llegar al valor $(n-1)Q$.
El monto, se calcula al tomar el valor presente de dicha anualidad, y se acumula durante $n$ periodos a la misma tasa de interés, esto se traduce en la siguiente expresión:
$$\prescript{}{n}{\mathbf{(SV)}}_i=\left(P\prescript{}{n}{\mathbf{A}}_i+Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right)\right)(1+i)^n.$$
Efectuando los productos indicados se tiene:
$$\prescript{}{n}{\mathbf{(SV)}}_i=P\prescript{}{n}{\mathbf{A}}_i(1+i)^n+Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i(1+i)^n-nv^n(1+i)^n}{i}\right).$$
Por otra parte, como:
$$\prescript{}{n}{\mathbf{(SV)}}_i=\prescript{}{n}{\mathbf{(A)}}_i(1+i)^n$$
además de que, $v^n=(1+i)^n$, y sustituyendo dicho valor en la ecuación anterior resulta:
$$\prescript{}{n}{\mathbf{(SV)}}_i=P\prescript{}{n}{\mathbf{S}}_i+Q\left(\frac{\prescript{}{n}{\mathbf{S}}_i-n}{i}\right).$$
Ésta, es la expresión más simplificada para obtener el monto de una anualidad creciente, con primer pago $P$ y pago siguiente $Q$ el cual se incrementa en cada periodo a una tasa de interés efectiva por periodo.
De forma semejante a como se ha venido haciendo, suponemos que $P=Q=1$, entonces se obtiene de forma sencilla la siguiente expresión:
$$\prescript{}{n}{\mathbf{(SV)}}_i=\frac{\prescript{}{n-1}{\mathbf{A}}_i+1-nv^n}{i}(1+i)^n$$
que corresponde a una anualidad creciente ordinaria, lo que es también equivalente a la siguiente expresión:
$$\prescript{}{n}{\mathbf{(SV)}}_i=\prescript{}{n}{\mathbf{S}}_i+\left(\frac{\prescript{}{n}{\mathbf{S}}_i-n}{i}\right).$$
Ejercicios resueltos
Ejercicio. Una empresa quiere modernizar su maquinaria, para ello se propone adquirir un crédito. El costo de la maquinaria asciende a un valor de \$1,500,000. Una vez adquirida e instalada, se estima que su producción se incrementará de la siguiente forma: \$30,000 fijos mensuales, con un crecimiento de \$10,000 para las siguientes mensualidades. Tomando en cuenta que la institución financiera que otorgó el préstamo, le da un plazo de un año para liquidar dicha deuda a una tasa de interés de 1.7% mensual, se desea saber ¿de cuánto será el crédito para solventar proyecto?
Solución
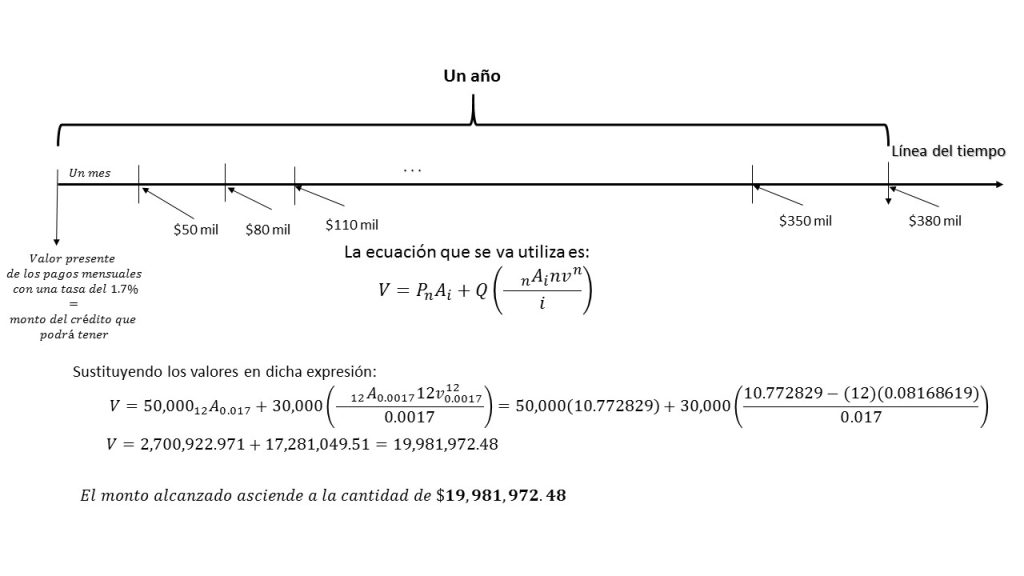
Como se debe encontrar el valor presente de una anualidad creciente, el cual es el camino que va a tomar la empresa para liquidar dicha deuda. Gráficamente se representa éste modelo en la siguiente imagen:
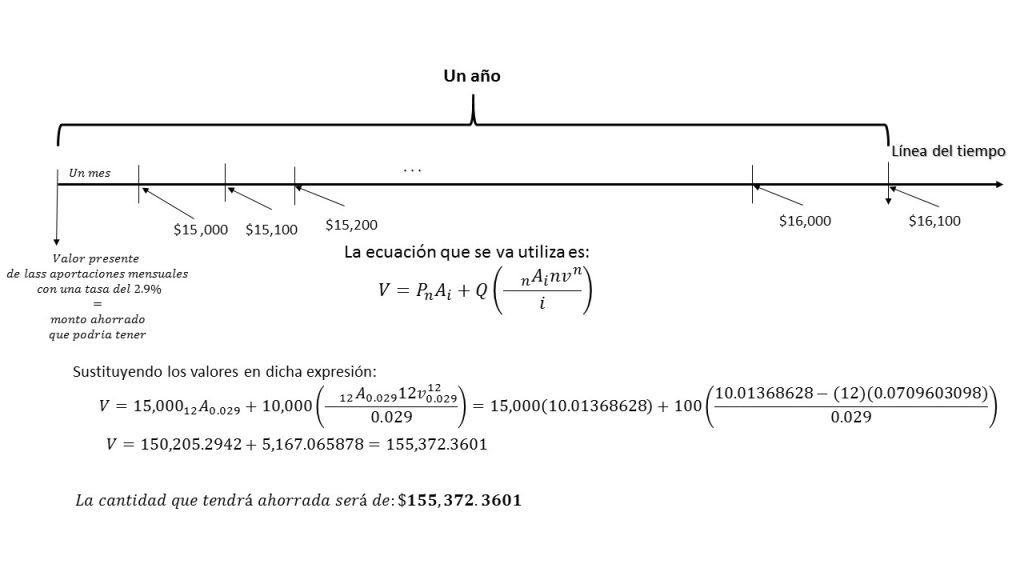
El señor Abel, quiere constituir una reserva para hacer frente a posibles emergencias que puedan presentarse, con la finalidad de no verse afectado en su economía cuando lleguen a ocurrir. Por tal motivo, quiere ahorrar su aguinaldo que recibió este año junto con sus prestaciones, las cuales en total ascienden a una cantidad de \$15 mil pesos, y planea hacer aportaciones por mil pesos, cantidad que quiere incrementar en \$100 pesos cada mes. Desea saber ¿cuánto dinero puede ahorrar?, si mantiene ésta forma de ahorro durante 1 año, y el banco en que mantiene sus ahorros le ofrece una tasa de interés del 2.9% mensual.
Más adelante…
Se continuará abordando el concepto de anualidad, ahora en su forma decreciente, en la que se analizará las situaciones en las que se utilizan, su comportamiento, la forma en que se calcula el monto, el valor presente, así como su construcción,
Entradas relacionadas
- Ir a Matemáticas Financieras
- Entrada anterior
- Entrada siguiente

Debes dar al inicio la definicion de cada letra, Asi pueden los demas facilmente traducir a por ejemplo:
El valor presente (V) de una anualidad creciente a una tasa de interes (i), con pagos 56 pagos (p) y asi sucesivamente. No se entiende la formula al final que valores se debe reemplazar
Hola Carclos. Gracias por el comentario. Se lo compartiré a Erick, quien ha estado trabajando en estas entradas de Matemáticas Financieras, para que lo tome en cuenta cuando haga revisiones.