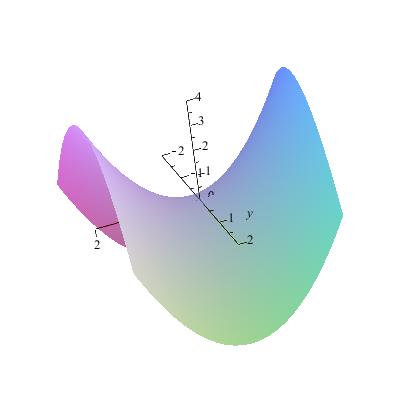Introducción
Los conjuntos de nivel proporcionan una representación visual de como la función toma ciertos valores en su dominio, mientras qu los límites nos permiten comprender el comportamiento de la función en puntos particulares o en el infinito. La relación entre ambos objetos puede verse como una descripción del comportamiento local y global de una función .
Funciones de $\mathbb{R}^{n}$ en $\mathbb{R}$
Definición 1 . Una función $f:A\subset\mathbb{R}^{n}\rightarrow \mathbb{R}$ es una función $f(x_{1},x_{2},…,x_{n})$ que asocia a cada n-ada ordenada $(x_{1},x_{2},…,x_{n})$ de $\mathbb{R}^{n}$ un número real $f(x_{1},x_{2},…,x_{n})$
Ejemplo. La función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+y^{2}$ asocia a dada pareja $(x,y)\in \mathbb{R}^{^{2}}$ el número real $x^{2}+y^{2}$.
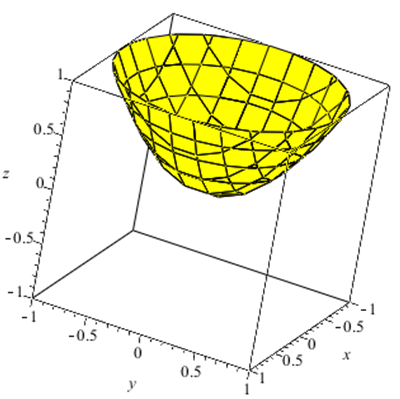
Ejemplo. La función $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ dada por $f(x,y,z)=\sqrt{1-x^{2}-y^{2}-z^{2}}$ asocia a dada terna $(x,y,z)\in \mathbb{R}^{^{3}}$ el número real $\sqrt{1-x^{2}-y^{2}-z^{2}}$
Definición 2. El dominio de una función $f:A\subset \mathbb{R}^{n}\rightarrow \mathbb{R}$ es el conjunto
$$Dom_{f}\left\{(x_{1},x_{2},…,x_{n})\in\mathbb{R}^{n}~|~f(x_{1},x_{2},…,x_{n})\in\mathbb{R}\right\}$$
Ejemplo. La función $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ dada por $f(x,y,z)=\sqrt{1-x^{2}-y^{2}-z^{2}}$ asocia a dada terna $(x,y,z)\in \mathbb{R}^{^{3}}$ el número real $\sqrt{1-x^{2}-y^{2}-z^{2}}$ tiene como dominio el conjunto
$$Dom_{f}=\left\{(x,y,z)\in\mathbb{R}^{3}~|~1-x^{2}-y^{2}-z^{2}\geq0 \right\}=\left\{(x,y,z)\in\mathbb{R}^{3}~|~1\geq x^{2}+y^{2}+z^{2}\right\}$$
Ejemplo La función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+y^{2}$ asocia a dada pareja $(x,y)\in \mathbb{R}^{^{2}}$ el número real $x^{2}+y^{2}$ en este caso el dominio es $\mathbb{R}^{2}$
Definición 3.$ El rango de una función $f:A\subset\mathbb{R}^{n}\rightarrow \mathbb{R}$ es el conjunto
$$Ran_{f}= \left\{f(x_{1},x_{2},…,x_{n})\in\mathbb{R}~|~(x_{1},x_{2},…,x_{n})\in\mathbb{R}^{n} \right\}$$
Ejemplo. La función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=\sqrt{1-x^{2}-y^{2}}$ asocia a dada pareja $(x,y)\in \mathbb{R}^{^{2}}$ el número real $\sqrt{1-x^{2}-y^{2}}$ en este caso el rango de la función es el conjunto
$$\left\{z\in\mathbb{R}~|~0\leq z\leq1 \right\}$$
Definición 4. La gráfica de una función $f:A\subset\mathbb{R}^{n}\rightarrow \mathbb{R}$ es el conjunto
$$Gra_{f}=\left\{(x_{1},x_{2},…,x_{n},f(x_{1},x_{2},…,x_{n}))\in\mathbb{R}^{n+1}~|~(x_{1},x_{2},…,x_{n})\in\mathbb{R}^{n}\right\}$$
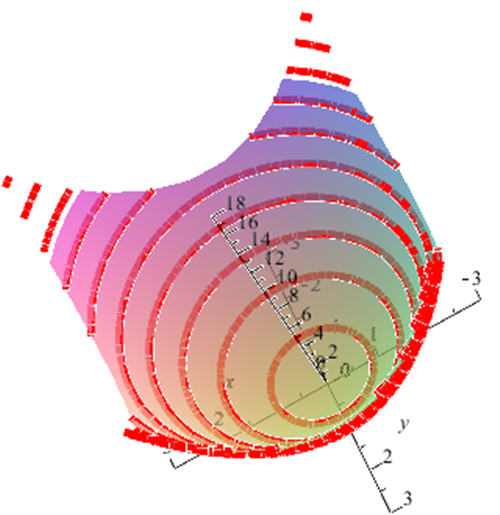
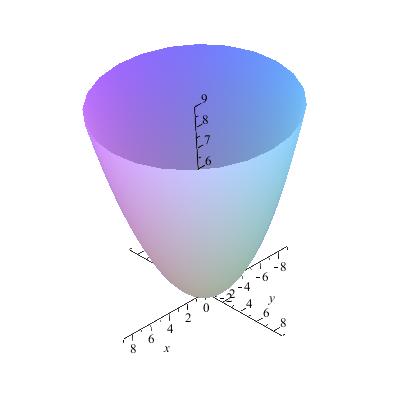
Ejemplo. La gráfica de la función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+y^{2}$ es un paraboloide cuyo aspecto es
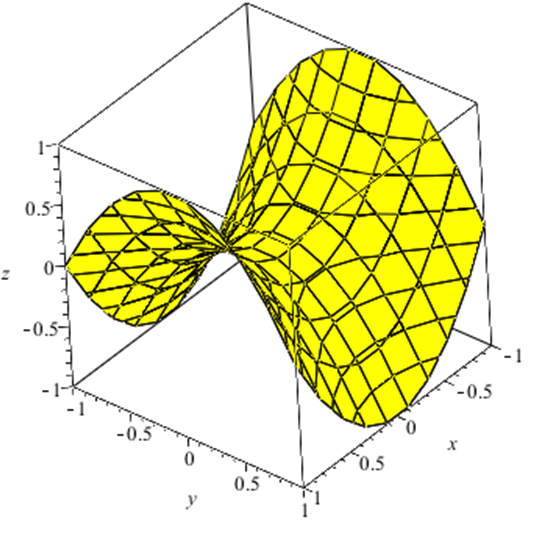
Ejemplo. La gráfica de la función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}-y^{2}$ es un paraboloide hiperbolico (silla de montar) cuyo aspecto es
Conjuntos de Nivel
Definición 5. Sea $f:\mathbb{R}^{n}\rightarrow\mathbb{R}$ y sea $c\in\mathbb{R}$. El conjunto de nivel del valor c se define como:
$$C_{N}=\left\{x\in\mathbb{R}^{n}~|~f(x)=c\right\}$$
Ejemplo. Describir el conjunto de nivel de la función $f(x,y)=x^{2}+y^{2}$
$Solución$ En este caso el conjnuto de nivel es$$C_{N}=\left\{(x,y)\in\mathbb{R}^{2}~|~x^{2}+y^{2}=c\right\}$$
geometricamente son circunferencias con centro el origen y radio $c$.
Ejemplo. Describir el conjunto de nivel de la función $f(x,y)=x^{2}-y^{2}$
Solución En este caso el conjnuto de nivel es$$C_{N}={(x,y)\in\mathbb{R}^{2}~|~x^{2}-y^{2}=c}$$
geometricamente son circunferencias con centro el origen y radio c
Ejemplo La función $f:\mathbb{R}^{2}\rightarrow \mathbb{R}$ dada por $f(x,y)=x^{2}+y^{2}$ tiene como gráfica el paraboloide de revolución $z=x^{2}+y^{2}$
Las curvas de nivel son: el vacio para $a<0$, y para $a>0$ es el conjunto $$\left\{(x,y)\in \mathbb{R}^{2}|x^{2}+y^{2}=a\right\}$$, es decir un círculo de radio $\sqrt{a}$ con centro en el origen
Ejemplo La función $f:\mathbb{R}^{2}\rightarrow \mathbb{R}$ dada por $f(x,y)=x^{2}-y^{2}$ tiene como gráfica el paraboloide hiperbolico $z=x^{2}-y^{2}$
Las curvas de nivel son: para $a=0\Rightarrow x^2-y^2=0$ par de rectas que se cortan en el origen, y para $a=1\Rightarrow x^2-y^2 =1$ es una hiperbola paralela al eje X que lo corta en $(\pm 1,0)$, para $a=-1\Rightarrow x^2-y^2=-1$ es una hiperbola paralela al eje Y y que lo corta en $(0,\pm 1)$
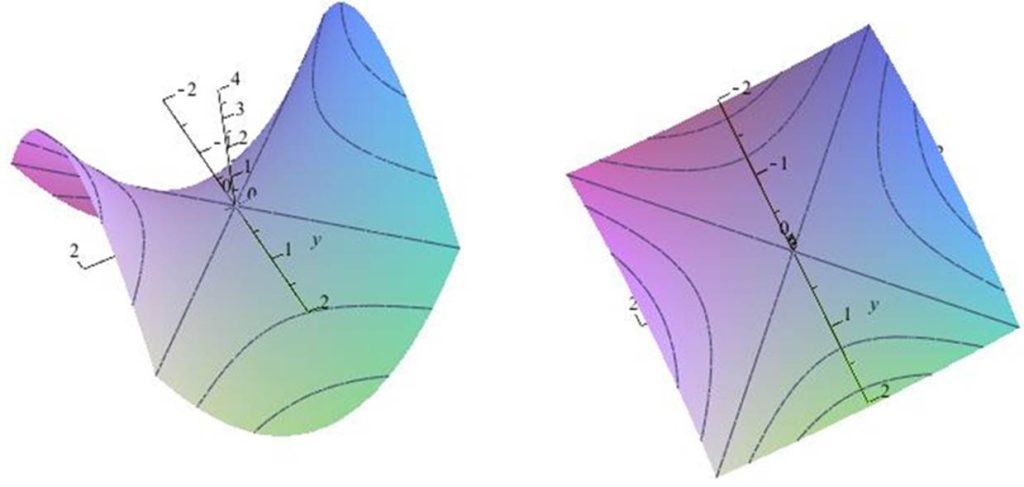
Ejemplo La función $f:\mathbb{R}^{3}\rightarrow \mathbb{R}$ dada por $f(x,y,z)=\sqrt{x^{2}+y^{2}+z^2}$ tiene el siguiente conjunto de nivel
$${(x,y,z)\in \mathbb{R}^{3}|\sqrt{x^2+y^2+z^2}=a}$$
Las superficies de nivel son: para $a=0\Rightarrow \sqrt{x^2+y^2+z^2}=0$ el origen, y para $a=1\Rightarrow \sqrt{x^2+y^2+z^2}=1$ es una esfera, $a=2\Rightarrow \sqrt{x^2+y^2+z^2}=2$ es una esfera
La función $f:\mathbb{R}^{3}\rightarrow \mathbb{R}$ dada por $f(x,y,z)=x^{2}-y^{2}+z^2$ tiene el siguiente conjunto de nivel
$$\left\{(x,y,z)\in \mathbb{R}^{3}|x^2-y^2+z^2=a\right\}$$
Las superficies de nivel son: para $a=0\Rightarrow x^2-y^2+z^2=1$ es un hiperboloide de un manto, y para $a=1\Rightarrow x^2-y^2+z^2=1$ es un hiperboloide de un manto, $a=2\Rightarrow \sqrt{x^2-y^2+z^2}=2$ es un hiperboloide de un manto
Límite de Funciones de $\mathbb{R}^{n} \rightarrow \mathbb{R}$
Sea $f:\Omega\subset\mathbb{R}^{n} \rightarrow \mathbb{R}$, y sea $x_{0}$ un punto de acumulación de $\Omega$. Se dice que $L\in\mathbb{R}$ es el límite de $f$ en
$x_{0}$, y se denota por: $$\displaystyle\lim_{x\rightarrow x_{0}}f(x)=L$$ Si dado $\varepsilon > 0$, existe $\delta > 0$ tal que $|f(x)-b|<\varepsilon$ cuando $x \in \Omega$, $0<|x-x_{0}|<\delta$
Observación: Es necesarío que $x_{0}$ sea punto de acumulacion de $\Omega$.
Usando la definición de límite, demostrar que:
$$\displaystyle\lim_{(x,y) \rightarrow (0,0)}\frac{x^{4}y^{2}}{(x^{2}+y^{2})^{2}}=0$$
Por demostrar, para todo $\varepsilon > 0$ existe $\delta > 0$ tal que $0 < |(x,y) – (0,0)| < \delta$ entonces $\displaystyle\left| \frac{x^{4}y^{2}}{(x^{2}+y^{2})^{2}} \right| < \varepsilon$
Demostración. Como $x^{2} \leq x^{2}+y^{2}$ entonces $x^{4} \leq (x^{2}+y^{2})^{2}$ entonces $\displaystyle\frac{1}{(x^{2}+y^{2})^{2}} \underset{(*)}{\leq} \displaystyle\frac{1}{x^{4}}$
$\therefore$ $\displaystyle\left|\frac{x^{4}y^{2}}{(x^{2}+y^{2})^{2}}\right| \underset{(*)}{\leq}
\displaystyle\left|\frac{x^{4}y^{2}}{x^{4}}\right| \leq |y^{2}|=y^{2}\leq (\sqrt{x^{2}+y^{2}})^{2} <
\delta^{2}$
$\therefore$ Si $\delta^{2}=\varepsilon$ entonces $\delta=\sqrt{\varepsilon}$
Más adelante
Relacionaremos el concepto de límite con el de derivada para funciones $f:\mathbb{R}^n \rightarrow \mathbb{R}$ escalares.
Tarea Moral
1.- Esboza las curvas de nivel y gráficas de las siguientes funciones
a) $f: \mathbb{R}^2 \rightarrow \mathbb{R}, (x,y) \rightarrow x-y+2$
b) $f: \mathbb{R}^2 \rightarrow \mathbb{R}, (x,y) \rightarrow x^2+4y^2$
2.- Describe el comportamiento conforme varia $c$ de la curva de nivel $f(x,y)=c$ para cada una de las siguientes funciones
a) $f(x,y)=x^2+y^2+1$
b) $f(x,y)=1-x^2-y^2$
3.- Traza la curva de nivel (en el plano $xy$) para las siguientes funciones.
a) $f(x,y)= 4-3x+2y, c=0,1,2,3,-1,-2,-3$
b) $f(x,y)=x/y, c=0,1,2,3,-1,-2,-3$
4.- Sea $f:\mathbb{R}^2 \rightarrow \mathbb{R}. (x,y) \rightarrow x^2+y^2+2$ calcular $\displaystyle\lim_{(x,y) \rightarrow (0,1)} f(x,y)$
5.- Sea $f:A \subset \mathbb{R}^n \rightarrow \mathbb{R}$, $x_0$ un elemento o punto fronrtera de $A \in \mathbb{R}^n$ y $b\in\mathbb{R}$ demuestra que si
$\displaystyle\lim_{x \rightarrow x_0}f(x)=b$ entonces $$c \displaystyle\lim_{x \rightarrow x_0}f(x)=cb$$
Enlaces
Calculadora para curvas de nivel de funciones de $\mathbb{R}^2 \rightarrow \mathbb{R}$