Introducción

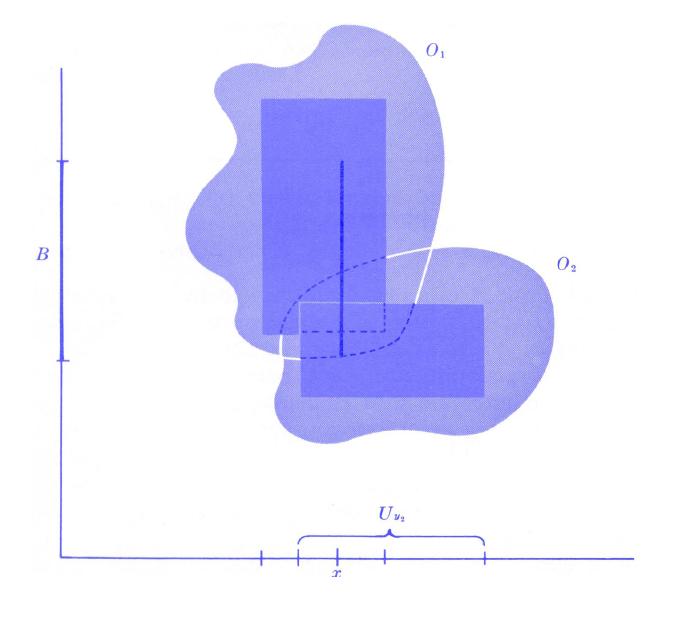
Análogamente al cálculo univariable, una función $f(x,y)$ es continua en un punto $(a,b)$ si se cumplen las siguientes condiciones: la función está definida en $(a,b)$, es decir $f(a,b)$ existe, el límite existe y además coincide con el valor de la función, sin embargo, en varias variables hay varias maneras de acercarse a un punto, por ejemplo: a lo largo del eje $x$, (manteniendo $y$ fijo); a lo largo del eje $y$, (manteniendo $x$ fijo), a lo largo de líneas diagonales; curvas o incluso camimnos extraños. Si el límite cambia dependiendo de la dirección de aproximación, la función no es continua en ese punto.

Proposición 1 Sea $f:\mathbb{R}^{2}\rightarrow \mathbb{R}$ tal que $$\lim_{(x,y)\rightarrow (a,b)}f(x,y)=L$$
Entonces para una función real y continua $g$ definida en un entorno da $a$ tal que $$\lim_{x\rightarrow a}g(x)=b$$ se tiene que $$\lim_{x\rightarrow a}f(x,g(x))=L$$

Demostración. Por la existencia del límite doble, dado $\epsilon>0$ existe un $\delta>0$, tal que $$|(x,y)-(a,b)|<\delta \Rightarrow |f(x,y)-L|<\epsilon.$$ Ahora $$\lim_{x\rightarrow a}g(x)=b$$ quiere decir que dado $\delta>0$ existe $\sigma>0$, con $0<\sigma<\delta$ tal que: $$|x-a|<\sigma \Rightarrow |g(x)-b|<\delta.$$ Por
tanto, si $|x-a|<\sigma$, se tiene que $|(x,g(x))-(a,b)|<\delta.$ Con lo cual, $$|f(x,g(x))-L|<\epsilon$$ $\square$

Ejemplo: Determinar si existe, el límite de la función definida por

$f(x,y)= \left\{\begin{array}{lcc} \frac{x^{2}y}{x^{2}+y^{2}}&(x,y)\neq (0,0)\\ \\0&(x,y)=(0,0)\end{array}\right.$

Para determinar su límite podemos acercarnos por trayectorias (funciones continuas) al origen.

Pongamos $y=g(x)=0$ se tiene entonces que

$$\lim_{(x,y)\rightarrow(0,0)}f(x,y)=\lim_{(x,y)\rightarrow(0,0)}f(x,g(x))=\lim_{(x,y)\rightarrow(0,0)}f(x,0)=\lim_{x\rightarrow0}\frac{x^{2}0}{x^{2}+0^{2}}=0$$
Pongamos ahora $y=g(x)=x$ se tiene entonces que
$$\lim_{(x,y)\rightarrow(0,0)}f(x,y)=\lim_{(x,y)\rightarrow(0,0)}f(x,g(x))=\lim_{(x,x)\rightarrow(0,0)}f(x,x)=\lim_{x\rightarrow0}\frac{x^{2}x}{x^{2}+x^{2}}=\lim_{x\rightarrow0}\frac{x^{3}}{2x^{2}}=0$$
Lo anterior nos dice que si existe el límite, éste tendría que ser 0, para comprobarlo usaremos la definición, se tiene entonces que debemos hallar un $\delta>0$ tal que
$\left|\frac{x^{2}y}{x^{2}+y^{2}}\right|<\epsilon$ siempre que $|(x,y)-(0,0)|<\delta$. Observamos que
$$\left|\frac{x^{2}y}{x^{2}+y^{2}}\right|=\frac{|x^{2}||y|}{|x^{2}+y^{2}|}=\frac{|x|^{2}|y|}{|x^{2}+y^{2}|}\leq
\frac{|\overline{x}|^{2}|\overline{x}|}{|\overline{x}|^{2}}=|\overline{x}|<\delta.$$
$\therefore$ podemos tomar $\delta=\epsilon$

Ejemplo: Determinar si existe, el límite de la función definida por

Para determinar su límite podemos acercarnos por trayectorias (funciones continuas) al origen.

Pongamos $y=g(x)=x$ se tiene entonces que

$$\lim_{(x,y)\rightarrow(0,0)}f(x,y)=\lim_{(x,y)\rightarrow(0,0)}f(x,g(x))=\lim_{(x,x)\rightarrow(0,0)}f(x,x)=\lim_{x\rightarrow0}\frac{x^{2}}{x^{2}+x^{2}}=\frac{1}{2}$$

Pongamos $y=g(x)=0$ se tiene entonces que

$$\lim_{(x,y)\rightarrow(0,0)}f(x,y)=\lim_{(x,y)\rightarrow(0,0)}f(x,g(x))=\lim_{(x,0)\rightarrow(0,0)}f(x,0)=\lim_{x\rightarrow0}\frac{x (0)}{x^{2}+0^{2}}=0$$

como $\frac{1}{2}\neq 0$ entonces $\cancel{\exists}$ el límite de la función.

Continuidad de Funciones de $\mathbb{R}^{n} \rightarrow \mathbb{R}$

Definición 1. Sea $f:\Omega\subset\mathbb{R}^{n} \rightarrow \mathbb{R}$, y sea $x_{0}$ un punto de acumulación de $\Omega$.Se dice que $f(x_{0})\in\mathbb{R}$ es el límite de $f$ en $x_{0}$, y se denota por: $$\displaystyle\lim_{x\rightarrow x_{0}}f(x)=f(x_{0})$$ Si dado $\varepsilon > 0$, existe $\delta > 0$ tal que $|f(x)-f(x_{0})|<\varepsilon$ cuando $x \in \Omega$, $0<|x-x_{0}|<\delta$

Ejemplo: Demostrar la continuidad en $\mathbb{R}^2$ de la función $f(x,y)=xy$.

p.d. Dado $\epsilon>0$ $\exists$ $\delta>0$ tal que $|xy-ab|\leq \epsilon$ siempre que $0<|x-a|<\delta_1$ y $0<|y-b|\leq \delta_2$ tenemos que:

$|xy-ab|
=|xy-xb+xb-ab|
\leq |x(y-b)|+|b(x-a)|
\leq \left(|x-a|+|a|\right)|y-b|+|b||x-a|\leq \left(\delta+|a|\right)\delta+|b|\delta
=\delta\underset{\underset {\text{Esta la podemos acotar}}{\searrow\ \ \ \ \ \ \ \ \ \ \ \
}}{\left(\left(\delta+|a|\right)+|b|\right)}$

Si $\delta=1$ tenemos que $\delta(1+|a|+|b|)$ y asi tomamos

$$\delta=mín \left\{ 1 , \frac{\epsilon}{1+|a|+|b|}\right\}$$

Diferenciación de funciones $\mathbb{R}^{n}\rightarrow\mathbb{R}$

Sea $f:A \subseteq\mathbb{R}^{n}\rightarrow \mathbb{R}$ y $\overline{a}=(a_{1},\ldots,a_{n})\epsilon$ $A$. Se define la derivada pacial $i$-esima en $\overline{a}$ denotada $f_{x}(\overline{a})$, $D_{x}f(\bar{a})$ ó $\displaystyle\frac{\partial f}{\partial x}(\bar{a})$ de la forma $$f_{x}=\displaystyle\lim_{h \rightarrow 0}\frac{f(a_{1},\ldots,a_{i}+h,\ldots.a_{n})-f(\bar{a})}{h}=\displaystyle\lim_{h \rightarrow 0}\frac{f(a+he_{i})-f(a)}{h}$$ siendo $\bar{e}_{i}=(0,\ldots,\underset{i-esimo}{1},\ldots,0)$.

Si $n=2$ existen 2 derivadas parciales.

Sea $\bar{a}=(x_{0},y_{0})$ un punto del interior del dominio de $f:A \subseteq\mathbb{R}^{2}\rightarrow \mathbb{R}$ las derivas parciales de $f$ en el punto $\bar{a}$ denotada respectivamente por $f_{x}(x_{0},y_{0})$, $f_{y}(x_{0},y_{0})$
son:

$$f_{x}(x_{0},y_{0})=\displaystyle\lim_{h \rightarrow 0}\frac{f(x_{0}+h,y_{0})-f(x_{0},y_{0})}{h}$$
$$f_{y}(x_{0},y_{0})=\displaystyle\lim_{k \rightarrow 0}\frac{f(x_{0},y_{0}+k)-f(x_{0},y_{0})}{k}$$

Ejemplo. Si $f(x,y)=x^{2}+x+1$ entonces
$f_{x}(0,0)=1$ ya que $f_{x}=\displaystyle\lim_{h \rightarrow 0}\frac{f(0+h,0)-f(0,0)}{h}=
\displaystyle\lim_{h \rightarrow 0}\frac{h^{2}+h+1-1}{h}=\displaystyle\lim_{h \rightarrow 0}\frac{h(h+1)}{h}=
\displaystyle\lim_{h \rightarrow 0}h+1 = 1$ y $f_{y}=\displaystyle\lim_{k \rightarrow 0}\frac{f(0,0+k)-f(0,0)}{k}=
\displaystyle\lim_{k \rightarrow 0}\frac{1-1}{k}=0$

Ejemplo. Si $f(x,y)=x^{2}+x+1$ entonces $f_{x}(0,0)=1$ ya que

$f_{x}=\displaystyle\lim_{h \rightarrow 0}\frac{f(0+h,0)-f(0,0)}{h}=
\displaystyle\lim_{h \rightarrow 0}\frac{h^{2}+h+1-1}{h}=\displaystyle\lim_{h \rightarrow 0}\frac{h(h+1)}{h}= \displaystyle\lim_{h \rightarrow 0}h+1 = 1$ y $f_{y}=\displaystyle\lim_{k \rightarrow 0}\frac{f(0,0+k)-f(0,0)}{k}= \displaystyle\lim_{k \rightarrow 0}\frac{1-1}{k}=0$

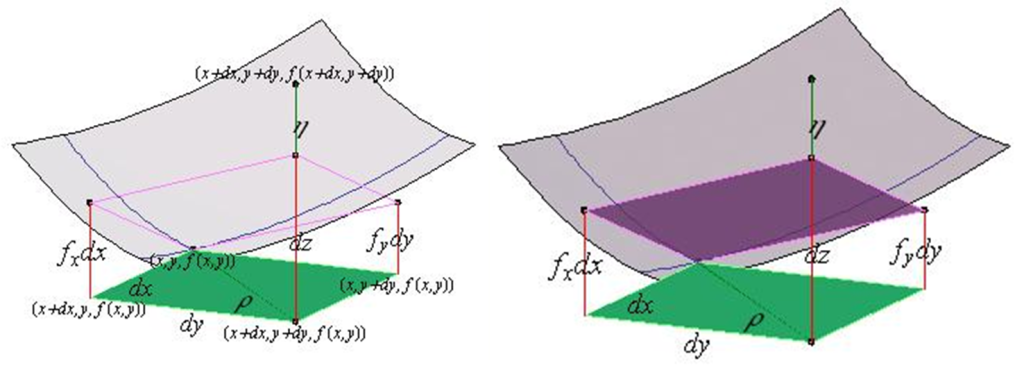
Observación: La derivada parcial en un punto de una función de varias variables en la derivada de la función de una variable, obtenida haciendo constante todas las variables, menos una. en consecuencia se pueden aplicar con esta interpretación, las reglas de derivación en una variable.

Las derivadas parciales en el punto $(x_{0},y_{0})$ de la función $z=f(x,y)$ representa la pendiente de las curvas intersección $C_{1}$ y $C_{2}$ de la superficie $z=f(x,y)$ con los planos $y=y_{0}$, $x=x_{0}$ respectivamente

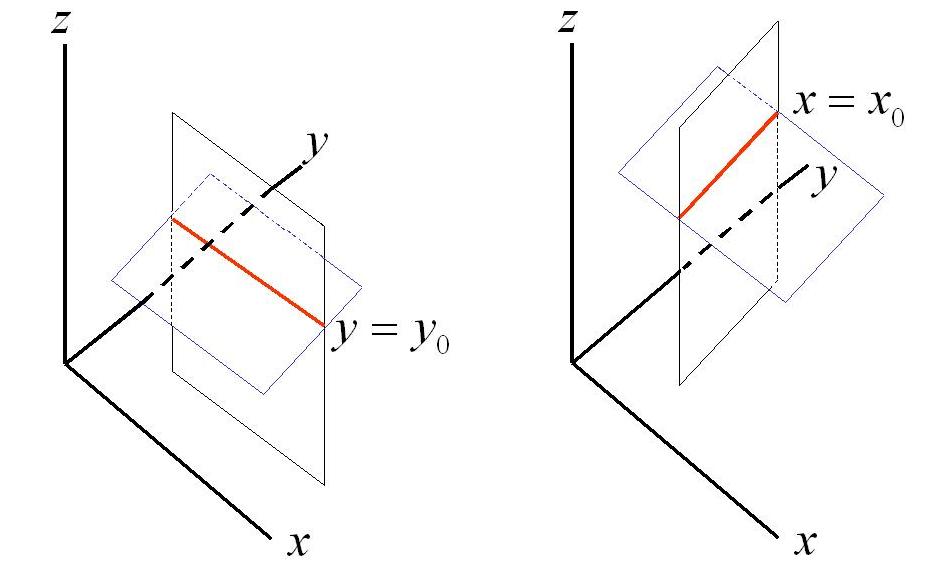
Ejemplo. Calcular las derivadas parciales

$a)$ $f(x,y)=a\arcsin(x-y)$

$b)$ $f(t,u)=\displaystyle\frac{\cos(2tu)}{t^{2}+u^{2}}$

$c)$ $f(x,y,z)=\displaystyle\frac{xyz}{x^{2}+y^{2}+z^{2}}$

$d)$ $f(x,y)=\displaystyle\int_{0}^{\sqrt{xy}}e^{-t^{2}}dt \qquad x>0, \, y>0$

Solución.

$a)$ $f_{x}=\displaystyle\frac{x}{\sqrt{1-(x-y)^{2}}}+ \arcsin(x-y)$

$f_{y}=\displaystyle\frac{-x}{\sqrt{1-(x-y)^{2}}}$

$b)$ $f_{t}=\displaystyle\frac{-(t^{2}+u^{2})\sin(2tu)\cdot2u-\cos(2tu)2t}{(t^{2}+u^{2})^{2}}$

$f_{u}=\displaystyle\frac{(t^{2}+u^{2})-\sin(2tu)2u-\cos(2tu)2u}{(t^{2}+u^{2})^{2}}$

$c)$ $f_{x}=\displaystyle\frac{(x^{2}+y^{2}+z^{2})yz-xyz(2x)}{(x^{2}+y^{2}+z^{2})^{2}}$

$f_{y}=\displaystyle\frac{(x^{2}+y^{2}+z^{2})xz-xyz(2y)}{(x^{2}+y^{2}+z^{2})^{2}}$

$f_{z}=\displaystyle\frac{(x^{2}+y^{2}+z^{2})xy-xyz(2z)}{(x^{2}+y^{2}+z^{2})^{2}}$

$d)$ $f_{x}=\displaystyle e^{-xy}\frac{y}{2\sqrt{xy}}$

$f_{y}=\displaystyle e^{-xy}\frac{x}{2\sqrt{xy}}$

Más adelante

Definiremos la derivada parcial y notaremos como es similar a la derivada ordinaria a una dimensión evaluando un límite de un cociente que va incrementando en una direccion.

Tarea Moral

1.- Sea $f: \mathbb{R}^2 \rightarrow \mathbb{R}$, $(x,y) \rightarrow x^2 + y^2 + 5$, calcular el límite $\lim_{(x,y)\rightarrow(0,1)}f(x,y)$

2.- Mostrar que $f: \mathbb{R}^2 \rightarrow \mathbb{R}^2$, $(x,y) \rightarrow (x^2y,(y+x^3)/(1+x^2))$

3.- Considera la función $f(x,y)=\dfrac{sen(x^2+y^2)}{x^2+y^2}$ aunque $f$ no esté definida en $(0,0)$ determina si la función tiende a algún número cuando $(x,y)$ tiende a $(0,0)$

4.-Muestra que $f:\mathbb{R}^n \rightarrow \mathbb{R}^m$ es continua en todos los puntos si y sólo si la imagen inversa de todo abierto es abierta.

5.- Calcula las siguientes derivadas parciales :

$f(x,y)= e^{xy}log(x^2+y^2)$

$f(x,y)=\dfrac{2xy}{(x^2+y^2)^2}$

Enlaces

Introducción

El criterio de Cauchy es una herramienta bastante útil para demostrar convergencia en conjuntos compactos porque en estos conjuntos toda sucesión de Cauchy converge necesariamente.

Definición. Sea ${\overline{x_{k}}}$ una sucesión de puntos de $\mathbb{R}^{n}$. Se dice que ${\overline{x_{k}}}$ es una sucesión de Cauchy si dado $\epsilon>0$ $\exists N_{0}\in \mathbb{N}$ tal que $|\overline{x_{k}}-\overline{x_{l}}|<\epsilon$ $\forall k,l\geq N_{0}$

Teorema 1. Una sucesión $\overline{x_{k}}\in \mathbb{R}^{n}$ es convergente si y solo si cumple el criterio de Cauchy

Demostración. $\Rightarrow$ Suponemos que ${\overline{x_{k}}}\rightarrow \overline{x}$ $\therefore$ $|\overline{x_{k}}-\overline{x}|<\epsilon$ $\forall k>N_{0}$. Se tiene entonces que $$|\overline{x_{k}}-\overline{x_{l}}|=|\overline{x_{k}}-\overline{x}+\overline{x}-\overline{x_{l}}|\leq |\overline{x_{k}}-\overline{x}|+|\overline{x}-\overline{x_{l}}|<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon$$ $\forall k,l>N_{0}$ $\therefore$ ${\overline{x_{k}}}$

$\Leftarrow$ Supongamos que ${\overline{x_{k}}}$ cumple la condición de Cauchy por tanto se tiene que: $$|\overline{x_{k}}-\overline{x_{l}}|<\epsilon\Rightarrow |x_{i,k}-x_{i,l}|<\epsilon\quad \forall i\Rightarrow {x_{i,k}}\quad cumple\quad Cauchy$$ $\therefore$ $x_{i,k}$ es convergente $\forall i$ $\therefore$ ${\overline{x_{k}}}$ es convergente. $\square$

Teorema 2. (Bolzano-Wierstrass) Toda sucesión $\overline{x_{k}}$ en $\mathbb{R}^{n}$ acotada tiene un punto limite. Dicho de otro modo, toda sucesión en $\mathbb{R}^{n}$ tiene una subsucesión convergente

Demostración. Sea $\overline{x_{k}}$ en $\mathbb{R}^{n}$ suponiendo $\overline{x_{k}}$ es acotada, entonces cada $x_{i,k}$ es acotada $\therefore$ según el teorema de Bolzano-Wierstrass para sucesiones en $\mathbb{R}$, ${x_{i,k}}$ tiene una subsucesión convergente $\alpha_{i,k}$ la cual es una sucesión convergente, $\therefore$ podemos formar la sucesiòn $\overline{x_{\alpha,k}}={x_{\alpha,1,k},x_{\alpha,2,k},…,x_{\alpha,n,k}}$ la cual es una sucesión convergente, pero $\overline{x_{\alpha,k}}$ es subsucesión de $\overline{x_{k}}$ $\therefore$ $\overline{x_{k}}$ tiene una subsucesión convergente. $\square$

Criterio de Convergencia de Cauchy

Una colección $g$ de conjuntos abiertos cuya unión contiene a $K$ con frecuencia se llama cubierta de $K$. De modo que el requisito para que $K$ sea compacto es que toda cubierta $g$ de $K$ se pueda sustituir por una cubierta finita $g$ de $K$.

Ejemplo. Sea $k={x_{1},x_{2},…,x_{m}}$ un subconjunto finito de $\mathbb{R}^{n}$ si $G={G_{\alpha}}$ es una colección de abiertos tal que $k\subset{G_{\alpha}}$ y si todo punto de k pertenece a algún subconjunto de ${G_{\alpha}}$ entonces cuando más m subconjuntos de ${G_{\alpha}}\supset k$ $\therefore$ k es un subconjunto compacto de $\mathbb{R}^{n}$.

Ejemplo. Considere al subconjunto $H=\left\{x\in \mathbb{R}| x\geq0\right\}$. Sea $G_{n}=(-1,n)$ $n\in \mathbb{N}$ de tal manera que ${G_{n}| n\in \mathbb{N}}$ sea una colección de subconjuntos abiertos de $\mathbb{R}$ cuya union contenga a $H$. Si ${G_{n_{1}}, G_{n_{2}},…,G_{n_{k}}}$ es una subcolección finita de ${G_{n}|n\in\mathbb{N}}$. Sea $M=sup\left\{n_{1},n_{2},…,n_{k}\right\}$ de tal manera que $G_{n_{j}} \subset G_{n_{k}}$ de aquí deducimos que $G_{M}$ es la unión de
${G_{n_{1}}, G_{n_{2}},…,G_{n_{k}}}$. Sin embargo el número real $M$ no pertenece a $G_{M}$ y por lo tanto no pertenece a $\bigcup_{j=1}^{k}G_{n_{j}}$. En consecuencia, ninguna unión finita de ${G_{n}|n\in\mathbb{N}}$ puede contener a $H$.$\therefore$ $H$ no es compacto.

Ejemplo. Demuestrese que todo intervalo cerrado $[a, b]$ de $\mathbb{R}$ es compacto.
Demostración. Supongamos un recubrimiento abierto $[a, b]$ tal que no admite subrecubrimiento finito. Entonces tampoco existe un subrecubrimiento finito para

$[a, c]$ $[c; b]$ con $c$ punto medio. Sea $[a_1, b_1] = [a, c]$ el intervalo para el cual no existe el subrecubrimiento finito.

Sea $[a_1, b_1] = [a, c]$ el intervalo para el cual no existe el subrecubrimiento finito.

Sea $p$ el punto de intersección y sea $U$ el recubrimiento que contiene a $p$ y sea $[p-\varepsilon,p+\varepsilon]\subset U$. Entonces existe $r \in \mathbb{N}$ tal que $\forall n > r$,$\frac{b-a}{2^n} < \varepsilon$ y $\forall \, n\geq r$ $[a_n,b_n]\subset U \underset{\circ}{\bigtriangledown}$ ya que ningun $[a_k, b_k]$ admitía un subrecubrimiento finito.

Ejemplo. Sea $H=(0,1)$ en $\mathbb{R}$. Si $G_{n}={\frac{1}{n},1-\frac{1}{n}}$ para $n>0$ entonces la colección${G_{n_{1}},G_{n_{2}},…,G_{n_{k}}}$ es una subcolección finita de ${G_{n}| n>2}$. Sea $M=sup{n_{1},…,n_{k}}$ de tal manera que $G_{n_{j}} \subset G_{M}$ se ifiere que $G_{M}$ es la unión de ${G_{n_{1}},G_{n_{2}},…,G_{n_{k}}}$ sin embargo el número real $\frac{1}{m}$ pertenece a $H$ pero no pertenece a $G_{M}$ $\therefore$ ninguna subcolecciónfinita de $\left\{G_{n}~|~ n>2\right\}$ puede formar una subcolección finita para $H$ $\therefore$ $H$ no es compacto.

Compactos por Sucesiones

Teorema 3. Sea $A\subset \mathbb{R}^{n}$ tal que para todo recubrimiento abierto $\left\{A_{i}\right\}_{i\in I}$ admite un subrecubrimiento finito es decir $\displaystyle{A\subset \bigcup_{i}^{n}A_{i}}$ entonces toda sucesión de puntos de $A$ tiene una subsucesión convergente hacia un punto que pertenece a $A$

Demostración. Supongamos que exite una sucesión $\overline{x}{n}\in A$ que no tuviera una subsucesión convergente (en este caso $\overline{x}_{n}$ tiene infinitos elementos). Sea $\overline{x}\in A$ como $\lim_{n\rightarrow\infty}\overline{x}{n}\neq \overline{x}$, existe $\delta{x}>0$ tal que en la bola abierta $B(\overline{x},\delta_{x})$ solo hay a lo más un número finito de elementos de $\overline{x}_{n}$. Entonces la familia de abiertos ${B(\overline{x},\delta{x})}$ es un recubrimiento abierto de A; por hipótesis este recubrimiento admite un subrecubrimiento finito $A_{x_{1}},A_{x_{2}},…,A_{x_{n}}$ de estos abiertos. Por lo tanto los infinitos elementos de $\overline{x}_{n}$ que estan en $A$ pueden ser cubiertos por un número finito de conjuntos abiertos $\underset{\circ}{\bigtriangledown}$ pues cada $A{x_{i}}$ cubre a lo mas un número finito de elementos de $A$.

Teorema 4. Si toda sucesión de puntos de $A$ tiene una subsucesión convergente hacia un punto que pertenece a $A$ entonces $A$ es cerrado y acotado.

Demostración. A es cerrado. Sea $\overline{a}\in\mathbb{R}^{n}$ tal que $\overline{a}\in \partial A$ vamos a ver que $\overline{a}\in A$. Como $\overline{a}\in \partial A$ entonces $\forall~r>0$ $B(\overline{a},r)\bigcap A\neq \emptyset$ consideremos ahora $r=\frac{1}{n}$ y en cada bola abierta $\displaystyle{(\overline{a},\frac{1}{n}}$ hay algún punto de $A$ al que podemos llamar $\overline{x}{n}$ de esta manera construimos una sucesión de puntos de $A$ que convergen a $\overline{a}$ por lo tanto por hipótesis $\overline{a}\in A$ por tanto $A$ es cerrado.

A es acotado. Si $A$ no fuera acotado, existiria una sucesión $\overline{x}_{n}$ de puntos de $A$ tal que $\lim_{n\rightarrow\infty}\overline{x}_{n}=\infty$ y este límite no estaría en $A$ $\underset{\circ}{\bigtriangledown}$ por tanto $A$ es acotado.

Teorema. Heine-Borel. Todo subconjunto cerrado y acotado es compacto.

$1.-$ $K$ compacto implica que $K$ es cerrado.

Demostración. Sea $\bar{x} \in K^c$ y sea $G_m =\left\{y \in \mathbb{R}^n | |y-x | > \frac{1}{m}, m \in \mathbb{N}\right\}$ entonces $y \in Ext B(\bar{x}, \frac{1}{m})$ cada $G_m$ es abierta, la unión de todas las $G_m$ consta de todos los puntos de $\mathbb{R}^n$ excepto $x$. Dado que $x \in K$ cada punto de $K$ pertenece a algún $G_m$. Debido a la compacidad de $K$, se infiere que existe $M \in \mathbb{N}$ tal que $K \subset \bigcup_1^m G_i$. Dado que los conjuntos $G_m$ incrementan con $m$, $K \subset G_m$ de donde la vecindad ${z \in \mathbb{R}^n | |z-x| < \frac{1}{m}}$ no intercepta a $K$ demostrando que $K^c$ es abierto $\therefore$ $K$ es cerrado.

$2.-$ $K$ compacto implica que $K$ es acotado.

Demostración. Sea $H_m = \left\{ x \in \mathbb{R}^n | \left\| x\right\| < m\right\}$ todo el espacio $\mathbb{R}^n$ y por tanto $K$ está contenido en la unión de los conjuntos crecientes, $H_m$ $m\in \mathbb{N}$. Dado que $K$ es compacto existe $M \in \mathbb{N}$ tal que $K \subset H_m$ por lo que $K$ esta acotado.

Para completar la demostración de este teorema se necesita probar que si $K$ es un subconjunto cerrado y acotado contenido en la unión de una colección $g {G_{\alpha}}$
de conjuntos abiertos en $\mathbb{R}^n$, entonces está contenido en la unión de
algún número finito de conjuntos de $g$.

Dado que $K$ esta acotado, encontramos un punto de acumulación de $K$, como $K$ es cerrado $y \in K$ y esta en alguna celda abierta, por lo tanto existe $\varepsilon > 0$ tal que para cada $w$ con $|y -w| < \varepsilon $ en la celda abierta y si suponemos que $g ={G_{\alpha}}$ no admite un subrecubrimiento finito llegamos a una contradicción.

Teorema 6. Si $S$ es un conjunto cerrado y acotado en $\mathbb{R}^{n}$ entonces $S$ es compacto por sucesiones

Demostración. Suponga que $S$ es cerrado y acotado, sea ${x_{k}}$ una sucesión de puntos de $S$, se tiene entonces que $S$ es acotada y por el teorema de Bolzano- Weierstrass ${x_{k}}$ tiene una subsucesión convergente ${x_{k_{\alpha}}}$ tal que $x_{k_{\alpha}}\rightarrow x$ y como $S$ es cerrado $x\in S$. $\square$

Más adelante

En la siguiente sección estudiaremos el cálculo diferencial en las funciones reales ($\mathbb{R}^n\rightarrow \mathbb{R}$). Notaremos como los conceptos definidos en esta sección son necesarios para la noción de derivada, entre otros temas

Tarea Moral

1.-Sea $\left\{ \widehat{x}_{k} =( x^{(1)}_k, …, x{^(n)}_k) \right\}$ una sucesión en $\mathbb{R}^n$. Pruebe que $\left\{\widehat{x}_{k}\right\}$ está acotada si y sólo si $\left\{x^{(i)}_k\right\}$ está acotada para cada $i \in {1,…,n}$.

2.- Pruebe que si $\left\{ \widehat{x}_{k} \right\}$ es una sucesión de Cauchy en $\mathbb{R}^n$, entonces cualquier subsucesión también lo es.

3.- Sea $\left\{ \widehat{x}_{k} \right\}$ una sucesión de Cauchy en $\mathbb{R}^n$, prueba directamente de la definición la sucesión $\left\{ \widehat{x}_{k} \right\}$ está acotada.

4.- Sea $k \subset \mathbb{R}^n$. Prueba que el conjunto $K$ es compacto si y sólo si toda sucesión $\left\{ \widehat{x}_{k} \right\} \subset K$ tiene una subsucesión que converge a un punto $\widehat{x}_{0} \in K$ .

5.- Prueba que $\mathbb{R}^n$ no es compacto.

Enlaces

Puntos Interiores y Cerradura de un Conjunto

Proposición. Para todo subconjunto $A$ de $\mathbb{R}^n$ se tiene:

$(1)$ $int(A)\subset A$

Demostración. Si $\bar{a}\in int(A)$ $\exists$ $r>0$ tal que $B(\bar{a},r)\subset A$ $\therefore$ $int(A) \subset A$

$(2)$ $A\subset\bar{A}$

Demostración. Si $\bar{a}\in A$ $\forall$ $B(\bar{a},r)$ se tiene que $B(\bar{a},r)\cap A\neq\emptyset$ $\therefore$ $A\subset\bar{A}$

Lema. Sea $A$ un subconjunto de $\mathbb{R}^n$

(1) Si $v\subset A$ y $v$ es abierto entonces $v\subset A^o$

Demostración. Sea $\bar{x}\in v$, como $v$ es abierto $\exists$ $r>0$ tal que $B(\bar{x},r)\subset v$ y como $v\subset A$ entonces $B(\bar{x},r)\subset A$ esto significa que $\bar{x}$ es un punto interior de $A$ es decir $\bar{x}\in A$.

(2) Si $A\subset F\subset\mathbb{R}^n$ y $F$ es cerrado, entonces $\bar{A}\subset F$

Demostración. Para probar que $\bar{A}\subset F$ mostraremos que el complemento de $F$, $F^c$ está contenido en el complemento de $\bar{A}^c$ de $\bar{A}$. Sea $\bar{x}\in F^c$ como $F$ es cerrado $F^c$ es abierto, luego $\exists$ $r>0$ tal que $B(\bar{x},r)\subset F^c$ pero $A\subset F$

$\therefore$ $F^c\subset A^c$ de donde $B(\bar{x},r)\subset
A^c$ o sea $B(\bar{x},r)\cap A=\emptyset$ esto significa que
$\bar{x}$ no es punto adherente de $A$ es decir $\bar{x}\not\in\bar{A}$ asi que $\bar{x}\in\bar{A}^c$.

Punto de Acumulación

Ejemplo. Sea $A$ un subconjunto arbitrario de $\mathbb{R}^{n}$. Se dice que $\overline{x}\in \mathbb{R^{n}}$ es un punto de acumulación de A, si toda bola abierta con centro en $\overline{x}$ contiene un punto de A distinto de $\overline{x}$ es decir $$\forall r>0 \quad \left(B(\overline{x},r)-{\overline{x}}\right)\bigcap A\neq \emptyset$$
Al conjunto de puntos de acumulación de A se le denomina el conjunto derivado de A y se le denota $A^{a}$

Sea $$A=\{(x,y)\in\mathbb{R}^{2}~|~x^{2}+y^{2}<1\}=B((0,0),1)$$
Probaremos que el punto $$\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$$
que no pertenece a $A$, es punto de acumulación de $A$.

Dado $r>0$ se tiene que
$$\left(\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)},\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)}\right)=\frac{1}{\sqrt{2}(r+1)}(1,1)$$
es tal que
$$\left|\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)},\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)}\right|=\frac{1}{\sqrt{2}(r+1)}|(1,1)|$$
$$=\frac{1}{\sqrt{2}(r+1)}\sqrt{2}$$
$$=\frac{1}{r+1}$$
$$<1$$

y por lo tanto pertenece a $A$. Por otra parte, se tiene que
$$0<\left|\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)-\left(\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)},\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)}\right)\right|$$
$$=\left|\frac{r}{\sqrt{2}(r+1)},\frac{r}{\sqrt{2}(r+1)}\right|$$
$$=\frac{r}{\sqrt{2}(r+1)}|(1,1)|$$
$$=\frac{r}{\sqrt{2}(r+1)}\sqrt{2}$$
$$=\frac{r}{r+1}$$
$$<r$$

de donde concluimos que este punto también pertenece al conjunto

$$B\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},r\right)-\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$$
y por lo tanto que
$$\left(B\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},r\right)-\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\right)\bigcap A \neq \emptyset$$
es decir, que
$$\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$$
es un punto de acumulación de $A$.

Ejemplo. Tenemos
$$A=(a,b)~\Rightarrow~A’=[a,b]$$
$$A=[0,1)-{2}~\Rightarrow~A’=[0,1]$$
$$A=\left\{\frac{1}{k}~\big|~k\in\mathbb{N}\right\}~\Rightarrow~A’=\left\{0\right\}$$

Tarea Moral

Sean $A$ y $B$ subconjuntos de $\mathbb{R}^n$.

Indica y prueba si las siguientes afirmaciónes son ciertas.

1.- Si $A \subset B$ entonces $\overline{A}\subset \overline{B}$

2.- $\overline{A \cup B}$ = $\overline{A} \cup \overline{B}$

3.- $A$ es cerrado si y sólo si $A \cup A ´= \overline{A}$

Sea $A=\{ (m,0) \in \mathbb{R}^2 | m \in \mathbb{Z} \}$

4.- Indica quién es $A’$

5.- Indica quién es $\overline{A}$

Introduccion

La interpretación geométrica de un diferencial en cálculo está relacionada con el cambio local de una función, es deicr, cómo cambia su función cuando varía por poco las entradas de la función. En otras palabras representa una aproximación lineal al cambio de una función.

Diferenciales de funciones $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$

Tenemos que $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ es diferenciable si
$$f(x_{o}+h_{1},y_{0}+h_{2})=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$
cumple
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
Esto se puede escribir como
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$

tomando
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\triangle z$$
$$\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}=\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x$$
$$\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}=\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y$$
tenemos que
$$\triangle z=\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y+r(\triangle x,\triangle y)$$
haciendo $\triangle x,~\triangle y\rightarrow 0$ tenemos
$$dz=\frac{\partial f}{\partial x}(x_{0},y_{0})dx+\frac{\partial f}{\partial y}(x_{0},y_{0}) dy$$
$\textbf{Definición.}$Si $z=f(x,y)$ es una función diferenciable, la diferencial de f denotada $dz$ se define
$$dz=\frac{\partial f}{\partial x}(x_{0},y_{0})dx+\frac{\partial f}{\partial y}(x_{0},y_{0}) dy$$

$\textbf{Ejemplo.}$ Calcular la diferencial de $z=4x^{2}-xy$\En este caso
$$dz=\frac{\partial (4x^{2}-xy)}{\partial x}dx+\frac{\partial (4x^{2}-xy)}{\partial y}dy=(8x-y)dx-xdy$$

Ahora bien
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\triangle z\approx \frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y$$
expresa el cambio aproximado de $z=f(x,y)$ cuando $(x,y)$ pasa a $(x+\triangle x,y+\triangle y)$

Ejemplo. Aproximar el cambio de $z=4x^{2}-xy$ cuando $(x,y)$ pasa de $(2,1)$ a $(2.1,1.5)$\
En este caso tomamos $x_{0}=2$, $y_{0}=1$, $\triangle x=0.1$ y $\triangle y=.5$ y el valor de cambio será
$$\frac{\partial f}{\partial x}(2,1)\triangle x+\frac{\partial f}{\partial y}(2,1)\triangle y=(15)(0.1)-2(0.5)=1.5$$
mientras que
$$f(2.1,1.5)-f(2,1)=14.49-14=0.49$$
por lo tanto en la aproximacion se cometió un error de $0.01$

Ejemplo. Usando diferenciales se quiere calcular aproximadamente
$$A=\frac{0.97}{\sqrt{15.05}+\sqrt[3]{0.98}}$$

Solución. Considerando la función
$$f(x,y,z)=\frac{x}{\sqrt{y+\sqrt[3]{z}}}$$
con $x=1$, $y=15$, $z=1$, $dx=-0.03$, $dy=0.05$ y $dz=-0.02$ se tiene
$$f(x+dx,y+dy,z+dz)=f(x,y,z)+df(x,y,z)$$
en este caso
$$f(x,y,z)=f(1,15,1)=\frac{1}{4}$$
$$\frac{\partial f}{\partial x}=\frac{1}{\sqrt{y}+\sqrt[3]{z}},~\frac{\partial f}{\partial y}=-\frac{x}{2}\left(y+\sqrt[3]{z}\right)^{\frac{-3}{2}},~\frac{\partial f}{\partial z}=-\frac{x}{2}(y+\sqrt[3]{z})^{\frac{-3}{2}}\frac{1}{3}z^{\frac{-2}{3}}$$
evaluando en $(1,15,1)$ se tiene
$$\frac{\partial f}{\partial x}(1,15,1)=\frac{1}{4},~\frac{\partial f}{\partial y}(1,15,1)=-\frac{1}{128},~\frac{\partial f}{\partial z}(1,15,1)=-\frac{1}{384}$$
de modo que
$$df(1,15,1)=\frac{1}{4}(-0.03)-\frac{1}{128}(0.05)-\frac{1}{384}(-0.02)=-\frac{3.01}{384}$$
por lo que
$$A=\frac{1}{4}-\frac{3.01}{384}=0.242161$$
(el valor es $0.2421726$)

Diferencial de orden 2

Si $\displaystyle{df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy}$ entonces una diferencial de orden 2 seria:
$$d^{2}f=d(df)=d\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)dx+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)dy$$
$$=\left(\frac{\partial^{2} f}{\partial x^{2}}dx+\frac{\partial^{2} f}{\partial x\partial y}dy\right)dx+\left(\frac{\partial^{2} f}{\partial y\partial x}dx+\frac{\partial^{2} f}{\partial y^{2}}dy\right)dy=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y\partial x}dydx+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
$$=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
Por lo tanto

$$d^{2}f=d(df)=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$

Ejemplo. Hallar la diferencial de orden 2 para $f(x,y)=e^{x^{2}+y^{y}}$

Solución. En este caso tenemos la fórmula
$$d^{2}f=d(df)=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
vamos a calcular las derivadas parciales correspondientes
$$\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}=2xe^{x^{2}+y^{2}}$$
$$\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}=2ye^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial x^{2}}=\frac{\partial}{\partial x}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}\right)=\frac{\partial(2xe^{x^{2}+y^{2}})}{\partial x}=4x^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial y^{2}}=\frac{\partial}{\partial y}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}\right)=\frac{\partial(2ye^{x^{2}+y^{2}})}{\partial y}=4y^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial y\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}\right)=\frac{\partial (2xe^{x^{2}+y^{2}})}{\partial y}=4xye^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial x\partial y}=\frac{\partial}{\partial x}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}\right)=\frac{\partial (2ye^{x^{2}+y^{2}})}{\partial x}=4xye^{x^{2}+y^{2}}$$
y la diferencial de orden 2 sería:
$$d^{2}f=\left(4x^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}\right)dx^{2}+8xye^{x^{2}+y^{2}}dxdy+\left(4y^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}\right)dy^{2}$$

Diferencial de orden 3

Si $\displaystyle{d^{2}f=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}}$ entonces una diferencial de orden 3 seria:
$$d^{3}f=d(d^{2}f)=d\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)=$$
$$\frac{\partial}{\partial x}\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)dx+\frac{\partial}{\partial y}\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)dy=$$

$$\left(\frac{\partial^{3} f}{\partial x^{3}}dx^{2}+2\frac{\partial^{3} f}{\partial x^{2}\partial y}dxdy+\frac{\partial^{3} f}{\partial x\partial y^{2}}dy^{2}\right)dx+\left(\frac{\partial^{3} f}{\partial x^{2} \partial y}dx^{2}+2\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy+\frac{\partial^{3} f}{\partial y^{3}}dy^{2}\right)dy=$$

$$\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+2\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial x^{2} \partial y}dydx^{2}+2\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}=$$

$$\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}$$
Por lo tanto
$$d^{3}f=d(d^{2}f)=\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}$$

Diferencial de orden 3

Si $\displaystyle{d^{3}f=\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}}$ entonces una diferencial de orden 4 seria:
$$d^{4}f=d(d^{3}f)=\frac{\partial^{4} f}{\partial x^{4}}dx^{4}+4\frac{\partial^{4} f}{\partial x^{3}\partial y}dx^{3}dy+6\frac{\partial^{4} f}{\partial x^{2}\partial y^{2}}dx^{2}dy^{2}+4\frac{\partial^{4} f}{\partial x\partial y^{3}}dxdy^{3}+\frac{\partial^{4} f}{\partial y^{4}}dy^{4}$$

Diferencial de orden n

$$d^{n}f=\frac{\partial^{n} f}{\partial x^{n}}dx^{n}+\left(\begin{matrix}n\\1\end{matrix}\right)\frac{\partial^{n-1} f}{\partial x^{n-1}\partial y}dx^{n-1}dy+\left(\begin{matrix}n\\2\end{matrix}\right)\frac{\partial^{n-2} f}{\partial x^{n-2}\partial y^{2}}dx^{n-2}dy^{2}+\cdots+\left(\begin{matrix}n\\k\end{matrix}\right)\frac{\partial^{n-k} f}{\partial x^{n-k}\partial y^{k}}dx^{n-k}dy^{k}+\cdots+\frac{\partial^{n}f}{\partial y^{n}}dy^{n}$$

que se puede escribir
$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$

Mas adelante

Tarea Moral

1.- Aproximar el cambio de $z=6y^2-5xy+x$ cuando $(x,y)$ pasa de $(0,0)$ a $(0.5, 2.5)$

2.- Aproximar el cambio de $z=4xy$ cuando (x,y) pasa de $(1,2)$ a $(1.3, 4.2)$

3.- Usa diferenciales para calcular aproximadamente
$$A=\frac{1.02}{\sqrt{9.95}+\sqrt[3]{81}}$$

4.- Hallar el diferencial de orden 2 para $f(x,y)= 3x^2+\sqrt{xy}$

5.- Hallar el diferencial de orden 3 para $f(x,y)=sen(4x+y^2)$

Enlaces