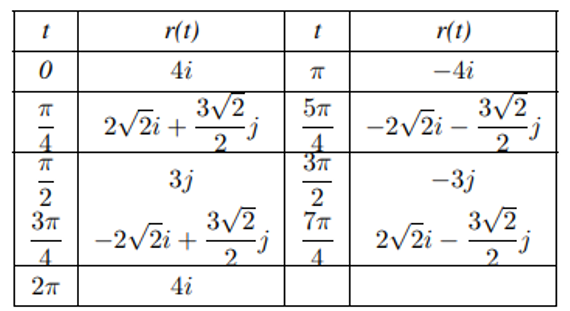Introducción

Una función vectorial es una función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ ó $f:\mathbb{R}\rightarrow\mathbb{R}^{3}$ de la forma
$$f(t)=x(t)i+y(t)j~~\acute{o}~~f(t)=x(t)i+y(t)j+z(t)k$$
donde las funciones componentes $x(t)$, $y(t)$ y $z(t)$ son funciones de valor real del parámetro t. Las funciones con valores vectoriales son también escritas en forma
$$f(t)=(x(t),y(t))~\acute{o}~f(t)=(x(t),y(t),z(t))$$
En ambos casos, la primera forma de la función define una función vectorial bidimensional; la segunda forma describe una función vectorial tridimensional.

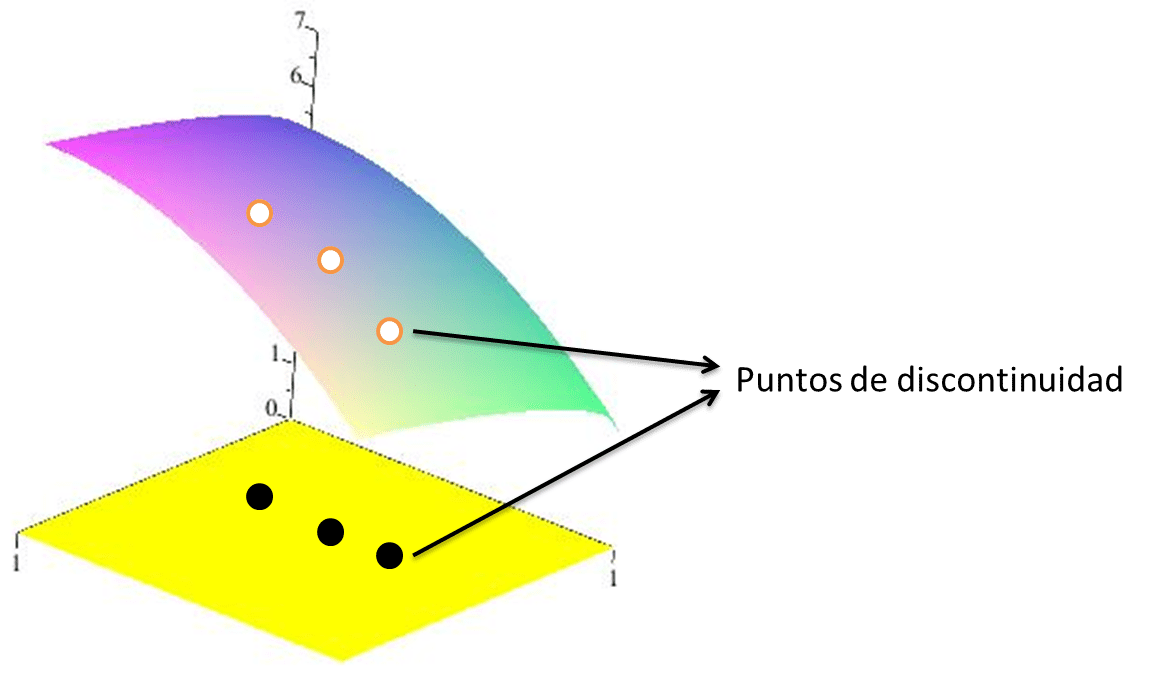
En el siguiente applet desarrollado en Geogebra, podrás manipular un parametro d, dentro de un intervalo $[a,b]$, de tal manera que podrás observar como se va dibujando una curva en el plano.

De acuerdo al applet, el parámetro $d$ puede estar entre dos números reales: $a \leq d \leq b$. Otra posibilidad es que el valor de d tome todos los numeros reales. Las funciones de los componentes en sí mismas pueden tener restricciones de dominio que imponen restricciones en el valor de t. A menudo usamos $t$ como parámetro porque $t$ puede representar el tiempo.

Las rectas en el plano, las podemos pensar como un conjunto definido de la siguiente forma:
$$\ell=\left\{(x,y)\in\mathbb{R}^{2}~\Big{|}~ax+by+c=0\right\}$$
Si $a\neq 0$ entonces para cualquier $(x,y)\in\ell$ se tiene
$$x=\frac{-c-by}{a}$$
Por tanto, a la pareja $(x,y)$ la podemos escribir como
$$\left(\frac{-c-by}{a},y\right)$$
es decir, la podemos escribir en términos de una sola variable. Por lo que si consideramos la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(t)=\left(\frac{-c-bt}{a},t\right)$$
se cumple que $f(\mathbb{R})=\ell$, es decir, que la imagen de la función es toda la recta.

En efecto, para cualquier elemento $t$ en $f(\mathbb{R})$ se cumple
$$a\left(\frac{-c-bt}{a}\right)+bt+c=(-c-bt)+bt+c=0$$
con lo cual concluimos $f(\mathbb{R})\subset \ell$. Por otra parte, si $(x,y)\in\ell$, basta tomar $t=y$ para que se cumpla
$$f(y)=\left(\frac{-c-by}{a},y\right)=(x,y)$$
con lo que concluimos que $\ell\subset f(\mathbb{R})$ y por lo tanto $f((\mathbb{R}))=\ell$.$~~\blacksquare$

Con un razonamiento similar se puede probar que la circunferencia con centro en el origen y radio $r$, se puede describir como el conjunto
$$C_{r}=\left\{(x,y)\in\mathbb{R}^{2}~\Big{|}~x^{2}+y^{2}=r^{2}\right\}$$
y dicho conjunto se puede obtener como la imagen de la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(t)=(r\cos(t),r\sin(t)),~~t\in[0,2\pi].~~\blacksquare$$

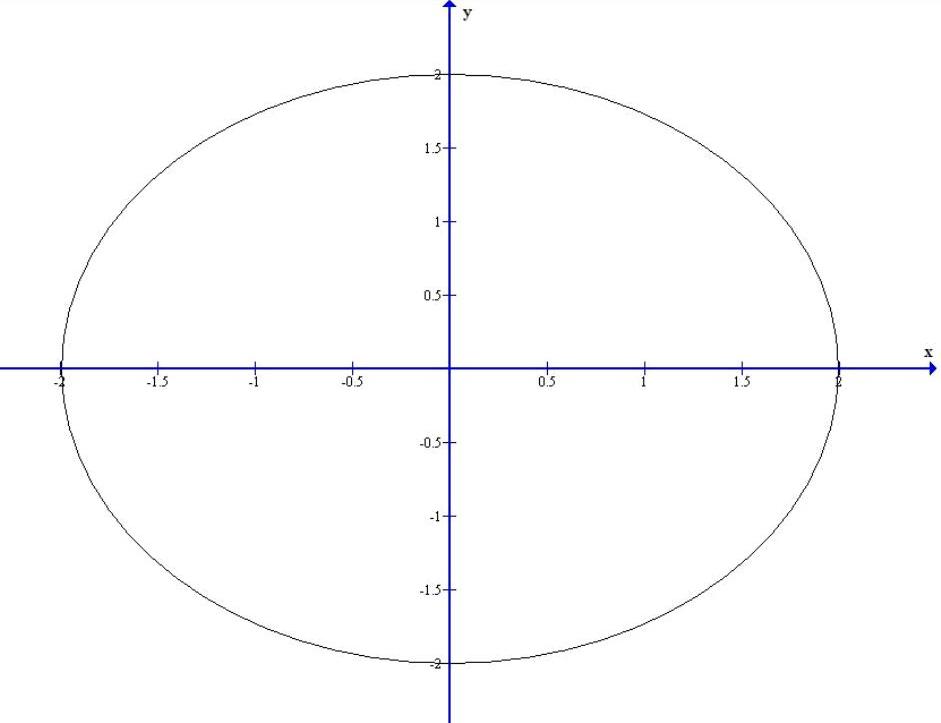
Con un razonamiento similar se puede probar que la elipse, se puede describir como el conjunto
$$E=\left\{(x,y)\in\mathbb{R}^{2}~\Big{|}~\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\right\}$$
y dicho conjunto se puede obtener como la imagen de la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$\boxed{f(t)=(a\cos(t),b\sin(t)),~~t\in[0,2\pi].}$$ $\blacksquare$

En general si un subconjunto $C\subset \mathbb{R}^{n}$ es tal que coincide con la imagen de una función $f:\mathbb{R}\rightarrow\mathbb{R}^{n}$, diremos que dicha función es una parametrización de C.

Definición. Sea $C\subset\mathbb{R}^{n}$. Si existe $\gamma=(\gamma_{1},\gamma_{2},…,\gamma_{n}):\mathbb{R}\rightarrow\mathbb{R}^{n}$ tal que $\gamma(I)=C$ decimos que $\gamma$ es una parametrización de C. En tal caso diremos que las ecuaciones
\begin{align*} x_{1} & =\gamma_{1}(t) \\ x_{2} & =\gamma_{2}(t) \\ \vdots & =\vdots \\ x_{n} & =\gamma_{n}(t) \end{align*}

son unas ecuaciones paramétricas de C.

Ejemplo. Si $f$ es la función vectorial por $f(t)=(2\cos(t),2\sin(t))$ con $t\in[0,2\pi]$, tenemos entonces que $f$ asocia a cada número real $t$ en el intervalo $[0,2\pi]$, un par ordenado $(x,y)$ con $x=2\cos t$ y $y=2\sin t$, que son las ecuaciones paramétricas de una circunferencia de radio 2 y centro en el origen. Asi pues la gráfica de $f$ es una circunferencia.

Cada una de las funciones vectoriales que se dan a continuación,
define el mismo lugar geométrico o una parte de éste; sin embargo,
el sentido, el punto de partida y la rapidez de recorrido así como
la porción de la curva que se considera en cada caso varia.
\begin{align*} f_{1}(t) &=(2\cos t, 2\sin t) \quad t\in[0,2\pi] \\ f_{2}(t) &=(2\cos t, 2\sin t) \quad t\in[0,\pi] \\ f_{3}(t) &=(2\cos 3t, 2\sin 3t) \quad t\in[0,2\pi] \\ f_{4}(t) &=(2\cos t, 2\sin t) \quad t\in[0,\pi] \\f_{5}(t) &=(2\cos t, 2\sin t) \quad t\in[0,6\pi] \\ f_{6}(t) &=(2\cos t, 2\sin t) \quad t\in[-\pi,\pi] \end{align*}

Para una función vectorial en $\mathbb{R}^{3}$ decimos que: Si $D$ es un conjunto de $\mathbb{R}$, entonces $f(t)$ es una función vectorial con dominio $D$ si y sólo si, para todo $t\,\epsilon\,D$
$$f(t)=x_{1}(t)i+x_{2}(t)j+x_{3}(t)k$$
donde $x_{1}(t),x_{2}(t)$ y $x_{3}(t)$ son funciones escalares con dominio $D$. $\blacksquare$

Ejemplo. Que representa la función vectorial cuyas ecuaciones parametricas son:
$$f(t)=\left(\frac{1-t^{2}}{1+t^{2}},\frac{2t}{1+t^{2}}\right)$$

En este caso haciendo la sustitución $\displaystyle{t=\tan\left(\frac{u}{2}\right)}$ se tiene que

$$\frac{1-t^{2}}{1+t^{2}}=\frac{1-\tan^{2}\left(\frac{u}{2}\right)}{1+\tan^{2}\left(\frac{u}{2}\right)}=\frac{1-\frac{\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}{1+\frac{\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}=\frac{\frac{\cos^{2}\left(\frac{u}{2}\right)-\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}{\frac{\cos^{2}\left(\frac{u}{2}\right)+\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}=\frac{\cos^{2}\left(\frac{u}{2}\right)-\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)+\sin^{2}\left(\frac{u}{2}\right)}=\cos^{2}\left(\frac{u}{2}\right)-\sin^{2}\left(\frac{u}{2}\right)$$
$$=\cos\left(\frac{2u}{2}\right)=\cos(u)$$
$$\frac{2t}{1+t^{2}}=\frac{2\tan\left(\frac{u}{2}\right)}{1+\tan^{2}\left(\frac{u}{2}\right)}=2\frac{\frac{\sin\left(\frac{u}{2}\right)}{\cos\left(\frac{u}{2}\right)}}{1+\frac{\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}=2\frac{\frac{\sin\left(\frac{u}{2}\right)}{\cos\left(\frac{u}{2}\right)}}{\frac{\cos^{2}\left(\frac{u}{2}\right)+\sin^{2}\left(\frac{u}{2}\right)}{\cos^{2}\left(\frac{u}{2}\right)}}=2\sin\left(\frac{u}{2}\right)\cos\left(\frac{u}{2}\right)=\sin\left(\frac{2u}{2}\right)=\sin(u)$$
donde $u\in[0,\pi]$. Al ser
$$\left(\frac{1-t^{2}}{1+t^{2}}\right)^{2}+\left(\frac{2t}{1+t^{2}}\right)^{2}=\cos^{2}(u)+\sin^{2}(u)=1$$ se trata de una circunferencia de radio 1 con centro en el origen. $\blacksquare$

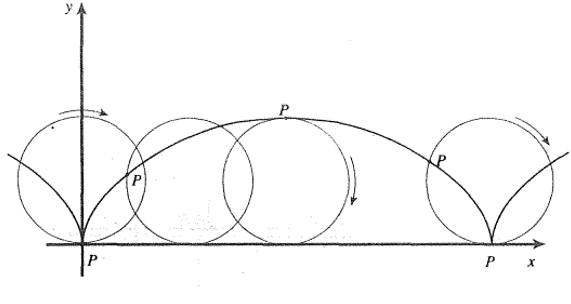
Ejemplo.Parametrización de la curva Cicloide.

Supongamos que un círculo de radio a rueda sin deslizarse a lo largo de una línea recta horizontal. Encuentre la curva descrita por un punto fijo P de su circunferencia.

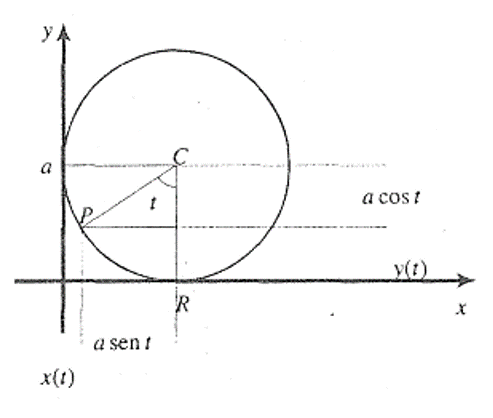
Sea t el ángulo en radianes, que forma (la línea que contiene) el radio CP con la línea CR.

Nótese que $OR$ es justamente la longitud de arco RP que es igual a $at$, de modo que el punto C tiene coordenadas $C=(at,a)$. Si $(x(t),y(t))$ denotan las coordenadas del punto p, se tiene

$$x(t)=at+a\sin(t)$$

$$y(t)=a+a\cos(t)$$

Por lo que la cicloide se puede representar por la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(t)=(at+a\sin(t),a+a\cos(t))$$
Si se despeja la variable t en la ecuación paramétrica, se obtendrá la forma cartesiana:
$$x=a\arcsin\left(\frac{y}{a}-1\right)+\left(y-a\right)$$. $\blacksquare$
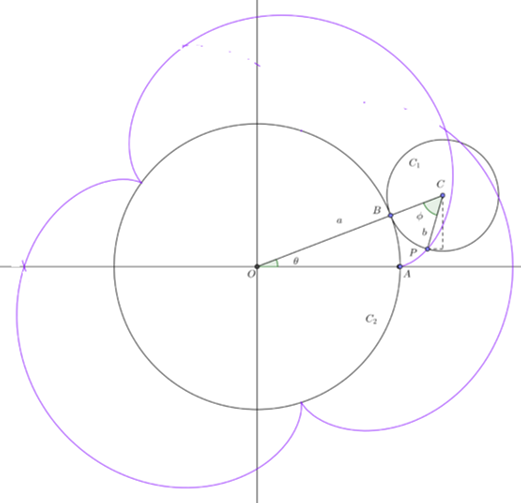
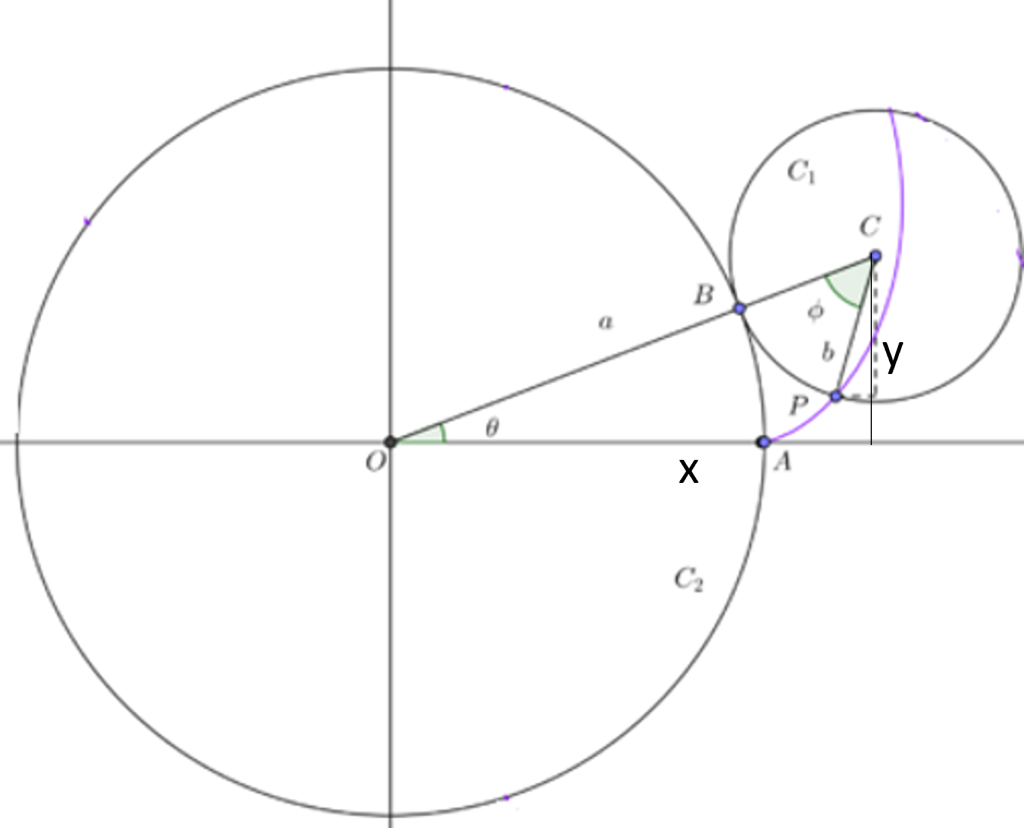
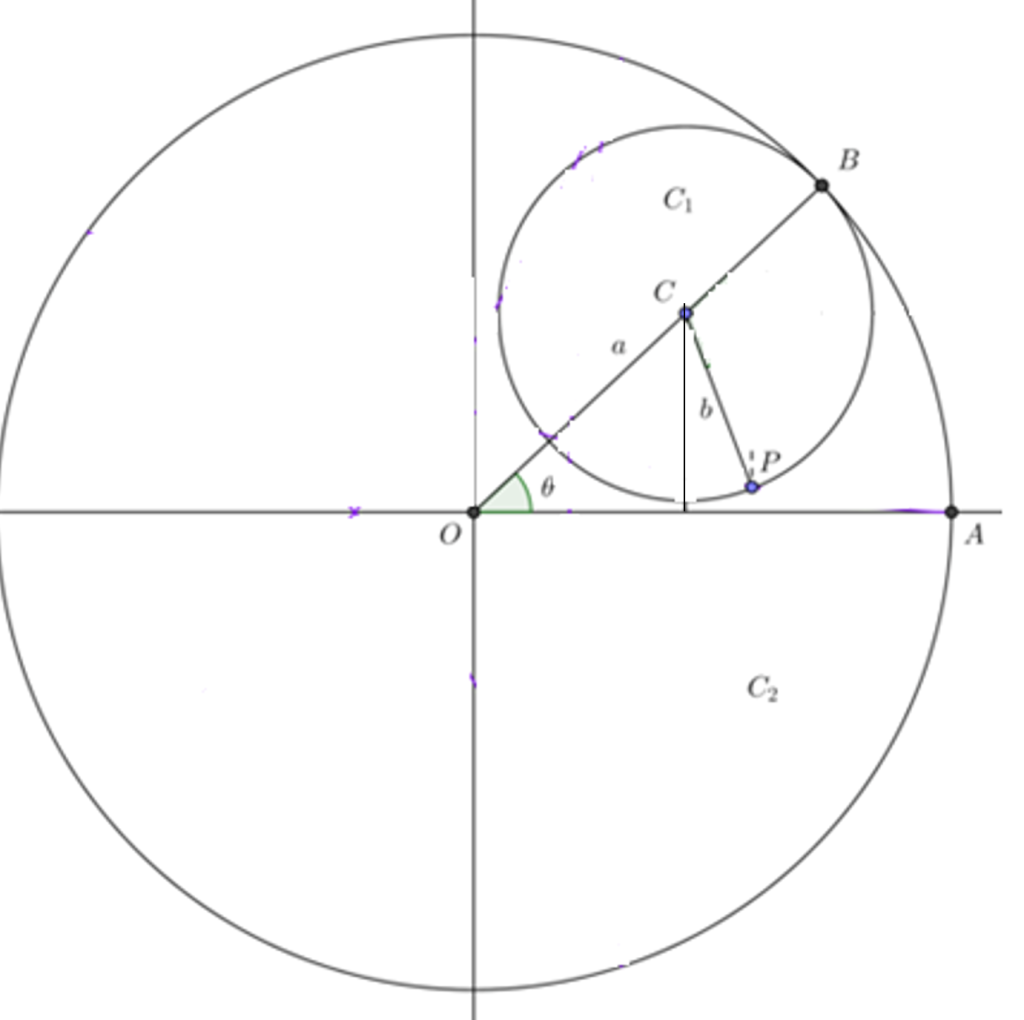
Ejemplo. Parametrización de la curva Epicicloide.
Supongamos que un círculo de radio a rueda sin deslizarse sobre una circunferencia. Encuentre la curva descrita por un punto fijo $P$ de su circunferencia.

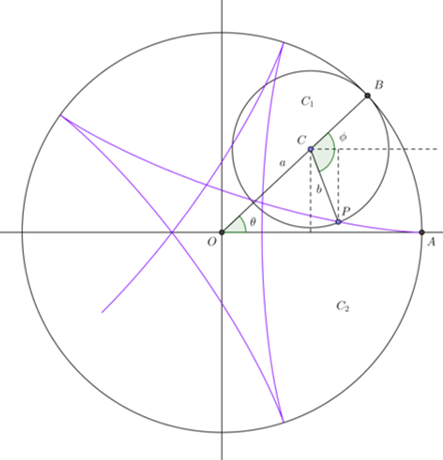
De acuerdo a la siguiente figura

\begin{align*}\cos(\theta) & =\frac{x_{c1}}{a+b}&\Rightarrow~x_{c1}=(a+b)\cos(\theta) \\sin(\theta) & =\frac{y_{c1}}{a+b}&\Rightarrow~y_{c1}=(a+b)\sin(\theta)\end{align*}
También se tiene que el arco de circulo $C_{1}PB$ es igual al arco de circulo $C_{2}AB$ esto es
$$a\theta=b\phi~\Rightarrow~\frac{a}{b}\theta=\phi$$
Ahora de acuerdo a la figura

$$\theta+\phi-\beta=\pi~\Rightarrow~\beta=\pi-\theta+\phi$$
Por lo que usando que $\cos$ es par
\begin{align*} P\in C_{1} &~\Leftrightarrow~P\in (b\cos(\beta),b\sin(\beta)) \\ &~\Leftrightarrow~P\in (b\cos(\theta+\phi-\pi),b\sin(\theta+\phi-\pi)) \\ &~\Leftrightarrow~P\in (-b\cos(\theta+\phi),-b\sin(\theta+\phi)) \end{align*}
Utilizando todo lo anterior
\begin{align*} x & =\left((a+b)\cos(\theta)-b\cos(\theta+\phi)\right) \\ y & =\left((a+b)\sin(\theta)-b\sin(\theta+\phi)\right) \end{align*}
Como $\displaystyle{\frac{a}{b}\theta=\phi}$ tenemos
\begin{align*} x & =\left((a+b)\cos(\theta)-b\cos\left(\theta+\frac{a}{b}\theta\right)\right) \\ y & =\left((a+b)\sin(\theta)-b\sin\left(\theta+\frac{a}{b}\theta\right)\right) \end{align*}
Por lo que la Epicicloide se puede representar por la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(\theta)=\left((a+b)\cos(\theta)-b\cos\left(\theta+\frac{a}{b}\theta\right),(a+b)\sin(\theta)-b\sin\left(\theta+\frac{a}{b}\theta\right)\right)$$ $\blacksquare$
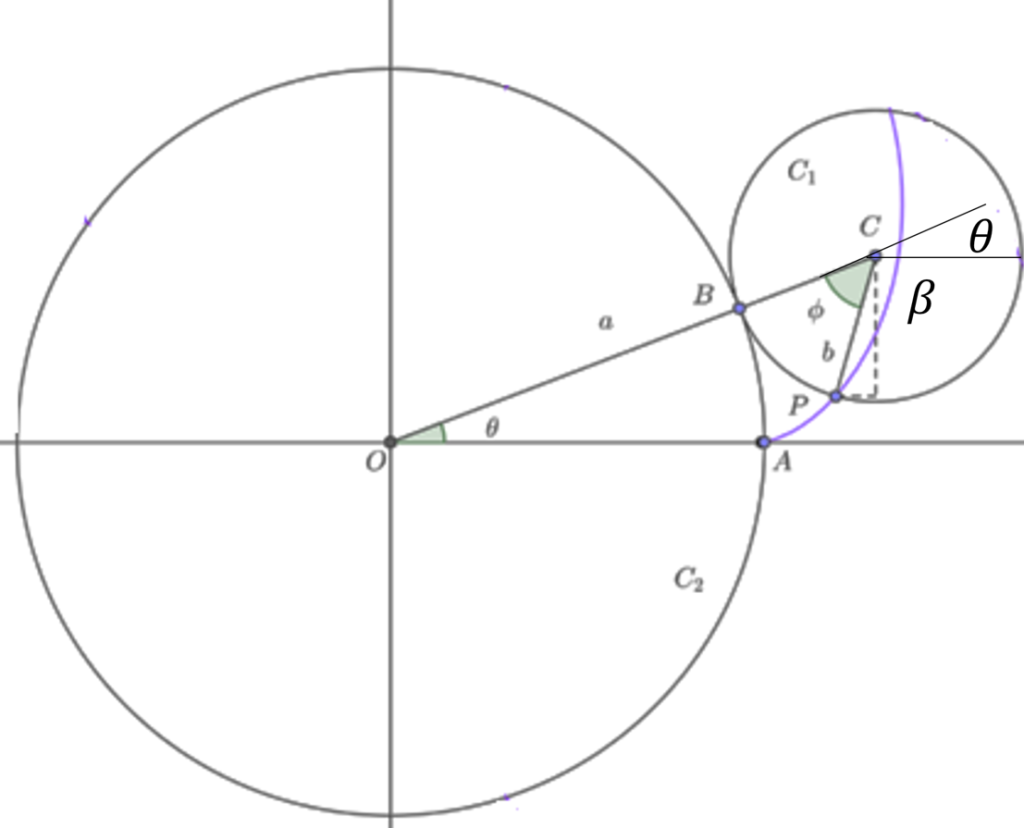
Ejemplo. Parametrización de la curva Hipocicloide.
Una curva hipocicloide es la trayectoria descrita por un punto P situado sobre una circunferencia que rueda sin deslizar por el interior de otra circunferencia.

De acuerdo a la siguiente figura se tiene

\begin{align*} \cos(\theta) & =\frac{x}{a-b}&\Rightarrow~x=(a-b)\cos(\theta) \\sin(\theta) & =\frac{y}{a-b}&\Rightarrow~y=(a-b)\sin(\theta) \end{align*}
También se tiene que el arco de circulo $C_{1}PB$ es igual al arco de circulo $C_{2}AB$ esto es
$$a\theta=b\phi~\Rightarrow~\frac{a}{b}\theta=\phi$$
Ahora de acuerdo a la figura

$$\phi-\theta=\frac{a}{b}\theta-\theta$$
Utilizando todo lo anterior
\begin{align*} x & =\left((a-b)\cos(\theta)+b\cos(\phi-\theta)\right) \ y & =\left((a+b)\sin(\theta)-b\sin(\phi-\theta)\right) \end{align*}
Como $\displaystyle{\frac{a}{b}\theta=\phi}$ tenemos
\begin{align*} x & =\left((a-b)\cos(\theta)+b\cos\left(\frac{a}{b}\theta-\theta\right)\right) \ y & =\left((a+b)\sin(\theta)-b\sin\left(\frac{a}{b}\theta-\theta\right)\right) \end{align*}
Por lo que la Epicicloide se puede representar por la función $f:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por
$$f(\theta)=\left((a-b)\cos(\theta)+b\cos\left(\frac{a}{b}\theta-\theta\right),(a-b)\sin(\theta)-b\sin\left(\frac{a}{b}\theta-\theta\right)\right)$$. $\blacksquare$

Funciones vectoriales $f:\mathbb{R}\rightarrow\mathbb{R}^{3}$

Supongamos el espacio tridimensional $\mathbb{R}^{3}$ dotado del sistema de coordenadas $(x,y,z)$. Una curva C parametrizada en este espacio es la representación gráfica de una función vectorial:
$$r(t)=(x(t),y(t),z(t))$$
donde t se denomina el parámetro de una curva, $t\in\mathbb{R}$. La estructura de la
curva dependerá de las funciones $x(t), y(t)~ y~z(t)$.
Ejemplo. Describa la curva definida por la función vectorial $r(t)=(1+t,2+5t,-1+6t)$.

En este caso las ecuaciones paramétricas correspondiente son, $x=1+t$,
$y=2+5t$, $z=1+6t$ o sea $r(t)=(1,2,-1)+t(1,5,6)$
se trata de una recta que pasa por $(1,2,-1)$ y es paralela a $(1,5,6)$.$\blacksquare$

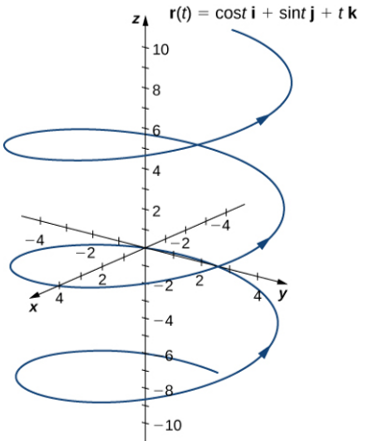
Ejemplo. Dibuje la curva cuya ecuación vectorial es $r(t)=2\cos ti+\sin tj+tk$.
En este caso, las ecuaciones paramétricas para esta curva son, $x=2\cos t$, $y=\sin t$, $z=t$, por lo que $\displaystyle{x/2=\cos t}$
$\therefore$ $\qquad$ $\displaystyle{\left(\frac{x}{2}\right)^{2}+y^{2}=1}$ la curva se encuentra en el cilindro elíptico $\displaystyle{\left(\frac{x^{2}}{4}\right)^{2}+y^{2}=1}$. Ya que $z=t$ la curva forma una espiral ascendente alrededor del cilindro conforme $t$ se incrementa

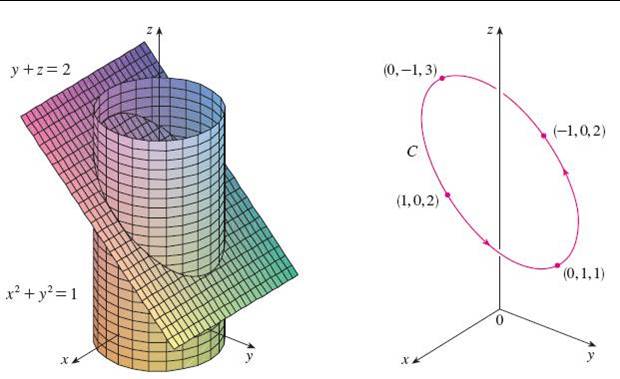
Ejemplo. Halle una función vectorial que represente la curva de la intersección del cilindro $x^{2}+y^{2}=1$ y el plano $y+z=2$.
En este caso la figura muestra la forma en que se cruzan, el plano y el cilindro, así mismo la figura ilustra la curva de intersección.

La proyección $C$ sobre el plano $xy$ es el circulo $x^{2}+y^{2}=1$, $z=0$, que podemos parametrizar como $x=\cos t$, $y=\sin t$, $0\leq t \leq 2\pi$, con base en la ecuacion del plano, tenemos que $$z=2-y=2-\sin t$$
$\therefore~~~x=\cos t,~~y=\sin t,~~z=2-\sin t,~~~0\leq t \leq 2\pi$
$\therefore$ la ecuación vectorial correspondiente es
$$r(t)=\cos ti+\sin tj+(2-\sin t)k \qquad 0\leq t \leq 2\pi$$ $\blacksquare$

Dominio de la Función Vectorial

El dominio de una función vectorial $r(t)$ es el conjunto de valores permitidos de $t$. Si $r(t)$ se define en términos de las funciones de las componentes y no se especifica explícitamente el dominio, entonces se sobreentiende que el dominio es la intersección de los dominios naturales de las funciones de las componentes, por lo que éste recibe el nombre de dominio natural de $r(t)$.
Sea $f(t)=(x_{1}(t)),x_{2}(t)),…,x_{n}(t))~\in\mathbb{R}^{n}$ entonces el $\displaystyle{Dom_{f}=\bigcap_{i=1}^{n} Dom_{x_{i}}}$

Ejemplo. Halle el dominio de la función vectorial
$$f(t)=\left(t^{2},\sqrt{t-1},\sqrt{5-t}\right)$$

tenemos que
\[Si\quad x_{1}(t)=t^{2}\quad entonces\quad \textit{Dom} (x_{1}(t))=\{\mathbb{R}\}\]
\[Si\quad x_{2}(t)=\sqrt{t-1}\quad entonces\quad \textit{Dom} (x_{2}(t))=\{t\in\mathbb{R}~|~t\geq1\}\]
\[Si\quad x_{3}(t)=\sqrt{5-t}\quad entonces\quad \textit{Dom} (x_{3}(t))=\{t\in\mathbb{R}~|~5\geq t\}\]
Por lo tanto
\[\textit{Dom} (f(t))=\bigcap{\textit{Dom} (x_{1}(t)),\textit{Dom} (x_{2}(t)),\textit{Dom} (x_{3}(t))}=\{t\in\mathbb{R}~|~1~\leq t~\leq 5\} \]. $\blacksquare$

Halle el dominio de la función vectorial
$$f(t)=\left(Ln(t),\frac{t}{t-1},e^{-t}\right)$$

tenemos que
\[Si\quad x_{1}(t)=Ln(t)\quad entonces\quad \textit{Dom} (x_{1}(t))=\{t\in\mathbb{R}|0<t\}\]
\[Si\quad x_{2}(t)=\frac{t}{t-1}\quad entonces\quad \textit{Dom} (x_{2}(t))=\{t\in\mathbb{R}|1\neq t\}\]
\[Si\quad x_{3}(t)=e^{-t}\quad entonces\quad \textit{Dom} (x_{3}(t))=\{\mathbb{R}\}\]
Por lo tanto
\[\textit{Dom} (f(t))=\bigcap{\textit{Dom} (x_{1}(t)),\textit{Dom} (x_{2}(t)),\textit{Dom} (x_{3}(t))}=\{t\in\mathbb{R}~|~0< t,\quad t\neq1\} \].$$\blacksquare$$

Graficar funciones con valores vectoriales

Recuerda que un vector plano consta de dos cantidades: dirección y magnitud. Dado cualquier punto en el plano (el punto inicial), si nos movemos en una dirección específica por una distancia específica, llegamos a un segundo punto. Esto representa el punto final de el vector. Calculamos las componentes del vector restando las coordenadas del punto inicial a las coordenadas del punto terminal.
Se considera que un vector está en posición estándar si el punto inicial se encuentra en el origen. Al graficar un valor vectorial, por lo general, representamos gráficamente los vectores en el dominio de la función en la posición estándar, porque hacerlo garantiza la unicidad de la gráfica. Esta convención se aplica también a las gráficas de funciones vectoriales tridimensionales.
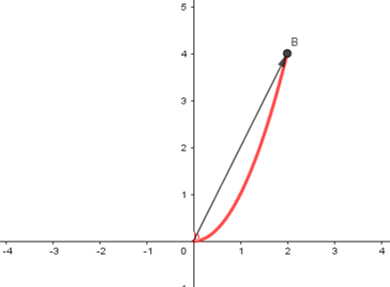
La gráfica de una función vectorial de la forma $r(t)=f(t)i+g(t)j$ consiste en el conjunto de todos $(t,r(t))$, y la ruta que traza se llama curva plana.

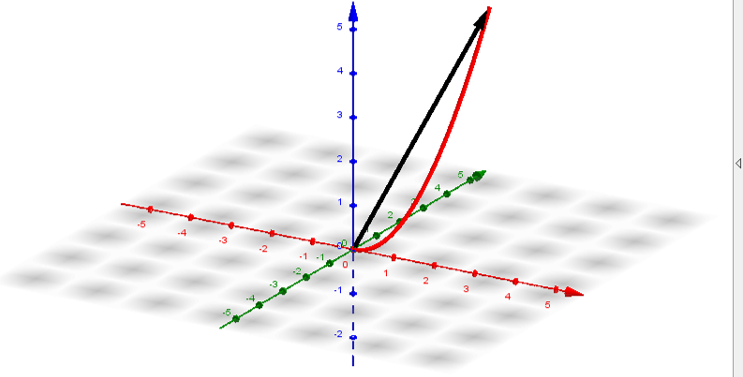
La gráfica de una función vectorial de la forma $r(t) = f(t)i + g(t)j + h(t)k$ consiste en el conjunto de todos $(t, r(t))$, y el camino que traza se llama curva espacial.

Cualquier representación de una curva plana o una curva espacial utilizando un valor vectorial se denomina parametrización vectorial de la curva.

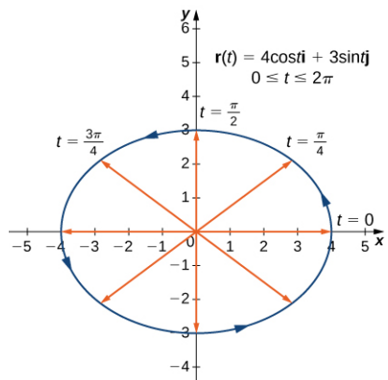
Ejemplo. Cree una gráfica de la siguiente funcion con valores vectoriales:
$$r(t)=4\cos(t)i+3\sin(t)j,~~~0\leq t\leq 2\pi$$

Como con cualquier gráfico, comenzamos con una tabla de valores. Luego graficamos cada uno de los vectores en la segunda columna en posición estándar y conectamos los puntos terminales de cada vector para formar una curva. Esta curva resulta ser una elipse centrada en el origen.

Ejemplo. Cree una gráfica de la siguiente funcion con valores vectoriales:
$$r(t)=\cos(t)i+\sin(t)j+tk,~~~0\leq t\leq 4\pi$$

Realizamos el mismo procedimiento para una función vectorial tridimensional.

Los valores luego se repiten, excepto por el hecho de que el coeficiente de k siempre es creciente. Esta curva se llama hélice. Observe que si se elimina la componente k, entonces la función se convierte en $r(t)=\cos(t)i+\sin(t)j$, que es un círculo unitario centrado en el origen.

Operaciones con Funciones Vectoriales

Las operaciones usuales del algebra vectorial pueden aplicarse para
combinar 2 funciones o una función vectorial con una función real.

Si $f$ y $g$ son funciones vectoriales y si $u$ es una función real, teniendo todas un dominio común, definimos nuevas funciones $F+G$, $uF$ y $F\cdot G$ mediante
\begin{align*}
(F+G)(t)&=F(t)+G(t)\\
u~F(t)&=u(t)~F(t)\\
(F\cdot G) (t)&= F(t)\cdot G(t)\\
(F\times G )(t)&=F(t)\times G(t)~si~F,G\in \mathbb{R}^{3}
\end{align*}

Más adelante

Una vez definido el concepto de función vectorial vamos a aprender a calcular el límite de estas funciones. Cuando calculamos el límite de una sola variable basta que coincidan los límites laterales para saber que existe, pero cuando lo hacemos en más dimensiones tenemos más direcciones de aproximación.

Tarea moral

1.- Sobre la parte exterior de una circunferencia fija de radio a rueda (sin resbalar) otra circunferencia de radio b. Encuentre una función de $\mathbb{R}$ en $\mathbb{R}^{2}$ que describa el movimiento de un punto que se encuentre en la cicunferencia exterior.

2.- Sea $R \subset \mathbb{R}^{2}$ la recta cuya ecuación cartesiana es $ax+by+c=0$ (con $a^2+b^2>0$). Muestra que si $\overline{x_0}=(x_0,y_0)$ y $\overline{x_1}=(x_1,y_1)$ son dos puntos diferentes que pertenecen a $\mathbb{R}$ entonces la función $f(t): \mathbb{R} \rightarrow \mathbb{R^2}$ dada por $f(t)= \overline{x_0} +t( \overline{x_1}- \overline{x_0})$ es una parametrización de $R$

3.- Halla el dominio de la siguiente función vectorial $f:\mathbb{R}\rightarrow \mathbb{R^3}$ donde $f(t)=(t^2, ln(t-2), \sqrt{4-t})$

4.- Dadas las funciones vectoriales $f(t)=(1+t,t^2)$, $g(t)=(t, t^3)$ halla $(fg)(t)$

5.- Crea la gráfica de la siguiente función vectorial $r(t)=(t^2-1)i+(2t-3)j$, $0 \leq t \leq 3$

Enlaces

En el siguiente enlace podrás conocer algunas curvas paramétricas famosas

Dada una función de dos variables que está
definida sobre el rectángulo cerrado
$$R=[a,b]\times[c,d]={(x,y)\in\mathbb{R}^{2}\mid a\leq x\leq b,
c\leq y \leq d}$$ suponiendo que $f(x,y)\geq 0$. La gráfica de f es
una superfície con ecuación $z=f(x,y)$. Sea S el sólido que esta
encima de R y debajo de la gráfica de f, es decir
$$S={(x,y,z)\in \mathbb{R}^{3}\mid 0\leq z\leq f(x,y),(x,y)\in R}$$

Si cortamos nuestra región por un plano paralelo al plano YZ

a la altura del punto $x_{0}\in [a, b]$ del eje X, la figura que se obtiene es la misma que obtenemos al considerar aquella que está por debajo de la gráfica de la función $f_{x_{0}}: [c, d] \rightarrow\mathbb{R}$ definida como
$$f_{x_{0}}(y)=f(x_{0},y)$$
de esta forma, el área de la figura correspondiente al corte realizado a la altura $x_{0}$ que podemos denotar $\alpha(x_{0})$ coincide con ser
$$\alpha(x_{0})=\int_{c}^{d}f(x_{0})(y)dy=\int_{c}^{d}f(x_{0},y)dy$$
También podemos hacer cortes con planos paralelos al plano XZ; así si cortamos a la altura del punto $y_{0}\in [c, d]$ del eje Y

se obtiene es la misma que obtenemos al considerar aquella que está por debajo de la gráfica de la función $f_{y_{0}}: [a, b] \rightarrow\mathbb{R}$ definida como
$$f_{y_{0}}(x)=f(x,y_{0})$$
de esta forma, el área de la figura correspondiente al corte realizado a la altura $y_{0}$ que podemos denotar $\beta(y_{0})$ coincide con ser
$$\beta(y_{0})=\int_{a}^{b}f_{y_{0}}(x)dx=\int_{a}^{b}f(x,y_{0})dx$$
En este caso $\beta$ es una función definida sobre el intervalo $[c, d]$.
Por tanto el volumen del sólido entre la superfície y el rectángulo R estará dado por
$$\int_{R}\alpha(x)dx=\int_{a}^{b}\left(\int_{c}^{d}f(x,y)dy\right)dx$$
o por
$$\int_{R}\beta(x)dy=\int_{c}^{d}\left(\int_{a}^{b}f(x,y)dx\right)dy$$
$\boxed{\Large{\textcolor{red}{Teorema~de~Fubini}}}$
El teorema de Fubini nos va a dar una técnica para el cálculo de integrales de funciones de varias variables mediante el cálculo de varias integrales de funciones de una variable. A partir de ahí se podrán utilizar todas las técnicas conocidas del Análisis de una variable para el cálculo de integrales mediante cálculo de primitivas y el teorema fundamental del cálculo (Regla de Barrow): cambios de variables, integración por partes, etc.
$\boxed{\textcolor{red}{Teorema:}}$
Sean $[a,b]\subset\mathbb{R}$ y $[c,d]\subset \mathbb{R}$ dos intervalos tal que, $R= [a,b]\times [c,d]$, y $f: R\subset\mathbb{R}\rightarrow\mathbb{R}^{2}$ una función integrable.

Para cada $\hat{y}$ fijo en $[c,d]$ definimos $f_{\hat{y}}:[t_{i-1},t_{i}]\subset\mathbb{R}\rightarrow\mathbb{R}$ como
$$f_{\hat{y}}=f(x,\hat{y})$$
y definimos
$$\phi(\hat{y})=\underline{\int_{t_{i-1}}^{t_{i}}}f_{\hat{y}}(x)dx$$
$$\psi(\hat{y})=\overline{\int_{t_{i-1}}^{t_{i}}}f_{\hat{y}}(x)dx$$
Si f es integrable sobre R entonces $\phi, \psi$ son integrables sobre $[c,d]$ y además
$$\int_{R}f=\int_{c}^{d}\phi(y)dy=\int_{c}^{d}\psi(y)dy$$
$\boxed{\textcolor{red}{Demostración:}}$
Observemos en primer lugar que una partición de $R = [a,b]\times [c,d]$ esta formada por una partición de $[a,b]$ y otra de $[c,d]$. Sea $$P_{1}\in P_{[a,b]}=\{a=t_{0},t_{1},…,t_{n}=b\}$$ y sea
$$P_{2}\in P_{[c,d]}=\{c=t_{0},t_{1},…,t_{m}=d\}$$
$$P=P_{1}\times P_{2}\in P_{R} $$
Y cualquier rectángulo de la partición P tiene área $|t_{i}-t_{i-1}|\cdot|t_{j}-t_{j-1}|$,

Para cada $\hat{y}$ fijo en $[c,d]$ definimos
\begin{align*}
m_{j}(\phi)&=\inf\{\phi(\hat{y})~\Big{|}~\hat{y}\in[t_{j-1},t_{j}]\}\\
M_{j}(\phi)&=\sup\{\phi(\hat{y})~\Big{|}~\hat{y}\in[t_{j-1},t_{j}]\}\\
m_{j}(\psi)&=\inf\{\psi(\hat{y})~\Big{|}~\hat{y}\in[t_{j-1},t_{j}]\}\\
M_{j}(\psi)&=\sup\{\psi(\hat{y})~\Big{|}~\hat{y}\in[t_{j-1},t_{j}]\}\\
m_{i}(f_{\hat{y}})&=\inf\{f_{\hat{y}}(x)~\Big{|}~x\in[t_{i-1},t_{i}]\}\\
M_{i}(f_{\hat{y}})&=\sup\{f_{\hat{y}}(x)~\Big{|}~x\in[t_{i-1},t_{i}]\}\\
m_{ij}(f)&=\inf\{f(x,y)~\Big{|}~(x,y)\in R_{ij}\}\\
M_{ij}(f)&=\sup\{f(x,y)~\Big{|}~(x,y)\in R_{ij}\}
\end{align*}
De lo anterior tenemos que se cumple
$$m_{ij}(f)\leq m_{i}(f_{\hat{y}})\leq M_{i}(f_{\hat{y}})\leq M_{ij}(f)$$
Multiplicando por $(t_{i} − t_{i−1}) > 0$ se tiene
$$m_{ij}(f)(t_{i} − t_{i−1}) \leq m_{i}(f_{\hat{y}})(t_{i} − t_{i−1}) \leq M_{i}(f_{\hat{y}})(t_{i} − t_{i−1}) \leq M_{ij}(f)(t_{i} − t_{i−1}) $$
Sumando sobre i
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1}) \leq \sum_{i=1}^{n}m_{i}(f_{\hat{y}})(t_{i} − t_{i−1}) \leq \sum_{i=1}^{n}M_{i}(f_{\hat{y}})(t_{i} − t_{i−1}) \leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1}) $$
se tiene entonces
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1}) \leq \underline{S}(f_{\hat{y}},P) \leq \overline{S}(f_{\hat{y}},P)\leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1}) $$
Sabemos que
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1}) \leq \underline{S}(f_{\hat{y}},P)\leq \phi(\hat{y})\leq \psi(\hat{y})\leq \overline{S}(f_{\hat{y}},P)\leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1}) $$
Esto pasa para toda $\hat{y}\in[c,d]$ esto prueba que los extremos de estas desigualdades son cota inferior y superior (respectivamente) tanto de $\psi$ como de $\phi$ en el subrectángulo $R_{ij}$ y por lo tanto tendremos que
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})\leq m_{j}(\phi)\leq M_{j}(\phi)\leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})$$
y también
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})\leq m_{j}(\psi)\leq M_{j}(\psi)\leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})$$
Multiplicando por $(t_{j} − t_{j−1}) > 0$ se tiene
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) \leq m_{j}(\phi)(t_{j} − t_{j−1}) \leq M_{j}(\phi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) $$
y también
$$\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) \leq m_{j}(\psi)(t_{j} − t_{j−1}) \leq M_{j}(\psi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) $$
Sumando sobre j
$$\sum_{i=1}^{m}\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}m_{j}(\phi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}M_{j}(\phi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}\sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) $$
y también
$$\sum_{i=1}^{m}\sum_{i=1}^{n}m_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}m_{j}(\psi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}M_{j}(\psi)(t_{j} − t_{j−1}) \leq \sum_{i=1}^{m}\sum_{i=1}^{n}M_{ij}(f)(t_{i} − t_{i−1})(t_{j} − t_{j−1}) $$
se tiene entonces
$$\underline{S}(f,P)\leq \underline{S}(\phi,P)\leq \overline{S}(\phi,P)\leq \overline{S}(f,P)$$
y también
$$\underline{S}(f,P)\leq \underline{S}(\psi,P)\leq \overline{S}(\psi,P)\leq \overline{S}(f,P)$$
como f es integrable sobre R, entonces las funciones $\psi$ y $\phi$ son integrables sobre $[c, d]$ y además
$$\int_{R}f=\int_{c}^{d}\phi(y)dy=\int_{c}^{d}\psi(y)dy$$
Es decir
$$\int_{R}=\int_{c}^{d}\left(\int_{a}^{b}f(x,y)dx\right)dy$$
siguiendo estos pasos pero considerando ahora un $x_{o}$ fijo en [a, b] y haciendo variar la y se tendría
$$\int_{R}=\int_{a}^{b}\left(\int_{c}^{d}f(x,y)dy\right)dx$$
Es decir
$$\int_{R}=\int_{a}^{b}\left(\int_{c}^{d}f(x,y)dy\right)dx=\int_{c}^{d}\left(\int_{a}^{b}f(x,y)dx\right)dy\blacksquare$$
$\boxed{\textcolor{green}{Ejemplo}}$
Si $R=[-1,1]\times \left[0,\frac{\pi}{2}\right]$, calcular
$$\int_{R}(x\sin(y)-ye^{x})dxdy$$
$\boxed{\textcolor{green}{Solución}}$
Integrando primero respecto a x tenemos
$$\int_{0}^{\frac{\pi}{2}}\left(\int_{-1}^{1}(x\sin(y)-ye^{x})dx\right)dy=\int_{0}^{\frac{\pi}{2}}\left(\frac{x^{2}}{2}\sin(y)-ye^{x}\Big{|}_{-1}^{1}\right)dy=\int_{0}^{\frac{\pi}{2}}\left(-ey+\frac{y}{e}\right)dy$$
$$=\left(\frac{1}{e}-e\right)\int_{0}^{\frac{\pi}{2}}y~dy=\left(\frac{1}{e}-e\right)\frac{\pi^{2}}{8}$$
en el otro orden de integración
$$\int_{-1}^{1}\left(\int_{0}^{\frac{\pi}{2}}(x\sin(y)-ye^{x})dy\right)dx=\int_{-1}^{1}\left(x\cos(y)-\frac{y^{2}e^{x}}{2}\Big{|}_{0}^{\frac{\pi}{2}}\right)dx=\int_{-1}^{1}\left(-\frac{\pi^{}e^{x}}{8}+x\right)dx$$
$$=\left(\frac{1}{e}-e\right)\frac{\pi^{2}}{8}$$

Se dice que una función $\color{blue}{f(x)}$ es continua en un punto $\color{red}{x_{0}}$ de su dominio, cuando

$$\bbox[5px,border:2px solid red]{\lim_{x\rightarrow \color{red}{x_{0}}}\color{blue}{f(x)}=\color{blue}{f(}\color{red}{x_{0}}\color{blue}{)}}$$

Esto significa, que los puntos «cercanos» a $\color{red}{x_{0}}$ son mandados por $\color{blue}{f}$ cerca de $\color{blue}{f(}$$\color{red}{x_{0}}$$\color{blue}{)}$
Se dice que $\color{blue}{f}$ es continua cuando $\color{blue}{f}$ es continua en cada uno de los puntos de su

$$\bbox[5px,border:2px solid red]{dominio}$$

8 Junio 2016, Creado con GeoGebra

• 
• 
• 

$\framebox[5cm][c]{Medida de Jordan}$
$\textcolor{Blue}{Definición}$
Dado $A\subset \mathbb{R}^{n}$ acotado, definimos $\chi_{A}:\mathbb{R}^{n}\rightarrow \mathbb{R}$, la $\textcolor{Red}{función~ característica}$ de A, de la siguiente forma
$$\boxed{\chi_{A}=\left\{\begin{matrix}
1&si&x\in A\\0&si& x\notin A\end{matrix}\right.}$$

Dado $A\subset \mathbb{R}^{n}$ acotado, decimos que A es $\textcolor{Red}{Jordan Medible} si la función característica de A es integrable sobre algún rectángulo R que contenga a A. En este caso decimos que la medida de Jordan de A (que denotaremos J(A)) esta dada por
$$\boxed{J(A)=\int_{R}\chi_{A}}$$
$\textcolor{Green}{Ejemplo:}$
Sean a,b números positivos y $$A=\left\{(x,y)\in \mathbb{R}^{2}| 0\leq x\leq a, 0\leq y \leq \left(\frac{b}{a}x\right)\right\}$$ En este caso A es un triángulo de base a y altura b. Mostraremos que A es Jordan-Medible en $\mathbb{R}^{2}$, y que su medida es $\frac{ab}{2}$
$\textcolor{Green}{Demostración:}$
Tomemos el rectángulo $R=\{(x,y)\in \mathbb{R}^{2}|0\leq x\leq a, 0\leq y \leq b\}=[0,a]\times[0,b]$ el cual contiene a A. De acuerdo con nuestra definición tenemos que mostar que la función característica $\chi_{A}$ es integrable sobre R y que $$\boxed{\int_{R}\chi_{A}=\frac{ab}{2}}$$
Sea $\displaystyle{P_{1}=\left\{\frac{ia}{n}~|~i=1,…,n\right\}}$ y $\displaystyle{P_{2}=\left\{\frac{ib}{n}~|~i=1,…,n\right\}}$ por tanto $P=P_{1}\times P_{2}$ es una partición del rectángulo R, donde cada subrectángulo tiene medida $\displaystyle{\frac{ab}{n^{2}}}$. Por lo que en este caso
$$\overline{S}(\chi_{A},P)=\sum_{R_{i}\cap A\neq \emptyset}=2\cdot \frac{ab}{n^{2}}+3\cdot \frac{ab}{n^{2}}+…+n\cdot \frac{ab}{n^{2}}=\frac{ab}{n^{2}}\left(\frac{n(n+1)}{2}-1\right)=\frac{ab}{2}\left(1+\frac{1}{n}-\frac{1}{n^2}\right)$$
$$\underline{S}(\chi_{A},P)=\sum_{R_{i}\subset A\neq \emptyset}=1\cdot \frac{ab}{n^{2}}+2\cdot \frac{ab}{n^{2}}+…+(n-1)\cdot \frac{ab}{n^{2}}=\frac{ab}{n^{2}}\left(\frac{(n-1)n}{2}\right)=\frac{ab}{2}\left(1-\frac{1}{n}\right)$$
$\therefore$
$$\lim_{n\rightarrow \infty}\overline{S}(\chi_{A},P)=\lim_{n\rightarrow \infty}\underline{S}(\chi_{A},P)=\frac{ab}{2}$$
$$\boxed{J(A)=\int_{R}\chi_{A}=\frac{ab}{2}}$$

$\textcolor{Green}{Ejemplo:}$
Sea A el conjunto $$A=\left\{(x,y)\in \mathbb{R}^{2}~|~ 0\leq x\leq 1, 0\leq y \leq x^{2}\right\}$$ En este caso A la región de base 1 y altura la función $x^{2}$. Mostraremos que A es Jordan-Medible en $\mathbb{R}^{2}$, y que su medida es $\displaystyle{\frac{1}{3}}$
$\textcolor{Green}{Demostración:}$
Tomemos el rectángulo $R=\{(x,y)\in \mathbb{R}^{2}|0\leq x\leq 1, 0\leq y \leq 1\}=[0,1]\times[0,1]$ el cual contiene a A. De acuerdo con nuestra definición tenemos que mostar que la función característica $\chi_{A}$ es integrable sobre R y que $$\boxed{\int_{R}\chi_{A}=\frac{1}{3}}$$
Sea $\displaystyle{P_{1}=\left\{\frac{ia}{n}~|~i=1,…,n\right\}}$ y $\displaystyle{P_{2}=\left\{\frac{ib}{n}~|~i=1,…,n\right\}}$ por tanto $P=P_{1}\times P_{2}$ es una partición del rectángulo R, donde cada subrectángulo tiene medida $\displaystyle{\frac{1}{n^{2}}}$. Por lo que en este caso
$$\overline{S}(\chi_{A},P)=\sum_{R_{i}\cap A\neq \emptyset}=\frac{1}{n}\cdot \frac{1}{n^{2}}+\frac{1}{n}\cdot \frac{2^{2}}{n^{2}}+…+\frac{1}{n}\cdot \frac{n^{2}}{n^{2}}=\frac{1}{n^{3}}\left(1+2^{2}+\cdots+n^{2}\right)=\frac{1}{n^{3}}\left(\frac{n(n+1)(2n+1)}{6}\right)=\frac{1}{6}\left(1+\frac{1}{n}\right)\left(1+\frac{1}{n}\right)$$
$$\underline{S}(\chi_{A},P)=\sum_{R_{i}\subset A\neq \emptyset}=\frac{1}{n}\cdot \frac{1}{n^{2}}+\frac{1}{n}\cdot \frac{2^{2}}{n^{2}}+…+\frac{1}{n}\cdot \frac{(n-1)^{2}}{n^{2}}=\frac{1}{n^{3}}\left(1+2^{2}+\cdots+(n-1)^{2}\right)=\frac{1}{n^{3}}\left(\frac{(n-1)n(2(n-1)+1)}{6}\right)$$
$$=\frac{1}{6}\left(1-\frac{1}{n}\right)\left(2-\frac{1}{n}\right)$$
$\therefore$
$$\lim_{n\rightarrow \infty}\overline{S}(\chi_{A},P)=\lim_{n\rightarrow \infty}\underline{S}(\chi_{A},P)=\frac{1}{3}$$
$$\boxed{J(A)=\int_{R}\chi_{A}=\frac{1}{3}}$$

$\textcolor{Blue}{Teorema}$
Sea $A\subset\mathbb{R}^{n}$ acotado. Las siguientes afirmaciones son equivalentes:
1.- A es Jordan-Medible
2.-Para cada $\epsilon>0$ existen $R_{1},…,R_{k}$ rectángulos tales que:
(a) $Fr(A)\subset R_{1}\cup\cdots\cup R_{k}$
(b) $\displaystyle{\sum_{i=1}^{k}m(R_{i})<\epsilon}$
3.-La $Fr(A)$ es Jordan-Medible y $J(Fr(A))=0$
$\textcolor{Blue}{Demostración:}$
$(1)\Rightarrow (2)$
Sea $\epsilon>0$. Como A es Jordan-Medible, sabemos que $\chi_{A}$ es integrable sobre un rectángulo que contiene $\overline{A}$ por lo que existe una partición P de R tal que
$$\overline{S}(\chi_{A},P)-\underline{S}(\chi_{A},P)<\epsilon$$
en este caso
$$\overline{S}(\chi_{A},P)=\sum_{R_{i}\cap A\neq0}m(R_{i})$$
$$\underline{S}(\chi_{A},P)=\sum_{R_{i}\subset A}m(R_{i})$$
Por lo que
$$\overline{S}(\chi_{A},P)-\underline{S}(\chi_{A},P)=\sum_{R_{i}\cap A\neq \emptyset\atop{R_{i}\cap A^{c}\neq \emptyset}}m(R_{i})$$
Para ver que
$$Fr(A)\subset R_{1}\bigcup\cdots\bigcup R_{k}$$
Como $\underline{A}\subset int(R)$ entonces $Fr(A)\subset int(R)$. Sea $x\in Fr(A)$, si $x\in int(R_{i})$ entonces la condición se cumple
Si $x\notin int(R)$ entonces esta en la frontera de más de uno de los subrectángulos por lo que
(1) Si los subrectángulos estan en $int(A)$ entonces $x\in int(A)$
(2) Si los subrectángulos estan en $int(A^{c})$ entonces $x\in ext(A)$
En ambas situaciones $x\notin Fr(A)$ lo cual es una contradicción.
Por lo tanto $x\in R_{i}$ donde $R_{i}$ cumple la condición pedida.
$(2)\Rightarrow (3)$
Para probar que $Fr(A)$ es Jordan-Medible, se tiene que probar que $\chi_{A}$ es integrable sobre el rectángulo R ya que $Fr(a)\subset R$.
Como existen $R_{1},…,R_{k}$ rectángulos tales que:
\begin{align*}
(a)&Fr(A)\subset R_{1}\bigcap\cdots\bigcap R_{k}\\
(b)&\sum_{i=1}^{k}m(R_{i})<\epsilon
\end{align*}
Entonces
$$\overline{S}(\chi_{Fr(A)},P)=\sum_{R_{i}\cap A\neq\emptyset\atop{R_{i}\cap A^{c}\neq\emptyset}}m(R_{i})<\epsilon$$
Y como
$$\underline{S}(\chi_{Fr(A)},P)\leq \overline{S}(\chi_{Fr(A)},P)<\epsilon$$
entonces
$$0\leq \sup\{\underline{S}(\chi_{Fr(A)},P)\}<\epsilon$$
$$0\leq \inf\{\overline{S}(\chi_{Fr(A)},P)\}<\epsilon$$
entonces
$$\int_{R}\chi_{Fr(a)}=\overline{\int}_{R}\chi_{Fr(A)}=\underline{\int}_{R}\chi_{Fr(A)}=0$$
$(3)\Rightarrow (1)$
Como $Fr(A)$ es Jordan-Medible y $J(Fr(A))=0$, existe una partición P tal que $Fr(A)\cap R_{i}\neq\emptyset$ entonces
$$\overline{S}(\chi_{Fr(A)})=\sum_{R_{i}\cap Fr(A)\neq \emptyset}m(R_{i})<\epsilon$$
Por lo tanto
$$\overline{S}(\chi_{Fr(A)})-\underline{S}(\chi_{Fr(A)})=\sum_{R_{i}\cup A\neq\emptyset\atop{R_{i}\cup A^{c}\neq\emptyset}}m(R_{i})\leq \sum_{R_{i}\cup Fr(A)\neq\emptyset}m(R_{i})<\epsilon$$
por lo tanto $\chi_{A}$ es integrable sobre R y en consecuencia A es un conjunto Jordan-Medible.$~~\blacksquare$

$\textcolor{Blue}{Teorema}$
Sea $f:R\subset\mathbb{R}\rightarrow\mathbb{R}$ acotada sobre el rectángulo R. Si el conjunto de discontinuidades de f en R $(D_{f,R})$ es un conjunto Jordan-Medible y de Medida cero entonces f es integrable sobre R.
$\textcolor{Blue}{Demostración}$
Sea $M>0$ tal que $|f(\widehat{x})|\leq M$ para todo $\widehat{x}\in R$.
Sea $\epsilon>0$. Dado que $J(D_{f,R})=0$ sabemos que existe una partición P de R tal que
$$\overline{S}(\chi_{D_{f,R}},P)<\frac{\epsilon}{4M}$$
Si $R_{1},…,R_{l}$ son los subrectángulos de R inducidos por la partición P que tienen la propiedad de que $R_{i}\cap D_{f,R}\neq\emptyset~~(i=1,2,…,l)$, tenemos entonces que
$$\sum_{i=1}^{l}m(R_{i})<\frac{\epsilon}{4M}$$
Si $R_{\ell+1},…,R_{k}$ son el resto de los subrectángulos de R inducidos por P, sabemos que f es continua en cada uno de ellos por tanto f es integrable sobre cada $R_{i}~~(i=\ell+1,…,k)$. Para cada uno de estos subrectángulos podemos encontrar una partición $P^{(i)}$ tal que
$$\overline{S}(f,P^{(i)})-\underline{S}(f,P^{(i)})<\frac{\epsilon}{2(k-\ell)}$$
Para cada $i=\ell+1,…,k$. Cada una de estas particiones $P^{(i)}$ la extendemos a todo el rectángulo R y junto con la partición inicial P, formamos una nueva partición del rectángulo R a la que llamaremos Q.
si los subrectángulos inducidos por Q los denotamos $R^{‘}_{j,i}$, en donde $(i=1,…,k)$ y $(j=1,..k_{i})$, entonces
$$R_{i}=\bigcup_{j=1}^{k_{i}}R’_{j,i}$$
Observe que para $i=\ell+1,…,k$ los $R’_{j,i}$ $(j=1,…,k_{i})$ son subrectángulo de $R_{i}$ inducidos por alguna partición $Q^{(i)}$ que refina a $P^{(i)}$ de modo tal que
\begin{align*}
\overline{S}(f,Q^{(i)})-\underline{S}(f,Q^{i})&\leq \overline{S}(f,P^{(i)})-\underline{S}(f,P^{i})\\
&<\frac{\epsilon}{2(k-\ell)}
\end{align*}
Tenemos que
\begin{align*}
\overline{S}(f,Q)-\underline{S}(f,Q)&=\sum_{i=1}^{k}\left(\sum_{j=1}^{k}(M’_{j,i}-m’_{j,i})\cdot m(R’_{j,i}\right)\\
&=\sum_{i=1}^{k}\left(\sum_{j=1}^{k}(M’_{j,i}-m’_{j,i})\cdot m(R’_{j,k}\right)+\sum_{i=\ell+1}^{k}\left(\sum_{j=1}^{k}(M’_{j,i}-m’_{j,i})\cdot m(R’_{j,k}\right)\\
&=\sum_{i=1}^{\ell}\left(\sum_{j=1}^{k_{i}}(M’_{j,i}-m’_{j,i})\cdot m(R’_{j,k}\right)+\sum_{i=\ell+1}^{k}\left(\overline{S}(f,Q^{i})-\underline{S}(f,Q^{i})\right)\\
&\leq \sum_{i=1}^{\ell}\left(\sum_{j=1}^{k_{i}}2M\cdot m(R’_{j,i})\right)+\sum_{i=\ell+1}^{k}\left(\overline{S}(f,P^{i})-\underline{S}(f,P^{i})\right)\\
&<2M\cdot \sum_{i=1}^{\ell}\left(\sum_{j=1}^{k_{i}} m(R’_{j,i})\right)+\sum_{i=\ell+1}^{k}\frac{\epsilon}{2(k-\ell)}\\
&=2M\cdot \sum_{i=1}^{\ell}m(R_{i})+\frac{\epsilon}{2}\\
&<2M\cdot \left(\frac{\epsilon}{4M}\right)+\frac{\epsilon}{2}\\
&=\epsilon
\end{align*}
En donde, como era de esperarse, $M’_{j,i}=\sup\{f(\widehat{x})~|~\widehat{x}\in R’_{j,i}\}$ y $m’_{j,i}=\inf\{f(\widehat{x})~|~\widehat{x}\in R’_{j,i}\}$ para $i=1,…,k$ y $j=1,…,k_{i}$.$~~\blacksquare$

Si $f:A\subset\mathbb{R}^{2}\rightarrow \mathbb{R}$. Denotamos por $D_{fA}$ al conjunto de discontinuidades de f en A, es decir
$$D_{fA}=\{x\in A~|~f~es~discontinua~en~x\}$$

$\textcolor{Blue}{Proposición}$: Sea $f:A\subset\mathbb{R}^{2}\rightarrow \mathbb{R}$ integrable sobre R. Entonces $D_{fR}$ tiene interior vacio $int~D_{fR}=\emptyset$
$\textcolor{Blue}{Demostración}$: Si $int~D_{fR}\neq\emptyset$ entonces existe $R’$ tal que $R’\subset int(D_{fR})\subset D_{fR}\subset R$
como f es integrable sobre R y $R’\subset R$ entonces f es integrable sobre $R’$ de modo que existe $x_{0}\in int(R’)$ tal que f es continua en $x_{0}$ lo cual contradice el hecho de que f es discontinua en todo $x\in D_{fR}$.$~~\blacksquare$

Medida Cero y Contenido Cero
$\textcolor{Blue}{Definición}$: Un subconjunto $A\subset\mathbb{R}^{n}$ tiene medida cero si para cada $\epsilon>0$ existe un recubrimiento ${U_{1},U_{2},…}$ de A por rectángulos tales que
$$A\subset \bigcup_{i=1}^{\infty}U_{i}~~y~~\sum_{i=1}^{\infty}v(U_{i})<\epsilon$$
Por ejemplo un conjunto formado por un número finito de puntos claramente tiene medida cero

Si A tiene infinitos puntos que pueden ordenarse formando una sucesión $a_{1},a_{2},…$ entonces A tiene medida cero, pues para cada $\epsilon>0$ se puede elegir $U_{i}$ que sea rectángulo cerrado que contenga $a_{i}$ con $\displaystyle{v(U_{i})<\frac{\epsilon}{2^{i}}}$.
Entonces$$\sum_{i=1}^{\infty}v(U_{i})<\sum_{i=1}^{\infty}\frac{\epsilon}{2^{i}}=\epsilon\sum_{i=1}^{\infty}\frac{1}{2^{i}}=\epsilon\left(\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+…\right)=\frac{\epsilon}{2}\left(1+\frac{1}{2}+…\right)=$$
$$\frac{\epsilon}{2}\left(\frac{1}{1-\frac{1}{2}}\right)=\frac{\epsilon}{2}(2)=\epsilon$$

$\textcolor{Green}{Ejemplo}$: $\mathbb{Q}$ es de medida cero.
$\textcolor{Green}{Demostración}$: Como $\mathbb{Q}$ es numerable podemos formar $\displaystyle{\left\{r_{k}\right\}^{\infty}_{1}}$ y dado $\epsilon>0$, sea $$I_{k}=\left(r_{k}-\frac{\epsilon}{2^{k+2}},r_{k}+\frac{\epsilon}{2^{k+2}}\right)$$Por lo que $$\mathbb{Q}\subset \bigcup_{k=1}^{\infty} I_{k}\quad y \quad v(I_{k})=\frac{\epsilon}{2^{k+1}}$$y para la suma de los volumenes se tiene
$$\sum_{k=1}^{\infty}\frac{\epsilon}{2^{k+1}}=\frac{\epsilon}{4}\left(1+\frac{1}{2}+…\right)=\frac{\epsilon}{2}<\epsilon$$
$\therefore$ $\mathbb{Q}$ tiene medida cero.$~~\blacksquare$

$\textcolor{Green}{Ejemplo}$: El conjunto de Cantor
$\textcolor{Green}{Demostración}$: Tenemos que
\begin{align} \mathcal{C}_{0} &=[0,1]\\ \mathcal{C}_{1}&= \left[0,\frac{1}{3}\right] \cup \left[\frac{2}{3},1\right]\\ \mathcal{C}_{2}&= \left[0,\frac{1}{9}\right] \cup \left[\frac{2}{9},\frac{1}{3}\right]\cup \left[\frac{2}{3},\frac{7}{9}\right]\ \cdot\ \cdot\ \cdot\ \mathcal{C}{n}=\left[0,\frac{1}{3^{n}}\right]\cup \cdot \cdot \cdot \cup \left[1-\frac{1}{3^{n}},1\right]
\end{align}
Tenemos que $\displaystyle{\mathcal{C}=\bigcap_{k=0}^{\infty}\mathcal{C}_{k}}$ (Conjunto de Cantor).
Cada $\mathcal{C}_{k}$ es la unión de $2^{k}$ intervalos de longitud $\displaystyle{\frac{1}{3^{k}}}$ si los llamamos $I{1}, I_{2},…,I_{2^{k}}$ entonces
$$\mathcal{C}\subset \mathcal{C}_{k}=\bigcup{i=1}^{2^{k}}I_{i} \quad y \quad \sum_{i=1}^{2^{k}}vol(I_{i})=\left(\frac{2}{3}\right)^{k}$$
por lo que dado $\epsilon>0$ podemos tomar $k$ tal que $\displaystyle{\left(\frac{2}{3}\right)^{k}<\epsilon}$. Entonces $\mathcal{C}$ es de medida cero.$\blacksquare$

$\textcolor{Green}{Ejemplo}$: En $\mathbb{R}^{2}$ consideramos la recta $y=y_{0}$
$\textcolor{Green}{Demostración}: La semirecta derecha $A={(x,y_{0})| x\in \mathbb{R}}$ la cubrimos con $$R_{k}=\left[k,k+1\right]\times \left[y_{0}-\frac{\epsilon}{2^{k+3}},y_{0}+\frac{\epsilon}{2^{k+3}}\right]$$ con $k\in \mathbb{N}\cup {0}$ y $$v(R_{k})=1\cdot \left(\frac{\epsilon}{2^{k+2}}\right)\Rightarrow \sum_{k=1}^{\infty}\frac{\epsilon}{2^{k+2}}=\frac{\epsilon}{2}<\epsilon$$
Mientras que para la semirecta izquierda consideramos $$R_{k}=\left[-k-1,-k\right]\times \left[y_{0}-\frac{\epsilon}{2^{k+3}},y_{0}+\frac{\epsilon}{2^{k+3}}\right]$$
$\therefore$
$$v(R_{k})=1\cdot \left(\frac{\epsilon}{2^{k+2}}\right)\Rightarrow \sum_{k=1}^{\infty}\frac{\epsilon}{2^{k+2}}=\frac{\epsilon}{2}<\epsilon$$
$\therefore$ la recta entera se puede cubrir con una unión numerable de rectángulos cuya suma es menor a $\epsilon$.$\blacksquare$

$\textcolor{Green}{Ejemplo}$: Los intervalos cerrados $[a,b]\subset \mathbb{R}$ con $a<b$ no tienen medida cero.
$\textcolor{Green}{Demostración}$: Supongamos que $[a,b]\subset \bigcup_{n=1}^{\infty}U_{n}$ con $U_{n}$ abierto, como $[a,b]$ es compacto existe una subcubierta finita ${U_{n}}$ con $$\sum_{k=1}^{\infty} v(U_{k})<\epsilon \quad pero \quad \sum_{k=1}^{\infty} v(U_{k})\geq b-a$$ lo cual nos dice que la suma de volumenes no se puede hacer tan pequeña como se desee, por lo que el conjunto dado no es de medida cero.$\blacksquare$

$\textcolor{Blue}{Teorema}$: Si $A=A_{1}\bigcup A_{2}\bigcup …$ y cada $A_{i}$
tiene medida cero, entonces A tiene medida cero.
$\textcolor{Blue}{Demostración}$: Sea $\epsilon>0$. Puesto que cada $A_{i}$ tiene medida cero
$\exists$ un recubrimiento ${U_{i1},U_{i2},…}$ de $A_{i}$ por
rectángulos cerrados tales que la colección de todos los $U_{ij}$
cubren a A y formamos la sucesión numerable $$U_{11},U_{1,2},…$$
$\therefore$
$$\sum_{j=1}^{\infty}v(U_{ij})<\sum_{i=1}^{\infty}\frac{\epsilon}{2^{i}}<\epsilon~\blacksquare$$

$\textcolor{Blue}{Definición}$: Un subconjunto A de $\mathbb{R}^{n}$ tiene contenido cero si para cada $\epsilon>0$ existe un recubrimiento finito ${U_{1},U_{2},…,U_{n}}$ de A por rectángulos tales que $$\sum_{i=1}^{n}v(U_{i})<\epsilon$$

$\textcolor{Blue}{Teorema}$: Si A es compacto y tiene medida cero, entonces A
tiene contenido cero.
$\textcolor{Blue}{Demostración}$: Sea $\epsilon>0$. Puesto que $A$ tiene medida cero,$\exists$ un recubrimiento ${U_{1},U_{2},…}$ de $A$ por rectángulos tales que $\displaystyle{\sum_{i=1}^{\infty}v(U_{i})<\epsilon}$. Dado que A es compacto, un
número finito de ${U_{1},U_{2},…,U_{n}}$ recubren a A y ademas
$\displaystyle{\sum_{i=1}^{n}v(U_{i})<\epsilon}~~\blacksquare$

$\textcolor{Blue}{Teorema}$: Sea $\phi:[a,b]\rightarrow\mathbb{R}$ una función continua. Entonces la gráfica de $\phi$ tiene contenido cero.
$\textcolor{Blue}{Demostración}$: Siendo $\phi$ continua en el compacto $[a,b]$, es
uniformemente continua en dicho intervalo. Es decir dado $\epsilon>0\quad\exists\quad\delta>0$ tal que para $x,y\in[a,b]$ si
$|x-y|<\delta\quad\Rightarrow\quad|f(x)-f(y)|<\frac{\epsilon}{b-a}$.
Sea $n\in\mathbb{N}$ tal que $\frac{b-a}{n}<\delta$ y consideremos
la partición de $[a,b]$ en n partes iguales
$$a=x_{0}<x_{1}<…<x_{n}=b$$ con $x_{i}=a+i\frac{b-a}{n}$ se tiene
entonces que para
$x,y\in[x_{i-1},x_{i}]\Rightarrow|f(x)-f(y)|<\frac{\epsilon}{b-a}$
$\therefore$
$$\sum_{i=1}^{n}(x_{i}-x_{i-1})\frac{\epsilon}{b-a}=\frac{\epsilon}{b-a}\sum_{i=1}^{n}(x_{i}-x_{i-1})=\frac{\epsilon}{b-a}(b-a)=\epsilon~~\blacksquare$$

$\textcolor{Blue}{Teorema}$: Sea R un rectángulo cerrado y $f:R\rightarrow
\mathbb{R}$ una función acotada. Sea $B=\{x\in\mathbb{R}|f\quad
no\quad es \quad continua\quad en\quad x\}$ entonces si B es un
conjunto de contenido cero f es integrable.
$\textcolor{Blue}{Demostración}$: Vamos a dividir los subrectángulos $R_{ij}$ en
$I)R_{ij}\bigcap B\neq\emptyset$ y $II)R_{ij}\bigcap B=\emptyset$
de manera que para los rectángulos I se tiene que B es de contenido cero $\therefore$
$$\sum_{i=1}^{m}\sum_{j=1}^{n}v(R_{ij})<\epsilon$$ Mientras que para
los rectángulos II se tiene que f es continua y por tanto
$$\sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}-m_{ij}A(R_{ij})<\sum_{i=1}^{m}\sum_{j=1}^{n}\frac{\epsilon}{2A(R)}A(R_{ij})$$
$\therefore$ Dada la partición P de R se tiene que
$$\overline{S}(f,P)-\underline{S}(f,P)=\sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}-m_{ij}A(R_{ij})+\sum_{i=1}^{m}\sum_{j=1}^{n}v(R_{ij})<\sum_{i=1}^{m}\sum_{j=1}^{n}\frac{\epsilon}{2A(R)}A(R_{ij})+\frac{\epsilon}{2}$$
$$=\frac{\epsilon}{2A(R)}A(R_{ij})\sum_{i=1}^{m}\sum_{j=1}^{n}A(R_{ij})+\frac{\epsilon}{2}=\frac{\epsilon}{2A(R)}A(R)+\frac{\epsilon}{2}=\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon~\blacksquare$$

$\textcolor{Blue}{Teorema}$: Sea f una función definida en un rectángulo R. Si el conjunto S de puntos donde f es discontinua tiene contenido cero, entonces f es integrable sobre R.

$\textcolor{Blue}{Demostración}$: Sea $\epsilon>0$ dado y sea $\textcolor{Red}{R_{1},R_{2},…,R_{k}}$ el conjunto de rectángulos que cubren a S

tal que
$$\sum_{i=1}^{k}A(R_{i})<\epsilon$$
si se colocan sobre cada $\textcolor{Red}{R_{j}}$ un rectángulo $\textcolor{Green}{R’_{j}}$ con el mismo centro pero del doble de dimensiones

se tiene que
$$\sum_{i=1}^{k}A(\textcolor{Green}{R’{i}})=\sum{i=1}^{k}4A(\textcolor{Red}{R_{i}})<4\epsilon$$
Además, entre los rectángulos $\textcolor{Red}{R_{j}}$ habrá un lado más corto. Denotemos su longitud por $2r$

si tomo el conjunto $R’$ el resto de R después que se han eliminado los interiores de los $\textcolor{Red}{R_{j}}$.

Se tiene que sobre $R’$ f es continua y por tanto uniformemente continua por lo tanto
$$|f(p)-f(q)|<\epsilon~si~|p-q|<\delta$$para cualesquiera p,q en $R’$\Sea $P$ una partición de R tal que $|P|<\delta<r$

Vamos a estimar
$$\overline{S}(f,P)-\underline{S}(f,P)$$
Para esto dividimos los rectángulos de la partición P en dos conjuntos
$$\textcolor{Green}{R'{j}}\bigcap \textcolor{Red}{R{j}}\neq\emptyset~~~~\textcolor{Green}{R'{j}}\bigcap \textcolor{Red}{R{j}}=\emptyset$$
se tiene entonces que
$$\overline{S}(f,P)-\underline{S}(f,P)=\sum_{i=1}^{n}\sum_{j=1}^{m}(M_{ij}-m_{ij})A(R_{ij})=$$
$$\left(\sum\sum(M_{ij}-m_{ij})A(R_{ij})\right){\textcolor{Green}{R'{j}}\bigcap \textcolor{Red}{R_{j}}\neq\emptyset}+\left(\sum\sum(M_{ij}-m_{ij})A(R_{ij})\right){\textcolor{Green}{R'{j}}\bigcap \textcolor{Red}{R_{j}}=\emptyset}<4M\epsilon+\epsilon A=\epsilon(4M+A)$$
donde $M=\sup{f(x)}$ sobre R.$~\blacksquare$

Sumas superiores y sumas inferiores

Denotaremos por $\underline{S}(f)$ al conjunto de todas las sumas inferiores de una función f (Definida sobre el rectángulo R) y como $\overline{S}(f)$ al conjunto de todas las sumas inferiores es decir
$$\underline{S}(f)=\{\underline{S}(f,P)~|~P~\in~P_{R}\}$$
$$\overline{S}(f)=\{\overline{S}(f,P)~|~P~\in~P_{R}\}$$
Definición: Al supremo del conjunto $\underline{S}(f)$ lo
llamamos integral inferior de f sobre R y se puede denotar $\displaystyle{\underline{\int}(f)}$. Y al ínfimo del conjunto $\overline{S}(f)$ lo llamamos integral superior de f sobre R y se puede denotar $\displaystyle{\overline{\int}(f)}$.
Definición: Sea $f:R\subset\mathbb{R}^{n}\rightarrow\mathbb{R}$ acotada sobre el
rectángulo R. Decimos que f es integrable según Riemann sobre R si se tiene que la integral inferior y la integral superior de f sobre R son iguales. Es decir $$\underline{\int}R_{f}=\overline{\int}R_{f}$$ En este caso, a
este número lo llamaremos la integral de f y lo denotarremos por
$$\int\int_{R}f$$
Lema: Para cada $\epsilon>0$ existe una partición P de R tal que
$$0\leq \underline{\int}{R}f-\underline{S}(f,p)<\epsilon~~y~~0\leq \overline{S}(f,p)-\overline{\int}{R}f<\epsilon$$
Demostración:

Como
$$\underline{\int}{R}(f)=\sup{\underline{S}(f)}~ \exists~ P_{1}\in~P_{R}~tal~que$$
$$\underline{\int}{R}(f)-\sup{\underline{S}(f)}<\epsilon$$ $$\overline{\int}{R}(f)=\inf{\overline{S}(f)}~\exists~ P_{2}\in~P_{R}~ tal~que$$
$$\inf{\overline{S}(f)}-\underline{\int}{R}(f)<\epsilon$$ Sea $P=P{1}\bigcup P_{2}$ se tiene entonces que
$$\overline{S}(f,P)\leq \overline{S}(f,P_{2})-\underline{S}(f,P_{1})\leq \underline{S}(f,P)$$
por lo tanto
$$0\leq \underline{\int}{R}f-\underline{S}(f,P)\leq \underline{\int}{R}f-\underline{S}(f,P_{1})<\epsilon$$
$$0\leq \overline{S}(f,P)-\overline{\int}{R}f\leq \underline{S}(f,P{2})-\underline{\int}_{R}f<\epsilon~~\blacksquare$$
Teorema: Sea $f:R\subset\mathbb{R}^{n}\rightarrow\mathbb{R}$ acotada sobre el rectángulo R. Se tiene que f es integrable sobre R si y solo si para cada $\epsilon>0$ existe una P partición de R tal que $$\overline{S}(f,P)-\underline{S}(f,P)<\epsilon$$
Demostración: Sea $\epsilon>0$ como f es integrable $\underline{\int}{R}f=\overline{\int}{R}f=I$ y por las propiedades del supremo sabemos que para $\displaystyle{\frac{\epsilon}{2}>0}$ $\exists$ una $P\prime$ partición de R tal que
$$I-\frac{\epsilon}{2}\leq\underline{S}(f,P\prime)\leq I.$$ Por otra parte de las propiedades del ínfimo sabemos que $\exists$ una $Q\prime$ partición de R tal que
$$I\leq\overline{S}(f,Q\prime)\leq I+\frac{\epsilon}{2}.$$ Si hacemos $P=P\prime\bigcup Q\prime$ tenemos que $$\underline{S}(f,P\prime)\leq\underline{S}(f,P)\leq\overline{S}(f,P)\leq\overline{S}(f,P\prime)$$
$\therefore$
$$I-\frac{\epsilon}{2}\leq\underline{S}(f,P)\leq\overline{S}(f,P)\leq I+\frac{\epsilon}{2}$$
$\therefore$
$$\overline{S}(f,P)-\underline{S}(f,P)\leq I+\frac{\epsilon}{2}-(I-\frac{\epsilon}{2})=\epsilon.$$
$\therefore$ f es integrable.

$(\Leftarrow)$ Tenemos que probar que la función es integrable es decir $\displaystyle{\underline{\int}{R}f=\overline{\int}{R}f}$ o equivalentemente
$\displaystyle{\underline{\int}{R}f-\overline{\int}{R}f=0}$ sabemos que
$$\underline{\int}{R}f\leq\overline{\int}{R}f\Rightarrow
0\leq\overline{\int}{R}f-\underline{\int}{R}f.$$ Sea $\epsilon>0$
por hipótesis, existe P partición de R tal que
$\overline{S}(f,P)-\underline{S}(f,P)<\epsilon$ por otra parte se
tiene que:
$$\underline{S}(f,P)\leq\underline{\int}{R}f\leq\overline{\int}{R}f\leq\overline{S}(f,P)$$
$\therefore$
$$0\leq\overline{\int}{R}f-\underline{\int}{R}f\leq\overline{S}(f,P)-\underline{S}(f,P)<\epsilon$$
$\therefore$
$$\overline{\int}{R}f=\underline{\int}{R}f$$ $\therefore$ f es
integrable. $\blacksquare$
Teorema: Si una función f es continua en un rectángulo $Q=[a,b]\times[c,d]$ entonces
f es integrable en Q.
Demostración: Tenemos que
$$\overline{S}(f,P)-\underline{S}(f,P)=\sum_{i=1}^{m}\sum_{j=1}^{n}M_{ij}\Delta (R_{ij})-\sum_{i=1}^{m}\sum_{j=1}^{n}m_{ij}\Delta (R_{ij})=\sum_{i=1}^{m}\sum_{j=1}^{n}(M_{ij}-m_{ij})\Delta (R_{ij})$$
$$\sum_{i=1}^{m}\sum_{j=1}^{n}\frac{\epsilon}{A(R)}\Delta (R_{ij})=\frac{\epsilon}{A(R)}\sum_{i=1}^{m}\sum_{j=1}^{n}\Delta (R_{ij})=\frac{\epsilon}{A(R)}A(R)$$
La desigualdad se justifica de la siguiente forma: Como f es continua en un conjunto cerrado y acotado entonces f es uniformemente continua $\therefore$ para $$\overline{x_{ij}},\overline{y_{ij}}\in R_{ij}~con~~~|x_{ij}-y_{ij}|<\delta\Rightarrow
|f(x_{ij})-f(y_{ij})|<\frac{\epsilon}{A(R)}~~\blacksquare$$
Ejemplo: Si f es una función integrable sobre R y $R_{k}\subset R$ entonces f es integrable sobre $R_{k}$
Demostracion: Como f es integrable sobre R existe una partición P de R tal que
$$\overline{S}(f,P)-\underline{S}(f,P)<\epsilon$$
Sean $P_{1}$ los $R_{i,j}\in P$ tal que $R_{ij}\subset R_{k}$ y sea $P_{2}$ los $R_{ij}$ restantes, tenemos entonces que
$$\overline{S}(f,P)=\overline{S}(f,P_{1})+\overline{S}(f,P_{2})$$
$$\underline{S}(f,P)=\underline{S}(f,P_{1})+\underline{S}(f,P_{2})$$
por lo tanto
$$\overline{S}(f,P_{1})-\underline{S}(f,P_{1})+\overline{S}(f,P_{2})-\underline{S}(f,P_{2})=\overline{S}(f,P)-\underline{S}(f,P)<\epsilon$$
como cada término de la suma es positivo se tiene que
$$\overline{S}(f,P_{1})-\underline{S}(f,P_{1})<\epsilon$$
y tenemos una partición de $R_{k}\subset R$ donde f es integrable.$~~\blacksquare$
Teorema: Sea $f:R\subset\mathbb{R}^{2}\rightarrow \mathbb{R}$ integrable sobre R. Entonces existe $x_{0}\in~int (R)$ tal que f es continua en $x_{0}$
Demostración: Como f es integrable sobre R existe una partición P de R tal que
$$\overline{S}(f,P)-\underline{S}(f,P)=\sum_{i=1}^{n}\sum_{j=1}^{m}(M_{ij}-m_{ij})A(R)<A(R)$$ como los sumandos son términos no negativos, existen subíndices $ij_{1}$ tal que $M_{ij_{1}}-m_{ij_{1}}<1$ pues de lo contrario si
$$M_{ij}-m_{ij}\geq1~\forall i,j~~\Rightarrow~(M_{ij}-m_{ij})A(R_{ij})\geq A(R_{ij})~\Rightarrow~\sum_{i=1}^{n}\sum_{j=1}^{m}(M_{ij}-m_{ij})A(R_{ij})\geq \sum_{i=1}^{n}\sum_{j=1}^{m}(R_{}ij)=A(R)$$ lo cual contradice nuestra suposición.
Ahora bien sea $R_{ij_{1}}$ el subrectángulo de la partición P que cumple $M_{ij_{1}}-m_{ij_{1}}<1$ donde $R_{ij_{1}}\subset R$.
Como f es integrable sobre R y $R_{ij_{1}}\subset R$ entonces f es integrable en $R_{ij_{1}}$, existe entonces una partición $P_{1}$ de $R_{ij_{1}}$
tal que
$$\overline{S}(f,P_{1})-\underline{S}(f,P_{1})=\sum_{i=1}^{n_{1}}\sum_{j=1}^{m_{1}}(M_{ij_{1}}-m_{ij_{1}})A(R_{ij_{1}})<\frac{A(R_{ij_{1}})}{2}$$Podemos asegurar que existe un subrectángulo $R_{ij_{2}}$ inducido por $P_{1}$ con la propiedad $\displaystyle{M_{ij_{2}}-m_{ij_{2}}<\frac{1}{2}}$ donde
$$M_{ij_{2}}=\sup\{f(x)~|~x\in R_{ij_{2}}\}~~~m_{ij_{2}}=\inf\{f(x)~|~x\in R_{ij_{2}}\}$$ y además $R_{ij_{2}}\subset R_{ij_{1}}$.

Siguiendo este procedimiento, obtenemos una sucesión de rectángulos ${R_{ij_{k}}}$ anidados en $\mathbb{R}^{2}$ con la propiedad
$$M_{ij_{k}}-m_{ij_{k}}<\frac{1}{k}~donde~M_{ij_{k}}=\sup\{f(x)~|~x\in R_{ij_{k}}\}~m_{ij_{k}}=\inf\{f(x)~|~x\in R_{ij_{k}}\}~R_{ij_{k+1}}\subset R_{ij_{k}}$$

Sabemos que
$$\bigcap_{k=1}^{\infty}R_{ij_{k}}\neq\emptyset$$
Ahora, si $$x_{0}\in\bigcap_{k=1}^{\infty}R_{ij_{k}}$$ vamos a comprobar que f es continua en $x_{0}$. Sea $\epsilon>0$ y $N\in\mathbb{N}$ tal que $\displaystyle{\frac{1}{N}<\epsilon}$. Como $x_{0}\in R_{ij_{N+1}}\subset R_{ij_{N}}$ existe un $\delta>0$ tal que
$$B_{\delta}(x_{0})\subset R_{ij_{N}}$$ de tal forma que
$$m_{ij_{N}}\leq f(x)\leq M_{ij_{N}}~\forall x\in B_{\delta}(x_{0})$$ como $\displaystyle{M_{ij_{N}}-m_{ij_{N}}<\frac{1}{N}}$ se tiene que
$$|f(x)-f(x_{0})|<\frac{1}{N}<\epsilon~\forall x\in B_{\delta}(x_{0})$$por lo tanto f es continua en $x_{0}$.$~~\blacksquare$
Ejercicio:Sea $f:R\subset\mathbb{R}^{2}\rightarrow \mathbb{R}$ integrable sobre R tal que $f(x)\geq0$ $\forall~x\in~R$. Si f es continua en $x_{0}\in R$ y $f(x_{0})>0$ entonces $$\int_{R}f>0$$
Solución: Si f es continua en $x_{0}\in R$ y $f(x_{0})>0$ $\exists~\delta>0$ tal que
$$|f(x)-f(x_{0})|<\frac{f(x_{0})}{2}$$ por lo tanto $$\frac{f(x_{0})}{2}0$$
por lo tanto
$$0<\underline{S}(f,P)\leq\int_{R}f~~\blacksquare$$