Curvas parametrizadas

Sea $$ \alpha (t) = (x(t), y(t), z(t))$$ una curva, donde $t$ es el tiempo y $(x(t), y(t), z(t))$ la posición en el espacio.

Es decir, para cada $t$ tenemos que:

$$t \longrightarrow (x(t), y(t), z(t))$$

Y la curva representa el camino que describe.

La derivada de $\alpha (t)$ está dada por:

$$ {\alpha}’ (t) = ({x}'(t), {y}'(t), {z}'(t))$$

$${\alpha}’ (t) = \lim_{\Delta t \to \infty} \dfrac{(\alpha (t_0 \, – \, \Delta t) \, – \, \alpha (t_0))}{\Delta t} $$

Y representa la velocidad instantánea.

La rapidez es $\|{\alpha}’ (t) \|.$

Además, la aceleración instantánea está dada por $${\alpha}^{\prime \prime} (t)$$

Movimiento rectilíneo uniforme

Dado el punto $\vec{p_0} (x_0, y_0, z_0)$ que representa la posición inicial.

El vector velocidad constante, está dado por $\vec{v} = (v_1, v_2, v_3).$

Por lo que, la curva que representa el camino que se describe es: $$ \alpha (t) = \vec{p_0} + \vec{v}(t)$$ $$ \alpha (t) = (x_0, y_0, z_0) +t(v_1, v_2, v_3)$$ $$ \alpha (t) = (x_0 + t v_1, y_0 + t v_2, z_0 + t v_3)$$

La ecuación de la recta tangente es: $$\beta (t) = \alpha (t_0) + t {\alpha}’ (t_0)$$

Existe una recta tangente si ${\alpha}’ (t_0) \neq \vec{0}$.

Si ${\alpha}’ (t_0) = \vec{0}$, estamos diciendo que la velocidad es $0$, es decir, no se mueve, y por tanto $\alpha (t) = \vec{p_0}$ para toda $t.$

Los puntos donde ${\alpha}’ (t_0) = 0$ son excepcionales.

${}$

Haz click en la imagen para ver una animación de la parametrización.

Curvatura de una curva

La curvatura de una curva $\alpha : [a,b] \subset \mathbb{R} \rightarrow \mathbb{R}^n$ en un punto $\alpha(t_0)$ es la curvatura de la circunferencia osculatriz (osculadora), «la que más se parece a la curva cerca del punto».

• ¿Cuál es la curvatura de una circunferencia?

• De todas las circunferencias que pasan por el punto, ¿cuál es la que más se parece a la curva?

Definamos la curvatura de una circunferencia de radio $r$ como el número $\textcolor{RoyalBlue}{\mathcal{K} = \frac{1}{r}}$

Observación «física»:

Supongamos que tenemos una circunferencia parametrizada con rapidez constante 1.

$\alpha (s)$ nos da la posición.

${\alpha}’ (s)$ nos da la velocidad.

${\alpha}^{\prime \prime} (s)$ nos da la aceleración.

$\big\| {\alpha}’ (s) \big\| = 1$

$\big\| {\alpha}’ (s) \big\|^2 = 1$ constante.

Como la aceleración es perpendicular a la velocidad, se cumple que $ \big\langle {\alpha}’ (s) , {\alpha}^{\prime \prime} (s) \big\rangle = 0$

$ \big\langle {\alpha}’ (s) , {\alpha}’ (s) \big\rangle \equiv 1$ derivando $ \big\langle {\alpha}^{\prime \prime} (s) , {\alpha}’ (s) \big\rangle + \big\langle {\alpha}’ (s) , {\alpha}^{\prime \prime} (s) \big\rangle \equiv 0$

¿Cuál es la relación que hay entre $\mathcal{K}$ y ${\alpha}^{\prime \prime} (s)$ ?

Circunferencia de radio $1$ parametrizada con rapidez unitaria

$\alpha (t) = (\cos (t), \sin (t))$

${\alpha}’ (t) = ( – \sin (t) , \cos (t))$

$\big\| {\alpha}’ (t) \big\| = 1$

Circunferencia de radio $2$ parametrizada con rapidez unitaria

$\alpha (t) = 2 \big( \cos (t), \sin (t) \big)$

${\alpha}’ (t) = 2 \big( – \sin (t) , \cos (t) \big)$

$\big\| {\alpha}’ (t) \big\| = 2$

Reparametricemos

$t = h(s)$ inyectiva, creciente, derivable.

$\beta (s) = \alpha (h(s))$

Tal que $\big\| {\beta \, }’ (s) \big\| = 1$

Como $\beta (s) = \alpha \big( h(s) \big)$ entonces, ${\beta \, }’ (s) = {\alpha}’ \big( h(s) \big) h’ (s).$

Luego, $ \big\| {\alpha}’ (h(s)) \big\| h’ (s) = 1 $

$2 h’ (s) = 1$

$h’ (s) = \frac{1}{2}$

Entonces, nos sirve la función $h(s) = \frac{1}{2}s $

$\beta (s) = 2 \big(\cos \big(\frac{1}{2} s \big), \sin \big(\frac{1}{2} s \big) \big)$

${\beta \, }’ (s) = 2 \big( – \frac{1}{2} \sin \big(\frac{1}{2} s \big), \frac{1}{2} \cos \big(\frac{1}{2} s \big) \big)$

${\beta \, }’ (s) = \big( – \sin \big(\frac{1}{2} s \big), \cos \big(\frac{1}{2} s \big) \big)$

$\big\| {\beta \, }’ (s) \big\| = 1$

${\beta}^{\prime \prime} (s) = 2 \big( – \frac{1}{2} \cos \big(\frac{1}{2} s \big), – \frac{1}{2} \sin \big(\frac{1}{2} s \big) \big)$

$\big\| {\beta}^{\prime \prime} (s) \big\| = \frac{1}{2}$

Circunferencia de radio $r > 0$

$\alpha (s) = r \big(\cos \big(\frac{1}{r}s \big), r \sin \big(\frac{1}{r}s \big) \big)$

${\alpha}’ (s) = \big(- \sin \big(\frac{1}{r}s \big), \cos \big(\frac{1}{r}s \big) \big)$

${\alpha}^{\prime \prime} (s) = \big( – \frac{1}{r} \cos \big(\frac{1}{r}s \big), – \frac{1}{r} \sin \big(\frac{1}{r}s \big) \big)$

$\big\| {\alpha}^{\prime \prime} (s) \big\| = \frac{1}{r}$ es la «curvatura».

En general, dada una curva $\alpha : I \subset \mathbb{R} \rightarrow \mathbb{R}^n$ si ${\alpha \, }’ (t_0) \neq \vec{0}$, podemos definir «el» vector tangente unitario como $$\textcolor{ForestGreen}{\vec{T} (t_0) = \frac{{\alpha \, }’ (t_0) }{ \big\| {\alpha \, }’ (t_0) \big\|}}$$

Si la curva está parametrizada con rapidez unitaria $\alpha (s) $ tal que existe ${\alpha}’ (s)$ con $\big\|{\alpha \, }'(s) \big\| = 1$ para toda $s$, se tiene que $$T(s) = {\alpha \, }’ (s)$$

Dada una curva $\alpha (t)$, de clase $\mathcal{C}^1$, podemos reparametrizarla con rapidez unitaria.

Si ${\alpha \, }’ (t) \neq \vec{0} \; \; \forall \, t$; decimos que la curva es «regular».

Buscamos una función $t = h(s)$ tal que $\beta = \alpha \circ h$ y ${\beta \, }’ (s) = {\alpha \, }’ (h(s)) h’ (s)$ y que cumple que $\big\| {\beta \, }’ (s) \big\| = 1$ entonces $\big\|{\beta\, }’ (s) \big\| = \big\|{\alpha \, }’ (h(s)) \big\| h’ (s)$, con $h$ una función creciente.

Por lo que $$h’ (s) = \frac{1}{ \big\|{\alpha \, }’ (h(s)) \big\|}$$

Si además podemos que ${\alpha}^{\prime \prime} (s) \neq \vec{0}$ entonces, definimos «el» vector normal $N (s)$ como $$\textcolor{NavyBlue}{N (s) = \frac{{\alpha}^{\prime \prime} (s)}{\big\|{\alpha}^{\prime \prime} (s) \big\|}}$$

Dada una curva $\alpha (t)$, si ${\alpha \, }’ (t) \neq 0$ y existe ${\alpha}^{\prime \prime} (t)$ entonces $${\alpha}^{\prime \prime} (t) = \lambda {\alpha \, }’ (t) + \beta (t) $$

donde ${\alpha}^{\prime \prime} (t)$ es la aceleración,

${\alpha \, }’ (t)$ es la aceleración tangencial, y

$\beta (t)$ es la aceleración normal.

Es decir $${\alpha}^{\prime \prime} (t) = \lambda T (t) + N (t) $$

¿Cuál es la circunferencia osculatriz?

El radio está dado por $$\textcolor{BrickRed}{\frac{1}{\big\|{\alpha}^{\prime \prime} (s_0) \big\|}}$$

El centro de la circunferencia osculatriz es $$\alpha (s_0) + \frac{1}{\big\|{{\alpha \, }’ \, }’ (s_0) \big\|}.N(s_0) $$ $$\alpha (s_0) + \frac{1}{\|{\alpha}^{\prime \prime} (s_0) \big\|}. \frac{{\alpha}^{\prime \prime} (s_0)}{ \big\|{\alpha}^{\prime \prime} (s_0) \big\|}$$ $$ \textcolor{BrickRed}{\text{Centro} = \alpha (s_0) + \frac{{\alpha }^{\prime \prime} (s_0)}{{\big\|{\alpha}^{\prime \prime} (s_0)} \big\|^2}}$$

En conclusión, la curvatura mide el cambio en la dirección comparado con el cambio en la longitud de arco recorrida.

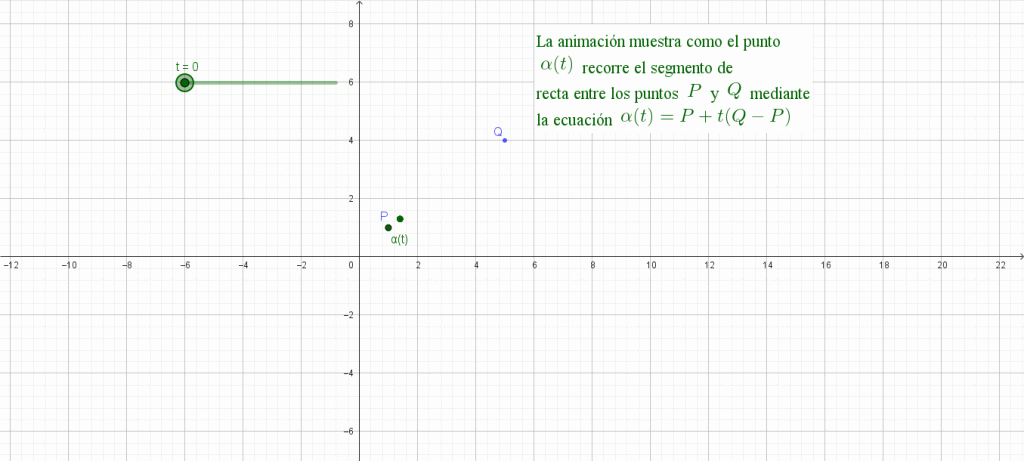
En la siguiente imagen puedes observar una animación de lo explicado en esta entrada.

https://www.geogebra.org/classic/atjan5cd

Demostración:

Primer inciso:

Por hipótesis, $f, g:\mathbb{R}^n \longrightarrow \mathbb{R}$ continuas.

(1) $\big[$ por demostrar: $ f + g : A \subseteq \mathbb{R}^n \rightarrow \mathbb{R}$ es continua.$\big]$

Sea $x_0 \in A.$

Sea $\epsilon > 0.$

Como $f$ es continua, existe $\delta_1 > 0 $ tal que si $x \in B_{\delta_1}(x_0) $ entonces $ f(x) \in B_{\frac{\epsilon}{2}}(f(x_0))…….(1)$

También, como $g$ es continua, existe $\delta_2 > 0 $ tal que si $x \in B_{\delta_2}(x_0) $ entonces $ g(x) \in B_{\frac{\epsilon}{2}} \big( g(x_0) \big)…….(2)$

Luego, si $x \in B_{\delta_3}(x_0) \Rightarrow f(x) + g(x) \in B_{\epsilon} \big( f(x_0) + g(x_0) \big)$ con $\delta_3 = mín \big\{ \delta_1 , \delta_2 \big\}$ ya que de $(1)$ y $(2)$:

Sumando $ \big\| f(x) \, – \, f(x_0) \big\| < \frac{\epsilon}{2}$ y $\big\| g(x) \, – \, g(x_0) \big\| < \frac{\epsilon}{2}$ se tiene que $$\big\| f(x) \, – \, f(x_0) \, + \, g(x) \, – \, g(x_0) \big\| \leq \big\| f(x) \, – \, f(x_0) \big\| + \big\| g(x) \, – \, g(x_0) \big\| < \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon $$

Segundo inciso.

Por hipótesis, $f, g:\mathbb{R}^n \longrightarrow \mathbb{R}$ continuas.

(2) $\big[$ por demostrar: $f . g : A \subseteq \mathbb{R}^n \rightarrow \mathbb{R}$ es continua.$\big]$

Sea $x_0 \in A.$

Sea $\epsilon > 0.$

Sea $\delta_0$ tal que si $x \in B_{\delta_0}(x_0)$ entonces $ \big| f(x) \big| < 1 + \big| f(x_0) \big|$

Como $f$ es continua, existe $\delta_1 > 0 $ tal que si $x \in B_{\delta_1}(x_0) $ entonces $ f(x) \in B_{\frac{\epsilon}{2}} \big( f(x_0) \big)…….(1)$

También, como $g$ es continua, existe $\delta_2 > 0 $ tal que si $x \in B_{\delta_2}(x_0) $ entonces $ g(x) \in B_{\frac{\epsilon}{2}} \big( g(x_0)\big)…….(2)$

Luego, si $x \in B_{\delta_3}(x_0)$ entonces $f(x).g(x) \in B_{\epsilon} \big( f(x_0).g(x_0) \big).$

Sea $ \delta_3 = mín \big\{ \delta_0 , \delta_1 , \delta_2 \big\}$

$\big[$ por demostrar: $ \big|f(x)g(x) \, – \, f(x_0)g(x_0) \big| < \epsilon.$ $\big]$

$\begin{align*} \big| f(x)g(x) \, – \, f(x_0)g(x_0) \big| &= \big| f(x)g(x) \, – \, f(x)g(x_0) \, + \, f(x)g(x_0) \, – \, f(x_0)g(x_0) \big| < \big| f(x)g(x) \, – \, f(x)g(x_0) \big| + \big| f(x)g(x_0) \, – \, f(x_0)g(x_0) \big| \\ \\ &= \big| f(x)|.|g(x) \, – \, g(x_0) \big| + \big| f(x) \, – \, f(x_0) \big|.\big| g(x_0) \big| \leq \big|(1 + \big| f(x_0) \big| \big) \big| g(x) \, – \, g(x_0) \big| + \big| f(x) \, – \, f(x_0) \big|. \big| g(x_0) \big| \\ \\ &\leq \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon \end{align*}$

Sea $f : \mathbb{R}^2 \longrightarrow \mathbb{R}$

$$f(x, y) = \left\{ \begin{array}{rcl} \frac{y}{x} & si & x \neq 0 \\ 0 & si & x = 0\end{array} \right.$$

Queremos saber:

• ¿En qué puntos $f$ tiene límite?
• ¿En qué puntos $f$ no tiene límite?
• ¿Cómo es la gráfica de $f$ ?

Analicemos diferentes cortes para poder responder estas preguntas.

1. Cortes paralelos al plano $yz$

$x = x_0$ constante.

$$f(x_0, y) = \left\{ \begin{array}{rcl} \frac{y}{x_0} & si & x_0 \neq 0 \\ 0 & si & x_0 = 0\end{array} \right.$$

Corte especial para $x = 0$

para $x = x_0 = 0$

$$f(0, y) = 0$$

En la siguiente animación, puedes ver los cortes para diferentes valores de $x_0$.

https://www.geogebra.org/classic/vaquauek

2. Cortes con el plano $x=1$

$z=f(1, y) = \frac{y}{1}$

https://www.geogebra.org/classic/mt9rgkzj

3. Cortes paralelos al plano $xz$

$y = y_0$ constante.

$$f(x, y_0) = \left\{ \begin{array}{rcl} \frac{y_0}{x} & si & x \neq 0 \\ 0 & si & x = 0\end{array} \right.$$

Corte especial para $y=0$

para $y=y_0=0$

$f(x, 0) = 0$

$$f(x, 0) = \left\{ \begin{array}{rcl} 0 & si & x \neq 0 \\ 0 & si & x = 0\end{array} \right.$$

En la siguiente animación, puedes ver los cortes para diferentes valores de $y_0$.

https://www.geogebra.org/classic/cmppwyss