Introducción

Continuaremos nuestro estudio de la medida exterior. Estudiaremos algunos resultados importantes relacionados con la aditividad de la medida exterior. Veremos también un ejemplo clásico de que la medida exterior no es aditiva: El conjunto de Vitali.

Algunos resultados de aditividad para la medida exterior.

Proposición (subaditividad numerable ó $\sigma$-subaditividad). Si $A=\bigcup_{k=1}^{\infty} A_k$ entonces $$\lambda^*(A)\leq \sum_{k=1}^{\infty} \lambda^*(A_k).$$

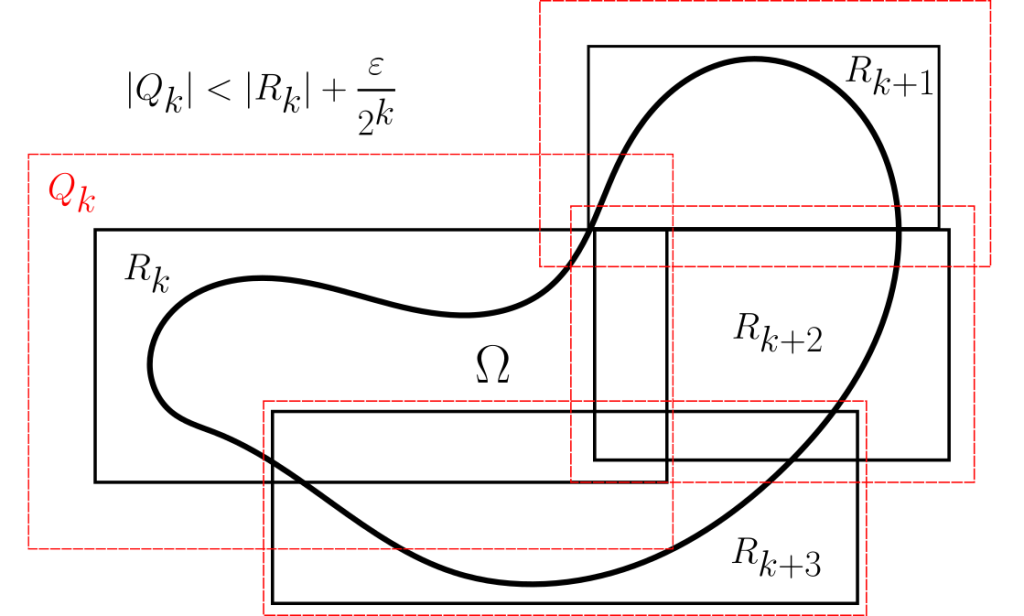
Demostración. Si alguno de los $A_k$ es de medida exterior infinita, se da la igualdad (¿Porqué?). Así que supongamos que $\lambda^*(A_k)<\infty$ para todo $k$. Sea $\varepsilon>0$ arbitrario. Por definición de medida exterior, para cada $k$, podemos encontrar una cubierta de rectángulos (digamos, cerrados) $A_k\subseteq \bigcup_{j=1}^{\infty}R_j^k$ tal que: $$\lambda^*(A_k) \leq \sum_{j=1}^{\infty} |R_j^k|\leq \lambda^*(A_k) +\frac{\varepsilon}{2^k}.$$ Luego, $A\subseteq\bigcup_{k,j\in \mathbb{N}}R_j^k$ es una cubierta de $A$ con rectángulos cerrados. De modo que:

\begin{align*} \lambda^*(A)\leq \sum_{j,k\in \mathbb{N}}|R_j^k| &= \sum_{k=1}^{\infty}\sum_{j=1}^{\infty} |R_j^k| \\
&\leq \sum_{k=1}^{\infty} \left( \lambda^*(A_k) +\frac{\varepsilon}{2^k}\right) \\ &= \sum_{k=1}^{\infty} \lambda^*(A_k) + \varepsilon.
\end{align*}

Como lo anterior es cierto para cualquier $\varepsilon>0$, concluimos que $\lambda^*(A)\leq \sum_{k=1}^{\infty} \lambda^*(A_k)$.

$\square$

La demostración del siguiente corolario es sencilla y se deja como tarea moral.

Corolario (subaditividad). Si $A=\bigcup_{k=1}^{N} A_k$ entonces $$\lambda^*(A)\leq \sum_{k=1}^{N} \lambda^*(A_k).$$

$\square$

El siguiente corolario es relevante.

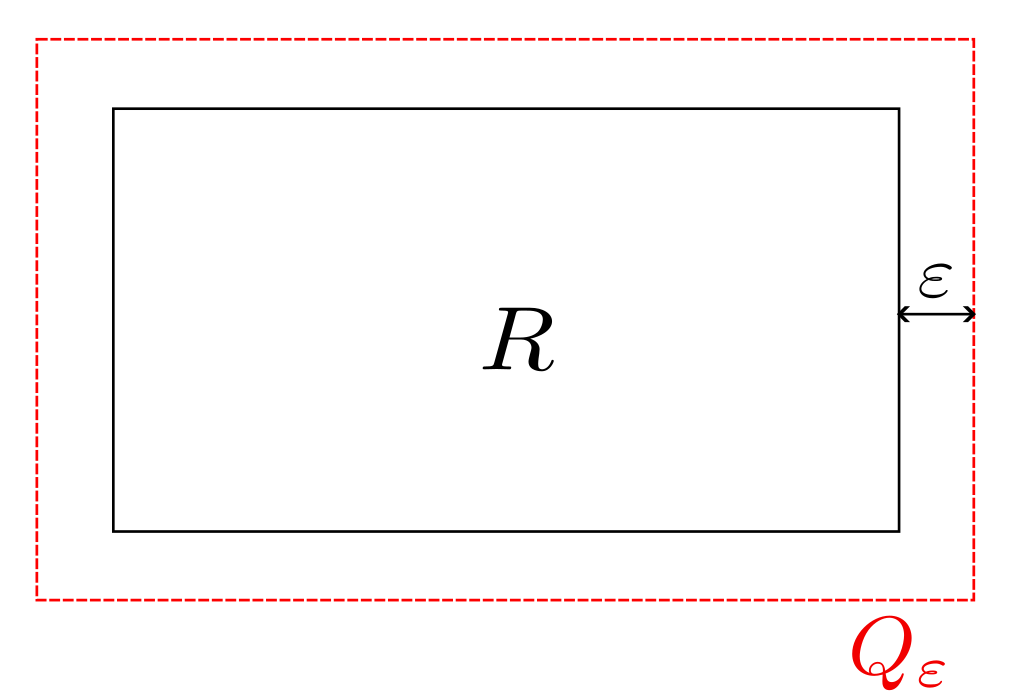
Corolario (aproximación por conjuntos abiertos). Dado $A\subseteq \mathbb{R}^n$ entonces $$\lambda^*(A)=\inf \left\{ \lambda^*(U) \ : \ A\subseteq U \text{ y } U \text{ es un conjunto abierto}\right\}.$$

Demostración. Si $\lambda^*(A)=\infty$, esto es inmediato pues $A\subseteq \mathbb{R}^n$ es abierto con $\lambda^*(\mathbb{R}^n)=\infty$ y cualquier abierto que contenga a $A$ debe tener medida exterior infinita. Así que supongamos que $\lambda^*(A)<\infty$.

Por definición de ínfimo y monotonía, es claro que: $$\lambda^*(A) \leq \inf \left\{ \lambda^*(U) \ : \ A\subseteq U \text{ y } U \text{ es un conjunto abierto}\right\}.$$

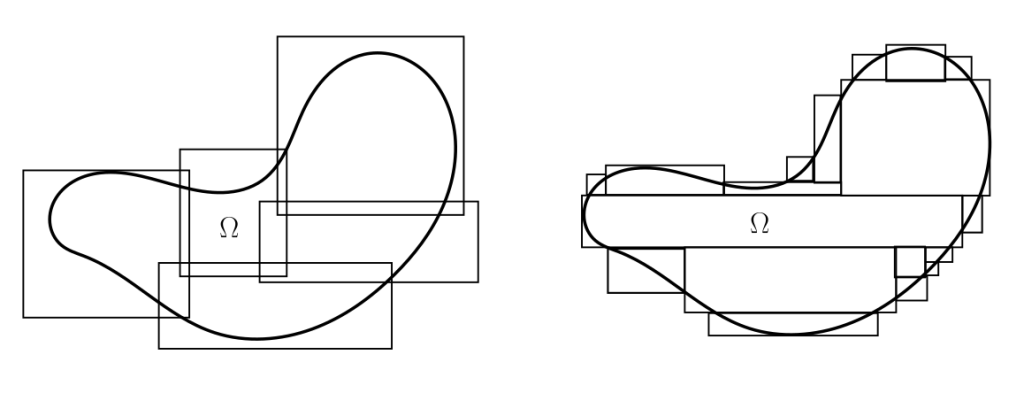
Para establecer la desigualdad opuesta, dado $\varepsilon>0$ podemos encontrar una cubierta de $A$ con rectángulos abiertos $A\subseteq \bigcup_{k=1}^{\infty} R_k$, tales que $\sum_{k=1}^{\infty} |R_k| < \lambda^*(A)+\varepsilon$. El conjunto $ \bigcup_{k=1}^{\infty} R_k$ es abierto al ser unión de abiertos. Se sigue por subaditividad: $$\lambda^*(A)\leq \lambda^*\left(\bigcup_{k=1}^{\infty} R_k\right)\leq \sum_{k=1}^{\infty}\lambda^*(R_j)=\sum_{k=1}^{\infty} |R_k|<\lambda^*(A)+\varepsilon.$$ Como lo anterior es cierto para cualquier $\varepsilon>0$, concluimos la desigualdad buscada.

$\square$

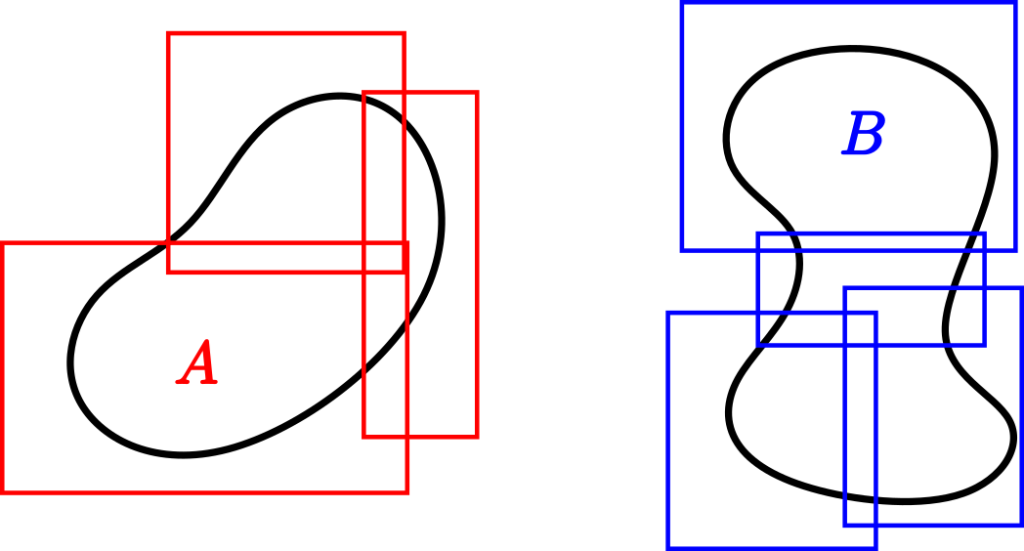
Proposición (aditividad para conjuntos separados). Si $A,B\subseteq \mathbb{R}^n$ y $d(A,B)>0$ entonces $$\lambda^*(A\cup B)=\lambda^*(A)+\lambda^*(B).$$ Donde $d(A,B)$ es la distancia entre $A$ y $B$ que se define como $d(A,B)=\inf \{d(x,y) \ | \ x\in A_1 \text{ y } x\in A_2\}$.

Demostración. Por la subaditividad, ya sabemos que $$\lambda^*(A\cup B)\leq \lambda^*(A)+\lambda^*(B).$$ Así que sólo falta establecer la desigualdad opuesta. Si $A$ ó $B$ son de medida exterior infinita, la (des)igualdad se da de manera obvia, así que podemos suponer sin pérdida de generalidad que $A$ y $B$ son de medida exterior finita (en cuyo caso $A\cup B$ también es de medida exterior finita).

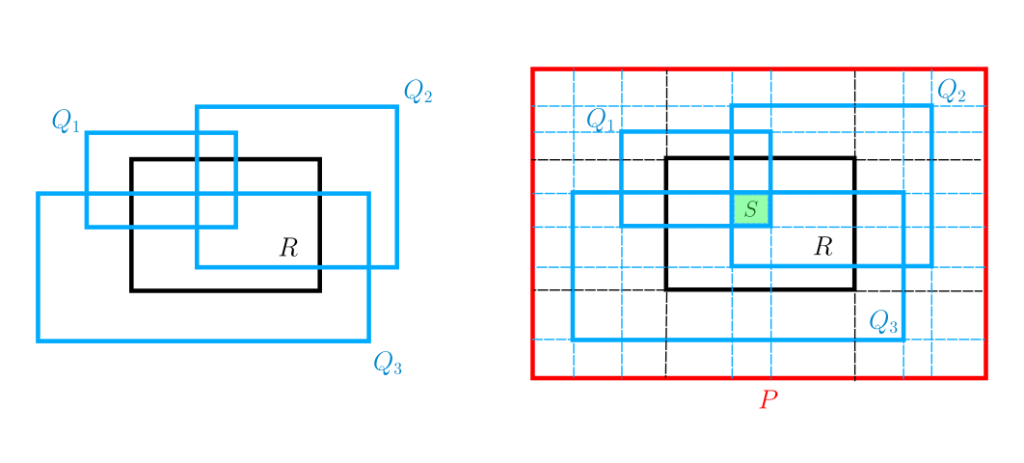
Sea $d=\frac{1}{2}d(A,B)>0$. Dado $\varepsilon>0$, podemos encontrar una cubierta de $A\cup B$ con rectángulos cerrados $A\cup B \subseteq \bigcup_{k=1}^{\infty} R_k$ tal que $\sum_{k=1}^{\infty}|R_k|<\lambda^*(A\cup B)+\varepsilon$. Más aún, podemos suponer sin pérdida de generalidad que cada $R_k$ tiene diámetro menor a $d$. (Recuerda que el diámetro de un conjunto $S$ se define como $diam(S)=\sup\{d(x,y) \ : \ x,y\in S \}$):
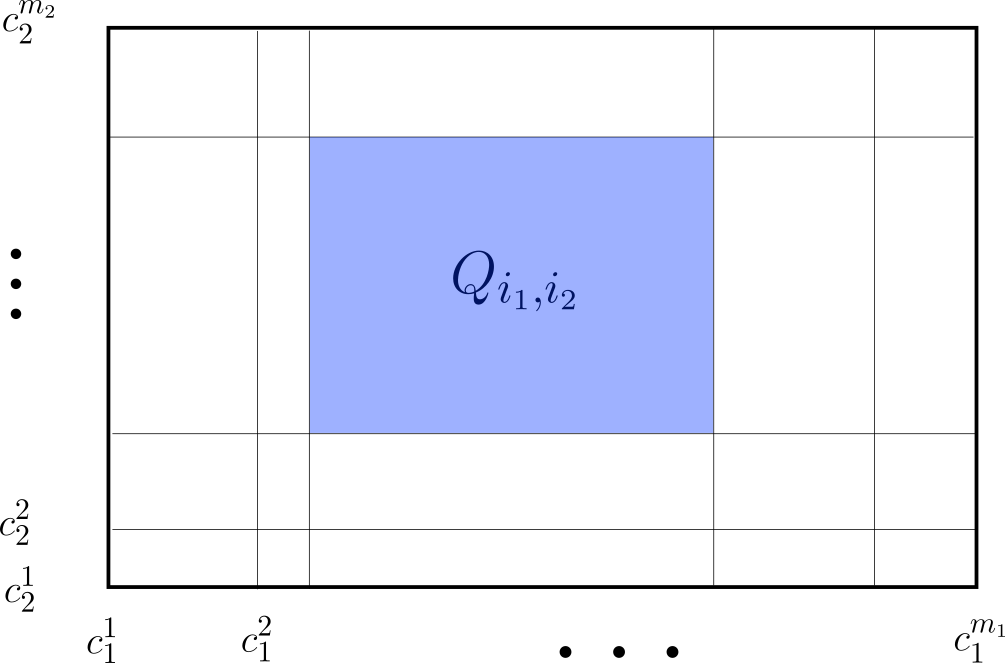
Si algún $R_k$ no cumple que $diam(S)<d$, lo subdividimos en subrectángulos más pequeños $R_k^1,\dots, R_k^{m_k}$ con $diam(R_k^j)<d$ para $j=1,\dots,m_k$. Al reemplazar $R_k$ por $R_k^1,\dots, R_k^{m_k}$ en la cubierta, se mantienen las propiedades esenciales, pues $R=\bigcup_{j=1}^{m_k}R_k^{m_k}$ y $|R|=\sum_{j=1}^{m_k}|R_k^{m_k}|$ (propiedades del volumen de rectángulos). Es decir, la nueva colección de rectángulos sigue siendo una cubierta de $A\cup B$ y la suma de los volúmenes de rectángulos se preserva.

Observa que para cada $k$, si $R_k\cap A\neq \emptyset$ entonces $R_k\cap B = \emptyset$ y si $R_k\cap B\neq \emptyset$ entonces $R_k\cap A = \emptyset$. De no ser así necesariamente existen $a\in R_k \cap A$ y $b\in R_k \cap B$, de modo que $d(A,B)\leq d(a,b)\leq \text{diam}(R_k)< d =\frac{1}{2}d(A,B)$ lo cual es absurdo.

Si denotamos por $I_A$ al conjunto de índices $k$ tales que $R_k\cap A\neq \emptyset$ y definimos análogamente $I_B$, se verifica:
$$A\subseteq \bigcup_{k\in I_A}R_k; \ \ \ \ B\subseteq \bigcup_{k\in I_B}R_k$$ De donde:

\begin{align*} \lambda^*(A)+\lambda^*(B) &\leq \sum_{k\in I_A}|R_k|+\sum_{j\in I_B }|R_j| \\ &\leq \sum_{k=1}^{\infty} |R_k| \\ &< \lambda^*(A\cup B)+\varepsilon
\end{align*}

Al ser esto cierto para cualquier $\varepsilon>0$ concluimos que $\lambda^*(A\cup B)=\lambda^*(A)+\lambda^*(B)$.

$\square$

Corolario. Si $K_1,K_2$ son compactos ajenos, entonces $\lambda^*(K_1\cup K_2)=\lambda^*(K_1)+\lambda^*(K_2)$.

$\square$

La demostración se reduce a probar que cualesquiera dos compactos ajenos tienen distancia positiva (se deja como tarea moral).

Insuficiencia de la medida exterior.

Hasta ahora la medida exterior parece un gran candidato para la definición de medida. Sin embargo, carece de una propiedad clave: la aditividad. En el siguiente ejemplo clásico veremos primero que no se satisface una propiedad más fuerte: la aditividad contable, esto es, si $A=\bigcup_{k=1}^{n}A_k$ con $A_1,A_2,\dots$ conjuntos ajenos dos a dos, entonces $\lambda^*(A)=\sum_{k=1}^{\infty} \lambda^*(A_k)$.

Ejemplo (Conjunto de Vitali). Considera la siguiente relación de equivalencia en $[0,1]$: $x\sim y$ $\iff$ $x-y\in \mathbb{Q}$. Asumiendo el axioma de elección, podemos tomar exactamente un representante de cada clase de equivalencia. Llamemos a este conjunto $$V\subseteq[0,1].$$

Para cada $q\in \mathbb{Q}$ podemos tomar la traslación de $V$ por $q$: $V+q$. Observa que si $q\neq r$ entonces $(V+q)\cap (V+r)=\emptyset$. De no ser así existiría $x=v_1+q=v_2+r\in V+q\cap V+r$ $\implies$ $(v_1-v_2)=(r-q)\in \mathbb{Q}$ $\implies$ $v_1\sim v_2$ lo cual es imposible por la definición de $V$.

Por la invarianza de la medida exterior bajo traslaciones tenemos $\lambda^*(V)=\lambda^*(V+q)$ $\forall q\in \mathbb{Q}$. Sea entonces $\{r_1, r_2\dots \}$ una numeración de los racionales en $[-1,1]$ y definamos la unión ajena: $$U=\bigcup_{k=1}^{\infty} (V+r_k) $$ Claramente $U\subseteq [-1,2]$ $\implies$ $\lambda^*(U)\leq \lambda^*([-1,2])=3$. Por otro lado veamos que $[0,1]\subseteq U$: dado $x\in[0,1]$, hay algún $v\in V$ tal que $v\sim x$, es decir $v-x=-q’\in \mathbb{Q}\cap [-1,1]$. Pero $q’=r_k$ para algún $k$, de donde $x=v+q’=v+r_k\in V+r_k \subseteq U$. Como esto es cierto para todo $x\in [0,1]$, concluimos que $[0,1]\subseteq U$.

Como $[0,1]\subseteq U \subseteq [-1,2]$ $\implies$ $1 \leq \lambda^*(U) \leq 3 $.

Por la sigma-subaditividad y la invarianza bajo traslaciones sabemos que: $1\leq \lambda^*(U)\leq\sum_{k=1}^{\infty}\lambda^*(V+r_k) = \sum_{k=1}^{\infty}\lambda^*(V)$, así que necesariamente $\lambda^*(V)>0$.

Si suponemos que la medida exterior es aditiva contable, tendríamos $$\lambda^*(U)=\lambda^*(\bigcup_{k=1}^{\infty} (V+r_k))=\sum_{k=1}^{\infty}\lambda^*(V+r_k)=\sum_{k=1}^{\infty}\lambda^*(V)=\infty$$

Pues $\lambda^*(V)>0$, esto es incompatible con nuestra estimación previa $1 \leq \lambda^*(U) \leq 3 $, lo cual es absurdo. Por tanto, la medida exterior no es contable aditiva.

De hecho tampoco puede ser aditiva: Supongamos por el contrario que la medida exterior es aditiva. Como $\lambda^*(V)>0$ existe algún natural tal que $\lambda^*(V)>\frac{1}{n}$. Ahora, si tomamos cualquier subconjunto finito $J$ de $\mathbb{Q}\cap [-1,1]$ con cardinalidad $3n$ tendríamos similarmente
$$\lambda^*(\bigcup_{q\in J} (q+V))=\sum_{q\in J} \lambda^*(q+V)=3n( \lambda^*(V))>3n\frac{1}{n}=3.$$ Lo que de nuevo contradice nuestras estimaciones previas, por tanto la medida exterior tampoco puede ser aditiva.

$\triangle$

El conjunto anterior es un ejemplo clásico de Conjunto no medible (de manera informal, son conjuntos con propiedades «patológicas» respecto a la medida exterior). Pronto veremos qué significa ser un conjunto medible y sus principales consecuencias. Es posible generalizar este contraejemplo a más dimensiones.

La aparición del axioma de elección en esta parte es un hecho bastante delicado. Asumiéndolo, es posible probar que NO EXISTE ninguna función de los subconjuntos de $\mathbb{R}^n$ a los reales positivos que satisfaga simultáneamente la monotonía, la aditividad y la normalización (de ahí la necesidad de «restringirnos» a clases de conjuntos especiales, como los conjuntos medibles que estudiaremos más adelante). Existen algunas nociones de «medida» que niegan este axioma y en las que todos los subconjuntos de $\mathbb{R}$ son medibles, aunque estas suelen presentar serias limitaciones operativas. Más sobre estos temas se pueden consultar en (Wagon, 1993) y (Solovay, 1970).

Más adelante…

Hemos encontrado una primera dificultad con la medida exterior: No es aditiva. En la siguiente entrada definiremos el concepto de conjunto medible: Los conjuntos «bien portados» bajo la medida exterior y sobre los cuales podemos definir una noción adecuada de medida.

Tarea moral

• Demuestra la subaditividad de la medida exterior: si $A=\bigcup_{k=1}^{\infty} A_k$ entonces $$\lambda^*(A)\leq \sum_{k=1}^{\infty} \lambda^*(A_k).$$
• Prueba que si $K_1$ y $K_2$ son conjuntos compactos ajenos, entonces $d(K_1,K_2)>0$.
• Sean $A\subseteq B \subseteq \mathbb{R}^n$. Demuestra que $$\lambda^*(A)\leq \lambda^*(B)+\lambda^*(B\setminus A).$$
• Prueba que $$\lambda^*(\mathbb{R})\leq \lambda^*(\mathbb{Q}) +\lambda^*(\mathbb{R}\setminus \mathbb{Q}).$$Usa este hecho para dar una demostración alterna de que el conjunto de números irracionales es no-numerable.
• Dados $A,B\subseteq \mathbb{R}^n$ demuestra que $$\lambda^*(A\cup B)+\lambda^*(A\cap B)\leq \lambda^*(A)+\lambda^*(B).$$ [SUGERENCIA: Observa que $A=(A\cap B)\cup (A\setminus B)$; $B=(A\cap B)\cup (B\setminus A)$ y $A\cup B =(A\cap B)\cup (A\setminus B) \cup (B\setminus A)$. Utiliza subaditividad.]

Referencias

• Solovay, Robert M. «A model of set-theory in which every set of reals is Lebesgue measurable.» Annals of Mathematics 92.1 (1970): 1-56.
• Wagon, Stan. The Banach-Tarski Paradox. Vol. 24. Cambridge University Press, 1993.

Introducción

En esta entrada continuaremos estudiando la medida exterior. Veremos maneras alternas de definir la medida exterior y algunos ejemplos importantes.

Más propiedades de la medida exterior.

Podemos tratar de definir una noción análoga de medida exterior reemplazando rectángulos cerrados por rectángulos abiertos. La siguiente proposición nos dice que de hecho coinciden. Esto simplificará considerablemente algunos cálculos más adelante. También ilustra una técnica que usaremos recurrentemente para aproximar una cantidad numerable de elementos: estimamos cada parte con un «error» $\varepsilon$ multiplicado por un término de alguna serie convergente (usualmente $\sum_{k=1}^{\infty} \frac{1}{2^{k}}=1$) de tal manera que el «error total» sea menor o igual a $\varepsilon$ por alguna constante.

Proposición (medida exterior con rectángulos abiertos). La medida exterior se puede calcular usando rectángulos abiertos. Definamos
$$\lambda_0^*(\Omega) = \inf \left\{ \sum_{i\in I} |Q_i| \ : \ \Omega\subseteq \bigcup_{i\in I}Q_i \right\}. $$ Donde $Q_1, Q_2\dots$ son rectángulos ABIERTOS e $I$ es un conjunto de índices a lo más numerable. Entónces $$ \lambda_0^*(\Omega)=\lambda^*(\Omega)$$

Demostración. Para la desigualdad $\geq$, dada una cubierta de $\Omega$ con rectángulos abiertos $\Omega \subseteq \bigcup_{k=1}^{\infty} Q_k$, entonces tomando la cerradura de los rectángulos: $$\Omega \subseteq \bigcup_{k=1}^{\infty} Q_k \subseteq \bigcup_{k=1}^{\infty} \overline{Q_k}.$$ Y
$$ \lambda^*(\Omega)\leq \sum_{k=1}^{\infty} |\overline{Q_k}| = \sum_{k=1}^{\infty} |Q_k|.$$ Tomando ínfimos sobre las cubiertas de rectángulos abiertos se sigue la desigualdad buscada.

Veamos la desigualdad opuesta $\leq$. Si $\lambda^*(\Omega)=\infty$, por lo anterior $\lambda_0^*(\Omega)\geq \lambda^*(\Omega) =\infty$, por tanto $\lambda_0^*(\Omega)=\infty$ y se da la igualdad. Así que basta suponer que $\lambda^*(\Omega)<\infty$.

Sea $\varepsilon>0$ arbitrario. Al ser $\lambda^*(\Omega)$ ínfimo (finito), podemos tomar una cubierta de rectángulos cerrados $\Omega\subseteq \bigcup_{k=1}^{\infty}R_k$ tal que $$\sum_{k=1}^{\infty} |R_k| < \lambda^*(\Omega) + \varepsilon \leq \sum_{k=1}^{\infty} |R_k| +\varepsilon.$$ Por la aproximación con rectángulos abiertos, para cada $k=1,2,\dots$, podemos encontrar un rectángulo abierto $Q_k$ tal que $R_k\subseteq Q_k$ y $|Q_k|<|R_k|+\frac{\varepsilon}{2^{k}}$. Entonces $\Omega\subseteq \bigcup_{k=1}^{\infty}R_k \subseteq \bigcup_{k=1}^{\infty}Q_k$. Luego: $$\lambda_0^*(\Omega)\leq \sum_{k=1}^{\infty} |Q_k|<\sum_{k=1}^{\infty}(|R_k|+\frac{\varepsilon}{2^{k}})< \lambda^*(\Omega) + 2 \varepsilon.$$ Como lo anterior es cierto para cualquier $\varepsilon>0$ se sigue que $\lambda^*(\Omega) \geq \lambda_0^*(\Omega)$.

$\square$

Como ya lo habíamos mencionado, la medida exterior de los rectángulos coincide con su volumen.

Proposición. La medida exterior de un rectángulo (abierto o cerrado) $R$ coincide con su volumen: $$\lambda^*(R)=|R|.$$

Demostración. Veamos primero el caso en el que $R=[a_1,b_1]\times [a_2,b_2]\times \dots \times [a_n,b_n]$ es cerrado. Al considerar la cubierta de $R$ con el propio $R$, se sigue de inmediato que $$0\leq \lambda^*(R)\leq |R|.$$

Veamos la desigualdad opuesta. El caso en el que $R$ es degenerado es trivial, así que supongamos que $R$ no es degenerado. La idea es usar la equivalencia de la medida exterior con rectángulos abiertos y la compacidad de $R$.

Sea $Q_1,Q_2,\dots$ cualquier cubierta de rectángulos abiertos de $R$. Supongamos sin pérdida de generalidad que la cubierta es numerable (si la cubierta es finita, el argumento debajo aplica de igual manera): $R\subseteq \bigcup_{k=1}^{\infty} Q_k$. Como $K$ es compacto, podemos extraer alguna subcubierta finita, digamos $$R\subseteq \bigcup_{k=1}^{N} Q_k.$$ Al ser una cubierta finita, se sigue de las propiedades del volumen de rectángulos que: $$|R|\leq \sum_{k=1}^{N}|Q_k| \leq \sum_{k=1}^{\infty}|Q_k|.$$ Como lo anterior es cierto para cualquier cubierta con rectángulos abiertos, al tomar ínfimos se sigue que $$|R|\leq \lambda_0^*(R)=\lambda^*(R).$$

Si $R$ es un rectángulo abierto, la cubierta de $R$ con el propio $R$ (o su cerradura) establecen $\lambda^*(R)\leq |R|$. Para la otra desigualdad podemos usar la aproximación por rectángulos cerrados, la monotonía de la medida exterior y el caso anterior: $$|R|=\sup_{\substack{Q\subseteq R; \ Q \text{ cdo.}}} \{|Q| \}=\sup_{\substack{Q\subseteq R; \ Q \text{ cdo.}}} \{ \lambda^*(Q) \} \leq \lambda^*(R).$$

$\square$

Ejemplo. Si $A\subseteq \mathbb{R}^n$ es acotado, entonces $\lambda^*(A)$ es finita pues podemos encontrar un rectángulo $R$ suficientemente grande tal que $A\subseteq R$ de modo que $\lambda^*(A)\leq \lambda^*(R)=|R|<\infty$.

$\triangle$

Ejemplo. La medida exterior de $\mathbb{R}^n$ es $\infty$.

Consideremos le sucesión de rectángulos anidados $R_k=[-k,k]\times [-k,k]\times \dots \times [-k,k]$ $k=1,2,\dots$. Luego $\lambda^*(R_k)=|R_k|=(2k)^n$. Como $R_k\subseteq \mathbb{R}^n$ $\forall$ k, entonces $(2k)^n\leq \lambda^*(\mathbb{R}^n)$ $\forall k$ así que necesariamente $\lambda^*(\mathbb{R}^n)=\infty$.

$\triangle$

Más adelante…

Seguiremos con nuestro estudio de la medida exterior. Nos enfocaremos en estudiar las propiedades relacionadas con la «aditividad» de la medida exterior, aunque veremos un ejemplo clásico de que ésta en general no es aditiva.

Tarea moral

• Usando que todo conjunto numerable tiene medida exterior cero, prueba que $\mathbb{R}^n$ NO es numerable.
• Demuestra que la medida exterior de un polígono especial coincide con su volumen.
• Demuestra que la medida exterior también se puede calcular mediante polígonos especiales. Es decir, $$\lambda^*(\Omega) = \inf \left\{ \sum_{i\in I} |P_i| \ : \ \Omega\subseteq \bigcup_{i\in I}P_i \right\}. $$ Donde $P_1, P_2\dots$ son polígonos especiales e $I$ es un conjunto de índices a lo más numerable.

Introducción

Como lo habíamos adelantado, ya podemos definir una primera noción de medida. La idea es tomar «la mejor aproximación» de un conjunto que podamos hacer mediante cubiertas de rectángulos cerrados.

Un primer intento de definir medida: La medida exterior.

Definición. Dado $\Omega \subseteq \mathbb{R}^n$ definimos su medida exterior en $\mathbb{R}^n$, $\lambda^*(\Omega)$ como: $$\lambda^*(\Omega):=\inf \left\{ \sum_{i\in I} |R_i| \ : \ \Omega \subseteq \bigcup_{i\in I} R_i \right\} $$ Donde $R_1,R_2,\dots$ son rectángulos e $I$ es un conjunto de índices a lo más numerable.

Observación. En la definición anterior usamos la convención de que $\lambda^*(\Omega)=\infty$ si y sólo si $\sum_{i\in I} |R_i|$ diverge ($=\infty$) para cualquier cubierta numerable de rectángulos $\{ R_i\}_{i\in I}$ (i.e. «cuando el conjunto es demasiado grande»). Esta convención es compatible con todos los cálculos debajo.

Para que la definición tenga sentido, habría que asegurar que cualquier subconjunto de $\mathbb{R}^n$ se puede cubrir con una cantidad numerable de rectángulos. Esto siempre es posible, considera, por ejemplo, la sucesión de rectángulos anidados $[-k,k]^n$ para $k=1,2,\dots$.

Es fácil convencerse de la necesidad de considerar subcubiertas posiblemente infinitas en la definición. En general no es claro como se podrían aproximar «bien» subconjuntos no acotados con una cantidad finita de rectángulos; ni conjuntos «curvos» como bolas o cilindros. La restricción de que el conjunto de índices sea a lo más numereable es una tecnicalidad. No es obvio como definir una suma con una cantidad no numerable de elementos y con las formas usuales de hacerlo normalmente la suma diverge si hay una cantidad no numerable de términos positivos.

Por simplicidad, en esta entrada nos referiremos a los rectángulos cerrados simplemenete como rectángulos.

Primeras propiedades de la medida exterior.

Proposición.

1. (No-negatividad) La medida exterior de cualquier subconjunto de $\mathbb{R}^n$ es no negativa.
2. (Medida exterior del conjunto vacío) $\lambda^*(\emptyset)=0$.
3. (Monotonía) Si $A\subseteq B\subseteq \mathbb{R}^n$ entonces $\lambda^*(A)\leq \lambda^*(B)$.
4. (Invarianza bajo traslaciones) Si $A\subseteq \mathbb{R}^n$ y $x\in \mathbb{R}^N$, entonces $\lambda^*(A)=\lambda^*(x+A)$.
5. (Dilataciones) Si $A\subseteq \mathbb{R}^n$ y $c\in \mathbb{R}$, entonces $\lambda^*(cA)=|c|^n\lambda^*(A)$ (donde $cA= \{ ca \ : \ a\in A \}$).

Demostración.

1. Notemos que cualquier suma de volúmenes de rectángulos es $\geq 0$ pues el volumen de cualquier rectángulo es $\geq 0$. Por tanto, para cualquier $\Omega$, 0 es cota inferior del conjunto sobre el que tomamos ínfimo, de donde $0\leq \lambda^*(\Omega)$.
2. Por vacuidad, cualquier rectángulo degenerado o con volumen arbitrariamente pequeño funge como cubierta para el vacío, por tanto, $\lambda^*(\emptyset)\leq 0$. Por no-negatividad, $\lambda^*(\emptyset)\geq 0$. Se sigue 2.
3. Si $A\subseteq B$, cualquier cubierta de rectángulos para $B$ es una cubierta de rectángulos para $A$. Tomando ínfimos sobre todas las cubiertas posibles se sigue 3.
4. A cualquier cubierta con rectángulos de $A$: $R_1,R_2,\dots$, le podemos asociar una cubierta «trasladada» para $x+A$: $x+R_1,x+R_2,\dots$. La suma de los volúmenes de los rectángulos sobre ambas cubiertas es igual debido a la invarianza bajo traslaciones del volumen de rectángulos. Inversamente a cualquier cubierta de $x+A$: $Q_1,Q_2,\dots$ le podemos asociar la cubierta de $A$: $-x+Q_1,-x+Q_2,\dots$ la suma de los volúmenes coincide por la misma razón. Se sigue 4. pues los conjuntos sobre los que tomamos ínfimos son de hecho iguales.
5. Similarmente al inciso anterior, podemos biyectar las cubiertas de $A$ con las de $cA$: A la cubierta $R_1,R_2,\dots$ de $A$ le asociamos la cubierta $cR_1,cR_2,\dots$ de $cA$ y viceversa. Por las propiedades de dilatación del volumen de rectángulos: $$\sum_{k=1}^{\infty}|cR_k|=|c|^n\sum_{k=1}^{\infty}|R_k|.$$ Tomando ínfimos sobre el conjunto de cubiertas se sigue 5.

$\square$

De momento, hacemos la distinción entre volumen y medida exterior. Aunque es tentador pensar que $|R|=\lambda^*(R)$ si $R$ es un rectángulo cerrado (y de hecho es cierto), ¡hay que probarlo! La desigualdad $\lambda^*(R)\leq |R|$ es obvia al considerar la cubierta de $R$ con el propio $R$. Sin embargo la desigualdad opuesta requiere más trabajo. No es trivial probar que $|R|$ es cota inferior de las sumas de volumenes sobre cubiertas de rectángulos para $R$.

Algunos ejemplos básicos

En general, es bastante complicado calcular la medida exterior de un conjunto arbitrario. Sin herramientas más avanzadas, lo único que podemos hacer es dar cubiertas de rectángulos cuya suma de volumenes se aproxime cada vez más a cierto valor y probar que dicho valor es una cota inferior para cualquier tal suma.
Cuando un conjunto tiene medida exterior cero, este proceso se suele simplificar bastante pues ya sabemos a priori que 0 es una cota inferior, así que basta dar cubiertas de rectángulos tal que las sumas de volúmenes se hagan arbitrariamente pequeñas.
Veamos un par de ejemplos importantes de conjuntos con medida exterior cero (o conjuntos nulos). Próximamente, aplicaremos métodos similares para calcular la medida exterior de otros conjuntos sencillos, como rectángulos y triángulos. Las técnicas de teoría de integración facilitarán en gran medida el cálculo de la medida (exterior) de conjuntos mucho más complicados.

Ejemplo. La medida exterior de un punto $\{ x \}$ con $x\in \mathbb{R}^n$ es 0. Por no-negatividad $\lambda^*(\{ x \})\geq 0$. Como el propio $\{ x \}$ es un rectángulo de volumen 0 (degenerado), al considerar la cubierta trivial $\{ x \}$, por definición de ínfimo $\lambda^*(\{ x \} )\leq |\{ x\}|=0$.

$\triangle$

Ejemplo. La medida exterior de un hiperplano $H=\mathbb{R}^{n-1}\times\{ 0\}\subseteq \mathbb{R}^n$ es 0. Consideremos la cubierta con rectángulos degenerados $\{ R_k \}_{k=1}^{\infty}$ donde $$R_k= [-k,k]\times[-k,k]\times\dots\times [-k,k]\times \{ 0\}.$$ Es claro que $H=\bigcup_{k=1}^{\infty}R_k$ y $|R_k|=0$ para todo $k$. Así $$ 0\leq \lambda^*(H)\leq \sum_{k=1}^{\infty}|R_k|=\sum_{k=1}^{\infty}0=0.$$ De donde $\lambda^*(H)=0$.

$\triangle$

Ejemplo. La medida exterior de un conjunto numerable $S=\{x_1,x_2\dots \}$ es 0. Uno simplemente puede tomar la cubierta trivial con rectángulos degenerados $\{x_1\},\{x_2 \},\dots$ Como cada uno de estos tiene volumen 0, usando la no-negatividad y la definición de ínfimo: $$0\leq \lambda^*(S)\leq \sum_{k=1}^{\infty} |\{ x_k \}|=\sum_{k=1}^{\infty}0=0.$$ De manera alternativa (y posiblemente mas ilustrativa para lo que sigue) podemos aproximar usando solamente rectángulos no degenerados:

Sea $\varepsilon>0$ arbitrario. Para cada $k=1,2,\dots$ tomemos un rectángulo no degenerado $R_k$ tal que $x_k\in R_k$ y el volumen de $R_k$ sea $<\frac{\varepsilon}{2^{k}}$ (siempre podemos hacer esto, imitando por ejemplo el argumento en la aproximación mediante rectángulos abiertos). Consideremos la cubierta por rectángulos $S\subseteq \bigcup_{k=1}^{\infty} R_k$, luego: $$0\leq \lambda^*(S)\leq \sum_{k=1}^{\infty}|R_k|<\sum_{k=1}^{\infty} \frac{\varepsilon}{2^{k}}=\varepsilon.$$

Como lo anterior es cierto para cualquier $\varepsilon>0$ necesariamente $\lambda^*(S)=0$.

$\triangle$

El ejemplo anterior es un caso particular de un resultado más general que será útil en el futuro.

Proposición. Si $A_1,A_2,\dots$ son subconjuntos de $\mathbb{R}^n$ tales que $\lambda^*(A_k)=0$ para todo $k\in \mathbb{N}$, entonces $$\lambda^*\left( \bigcup_{k=1}^{\infty}A_k \right)=0.$$

Demostración. Fijemos $\varepsilon>0$. Como $\lambda^*(A_k)=0$, por definición de ínfimo podemos encontrar una colección de rectángulos $\{ R^k_j\}_{j=1}^{\infty}$ tales que $$A_k\subseteq \bigcup_{j=1}^{\infty} R^k_j$$ Y $$\sum_{j=1}^{\infty}|R^k_j|<\frac{\varepsilon}{2^k}.$$ Consideremos la cubierta de rectángulos $\{ R^k_j\}_{j,k\in \mathbb{N}}$. Notemos que $$\bigcup_{k=1}^{\infty}A_k\subseteq \bigcup_{k,j\in \mathbb{N}}R^k_j.$$ Por lo tanto \begin{align*} 0 &\leq \lambda^*\left( \bigcup_{k=1}^{\infty} A_k \right) \\ &\leq \sum_{j,k\in \mathbb{N}}|R^k_j| \\ &=\sum_{k=1}^{\infty}\sum_{j=1}^{\infty}|R^k_j| \\ &\leq \sum_{k=1}^{\infty} \frac{\varepsilon}{2^k} \\ &= \varepsilon.\end{align*}

Como lo anterior es cierto para cualquier $\varepsilon>0$, concluimos que $$\lambda\left( \bigcup_{k=1}^{\infty}A_k \right)=0.$$

$\square$

Más adelante…

Continuaremos estudiando la medida exterior. Veremos una definición equivalente de la medida exterior usando rectángulos abiertos. También probaremos que el volumen coincide con la medida exterior de un rectángulo.

Tarea moral

• Sea $H^k_a$ un hiperplano de la forma $H^k_a=\{ (x_1,x_2,\dots, x_k,\dots, x_n) \ | \ x_k=a\}$. Demuestra que $\lambda^*(H^k_a)=0$.
• Demuestra que si $A\subseteq B$ y $\lambda^*(B)=0$, entonces $\lambda^*(A)=0$.
• Demuestra que para cualquier rectángulo $R$, $\lambda^*(\partial R)=0$, donde $\partial R$ denota la frontera del rectángulo. [SUGERENCIA: $\partial R$ está contenida en una unión finita de hiperplanos].

Introducción

Si queremos construir una noción más general de integración, un requisito mínimo es que se debe ajustar a la idea intuitiva de que la integral (al menos en $\mathbb{R}$) es el «área bajon la curva» de una función. Es entonces natural pensar en que primero hay que definir de manera precisa y lo más general posible conceptos como longitud, área, volúmen, y sus análogos en dimensiones más altas. Ésta es precisamente la idea de medida en $\mathbb{R}^n$. Más adelante construiremos la integral de Lebesgue sobre este concepto.

Idealmente, nos gustaría asignarle a cada subconjunto $A\subseteq \mathbb{R}^n$ algún número no negativo $\lambda (A)$ (su medida en $\mathbb{R}^n$). Para que ésta noción tenga sentido, debería satisfacer ciertas propiedades «intuitivas» y a las que ya estamos acostumbrados en dimensiones bajas. Las siguientes son deseables:

• Monotonía. Si $A\subseteq B$ son subconjuntos de $\mathbb{R}^n$, entonces $\lambda(A)\leq \lambda(B)$. Pues $B$ es «más grande» que $A$.
• Aditividad. Si $A\cap B=\emptyset$ son subconjuntos ajenos, entónces $\lambda(A\cup B)=\lambda(A)+\lambda(B)$.
• Normalización. La medida de un rectángulo generalizado, es decir un producto de intervalos $\prod_{i=1}^{n}[a_i,b_i]\subseteq\mathbb{R}^n$, debería ser el producto de las longitudes de sus lados: $\prod_{i=1}^{n}(b_i-a_i)$. Ésta idea coincide con el cálculo elemental de áreas de rectángulos y volúmenes de prismas rectangulares.

Podemos usar las ideas anteriores como punto de partida para intentar definir la medida de conjuntos más generales. El camino que seguiremos es: Tomar a los rectángulos como «unidades de medida» (simulando el punto 3) y buscar la mejor forma de aproximar un conjunto «por fuera» mediante rectángulos.

Rectángulos y su volumen.

Definición. Por intervalos (acotados) nos referimos a conjuntos no vacíos de $\mathbb{R}$ de la forma $[a,b]:=\{x\in \mathbb{R} \ : \ a\leq x \leq b \}$; $[a,b):=\{x\in \mathbb{R} \ : \ a\leq x < b \}$; $(a,b]:=\{x\in \mathbb{R} \ : \ a< x \leq b \}$; $(a,b):=\{x\in \mathbb{R} \ : \ a< x < b \}$, donde $a\leq b$ son números reales. Llamaremos a los intervalos de la forma $[a,b]$ como intervalos cerrados y a los de la forma $(a,b)$ como intervalos abiertos. Definimos la longitud $|I|$ de un intervalo $I=[a,b],[a,b),(a,b],(a,b)$ como $$|I|=b-a.$$ La longitud de un intervalo puede ser 0. A los intervalos de longitud 0 (i.e. que constan de un sólo elemento) los llamaremos «degenerados«.

Para esta parte, trabajaremos casi exclusivamente con intervalos cerrados o abiertos y acotados. Por brevedad nos referiremos a estos simplemente como intervalos.

Definición. Un rectángulo cerrado (abierto) en $\mathbb{R}^n$ es un producto cartesiano $$R:=I_1\times\ I_2\times \dots \times I_n.$$ Donde $I_1,I_2,\dots, I_n$ son intervalos cerrados (abiertos). Definimos el volúmen del rectángulo $R=I_1\times\ I_2\times \dots \times I_n$ como $$|R|=\prod_{k=1}^{n}|I_k|.$$ Si alguno de los intervalos componente de un rectángulo es degenerado, diremos también que el rectángulo es «degenerado».

Observaciones.

• Para cualquier rectángulo $R$, su volumen es no negativo (posiblemente 0) y finito: $0\leq |R| < \infty$. Un rectángulo tiene volúmen 0 si y sólo si es degenerado.
• Los intervalos cerrados/abiertos son rectángulos en $\mathbb{R}$. En este caso su volumen coincide con su longitud.
• Si $R\subseteq Q$ son rectángulos, entónces $|R|\leq |Q|$. Pues la única posibilidad es que al descomponer $R$ y $Q$ como producto de intervalos, cada intervalo en la descomposición de $R$ sea un subintervalo del correspondiente a $Q$ y la monotonía es inmediata en el caso de intervalos.
• La cerradura de un rectángulo $R$ es un rectángulo cerrado $\overline{R}$. Además $|R|=|\overline{R}|$.
• Los rectángulos cerrados son subconjuntos cerrados y acotados en $\mathbb{R}^n$ (por ende compactos). Los rectángulos abiertos son subconjuntos abiertos de $\mathbb{R}^n$. La cerradura de un rectángulo abierto es un rectángulo cerrado del mismo volúmen.
• El volúmen de un rectángulo, coincide con la noción de «medida» que nos da la integral de Riemann, a saber, la medida de Jordan: $J(R)=\int \chi_R = |R|$, donde $\int$ denota la integral de Riemann sobre algún rectángulo cerrado y no degenerado que contenga a $R$ y $\chi_R$ es la función característica de $R$.

Las siguientes propiedades del volúmen de los rectángulos nos serán útiles más adelante.

Proposición. (Aproximación por rectángulos abiertos y cerrados). Si $R$ es un rectángulo cerrado, entónces $$|R|=\inf \{|Q| \ :\ R\subseteq Q \text{ y $Q$ es un rectángulo abierto} \}.$$ Similarmente Si $R$ es abierto, entónces $$|R|=\sup \{|Q| \ :\ Q\subseteq R \text{ y $Q$ es un rectángulo cerrado}\ \}.$$

Demostración. Para el caso en el que $R=[a_1,b_1]\times [a_2,b_2]\times \dots \times [a_n,b_n]$ es cerrado, de las observaciones sabemos que $|R|\leq |Q|$ para cualquier rectángulo abierto tal que $R\subseteq Q$, de donde $$|R|\leq \inf\{|Q| :\ R\subseteq Q \text{ y $Q$ es un rectángulo abierto} \} .$$

Por otro lado, al definir el rectángulo abierto $$Q_{\varepsilon}=(a_1- \varepsilon,a_1+ \varepsilon ) \times (a_2-\varepsilon,a_2+\varepsilon)\times \dots \times (a_n-\varepsilon,a_n+\varepsilon)$$

Es claro que $R\subseteq Q_{\varepsilon}$ para todo $\varepsilon>0$. Usando la definición, $|Q_{\varepsilon}|$ se puede escribir como $$\prod_{k=1}^{n}(b_k-a_k)+\varepsilon f(\varepsilon)=|R|+\varepsilon f(\varepsilon)$$ Donde $f(\varepsilon)$ es algún polinomio en $\varepsilon$. Por continuidad se sigue que $\lim_{\varepsilon \to 0^+}|Q_{\varepsilon}|=|R|$. Concluimos $$|R|\geq \inf \{|Q| \ :\ R\subseteq Q \text{ y $Q$ es un rectángulo abierto} \}.$$ El argumento para rectángulos abiertos es similar.

$\square$

Proposición (Descomposición en subrectángulos preserva volúmen). Sea $R=[a_1,b_1]\times [a_2,b_2]\times \dots \times [a_n,b_n]$ un rectángulo cerrado y no degenerado. Supongamos que para cada $i=1,2,\dots ,n$ $$a_i=c_i^1<c_i^2<\dots <c_i^{m_i}=b_i.$$ Son puntos intermedios del intervalo $[a_i,b_i]$. Esto induce una descomposición de $R$ en subrectángulos: $$Q_{i_1,i_2,\dots, i_n}=[c_1^{i_1},c_1^{i_1+1}]\times [c_2^{i_2},c_2^{i_2+1}]\times \dots \times [c_n^{i_n},c_n^{i_n+1}].$$ Con $1\leq i_1 < m_1,1\leq i_2 < m_2, \dots ,1\leq i_n < m_n $. Entonces:
$$|R|=\sum_{i_1,i_2,\dots, i_n} |Q_{i_1,i_2,\dots, i_n}|.$$

Demostración. Denotemos por $J$ a las $n$-tuplas de la forma $(i_1,i_2,\dots, i_n)$ con $1\leq i_1 < m_1,1\leq i_2 < m_2, \dots 1\leq i_n < m_n $. Si definimos $d_k^j=(c_k^{j+1}-c_k^j)$ (los lados de los subrectangulos), tenemos que $(a_k-b_k)=\sum_{j=1}^{m_{i}-1} d_k^j$. Luego, lo anterior se reduce a probar:
$$\prod_{k=1}^{n}(b_k-a_k)=\prod_{k=1}^{n}\sum_{j=1}^{m_i-1}(d_k^j)=\sum_J \prod_{k=1}^{n}(d_k^{i_k}).$$

La ultima igualdad es inmediata por distributividad. (Para convencerte de esto, piensa que para desarrollar el producto de en medio, para cada $k$ hay que escoger un término $j=i_k$, multiplicar estos términos para obtener $d_1^{i_1}d_2^{i_2}\dots d_n^{i_n}$ y luego sumar sobre todas las posibles elecciones, que es precisamente el término derecho ).

$\square$

Proposición. Si $R$ es un rectángulo cerrado cubierto por una cantidad finita $N$ de rectángulos (cerrados o abiertos) no degenerados: $R\subseteq \bigcup_{k=1}^{N} Q_k$, entonces $$|R|\leq \sum_{k=1}^{N} |Q_k|.$$

Demostración. Tomando las cerraduras de $Q_1,Q_2,\dots, Q_N$ es suficiente probarlo cuando la cubierta consta de rectángulos cerrados. Al ser una cantidad finita de rectángulos, podemos encontrar un rectángulo $P$ suficientemente grande que contenga a $R,Q_1,Q_2,\dots, Q_N$. Proyectemos los extremos de los intervalos componente de cada uno de los rectángulos $R,Q_1,Q_2,\dots, Q_N$ sobre los intervalos componente de $P$. Por construcción, esto induce descomposiciones en subrectángulos en cada uno de $P,R,Q_1,Q_2,\dots, Q_n$ (observa la figura). Denotemos todos los subrectángulos (de $P$) como $S_1,S_2,\dots, S_M$. Como $R\subseteq \bigcup_{k=1}^{N} Q_k$, cada subrectángulo $S$ de $R$ debe ser también un subrectángulo de algún $Q_k$. Luego, por la proposición anterior:
$$|R|=\sum_{S_j\subseteq R} |S_j|\leq \sum_{k=1}^{N} \sum_{S_j\subseteq Q_k} |S_j|=\sum_{k=1}^{N}|Q_k|.$$

$\square$

Proposición (Invarianza bajo traslaciones). Si $R=I_1\times I_2\times \dots \times I_n$ es un rectángulo, entonces la traslación por $v=(v_1,v_2,\dots, v_n)\in \mathbb{R}^n$, $v+R$ es un rectángulo con el mismo volumen que $R$ (Donde definimos la traslación por el vector $x\in \mathbb{R}^n$ de un conjunto $B$ como $x+B=\{x+b\ : \ b\in B \}$).

Demostración. Lo anterior se cumple para intervalos abiertos/cerrados, por ejemplo si $x\in \mathbb{R}$, $x+[a,b]=[a+x,b+x]$ y $|I|=(b-a)=((b+x)-(a-x))=|x+I|$. El otro caso es similar.

Para el caso de rectángulos, es fácil ver que $v+R=(v_1+I_1)\times (v_2+I_2)\times \dots \times (v_n+I_n)$. De donde por el caso anterior: $$|R|=\prod_{k=1}^{n}|I_k|=\prod_{k=1}^{n}|v_k+I_k|=|v+R|.$$

$\square$

Proposición (Dilataciones). Si $R=I_1\times I_2\times \dots \times I_n$ es un rectángulo, entonces la dilatación $cR$ es un rectángulo con $$|cR|=|c|^n|R|. $$ (Donde definimos la dilatación por $c\in \mathbb{R}$ de un conjunto $B$ como $cB=\{cb\ : \ b\in B \}$).

Demostración. Sin pérdida de generalidad, supongamos que $R=[a_1,b_1]\times \dots \times [a_n,b_n]$ es un rectángulo cerrado. Si $c\geq 0$, es fácil ver que $cR=[ca_1,cb_1]\times \dots \times [ca_n,cb_n]$. De modo que: $$|cR|=c(b_1-a_1)\times \dots \times c(b_n-a_n)=c^n (b_1-a_1)\times \dots \times (b_n-a_n)=c^n|R|. $$

Si $c<0$, entonces $cR=[cb_1,ca_1]\times \dots \times [cb_n,ca_n]$. Luego $$|cR|=(-c)(b_1-a_1)\times \dots \times (-c)(b_n-a_n)=|c|^n (b_1-a_1)\times \dots \times (b_n-a_n)=|c|^n|R|. $$

$\square$

Más adelante…

Definiremos nuestra primera noción de medida: La medida exterior, en la que el volúmen de rectángulos juega un papel fundamental.

Tarea moral

• Decimos que un conjunto $P\subseteq \mathbb{R}^n$ es un polígono especial si puede ser representado como una unión finita de rectángulos cerrados $R_1,R_2,\dots,R_m$: $$A=\bigcup_{k=1}^{m}R_k.$$
  • Demuestra que todo polígono especial $P$ se puede expresar como una unión finita de rectángulos cerrados y con interiores ajenos $P=\bigcup_{k=1}^{m’}Q_k$. ¿La descomposición es única?
  • Con $Q_1,Q_2,\dots,Q_{m’}$ como en el inciso anterior, definimos el volumen del polígono especial $P$ como: $$|P|=\sum_{k=1}^{m’}|Q_k|.$$ Demuestra que el volumen está bien definido, es decir, no depende de la colección de rectángulos con interiores ajenos $Q_1,Q_2,\dots,Q_{m’}$.
  • Sea $R_1,R_2,\dots, R_N$ una colección de rectángulos (no necesariamente cerrados), tales que $$P\subseteq \bigcup_{k=1}^{N}R_k.$$ Demuestra que $$|P|\leq \sum_{k=1}^{N}|R_k|.$$
  • Demuestra que si $P$ es un polígono especial, entonces $x+P$ y $cP$ son polígonos especiales para cualesquiera $x\in \mathbb{R}^n$ y $c\in \mathbb{R}$. Demuestra además que $|x+P|=|P|$ y $|cP|=|c|^n|P|$.
• Demuestra que la tercer proposición de la entrada sigue siendo cierta aún si los rectángulos son degenerados.

Introducción

Esta es la primera entrada correspondiente al curso de análisis matemático II. Para esta primera parte del curso estudiaremos la integración de Lebesgue, una noción de integral muy poderosa y sobre la que se construye gran parte del análisis matemático moderno. Veremos una forma precisa de definir conceptos como longitud, área, volumen y sus análogos en más dimensiones: La medida de Lebesgue, sobre la cual construiremos este concepto de integración. Luego, estudiaremos las principales propiedades de la integral de Lebesgue, su relación con la integral de Riemann y una serie de teoremas muy útiles para calcular y estimar integrales: Los teoremas de convergencia y el teorema de Fubini.

Motivación

En tus cursos anteriores seguramente te has encontrado con el concepto de integral de Riemann. Ésta es una herramienta computacional muy poderosa que, a grosso modo, nos ayuda a encontrar el «área bajo la curva» en una dimensión y sus análogos en dimensiones más altas. Sin embargo, tiene una serie de limitaciones que hacen deseable un concepto de integración más general. A modo de motivación, recapitulamos algunas de ellas:

La clase de funciones integrables en el sentido de Riemann es limitada.

Como ejemplo, considera la función de Dirichlet $\chi_{\mathbb{Q}}:[0,1] \to \mathbb{R}$ definida como:

\begin{equation*} \chi_{\mathbb{Q}}(x)= \begin{cases} 1 & \text{si } x \in \mathbb{Q}\\ 0 & \text{si } x \in \mathbb{R}\setminus\mathbb{Q} \end{cases} \end{equation*}

Observa que si $[a,b]\subseteq [0,1]$ con $a<b$ entonces $\inf_{x \in [a,b]} f(x)=0$ y $\sup_{x \in [a,b]} f(x)=1$, pues $[a,b]$ contiene números racionales e irracionales.

Recordemos que en el contexto de integrales de Riemann las sumas inferiores y superiores de la función $f$, sobre una partición $P=\{a=x_0 < x_1 < \dots < x_n=b \}$ se definen como:
$$L(f,P,[a,b])=\sum_{j=1}^{n}(x_j-x_{j-1})\inf_{[x_{j-1},x_j]}f$$ $$S(f,P,[a,b])=\sum_{j=1}^{n}(x_j-x_{j-1})\sup_{[x_{j-1},x_j]}f$$

Y se dice que la función es Riemman integrable si $$L(f,[a,b]):= \sup_P L(f,P,[a,b])$$ Y $$S(f,[a,b]):= \inf_P S(f,P,[a,b])$$ Coinciden. La integral de Riemann se define como el valor común: $$L(f,[a,b])=S(f,[a,b]).$$
En nuestro ejemplo, es fácil ver que $L(\chi_{\mathbb{Q}},P,[a,b])=0$, $S(\chi_{\mathbb{Q}},P,[a,b])=1$ para cualquier partición $P$, de modo que $$L(\chi_{\mathbb{Q}},[a,b])=0$$ Y $$S(\chi_{\mathbb{Q}},[a,b])=1.$$ Por lo que la función NO es Riemann integrable. Sin embargo, es natural pensar que la integral debería ser 0 pues hay «muy pocos racionales en comparación con los irracionales en $[0,1]$». El siguiente ejemplo refuerza esta intuición.

La integral de Riemann no se comporta bien bajo operaciones de límite.

Si consideramos alguna numeración de los números racionales en $\mathbb{Q}\cap [0,1]=\{ r_1,r_2, \dots\}$ y para cada $k\in \mathbb{Z^+}$ definimos $f_k:[0,1]\to\mathbb{R}$ como:

\begin{equation*} f_k(x)= \begin{cases} 1 & \text{si } x \in \{ r_1,r_2,\dots, r_k \}\\ 0 & \text{en otro caso } \end{cases} \end{equation*}

Se verifica que $f_k$ es Riemann integrable y $\int_0^1f_k(x) \mathrm{d} x=0$, pues $f$ es acotada y vale 0 salvo en una cantidad finita de puntos.

Observa que si $x$ es irracional, $f_k(x)=0$ $\forall k$; y si $x$ es racional, $x=r_N$ para algún $N$ de modo que $f_k(x)=1$ $\forall n\geq N$. Esto nos dice que $\chi_{\mathbb{Q}}$ es el límite puntual de la sucesión de funciones $f_k$ pero $\chi_{\mathbb{Q}}$ no es Riemann integrable.

En el ejemplo anterior la sucesión $f_k$ se puede modificar para hacerla continua o incluso suave. Piensa por ejemplo en sustituir las discontinuidades de salto por crestas de funciones lineales a pedazos o pulsos suaves cuya anchura se va haciendo arbitrariamente pequeña. En general, esto nos dice que la clase de funciones Riemann integrables no es cerrada bajo toma de límites (puntuales), ni siquiera si las funciones son «bien portadas».

Con nociones más fuertes de convergencia, por ejemplo convergencia uniforme (una hipótesis muy «fuerte»), se tienen mejores resultados respecto a toma de límites. El siguiente es bien conocido:

Teorema. Sea $f_k:[a,b]\to \mathbb{R}$, $k\in \mathbb{N}$, una sucesión de funciones Riemann integrables que convergen uniformemente a $f:[a,b]\to \mathbb{R}$. Entonces $f$ es Riemann integrable y además $$\lim_{k\to \infty}\int_a^b f_k(x) \ \mathrm{d}x=\int_a^b f(x) \ \mathrm{d}x.$$

$\square$

También en el contexto de toma de límites, otra pregunta relevante es ¿bajo qué condiciones la integral conmuta con un límite?, o al menos ¿se puede decir algo sobre la integral de un límite?. Estas son preguntas que surgen normalmente en áreas como ecuaciones diferenciales, análisis de Fourier o probabilidad, en la que muchos conceptos se definen precisamente como un límite (por ejemplo la derivada o las series de Fourier). El ejemplo anterior no es muy esperanzador pues puede que un límite puntual ni siquiera sea Riemann integrable. Bajo ciertas condiciones sí se puede decir algo, por ejemplo:

Teorema (de la convergencia acotada). Sea $f_k:[a,b] \to \mathbb{R}$ una sucesión de funciones Riemann integrables y acotadas tales que $\exists M\in \mathbb{R}$ tal que $|f_k(x)|\leq M$ para todo $k\in \mathbb{N}$ y $x\in [a,b]$. Si $f_k$ convergen puntualmente a $f$ y $f$ es Riemann integrable, entonces $$\lim_{k \to \infty} \int_{a}^{b} f_k(x) \ \mathrm{d} x=\int_{a}^{b} f(x) \ \mathrm{d} x.$$

$\square$

¿Habrá alguna noción de integración que sea más laxa respecto a toma de límites?¿Se podrán mejorar los resultados enunciados?

La integral de Riemann no maneja adecuadamente funciones no acotadas o dominios no acotados.

Por definición, la integral de Riemann se define para funciones acotadas sobre intervalos cerrados finitos. Para funciones no acotadas o dominios no acotados la forma clásica de abordar estos problemas es con integrales impropias. Considera los siguientes ejemplos:

Ejemplo. La función $f(x)=\frac{1}{\sqrt{x}}$ no está acotada en $[0,1]$, sin embargo podemos hablar de área bajo la curva con la integral impropia:

\begin{align*} \lim_{a\downarrow 0}\int_{a}^{1}f(x) \ \mathrm{d}x &= \lim_{a\downarrow 0}\int_{a}^{1}\frac{1}{\sqrt{x}}\mathrm{d}x \\ &= \lim_{a\downarrow 0} [2x^{\frac{1}{2}}]_{a}^{1} \\ &= \lim_{a\downarrow 0} [2-2\sqrt{a}] \\
&= 2
\end{align*}

$\triangle$

Ejemplo. Algo similar ocurre con $f(x)=\frac{1}{x^2}$ pero en el intervalo $[1,\infty)$:

\begin{align*} \lim_{N\to \infty}\int_{1}^{N}f(x) \ \mathrm{d}x &= \lim_{N\to \infty }\int_{1}^{N}\frac{1}{x^2}\mathrm{d}x \\ &= \lim_{N\to \infty} \left[-\frac{1}{x}\right]_{1}^{N} \\ &= \lim_{N\to \infty} \left[ 1-\frac{1}{N}\right] \\
&= 1
\end{align*}

$\triangle$

Integrales de este tipo suelen abundar en física y probabilidad. ¿Habrá algún modo de manejar este tipo de integrales de forma unificada?

Fue precisamente por esta clase de restricciones que a finales del siglo XIX se empezaron a buscar nociones distintas o más generales de integración. Fue precisamente Henri Lebesgue quien en 1901 publicó su famoso artículo Sur une généralisation de l’intégrale définie, en el que definía una noción de integración que generalizaba a la de Riemann y resolvía varias de las limitaciones que esta presentaba.

La teoría de integración de Lebesgue y la teoría de la medida han sido tremendamente exitosas en el análisis moderno y ha encontrado aplicaciones fundamentales en áreas como la probabilidad, las ecuaciones diferenciales, la física matemática, entre otras.

Bibliografía

El material presentado en estas notas se basa en elementos tomados de la siguiente bibliografía, todas excelentes fuentes de consulta.

• Folland, Gerald B. Real analysis: modern techniques and their applications. John Wiley & Sons, 1999.
• Jones, Frank. Lebesgue integration on Euclidean space. Jones & Bartlett Learning, 2001.
• Stein, Elias M., and Rami Shakarchi. Real analysis: measure theory, integration, and Hilbert spaces. Princeton University Press, 2009.
• Tao, Terence. Analysis II. Springer Singapore, 2016.
• Wheeden, Richard Lee, and Antoni Zygmund. Measure and integral. Vol. 26. New York: Dekker, 1977.

Más adelante…

Abordaremos el problema de la medida sobre los conjuntos más sencillos: los rectángulos. Veremos algunos resultados técnicos que utilizaremos a lo largo de la construcción de la medida de Lebesgue.