Introducción

En este sección estudiamos el espacio euclideo n-dimensional, espacio que sería la base de todo el desarrollo posterior.

Definición. Como conjunto, $\mathbb{R}^{n}$ es la colección de todas las n-adas ordenadas de números reales. Es decir $$\mathbb{R}^{n}={(x_{1},x_{2},…,x_{n})|x_{i}\in \mathbb{R},~i=1,2,…,n}$4

Notación
Denotamos a un elemento de $\mathbb{R}^{n}$ por $\overline{x}=(x_{1},x_{2},…,x_{n})$\Dados dos elementos $\overline{x},\overline{y}\in \mathbb{R}^{n}$ decimos que $\overline{x}=\overline{y}\Leftrightarrow x_{i}=y_{i}$ $\forall i=1,2,…,n$.
Frecuentemente a los elementos de $\mathbb{R}^{n}$ se les denomina vectores, y con las operaciones usuales (suma y producto por un escalar), definidas como
Definición. La suma $+:\mathbb{R}^{n}\times \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ para dos elementos $\overline{x},\overline{y}\in\mathbb{R}^{n}$ se define asi:
$$\overline{x}+\overline{y}=(x_{1},x_{2},…,x_{n})+(y_{1},y_{2},…,y_{n})=(x_{1}+y_{1},x_{2}+y_{2},…,x_{n}+y_{n})$$
El producto $\overline{x}\in\mathbb{R}^{n}$ por un escalar $a\in\mathbb{R}$ como
$$\alpha(x_{1},x_{2},…,x_{n})=(\alpha x_{1},\alpha x_{2},…,\alpha x_{n})$$
$\mathbb{R}^{n}$ es un espacio vectorial.
La base canónica de dicho espacio vectorial son los vectores:$$e_{1}=(1,0,0,…,0)$$$$e_{2}=(0,1,0,…,0)$$$$.$$$$.$$$$.$$$$e_{n}=(0,0,0,…,1)$$
ya que si $\overline{x}=(x_{1},x_{2},…,x_{n})$, se tiene que $\overline{x}=x_{1}e_{1}+x_{2}e_{2}+…+x_{n}e_{n}$

Estructura Geométrica

Para dotar de una estructura geométrica al espacio $\mathbb{R}^{n}$ (que incluya los conceptos de distancia, ángulo y ortogonalidad) debemos dotar a $\mathbb{R}^{n}$ de un producto escalar.
Definición. Sea E un espacio vectorial, un producto escalar en E es una función de $E\times E$ en $\mathbb{R}$ que a cada par de vectores $\overline{x},\overline{y}$ le asocia un número $$\langle \overline{x},\overline{y}\rangle$$ que satisface las siguientes propiedades:

(a) $\langle \overline{x},\overline{x}\rangle>0$ si $\overline{x}\neq 0$
(b) $\langle \overline{x},\overline{y}\rangle=\langle \overline{y},\overline{x}\rangle$
(c) $ \langle \lambda \overline{x},\overline{y}\rangle=\lambda\langle \overline{x},\overline{y}\rangle$
(d) $\langle \overline{x}+\overline{y},\overline{z}\rangle=\langle \overline{x}+\overline{z}\rangle+\langle \overline{y},\overline{z}\rangle$
Ejemplo. Sea $C[a,b]$ el espacio lineal de todas las funciones reales continuas continuas en el intervalo $[a,b]$. Definimos $\langle f,g\rangle$ mediante la fórmula $$\langle f,g\rangle=\int_{a}^{b}f(t)g(t)dt.$$
Vamos a probar que $\langle f,g\rangle$ define un producto escalar en $c([a,b])$
(a) Tenemos que
$$\langle f,g\rangle=\int_{a}^{b}f(t)\cdot f(t)~dt=\int_{a}^{b}f^{2}(t)~dt~\geq 0~$$
la última desigualdad la justificamos usando las propiedades de la integral $\displaystyle{f\geq 0~\Rightarrow~\int_{a}^{b}f~\geq 0~}$
(b) Tenemos que
$$\langle f,g\rangle=\int_{a}^{b}f(t)g(t)~dt=\int_{a}^{b}g(t)f(t)~dt=\langle g,f\rangle$$
(c) Tenemos que
$$\langle \lambda f,g\rangle=\int_{a}^{b}\lambda~f(t)~g(t)~dt=\lambda~\int_{a}^{b}f(t)~g(t)~dt=\lambda~\langle f,g\rangle$$
(d) Tenemos que
\begin{align*} \langle f+g,h\rangle & =\int_{a}^{b}[f(t)+g(t)]h(t)~dt \\ &=\int_{a}^{b}[f(t)h(t)+g(t)h(t)]~dt \\ &=\int_{a}^{b}f(t)h(t)~dt+\int_{a}^{b}g(t)h(t)~dt \\ &=\langle f,h\rangle+\langle g,h\rangle \end{align*}
en este caso $\langle f,g\rangle$ es un producto escalar para $C[a,b]$.$\blacksquare$

El espacio normado $\mathbb{R}^{n}$

Definición. Un producto escalar $\langle,\rangle$ en un espacio vectorial E da lugar a una noción de longitud de un vector $\overrightarrow{x}\in E$, llamada su norma, y definida como
$$|\overline{x}|=\sqrt{\langle \overline{x},\overline{x}\rangle}$$
En general, una norma en un espacio vectorial E es una aplicación $x\rightarrow |x|$ de E en $(0,+\infty)$ que satisface las siguientes propiedades:
(1) $|\overline{x}|\geq 0$ para toda $\overline{x}\in\mathbb{R}^{n}$ y $|\overline{x}|=0$ si y sólo si $\overline{x}=\overline{0}$
(2) $|\lambda \overline{x}|=\lambda |\overline{x}|$ para toda $\overline{x}\in\mathbb{R}^{n}$ y $\lambda\in \mathbb{R}$
(3) $|x+y|\leq |x|+|y|$ para cualesquiera $\overline{x},\overline{y}\in\mathbb{R}^{n}$ (Desigualdad Triangular)
Al par $(E,|.|)$ se le denomina espacio normado.
Ejemplo. Veamos que
$$|\overline{x}|=\sqrt{\langle \overline{x},\overline{x}\rangle}$$
define una norma.
Solucion.
(1) Tenemos que
$$|\overline{x}|=\sqrt{\langle \overline{x},\overline{x}\rangle}\geq 0$$
la última igualdad la justificamo así: $\langle \overline{x},\overline{x}\rangle>0~\Rightarrow~\sqrt{\langle \overline{x},\overline{x}\rangle}>0$
(2) Tenemos que
\begin{align*} |\lambda \overline{x}| &=\sqrt{\langle \lambda\overline{x},\lambda\overline{x}\rangle} \\ &=\sqrt{\lambda^{2}\langle \overline{x},\overline{x}\rangle} \\ &=|\lambda|\langle \overline{x},\overrightarrow{x}\rangle\\ &=|\lambda|~|\overline{x}| \end{align*}
(3) Para la desigualdad del triángulo necesitamos antes probar un resultado
$\fbox{Lema: Desigualdad de Caychy}$
Si E es un espacio vectorial entonces $\forall~\overline{x},\overline{y}\in E$ se cumple
$$|\langle\overline{x},\overline{y}\rangle|\leq |\overline{x}|~|\overline{y}|$$
Demostración. Supongamos que $\overline{x},\overline{y}\neq 0$ y definimos
$$\overline{u}=\frac{\overline{x}}{\|\overline{x}\|}~~\overline{v}=\frac{\overline{y}}{\|\overline{y}\|}$$
Tenemos entonces que
\begin{align*} \|\overline{u}\| & =\left\|\frac{\overline{x}}{|\overline{x}|}\right\|=\frac{\|\overline{x}\|}{\|\overline{x}\|}=1 \\ \|\overline{v}\| & =\left\|\frac{\overline{y}}{\|\overline{y}\|}\right\|=\frac{\|\overline{y}\|}{\|\overline{y}\|}=1 \end{align*}
Por tanto
\begin{align*} 0\leq \|\overline{u}-\overline{v}\|^{2} & =\langle\overline{u}-\overline{v},\overline{u}-\overline{v}\rangle \\ & =\langle\overline{u}-\overline{u}\rangle-2\langle\overline{u}-\overline{v}\rangle+\overline{v}-\overline{v} \\ & =\|\overline{u}\|^{2}-2\langle\overline{u}-\overline{v}\rangle+\|\overline{u}\|^{2} \\ & =1-2\langle\overline{u},\overline{v}\rangle+1 \\ & =2-2\langle\overline{u},\overline{v}\rangle \end{align*}
Por lo tanto
\begin{align*} 0\leq 2-2\langle\overline{u},\overline{v}\rangle&~\Rightarrow~2\langle\overline{u},\overline{v}\rangle\leq 2 \\ &~\Rightarrow~\langle\overline{u},\overline{v}\rangle\leq 1 \\ &~\Rightarrow~\left\langle\frac{\overline{x}}{|\overline{x}|},\frac{\overline{y}}{\|\overline{y}\|}\right\rangle\leq 1 \\ &~\Rightarrow~\frac{1}{\|\overline{x}\|~\|\overline{y}\|}\langle\overline{x},\overline{y}\rangle\leq 1 \\ &~\Rightarrow~\langle\overline{x},\overline{y}\rangle\leq\|\overline{x}\|~\|\overline{y}\| \end{align*}
Reemplazando $\overline{x}$ por $-\overline{x}$ se obtiene que
\begin{align*} \langle\overline{-x},\overline{y}\rangle\leq\|-\overline{x}\|~\|\overline{y}\| & ~\Rightarrow~-\langle\overline{x},\overline{y}\rangle\leq~|-1|~|\overline{x}|~|\overline{y}| \\ &~\Rightarrow~\langle\overline{x},\overline{y}\rangle\geq~-\|\overline{x}\|~\|\overline{y}\| \end{align*}
con lo que queda demostrada la desigualdad.$~\blacksquare$
Regresando ahora a la desigualdad triangular tenemos que
\begin{align*} \|\overline{x}+\overline{y}\|=\sqrt{\langle\overline{x}+\overline{y},\overline{x}+\overline{y}\rangle} & ~\Rightarrow~\|\overline{x}+\overline{y}\|^{2}=\langle\overline{x}+\overline{y},\overline{x}+\overline{y}\rangle \\ & ~\Rightarrow~\|\overline{x}+\overline{y}\|^{2}=\langle\overline{x},\overline{x}\rangle+2\langle\overline{x},\overline{y}\rangle+\langle\overline{y},\overline{y}\rangle \\ &~\Rightarrow~\|\overline{x}+\overline{y}\|^{2}=\|\overline{x}\|^{2}+2\langle\overline{x},\overline{y}\rangle+|\overline{y}|^{2} \\ & ~\Rightarrow~\|\overline{x}+\overline{y}\|^{2}\leq \|\overline{x}\|^{2}+2\|\overline{x}\|~\|\overline{y}\|+\|\overline{y}\|^{2} \\ & ~\Rightarrow~\|\overline{x}+\overline{y}\|^{2}\leq \left(\|\overline{x}\|+\|\overline{y}\|\right)^{2} \end{align*}
Y tomando raíces en ambos miembros de la desigualdad, obtenemos el resultado.$~\blacksquare$

Otras normas en $\mathbb{R}^n$

Ejemplo.

$\fbox{La Norma 1 $\|\overline{x}\|_{1}$}$
Definimos $\|\\,\|_1:\mathbb{R}^n \rightarrow \mathbb{R}$ por
$\|\,\|_1 = |x_1|+\ldots+|x_n|$ $\forall \, \bar{x} \in
\mathbb{R}^n$. Vamos a probar que $\|\,\|_1 $ es una norma en
$\mathbb{R}^n$
(a) Dado que $\forall \, x \in \mathbb{R}$ $|x|\geq
0$, se tiene $\|\,\|_1 = |x_1|+\ldots+|x_n|\geq 0$ $\forall \, \bar{x} \in\mathbb{R}^n$.
(b) Si $\alpha \in \mathbb{R}$ y $\bar{x}=(x_1,\ldots,x_n) \in
\mathbb{R}^n$, entonces
\[\begin{array}{ll}
|\alpha\bar{x}| & =|\alpha x_1|+ \ldots + |\alpha
x_n|\\
\, & =|\alpha||x_1|+ \ldots + |\alpha||x_n|\\
\, & = |\alpha|(|x_1|+ \ldots + |x_n|)\\
\, & = |\alpha||\bar{x}| \quad \forall \, \bar{x}\in\mathbb{R}^n\
\end{array}\]
(c) Si $\bar{x}=(x_1,\ldots,x_n)$ y $\bar{y}=(y_1,\ldots,y_n)$ son elementos de $\mathbb{R}^n$
\[\begin{array}{ll}
|\bar{x}+\bar{y}| & =|x_1+y_1|+ \ldots + |x_n+y_n|\\
\, & \leq|x_1|+|y_1|+ \ldots + |x_n|+|y_n|\\
\, & = |x_1|+ \ldots +|x_n|+ \ldots + |y_1|+ \ldots +|y_n|\\
\, & = |\bar{x}|_1 + |\bar{y}|_1
\end{array}\]
Si $|\bar{x}|_1=0~\Rightarrow~|x_1|+ \ldots+|x_n|=0$ y como cada $|x_i|\geq 0$ $i=1,\ldots,n$ entonces $|x_1|+ \ldots +|x_n|=0~\Rightarrow~|x_i|= 0$ $i=1,\ldots,n~~~\therefore~~~\bar{x}=0$.$~~\blacksquare$
Ejemplo.
$\fbox{La Norma infinito $\|\overline{x}\|_{\infty}$}$
Consideremos ahora la función $\|\,\|_\infty:\mathbb{R}^n \rightarrow \mathbb{R}$ dada por
$$\boxed{\|\overline{x}\|_\infty=\max{|x_1|+\ldots +|x_n|}~~\forall x\in\mathbb{R}^n}$$
Vamos a probar que la función $\|\,\|_\infty:\mathbb{R}^n \rightarrow \mathbb{R}$ es una norma en $\mathbb{R}^n$, que se denomina norma del máximo o norma cúbica.
(a) Puesto que $|x_i|\geq 0~~i=1,\ldots,n$\ entonces $$\max{|x_1|+\ldots +|x_n|}\geq0$$ es decir $$\|\bar{x}\|_\infty \geq 0$$
(b) Sea $\alpha\in\mathbb{R}$ y $\bar{x}\in\mathbb{R}^n$. Se tiene entonces
que $$\|\alpha \bar{x}\|=\max\{|\alpha x_1|,\ldots,|\alpha x_n|\}=\max\{|\alpha|| x_1|,\ldots,|\alpha||x_n|\}$$
Supongamos ahora que
$$|x_{i\alpha}|=\max \{ |x_1|, \ldots, |x_n| \}$$
$\therefore~~~|x_{i\alpha}|\geq |x_i|,~~~\forall~ i=1,\ldots,n~~~\therefore~~~|\alpha||x_{i\alpha}|\geq |\alpha||x_i|,~~\forall ~~ i=1,\ldots,n$ $\therefore$ $|\alpha x_{i\alpha}|\geq |\alpha x_i|$ $\forall~~i=1,\ldots,n$ por lo que
$$|\alpha||x_{i\alpha}|= |\alpha x_{i\alpha}|=\max\{|\alpha x_1|,\ldots,|\alpha x_n|\}=\max\{|\alpha|| x_1|,\ldots,|\alpha||x_n|\}$$
es decir $$|\alpha|\max \{ |x_1|, \ldots, |x_n| \} = \max\{|\alpha x_1|,\ldots,|\alpha x_n|\}=\max\{|\alpha|| x_1|,\ldots,|\alpha||x_n|\}$$
$\therefore~~~|\alpha|\|\bar{x}\|_{\infty}=\|\alpha \bar{x}\|_{\infty}$
(c) $\|\bar{x}+\bar{y}\|_{\infty}=\max\{|x_1+y_1|,\ldots,|x_n+y_n|\}$
Sea $$|x_{1\alpha}+y_{1\alpha}|=\max\{|x_1+y_1|,\ldots,|x_n+y_n|\}$$
como $$|x_{1\alpha}+y_{1\alpha}|\leq|x_{1\alpha}|+|y_{1\alpha}|$$
se tiene que $$\max\{|x_1+y_1|,\ldots,|x_n+y_n|\}\leq|x_{1\alpha}|+|y_{1\alpha}|$$
pero por definición de $$\max\{|x_1|+\ldots+|x_n|\}~~y~~ \max\{|y_1|+\ldots +|y_n|\}$$
también se tiene que $$|x_{1\alpha}|\leq \max\{|x_1|+\ldots
+|x_n|\}~~~y~~~|y_{1\alpha}|\leq \max\{|y_1|+\ldots+|y_n|\}$$
luego $$\max\{|x_1+y_1|,\ldots,|x_n+y_n|\} \leq \max\{|x_1|+\ldots
+|x_n|\} + \max\{|y_1|+\ldots+|y_n|\}$$
o sea $$\|\bar{x}+\bar{y}\|_{\infty} \leq\|\bar{x}\|_{\infty}+\|\bar{y}\|_{\infty}.~~\blacksquare$$
Ejemplo. Norma Euclidiana
Consideremos ahora la función $\|\,\|_\infty:\mathbb{R}^n \rightarrow \mathbb{R}$ dada por
$$|x|=\sqrt{\langle x,x\rangle}$$
Vamos a mostrar que es una norma en $\mathbb{R}^n$
(a) $\|\bar{x}\|=\sqrt{x_1^2+\ldots+x_n^2} \geq 0$ pues es la raíz positiva $\therefore$ $\|\bar{x}\|\geq 0$.
(b)

\[\begin{array}{ll}
\|\alpha\bar{x}\| & = \sqrt{(\alpha x_1)^2+\ldots+(\alpha
x_n)^2}\\
\, & = \sqrt{\alpha^2x_1^2+\ldots+\alpha^2x_n^2}\\
\, & = \sqrt{\alpha^2(x_1^2+\ldots+x_n^2)}\\
\, & = \sqrt{\alpha^2}\sqrt{x_1^2+\ldots+x_n^2}\\
\, & = |\alpha|\|\bar{x}\|
\end{array}\]
(c)

\[\begin{array}{ll}
\|\bar{x}+\bar{y}\|^2 & =
(x_1+y_1)^2 + \ldots +
(x_n+y_n)^2\\
\, & =x_1^2+2x_1y_1+y_1^2 +
\ldots +
x_n^2+2x_ny_n+y_n^2\\
\, & =x_1^2+\ldots+ x_n^2 +2(x_1y_1+\ldots +x_ny_n )+ y_1^2
+ \ldots +y_n^2\\
\, & = \|\bar{x}\|^2+2(x_1y_1+\ldots +x_ny_n
)+ \|\bar{y}\|^2
\end{array}\]
Aplicando la desigualdad de Cauchy-Shwarz
$$x_1y_1+\ldots+x_ny_n \leq \|\bar{x}\|~\|\bar{y}\|$$
se tiene que $$\|\bar{x}\|^2+2(x_1y_1+\ldots+x_ny_n)+\|\bar{y}\|^2
\leq \|\bar{x}\|^2+2~\|\bar{x}\|~\|\bar{y}\|+ \|\bar{y}\|^2 =\left [\|\bar{x}\|+\|\bar{y}\|\right]^2$$
$\therefore~~~\|\bar{x}+\bar{y}\|^2\leq
\left[\|\bar{x}\|+\|\bar{y}\|\right]^2$ y al
sacar raiz obtenemos $\|\bar{x}+\bar{y}\|\leq
\|\bar{x}\|+\|\bar{y}\|$
(d) Si $\|\bar{x}\|=0$ se tiene entonces $\sqrt{x_1^2+\ldots+x_n^2}=0$ es decir $x_1^2+\ldots+x_n^2=0$ pero $x^2\geq 0~~\therefore~~x_i^2=0~~\forall~ i=1,\ldots,n$ $\therefore~~\bar{x}=0$ $\blacksquare$
El concepto general de Norma en $\mathbb{R}^n$. Las propiedades de la norma euclidiana nos ayudan para definir la noción abstracta de Norma.
Definición.Una norma en $\mathbb{R}^n$ es cualquier función $\|\,\|:\mathbb{R}^n \rightarrow
\mathbb{R}$ que satisface las siguientes propiedades que denominaremos Axiomas de Norma para cualesquiera $\bar{x},\bar{y}\,\in\,\mathbb{R}^n$ y toda $\alpha\,\in\,\mathbb{R}$ se cumple:
(a) $\|\bar{x}\|\geq 0~~\|0\|=0$
(b) $\|\alpha\bar{x}\|=|\alpha|~\|\bar{x}\|$
(c) $\|\bar{x}+\bar{y}\|\leq \|\bar{x}\|+\|\bar{y}\|$
(d) $\|\bar{x}\|=0~~\Rightarrow~\bar{x}=0$
Proposición.
Para toda norma $|\,|:\mathbb{R}^n \rightarrow\mathbb{R}$ se cumple:
(a) $\|-\bar{x}\|=\|\bar{x}\|~~\forall \, x \in \mathbb{R}^n$
(b) $|\|\bar{x}\|-\|\bar{y}\||\leq \|\bar{x}-\bar{y}\|~~\forall \, \bar{x},\bar{y} \in \mathbb{R}^n$
Proposición.
(a) $\|-\bar{x}\|=|-1|~\|\bar{x}\|=\|\bar{x}\|$
(b) $0\leq \|\bar{x}\|=\|\bar{x}-\bar{y}+\bar{y}\|\leq\|\bar{x}-\bar{y}\|+\|\bar{y}\|$
$\therefore$ $\|\bar{x}\|-\|\bar{y}\|\leq\|\bar{x}-\bar{y}\|$ Intercambiando $\bar{x}$ por $\bar{y}$ obtenemos $\|\bar{y}\|-\|\bar{x}\|\leq\|\bar{y}-\bar{x}\|=\|\bar{x}-\bar{y}\|$ $\therefore$ $|\|\bar{y}\|-\|\bar{x}\||\leq \|\bar{x}-\bar{y}\|.~~\blacksquare$

Ejemplo. Sea $I=[0,1]$. Demsotrar que $\|f\|=\sup {|f(x)|}$. Es una norma
de $C[0,1]$
Solución.
(a) Recordar que toda función real continua definida en un intervalo cerrado es acotada, por tanto $\|f\|$ está bien definida.
(b) Puesto que $|f(x)|\geq 0~\forall~x\in I$ entonces $\|f\|\geq 0$ y además, $\|f\|= 0$ sii $|f(x)|= 0~\forall~x\in I$, i.e. sii $f=0$.
(c) Recordemos un resultado: Sean $a$ y $b$ números reales tales que $a\leq b+\varepsilon$.
Demostrar que $a \leq b$
Supongase que $a>b$ entonces $a=b+\delta,~~\delta >0$ tomamos $$\displaystyle\frac{\delta}{2}=\varepsilon$$
entonces $$a > b+\delta > b +\displaystyle\frac{\delta}{2}=b+\varepsilon~ \underset{\circ}{\bigtriangledown}$$
$\therefore~a\leq b$ ahora sea $\varepsilon > 0$. Entonces existe $x_0\in I$ tal que
\[\begin{array}{ll}
|f+g|& = \sup{|f(x)+g(x)|}\\
\, & \leq |f(x_0)+g(x_0)|+\varepsilon\\
\, & \leq |f(x_0)|+|g(x_0)|+\varepsilon\\
\, & \leq \sup{|f(x)|} +\sup{|g(x)|}+\varepsilon\\
\, & = |f|+|g| +\varepsilon
\end{array}\]
$\therefore~~\|f+g\| \leq \|f\|+\|g\|$
(d) Sea $k\in \mathbb{R}$ entonces
\[\begin{array}{ll}
\|kf\| & = \sup{|kf(x)|}\\
\, & = \sup{|k||f(x)|}\\
\, & = |k|\sup{|f(x)|}\\
\, & = |k|\|f(x)\|.~~\blacksquare\\
\end{array}\]
Ejemplo. Demostrar que $\|f\|=\displaystyle\int_0^1|f(x)|dx$ es una norma de $C[0,1]$ (funciones continuas en el intervalo $[0,1]$).
Solución
(a) $\|f\|=\displaystyle\int_0^1|f(x)|dx\geq 0$ puesto que $$|f(x)|\geq 0\Rightarrow \displaystyle\int_0^1|f(x)|dx \geq 0$$
(b) Tenemos que
\[\begin{array}{ll}
\|kf\|& =\displaystyle\int_0^1|kf(x)|dx\\
\, & =\displaystyle\int_0^1|k||f(x)|dx\\
\, & =|k|\displaystyle\int_0^1|f(x)|dx\\
\, & = |k|\|f\|
\end{array}\]
(c) Tenemos que
\[\begin{array}{ll}
\|f+g\|& =\displaystyle\int_0^1|f(x)+g(x)|dx\\
\, & \leq \displaystyle\int_0^1[|f(x)|+|g(x)|]dx\\
\, & =\displaystyle\int_0^1|f(x)|dx + \displaystyle\int_0^1|g(x)|dx\
\, & = \|f\|+ \|g\|.~~\blacksquare
\end{array}\]
Ejemplo.
Definición. Sea $\|\,\|_{p}:\mathbb{R}^n \rightarrow \mathbb{R}$ dada asi: $$\|x\|_{p}=\left(\sum_{i=1}^{n}|x_{i}|^{p}\right)^{\frac{1}{p}}$$
Vamos a demostrar que $|x|_{p}$ es una norma
Solución.
(a) Puesto que $|x_i|\geq 0,~~i=1,\ldots,n$ entonces $$\sum_{1}^{n}|x_i|^{p} \geq 0~~ \therefore \left( \sum_{1}^{n}|x_i|^{p}\right)^{\frac{1}{p}}\geq 0~~ \therefore \|x\|_{p}\geq 0$$
(b) Sea $\alpha\in\mathbb{R}$ y $\bar{x}\in\mathbb{R}^n$. Se tiene entonces
que $$\|\alpha \bar{x}\|_{p}=\left(\sum_{1}^{n}|\alpha x_i|^{p}\right)^{\frac{1}{p}}=\left(|\alpha|^{p}\sum_{1}^{n}| x_i|^{p}\right)^{\frac{1}{p}}=|\alpha|\left(\sum_{1}^{n}| x_i|^{p}\right)^{\frac{1}{p}}=|\alpha|~\|x\|_{p}$$
(c) Tenemos que $$\|\overline{x}\|_{p}=\left[|x_{1}|^{p}+…+|x_{n}|^{p}\right]^{\frac{1}{p}}$$ Ahora procederemos a demostrar que cumple con la propiedad de la desigualdad del triángulo, es decir que para $\overline{x},\overline{y}\in \mathbb{R}^{n}$ $$\|\overline{x}+\overline{y}\|_{p}\leq \|\overline{x}\|_{p}+\|\overline{y}\|_{p}$$ Para ello primero procederemos a demostrar lo siguiente
Proposición. Sean p,q números reales tales que $p,q>1$ y $\displaystyle{\frac{1}{p}+\frac{1}{q}=1}$ entonces $$|ab|\leq \frac{|a|^{p}}{p}+\frac{|b|^{q}}{q}$$
Demostración. Consideremos la función $\varphi:[0,\infty)\rightarrow
\mathbb{R}$ dada por $\varphi(t)=t^{m}-mt$ con $m=\frac{1}{p}$
se tiene que $\varphi^{\prime}(t)=mt^{m-1}-m=m\left(t^{m-1}-1\right)$ por lo
que $\varphi^{\prime}(t)=0\Leftrightarrow m\left(t^{m-1}-1\right)=0\Leftrightarrow
t=1$ por lo tanto $t=1$ es un punto crítico de la función, ahora volvemos a derivar $\varphi^{\prime\prime}(t)=m(m-1)t^{m-2}$ que en $t=1$ es $<0$ por lo tanto en $t=1$, $\varphi$ alcanza un punto máximo $\therefore$ $\varphi(t)\leq \varphi(1)\Rightarrow t^{m}-mt\leq mt-m\Rightarrow t^{m}-1\leq m(t-1)$ Ahora hacemos $\displaystyle{t=\frac{|a|^{p}}{|b|^{q}}}$ y sustituimos
$$\displaystyle{\left(\frac{|a|^{p}}{|b|^{q}}\right)^{\frac{1}{p}}-1\leq
\frac{1}{p}\left(\frac{|a|^{p}}{|b|^{q}}-1\right)}$$
multiplicando ambos miembros de la desigualdad por $|b|^{q}$ se
tiene que $$\left(|b|^{q}\right)\left(\left(\frac{|a|^{p}}{|b|^{q}}\right)^{\frac{1}{p}}-1\right)\leq
\left(|b|^{q}\right)\left(\frac{1}{p}\left(\frac{|a|^{p}}{|b|^{q}}-1\right)\right)$$ lo que nos queda $$|a||b|^{q-\frac{q}{p}}-|b|^{q}\leq \frac{|a|^{p}}{p}-|b|^{q}\Rightarrow |a||b|^{q-\frac{q}{p}}\leq \frac{|a|^{p}}{p}-\frac{|b|^{q}}{p}+|b|^{q}$$
como $\displaystyle{q-\frac{q}{p}=1}$ y $\displaystyle{-\frac{|b|^{q}}{p}+|b|^{q}=\frac{|b|^{q}}{q}}$ tenemos entonces
$$|ab|\leq \frac{|a|^{p}}{p}+\frac{|b|^{q}}{q}.~~\square$$
Probaremos la desigualdad de Holder
$$\boxed{\sum_{k=1}^{n}|a_{k}b_{k}|\leq \left[\sum_{k=1}^{n}|a_{k}|^{p}\right]^{\frac{1}{p}}\left[\sum_{k=1}^{n}|b_{k}|^{q}\right]^{\frac{1}{q}}}$$
Demostración. Sea $\displaystyle{A=\left(\sum_{k=1}^{n}|a_{k}|^{p}\right)^{\frac{1}{p}}}$ y $\displaystyle{B=\left(\sum_{k=1}^{n}|b_{k}|^{q}\right)^{\frac{1}{q}}}$ y
definimos $\displaystyle{a^{\prime}_{k}=\frac{a_{k}}{A}}$ y $\displaystyle{b^{\prime}_{k}=\frac{b_{k}}{B}}$ usando la desigualdad probada anteriormente se tiene
\begin{align*}|a^{\prime}_{k}~b^{\prime}_{k}|&\leq \frac{|a^{\prime}_{k}|^{p}}{p}+\frac{|b^{\prime}_{k}|^{q}}{q}\\&\Rightarrow \sum_{k=1}^{n}|a^{\prime}_{k}b^{\prime}_{k}|\leq \sum_{k=1}^{n}\frac{|a^{\prime}_{k}|^{p}}{p}+\frac{|b^{\prime}_{k}|^{q}}{q}\\&=\sum_{k=1}^{n}\frac{|a^{\prime}_{k}|^{p}}{p}+\sum_{k=1}^{n}\frac{|b^{\prime}_{k}|^{q}}{q}\\&=\frac{1}{p}\sum_{k=1}^{n}|a^{\prime}_{k}|^{p}+\frac{1}{q}\sum_{k=1}^{n}|b^{\prime}_{k}|^{q}\\&=\frac{1}{p}\sum_{k=1}^{n}\left[\frac{a_{k}}{A}\right]^{p}+\frac{1}{q}\sum_{k=1}^{n}\left[\frac{b_{k}}{B}\right]^{q}\\&=\frac{1}{p}\frac{1}{A^{p}}\sum_{k=1}^{n}|a_{k}|^{p}+\frac{1}{q}\frac{1}{B^{q}}\sum_{k=1}^{n}|b_{k}|^{q}\end{align*}
como $$A^{p}=\left(\left(\sum_{k=1}^{n}|a_{k}|^{p}\right)^{\frac{1}{p}}\right)^{p}=\left(\sum_{k=1}^{n}|a_{k}|^{p}\right)~~~y~~~
B^{q}=\left(\left(\sum_{k=1}^{n}|b_{k}|^{q}\right)^{\frac{1}{q}}\right)^{q}=\left(\sum_{k=1}^{n}|b_{k}|^{q}\right)$$
se tiene que
\begin{align*}\frac{1}{p}\frac{1}{A^{p}}\sum_{k=1}^{n}|a_{k}|^{p}+\frac{1}{q}\frac{1}{B^{q}}\sum_{k=1}^{n}|b_{k}|^{q}&=\frac{1}{p}\frac{1} {\left(\sum_{k=1}^{n}|a_{k}|^{p}\right)}\sum_{k=1}^{n}|a_{k}|^{p}+\frac{1}{q}\frac{1}{\left(\sum_{k=1}^{n}|b_{k}|^{q}\right)}\sum_{k=1}^{n}|b_{k}|^{q}\\&=\frac{1}{p}+\frac{1}{q}=1\end{align*}
Por lo tanto
\begin{align*}\sum_{k=1}^{n}|a^{\prime}{k}b^{\prime}{k}|\leq 1 &\Rightarrow \sum_{k=1}^{n}|\frac{a_{k}}{A}\frac{b_{k}}{B}|\leq1\\&\Rightarrow \sum_{k=1}^{n}|a_{k}b_{k}|\leq AB\\ &\Rightarrow \sum_{k=1}^{n}|a_{k}b_{k}|\leq \left(\sum_{k=1}^{n}|a_{k}|^{p}\right)^{\frac{1}{p}}\left(\sum_{k=1}^{n}|b_{k}|^{q}\right)^{\frac{1}{q}}\end{align*}
Ahora probaremos la desigualdad de Minkowski
$$\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{\frac{1}{p}}\leq \left[\sum_{k=1}^{n}|a_{k}|^{p}\right]^{\frac{1}{p}}+\left[\sum_{k=1}^{n}|b_{k}|^{q}\right]^{\frac{1}{q}}$$
Tenemos que
\begin{align*}\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}=\sum_{k=1}^{n}|a_{k}+b_{k}|^{p-1}|a_{k}+b_{k}|&\leq \sum_{k=1}^{n}|a_{k}+b_{k}|^{p-1}\left(|a_{k}|+|b_{k}|\right)\\&=\left( \sum_{k=1}^{n}|a_{k}+b_{k}|^{p-1}\right)\left(|a_{k}|\right)+\left(
\sum_{k=1}^{n}|a_{k}+b_{k}|^{p-1}\right)\left(|b_{k}|\right)\end{align*}
Aplicando la desigualdad de Holder a cada sumando tenemos que
\begin{align*}\left(\sum_{k=1}^{n}|a_{k}+b_{k}|^{p-1}\right)\left(|a_{k}|\right)&\leq \left[\sum_{k=1}^{n}a_{k}^{p}\right]^{\frac{1}{p}}\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{q(p-1)}\right]^{\frac{1}{q}}\\&=\left[\sum_{k=1}^{n}a_{k}^{p}\right]^{\frac{1}{p}}\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{\frac{1}{q}}\end{align*}
\begin{align*}\left(\sum_{k=1}^{n}|a_{k}+b_{k}|^{p-1}\right)\left(|b_{k}|\right)&\leq \left[\sum_{k=1}^{n}b_{k}^{p}\right]^{\frac{1}{p}}\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{q(p-1)}\right]^{\frac{1}{q}}\\&=\left[\sum_{k=1}^{n}b_{k}^{p}\right]^{\frac{1}{p}}\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{\frac{1}{q}}\end{align*}
Por lo tanto
$$\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\leq \left[\sum_{k=1}^{n}a_{k}^{p}\right]^{\frac{1}{p}}\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{\frac{1}{q}}+\left[\sum_{k=1}^{n}b_{k}^{p}\right]^{\frac{1}{p}}\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{\frac{1}{q}}$$
Multiplicando ambos miembros de la desigualdad por
$$\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{-\frac{1}{q}}$$
obtenemos
\begin{align*}\left(\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right)\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{-\frac{1}{q}}&=\left(\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right)^{1-\frac{1}{q}}\\&=\left(\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right)^{\frac{1}{p}}\end{align*}
$$\left[\sum_{k=1}^{n}a_{k}^{p}\right]^{\frac{1}{p}}\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{\frac{1}{q}}\left(\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{-\frac{1}{q}}\right)=\left[\sum_{k=1}^{n}a_{k}^{p}\right]^{\frac{1}{p}}$$
$$\left[\sum_{k=1}^{n}b_{k}^{p}\right]^{\frac{1}{p}}\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{\frac{1}{q}}\left(\left[\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right]^{-\frac{1}{q}}\right)=\left[\sum_{k=1}^{n}b_{k}^{p}\right]^{\frac{1}{p}}$$
Por lo tanto $$\left(\sum_{k=1}^{n}|a_{k}+b_{k}|^{p}\right)^{\frac{1}{p}}\leq
\left[\sum_{k=1}^{n}a_{k}^{p}\right]^{\frac{1}{p}}+\left[\sum_{k=1}^{n}b_{k}^{p}\right]^{\frac{1}{p}}$$
Por lo tanto $$\|\overline{x}+\overline{y}\|_{p}\leq \|\overline{x}\|_{p}+\|\overline{y}\|_{p}~\blacksquare$$

Ejemplo. Espacios $\ell_{p}$

Definición. Dado $\bar{x}\in\mathbb{R}^{n}$ definimos
$$\|\bar{x}\|_{p}=\left(\sum_{k=1}^{n}|x_{k}|^{p}\right)^{\frac{1}{p}}~~si~~p\in[1,\infty)$$
Proposición. Dada $p\in[1,\infty)$, consideramos el conjunto $\ell_{p}$ de todas las sucesiones $(x_{k})$ de números reales tales que la serie
$$\sum_{k=1}^{\infty}|x_{k}|^{p}$$converge. Entonces la función
$$\|(x_{k})\|_{p}=\left(\sum_{k=1}^{\infty}|x_{k}|^{p}\right)^{\frac{1}{p}}$$es una norma en $\ell_{p}$
Demostración.
(a) Tenemos
$$\|x_{k}\|_{p}\geq0\Leftrightarrow\left(\sum_{k=1}^{\infty}|x_{k}|^{p}\right)^{\frac{1}{p}}\geq0\Leftrightarrow\sum_{k=1}^{\infty}|x_{k}|^{p}\geq0\Leftrightarrow|x_{k}|^{p}\geq0\Leftrightarrow |x_{k}|\geq0\Leftrightarrow x_{k}\geq0$$
(b) $$\|\lambda x_{k}\|_{p}=\left(\sum_{k=1}^{\infty}|\lambda x_{k}|^{p}\right)^{\frac{1}{p}}=\left(\sum_{k=1}^{\infty}|\lambda|^{p} |x_{k}|^{p}\right)^{\frac{1}{p}}=\left(|\lambda|^{p}\sum_{k=1}^{\infty} |x_{k}|^{p}\right)^{\frac{1}{p}}=|\lambda|\left(\sum_{k=1}^{\infty}|x_{k}|^{p}\right)^{\frac{1}{p}}=|\lambda|~\|x_{k}\|_{p}$$
(c) Como la $\|\|_{p}$ satisface la desigualdad del triángulo, se tiene que
$$\left(\sum_{k=1}^{n} |x_{k}+y_{k}|^{p}\right)^{\frac{1}{p}}\leq \left(\sum_{k=1}^{\infty} |x_{k}|^{p}\right)^{\frac{1}{p}}+\left(\sum_{k=1}^{\infty} |y_{k}|^{p}\right)^{\frac{1}{p}}\leq\|x_{k}\|_{p}+\|y_{k}\|_{p}$$
para todo $n\in \mathbb{N}$. En consecuencia, la serie
$$\sum_{k=1}^{\infty} |x_{k}+y_{k}|^{p}$$
converge y se cumple que
$$\|x_{k}+y_{k}\|_{p}=\left(\sum_{k=1}^{\infty} |x_{k}+y_{k}|^{p}\right)^{\frac{1}{p}}\leq\|x_{k}\|_{p}+\|y_{k}\|_{p}.~~\textcolor{orange}{\blacksquare}$$
Proposición. Sea $\bar{x}\in\mathbb{R}^{n}$, entonces
$$\|\bar{x}\|_{\infty}\leq\|\bar{x}\|\leq\|\bar{x}\|_{1}\leq n\|\bar{x}\|$$

Demostración. Sea $|x_{k}|=\max{|x_{1},…,|x_{n}||}$
Se tiene entonces
$$|x_{k}|=\sqrt{x_{k}^{2}}\leq \sqrt{x_{1}^{2}+…+x_{n}^{2}}=\|\bar{x}\|$$
$\therefore~~\|\bar{x}\|_{\infty}\leq\|\bar{x}\|$
Ahora bien
$$\left(\|\bar{x}\|\right)^{2}=\left(|x_{1}|^{2}+…+|x_{n}|^{2}\right)\leq \sum_{i=1}^{n}|x_{i}|^{2}+2\sum_{i\leq i\leq j\leq n}|x_{i}||x_{j}|=\left(|x_{1}|+…+|x_{n}|\right)^{2}=\left(\|\bar{x}\|_{1}\right)^{2}$$
$$~\Rightarrow~\left(\|\bar{x}\|\right)^{2}\leq\left(\|\bar{x}\|_{1}\right)^{2}$$
$$~\Rightarrow~\|\bar{x}\|\leq \|\bar{x}\|_{1}$$
También si suponemos que $|x_{j}|=\max{|x_{1}|,…,|x_{n}|}$ entonces
$$\|\bar{x}\|_{1}=|x_{j}|\leq |x_{j}|+…+|x_{j}|=n|x_{j}|=n\max{|x_{1}|,…,|x_{j}|}=n\|\bar{x}\|_{\infty}$$
por lo que
$$\|\bar{x}\|_{1}\leq n\|\bar{x}\|_{\infty}.~~ \blacksquare$$

Proposición. Sea $\bar{x}\in\mathbb{R}^{n}$ entonces
$$\|\bar{x}\|_{\infty}\leq\|\bar{x}\|\leq\sqrt{n}\|\bar{x}\|_{\infty}$$
Demostración. Suponemos que $|x_{j}|=\max{|x_{1}|,…,|x_{n}|}$. Se tiene entonces
$$|x_{j}|=\sqrt{x_{j}^{2}}\leq \sqrt{x_{1}^{2}+…+x_{j}^{2}+…+x_{n}^{2}}=\|\bar{x}\|$$
Por tanto
$$\|\bar{x}\|_{\infty}\leq\|\bar{x}\|$$
Por otro lado suponemos que $|x_{j}|=\max{|x_{1}|,…,|x_{n}|}$ y tenemos
$$\|\bar{x}\|=\sqrt{x_{1}^{2}+…+x_{j}^{2}+…+x_{n}^{2}}\leq \sqrt{x_{j}^{2}+…+x_{j}^{2}+…+x_{j}^{2}}=\sqrt{n(x_{j}^{2})}=\sqrt{n}\|\bar{x}\|_{\infty}$$
por lo tanto
$$\|\bar{x}\|\leq\sqrt{n}\|\bar{x}\|_{\infty}.~~\blacksquare$$

Proposición. Sea $\bar{x}\in\mathbb{R}^{n}$ entonces
$$\|\bar{x}\|_{1}\leq\sqrt{n}\|\bar{x}\|$$
Demostración.
$$\|\bar{x}\|_{1}=|x_{1}|+…+|x_{n}|=\left(1,…,1\right)\cdot (|x_{1}|,…,|x_{1}|)\leq \|(1,…,1)\|~\|\bar{x}\|=\sqrt{n}\|\bar{x}\|$$
por lo tanto
$$\|\bar{x}\|_{1}\leq\sqrt{n}\|\bar{x}\|.~~\blacksquare$$

Ortogonalidad de vectores

Generalizando el concepto de perpendicularidad en $\mathbb{R}^{3}$, damos la siguiente definición.
Definición. Sea E un espacio vectorial dotado de un producto escalar $\langle,\rangle$, se dice que dos vectores $\overline{x},\overline{y}\in E$ son ortogonales si $$\langle \overline{x},\overline{y}\rangle=0$$
Tenemos que si $\langle \overline{x},\overline{y}\rangle=0$ entonces $$\|\overline{x}-\overline{y}\|^{2}=\langle \overline{x}+\overline{y},\overline{x}+\overline{y}\rangle=\langle \overline{x},\overline{x}\rangle-2\langle \overline{x},\overline{y}\rangle+\langle \overline{y},\overline{y}\rangle=\langle \overline{x},\overline{x}\rangle+\langle \overline{y},\overline{y}\rangle=\|\overline{x}\|^{2}+\|\overline{y}\|^{2}$$
es decir se cumple el teorema de pitagoras.

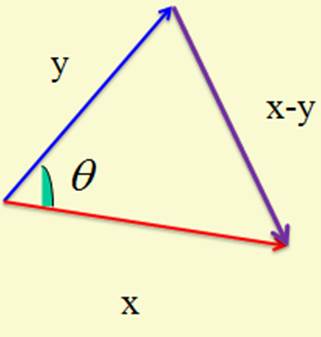
Sean ahora $\overline{x},\overline{y}\in \mathbb{R}^{2}$ y sea $\theta$ el ángulo entre ellos. Según la ley de los cosenos
\begin{align*} \|\overline{x}-\overline{y}\|^{2}&=\|\overline{x}\|^{2}+\|\overline{y}\|^{2}-2\|\overline{x}\|\|\overline{y}\|\cos(\theta) \\ &~\Rightarrow~\|\overline{x}\|^{2}-2\langle \overline{x},\overline{y}\rangle+\|\overline{y}\|^{2}=\|\overline{x}\|^{2}+\|\overline{y}\|^{2}-2\|\overline{x}\|\|\overline{y}\|\cos(\theta) \\ &~\Rightarrow~\langle \overline{x},\overline{y}\rangle=\|\overline{x}\|\|\overline{y}\|\cos(\theta) \end{align*}
Esta fórmula motiva la siguiente definición de ángulo $\theta$ entre dos vectores no nulos $\overline{x},\overline{y}\in E$, por medio de $$\boxed{\theta=\arccos\left(\frac{\langle \overline{x},\overline{y}\rangle}{|\overline{x}||\overline{y}|}\right)}$$

.

Más adelante

Como vimos en este apartado el concepto de norma nos permite relacionar la idea de longitud de un vector respecto al origen. De forma más extensa nos ayudará a relacionar la idea de longitud entre dos vectores como una distancia subyacente entre esos dos objetos.

Tarea moral

1.- Dada $f\in C^0[a,b]$ demuestra que $\left\| f\right\| _{p}= (\int _a^b |f(x)|^pdx)^{1/p}$ si $p \in [1,\infty)$ si $p\in [1,\infty)$ es una norma.

2.- Demuestra que $\left\| f\right\|_{\infty}=max\{|f(x)|:a\leq x\leq b \}$ es una norma .

3.- Sea $f\in C^0[a,b]$ y $p\in [1,\infty]$ demuestra que $\left\| f\right\|_p=0$ sí y solo si $f=0$.
4.- Demuestra la desigualdad de Minkowski para integrales. Si $p\in[1,\infty]$ entonces $\left\| f + g \right\|\leq | f | + |g| $ $\forall f,g\in C^0[a,b]$

5.- Expresa el siguiente caso al vector a como la suma de un vector paralelo al vector b y uno ortogonal. Donde $a=(1,2,3)$, $b=(1,0,0)$.