Introducción
Esta es la primera entrada de las notas de curso correspondientes a la materia de Probabilidad I. En esta sesión, platicaremos primero un poco sobre el objeto de estudio de la probabilidad. Después, un poco sobre su filosofía. Es decir, las ideas que sigue. Finalmente, presentaremos algunos de los conceptos matemáticos más fundamentales en esta teoría.
Antes de dar comienzo a nuestro tratamiento de la probabilidad, considero prudente incluir los conocimientos previos recomendables para este curso.
Sobre los prerrequisitos
Primeramente, debes de tener bien claros los contenidos de un curso de Álgebra Superior I. Pon especial atención a los temas de lógica, de teoría de conjuntos, y de funciones.
Por otro lado, te recomiendo que tengas bien claros los temas de un curso de Cálculo Diferencial e Integral II. En este curso es donde se abordan los temas de integración de funciones (de acuerdo con la teoría de integración de Riemann).
Por último, es deseable que tengas una buena noción de los temas de un curso de Cálculo Diferencial e Integral I. En particular, es importante que tengas claros los temas de sucesiones y de diferenciación.
A lo largo de estas notas supondré que manejas bien estos temas. Sin embargo, si necesitas revisarlos, puedes recurrir a nuestras notas de curso para Álgebra Superior I, Cálculo Diferencial e Integral I y Cálculo Diferencial e Integral II.
Fenómenos Aleatorios
En la teoría de la probabilidad nos interesa describir matemáticamente los fenómenos aleatorios. Aquí nos topamos con una primera pregunta: ¿qué es un fenómeno aleatorio? A grandes rasgos, un fenómeno aleatorio es todo aquel fenómeno cuyo resultado se conoce únicamente hasta que este ha concluido.
Por ejemplo, si tomas una moneda y la lanzas al aire, ¿puedes saber con anterioridad cuál de sus caras caerá arriba? A menos que seas clarividente, la respuesta es no. Así, el lanzamiento de una moneda puede pensarse como un fenómeno aleatorio. Conocerás su resultado únicamente hasta que el lanzamiento haya concluido. Otro ejemplo, de naturaleza más trágica, son los terremotos. La fecha exacta del siguiente terremoto se sabrá hasta que este ocurra. En consecuencia, la ocurrencia de un terremoto es un fenómeno aleatorio.
Un Poco de la Filosofía de la Probabilidad
Seguramente conoces ramas de la matemática que se esfuerzan por describir el comportamiento de los fenómenos de la naturaleza de la manera más precisa posible. Sin embargo, tal no es el caso de la probabilidad. En nuestro caso, orientaremos nuestros esfuerzos en describir cómo se acomodan (o se distribuyen) los resultados de un fenómeno aleatorio.
De lo anterior probablemente te surgen dos interrogantes. En primera instancia, ¿A qué te refieres por «cómo se acomodan»? Y en segunda, ¿cómo que la probabilidad no se esfuerza por describir el comportamiento de la naturaleza? Para contestar a la primera pregunta, toma una moneda. Lánzala 10 veces al aire, y registra los resultados. Hice este ejercicio por mi cuenta, y la siguiente tabla ilustra cuáles lanzamientos salieron «águila» (A) y cuáles «sol» (S):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| A | S | S | S | A | A | S | S | S | A |
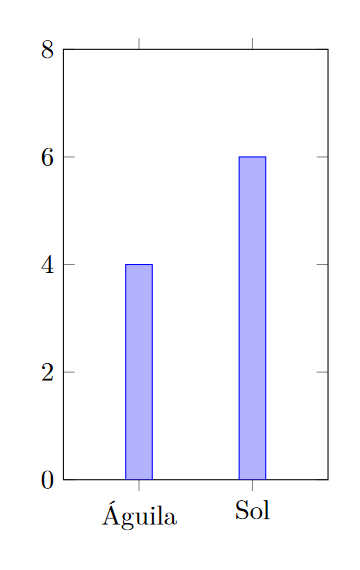
Estos resultados pueden acomodarse también en una gráfica como la siguiente:
Donde la altura de cada barra representa la frecuencia del resultado correspondiente. De mis 10 realizaciones del lanzamiento, 4 salieron «águila» y 6 salieron «sol». Esta gráfica exhibe cómo se distribuyeron los resultados de mis 10 lanzamientos de moneda. Puedes replicar esta gráfica con los resultados de tus 10 lanzamientos. Con ello, te darás una idea de cómo se distribuyen sus resultados.
En el siguiente vídeo se observa otro ejemplo de la distribución que siguen los resultados de un fenómeno aleatorio:
El juguete ilustrado en el vídeo es conocido como Máquina de Galton. En inglés, Galton Board. Se dejan caer muchas pelotitas desde el compartimiento de arriba. Estas rebotan aleatoriamente de izquierda a derecha hasta que caen en alguno de los compartimientos de abajo. Así, las barras resultantes representan cómo se distribuyen los resultados de dejar caer las pelotitas.
Burdamente, la «manera en la que se distribuyen» los resultados de un fenómeno aleatorio se refiere a la frecuencia con la que estos ocurren en varias realizaciones del fenómeno.
Justificando la Filosofía de la Probabilidad
Ahora, vamos a abordar un poco del aspecto filosófico de la probabilidad. Anteriormente, te mencioné que la probabilidad no se enfoca en modelar matemáticamente el funcionamiento de los fenómenos de la naturaleza. Para entender esto, quiero que pienses en lo siguiente:
Si yo te preguntara «¿cómo le hiciste para que tu lanzamiento saliera «águila»? ¿Y para que saliera «sol»?», ¿serías capaz de dar respuesta a alguna de las dos preguntas? Piénsalo bien. Al realizar los lanzamientos, seguramente acomodaste la mano a una cierta altura, y en alguna posición. Después, acomodaste la moneda en tu mano. Acto seguido, la lanzaste (con un cierto ángulo), y finalmente la moneda cayó sobre alguna de sus caras. Toda esta información es relevante para determinar el resultado de un lanzamiento. ¿Serías capaz de decirme la información de los lanzamientos donde salió «águila»? ¿Y de los que salió «sol»? Incluso si tuviéramos el equipo tecnológico para capturar esa información, ¿hace diferencia?
La respuesta es que no. Si ya capturaste estos valores, es porque el experimento ya está ocurriendo. Más aún, quizás ya hasta concluyó. Así, incluso si tuvieras un modelo matemático muy preciso para describir el lanzamiento de una moneda, no resulta útil para predecir su resultado.
Esta discusión puede extenderse a otros fenómenos aleatorios, y justifica el objeto de estudio de la probabilidad: describir matemáticamente el comportamiento de los resultados de un fenómeno aleatorio.
Describiendo Matemáticamente los Fenómenos Aleatorios
Ya quedó clara nuestra intención de centrar nuestra atención en los resultados de un experimento aleatorio. A partir de aquí, empieza la labor matemática. Para comenzar, partiremos de un conjunto cuyos elementos son todos los posibles resultados de un fenómeno aleatorio.
Definición. Dado un fenómeno o experimento aleatorio, el espacio muestral de dicho fenómeno es el conjunto cuyos elementos son todos los posibles resultados del fenómeno, y será denotado por $\Omega$ (Omega).
Ejemplos. El espacio muestral del lanzamiento de una moneda podría ser
$$\Omega = \left\lbrace \text{águila}, \text{sol} \right\rbrace,$$
o alternativamente, podemos hacer uso de números para representar estos resultados
$$\Omega = \left\lbrace 0, 1\right\rbrace,$$
y puedes escoger cuál es cuál (por ejemplo, que $0$ es águila y $1$ es sol).
En el caso del lanzamiento de un dado, podemos considerar el espacio muestral
$$\Omega = \left\lbrace 1, 2, 3, 4, 5, 6 \right\rbrace.$$
Si lanzamos dos dados simultáneamente, podemos considerar que el espacio muestral de ese experimento es
$$\Omega = \left\lbrace 1, 2, 3, 4, 5, 6 \right\rbrace \times \left\lbrace 1, 2, 3, 4, 5, 6 \right\rbrace,$$
pues nos interesan todas las combinaciones de valores que puede tomar cada dado. Por ejemplo, $(1,3)$ representa al resultado en el que el primer dado cae $1$, y el segundo, $2$.
Nuestra intención será cuantificar qué tan probable es que ocurra uno o más de estos resultados. Esto lo haremos asignando una «calificación» entre 0 y 1 a ciertos subconjuntos importantes de $\Omega$. Así, la «calificación» será 0 para lo más improbable, y 1 para lo más probable. Pero, ¿a qué me refiero por subconjuntos importantes? Veámoslo.
Álgebras
Nuestra intención es «calificar» qué tan probable es alguno de los resultados de nuestro fenómeno aleatorio. Es decir, queremos medir la probabilidad de ocurrencia de los resultados. Como queremos realizar una asignación, será necesaria una función, digamos, $\mathbb{P}$. Esta función asignará el número $\mathbb{P}(A)$ a cada conjunto $A$ de una cierta familia de conjuntos. Debido a esto, la familia sobre la que se define a $\mathbb{P}$ debe de tener una cierta estructura. Para motivar el tipo de estructura que impondremos, podemos valernos de ciertas consideraciones de la probabilidad.
Si $\Omega$ es el espacio muestral de un fenómeno aleatorio, dado $A \subseteq \Omega$, y dado $\omega \in \Omega$, es natural preguntar «¿es cierto que $\omega \in A$?» y encontrar si la respuesta es sí o no una vez que $\omega$ ha sido observado. Ahora, si pudimos responder la pregunta anterior, podemos responder si «¿es cierto que $\omega \in A^{\textsf{c}}$?» Más aún, si dado $n \in \mathbb{N}^{+}$ (el conjunto de los números naturales sin el $0$), para cada $i \in \{1, \ldots, n\}$ podemos determinar la veracidad de $\omega \in A_{i}$, deberíamos de poder determinar si $\omega \in \bigcup_{i=1}^{n}A_{i}$ y $\omega \in \bigcap_{i=1}^{n}A_{i}$.
Por lo tanto, un primer requisito estructural para la familia sobre la que definiremos a $\mathbb{P}$ es que sea cerrada bajo complementación, unión finita e intersección finita.
Además, como la respuesta a la pregunta «¿es cierto que $\omega \in \Omega$?» es siempre «sí», el espacio muestral mismo debería de ser un elemento de la familia. Así, esta discusión da lugar a la siguiente definición.
Definición. Sea $\mathscr{F}$ una colección de subconjuntos de un conjunto $\Omega$ (i.e. $\mathscr{F} \subseteq \mathscr{P}(\Omega)$). Diremos que $\mathscr{F}$ es un álgebra sobre $\Omega$ si cumple las siguientes propiedades:
- $\Omega \in \mathscr{F}$.
- Si $A \in \mathscr{F}$, entonces $A^{\mathsf{c}} \in \mathscr{F}$.
- Si $A_{1}, A_{2}, \ldots, A_{n} \in \mathscr{F}$, entonces $\bigcup_{i=1}^{n} A_{i} \in \mathscr{F}$.
$A^{\mathsf{c}}$ es el complemento de $A$ respecto a $\Omega$, pues $A \subseteq \Omega$.
La propiedad 2 es conocida como cerradura bajo complementación, y la propiedad 3 como cerradura bajo uniones finitas. De la definición de álgebra es posible deducir que un álgebra es también cerrado bajo intersecciones finitas (véase la tarea moral al final de esta entrada).
σ-álgebras
Hay una propiedad un poco más exigente que no es tan sencilla de justificar. En la definición de un álgebra, ¿deberíamos de pedir en la propiedad 3 que sea cerrada bajo uniones numerables? El argumento más convincente para hacerlo es que la teoría matemática resultante es más vasta. Así, obtenemos la siguiente definición.
Definición. Sea $\mathscr{F}$ una colección de subconjuntos de un conjunto $\Omega$ (es decir, $\mathscr{F} \subseteq \mathscr{P}(\Omega)$). Diremos que $\mathscr{F}$ es un σ–álgebra sobre $\Omega$ (se lee «sigma-álgebra sobre omega», su plural es «sigma-álgebras») si cumple las siguientes propiedades:
- $\Omega \in \mathscr{F}$.
- Si $A \in \mathscr{F}$, entonces $A^{\mathsf{c}} \in \mathscr{F}$.
- Si $A_{1}, A_{2}, \ldots \in \mathscr{F}$, entonces $\bigcup_{i=1}^{\infty} A_{i} \in \mathscr{F}$.
$A^{\mathsf{c}}$ es el complemento de $A$ respecto a $\Omega$, pues $A \subseteq \Omega$.
En el contexto de la probabilidad, los elementos de un σ-álgebra son llamados eventos.
La propiedad 3 es conocida como cerradura bajo uniones numerables. Del mismo modo que con un álgebra, es posible deducir que un σ-álgebra es cerrado bajo intersecciones numerables.
Ejemplos. Dado $\Omega$ un conjunto cualquiera, su conjunto potencia $\mathscr{P}(\Omega)$ es un σ-álgebra sobre $\Omega$. Recordemos que
$$\mathscr{P}(\Omega) = \left\lbrace x \mid x \subseteq \Omega \right\rbrace.$$
Así, para ver que $\mathscr{P}(\Omega)$ es un σ-álgebra, debemos de verificar que cumple las tres propiedades de un σ-álgebra.
- Sabiendo que $\Omega \subseteq \Omega$, queda demostrado que $\Omega \in \mathscr{P}(\Omega)$.
- Sea $A \in \mathscr{P}(\Omega)$. Queremos demostrar que $A^{\mathsf{c}} \in \mathscr{P}(\Omega)$. Debido a que $A \in \mathscr{P}(\Omega)$, se sigue que $A \subseteq \Omega$. Debido a que $A^{\mathsf{c}}$ es el complemento de $A$ respecto a $\Omega$, este complemento está bien definido, y por lo tanto, $A^{\mathsf{c}} = \Omega \smallsetminus A$. Como $\Omega \smallsetminus A \subseteq \Omega$, se sigue que $A^{\mathsf{c}} \subseteq \Omega$. Es decir, $A^{\mathsf{c}} \in \mathscr{P}(\Omega)$.
- Sean $A_{1}, A_{2}, \ldots \in \mathscr{P}(\Omega)$. Debemos demostrar que $\bigcup_{i=1}^{\infty} A_{i} \in \mathscr{P}(\Omega)$. Sabiendo que $A_{1}, A_{2}, \ldots \in \mathscr{P}(\Omega)$, podemos ver que
$$\forall i \in \mathbb{N}^{+}: A_{i} \subseteq \Omega.$$ Sea $a \in \bigcup_{i=1}^{\infty} A_{i}$. Esto implica que existe $n \in \mathbb{N}^{+}$ tal que $a \in A_{n}$. Por lo anterior, sabemos que $A_{n} \subseteq \Omega$, y en consecuencia, $a \in \Omega$. Como la elección de $a$ fue arbitraria, queda demostrado que $\bigcup_{i=1}^{\infty} A_{i} \subseteq \Omega$, y por lo tanto, $\bigcup_{i=1}^{\infty} A_{i} \in \mathscr{P}(\Omega)$.
Considerando nuevamente a $\Omega$ un conjunto cualquiera, el conjunto $\mathscr{F} = \{ \emptyset, \Omega \}$ es un σ-álgebra. La demostración de este hecho es muy sencilla, y se deja como tarea moral.
Para un ejemplo más explícito, considera a $\Omega$ como el siguiente conjunto.
\[ \Omega = \{ 1, 2, 3, 4, 5, 6 \}. \]
Sea $\mathscr{F}$ el siguiente conjunto:
\[ \mathscr{F} = \{ \emptyset, \{1, 3, 5\}, \{2, 4, 6\}, \{ 1, 2, 3, 4, 5, 6 \} \}. \]
Podemos ver que $\mathscr{F}$ es un σ-álgebra. Observa que $\{ 1, 2, 3, 4, 5, 6 \}$ es uno de los elementos de $\mathscr{F}$, así que cumple la primera propiedad. Después, para ver que cumple la segunda propiedad, hay que ver que para cada $A \in \mathscr{F}$ se cumple que $A^{\mathsf{c}} \in \mathscr{F}$. Para verlo, hay que revisar que se cumple para cada elemento de $\mathscr{F}$ satisface esa propiedad.
- Para $\emptyset$, $\emptyset^{\mathsf{c}} = \Omega$, el cual ya vimos que es un elemento de $\mathscr{F}$.
- Para $\{1, 3, 5\}$, observa que $\{1, 3, 5\}^{\mathsf{c}} = \{2, 4, 6\}$, el cual vemos que es uno de los elementos de $\mathscr{F}$.
- Similarmente, también se cumple para $\{2, 4, 6\}$, pues $\{2, 4, 6\}^{\mathsf{c}} = \{1, 3, 5\}$, que efectivamente es uno de los elementos de $\mathscr{F}$.
- Finalmente, para $\Omega$, se tiene que $\Omega^{\mathsf{c}} = \emptyset$, que también es uno de los elementos de $\mathscr{F}$.
Así, vemos que $\mathscr{F}$ satisface la segunda propiedad de un σ-álgebra. Finalmente, observa que $\mathscr{F}$ es un conjunto finito. En consecuencia, no podemos escoger una familia infinita numerable de elementos de $\mathscr{F}$. Así, para demostrar la tercera propiedad de un σ-álgebra en una familia finita de conjuntos, basta demostrar que se cumple la cerradura bajo uniones de dos conjuntos.
Esto lo podemos hacer porque si demostramos que es cerrada para uniones de dos conjuntos, digamos, que para cualesquiera $A, B \in \mathscr{F}$ se cumple $A \cup B \in \mathscr{F}$, entonces si $A$, $B$ y $C$ son conjuntos tales que $A \cup B, C \in \mathscr{F}$, entonces $(A \cup B) \cup C \in \mathscr{F}$. Es decir, la cerradura bajo uniones de dos conjuntos implica la cerradura bajo uniones de tres conjuntos. Similarmente, esta última implica la cerradura bajo uniones de cuatro, y esta la cerradura bajo uniones de cinco… Y así sucesivamente.
Bien, entonces veamos que se cumple la cerradura de uniones de cualesquiera dos conjuntos de $\mathscr{F}$.
- Las uniones de cualquier elemento de $\mathscr{F}$ con $\emptyset$ son nuevamente un elemento de $\mathscr{F}$, pues si $A \in \mathscr{F}$, entonces $A \cup \emptyset = \emptyset \cup A = A \in \mathscr{F}$.
- Veamos los casos para $\{ 1, 3, 5 \}$:
- $\{1, 3, 5\} \cup \{ 2, 4, 6 \} = \{1, 2, 3, 4, 5, 6 \} \in \mathscr{F}$, así que se cumple la cerradura.
- $\{1, 3, 5\} \cup \{ 1, 2, 3, 4, 5, 6 \} = \{1, 2, 3, 4, 5, 6\} \in \mathscr{F}$, también se cumple la cerradura.
- Ahora, los casos para $\{ 2, 4, 6 \}$:
- $\{2, 4, 6\} \cup \{1,3,5\} = \{1, 2, 3, 4, 5, 6\} \in \mathscr{F}$, se cumple la cerradura.
- $\{2, 4, 6\} \cup \{1, 2, 3, 4, 5, 6\} = \{1, 2, 3, 4, 5, 6\} \in \mathscr{F}$, también se cumple.
- El caso para $\{1, 2, 3, 4, 5, 6 \}$ es parecido al de $\emptyset$, pues para cualquier $A \in \mathscr{F}$ se cumple que $A \cup \{1, 2, 3, 4, 5, 6 \} = \{1, 2, 3, 4, 5, 6\} \cup A = \{1, 2, 3, 4, 5, 6\} \in \mathscr{F}$, ya que todos los elementos de $\mathscr{F}$ son subconjuntos de $\Omega$.
Un último ejemplo más interesante
Sea $\Omega = \mathbb{R}$, el conjunto de los números reales. Considera a los siguientes conjuntos:
\begin{align*}
J_{1} &= \left\lbrace (a,b] \mid a \in \mathbb{R} \land b \in \mathbb{R} \land a < b \right\rbrace, \\
J_{2} &= \left\lbrace (-\infty,a] \mid a \in \mathbb{R} \right\rbrace, \\
J_{3} &= \left\lbrace (a, \infty) \mid a \in \mathbb{R} \right\rbrace.
\end{align*}
Es decir, $J_{1}$ es el conjunto cuyos elementos son todos los intervalos acotados, semi-cerrados por la derecha. Por otro lado, $J_{2}$ es el conjunto de intervalos cerrados por la derecha, y sin cota inferior. Finalmente, $J_{3}$ es el conjunto que tiene por elementos a todos los intervalos abiertos por la izquierda, y sin cota superior.
A partir de $J_{1}$, $J_{2}$ y $J_{3}$, definamos el siguiente conjunto:
\[ J = J_{1} \cup J_{2} \cup J_{3}. \]
El conjunto $J$ simplemente junta a todos los tipos de intervalos descritos más arriba. Después, para cada $n \in \mathbb{N}$, definamos los siguientes conjuntos auxiliares:
\[ B_{n} = \left\lbrace \bigcup_{i=1}^{n} A_{i} \; \middle| \; \forall i,j \in \left\lbrace 1, \ldots, n \right\rbrace : (A_{i} \in J \land (i \neq j \implies A_{i} \cap A_{j} = \emptyset)) \right\rbrace. \]
Esto es, para cada $n \in \mathbb{N}$, $B_{n}$ es el conjunto cuyos elementos son subconjuntos de $\mathbb{R}$ tales que son el resultado de hacer la unión de exactamente $n$ intervalos ajenos de $J$. Por ejemplo, $B_{1}$ son los subconjuntos de $\mathbb{R}$ que resultan de unir exactamente $1$ intervalo de $J$. Es decir, es el mismo $J$. $B_{2}$ son los subconjuntos de $\mathbb{R}$ que resultan al unir exactamente $2$ intervalos ajenos de $J$. Y así, sucesivamente. Como convención, $B_{0} = \{ \emptyset \}$, pues $\emptyset$ es el único subconjunto de $\mathbb{R}$ que resulta de unir $0$ intervalos.
Ahora, considera el siguiente conjunto $\mathscr{F}$:
\[ \mathscr{F} = \bigcup_{n=0}^{\infty} B_{n}. \]
Así, $\mathscr{F}$ es el conjunto cuyos elementos son todas las uniones finitas de intervalos ajenos en $J$. Es posible (e interesante) demostrar que $\mathscr{F}$ es un álgebra de subconjuntos de $\mathbb{R}$. Sin embargo, $\mathscr{F}$ no es un σ-álgebra. Por ejemplo, si para cada $n \in \mathbb{N}^{+}$ tomamos los conjuntos $E_{n} = (0, 1 – (1/n)]$, vemos que en $E_{1}, E_{2}, \ldots \in \mathscr{F}$, pero $\bigcup_{n=1}^{\infty} E_{n} = (0,1) \notin \mathscr{F}$.
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu manejo de los conceptos abordados en esta entrada.
- Sea $\Omega = \{ 1, 2, 3, 4, 5, 6 \}$. Determina si las siguientes familias de subconjuntos de $\Omega$ son σ-álgebras.
- $\mathscr{F}_{1} = \{ \emptyset, \{ 1, 2 \}, \{3, 4\}, \{3, 4, 5, 6\}, \{1, 2, 5, 6 \}, \{1, 2, 3, 4, 5, 6 \} \}$.
- $\mathscr{F}_{2} = \{ \emptyset, \{1\}, \{3\}, \{1,3\}, \{2,3,4,5,6\}, \{1,2,4,5,6\}, \{2,4,5,6\}, \{1,2,3,4,5,6\}\}.$
- A partir de la definición de álgebra, demuestra que si $\mathscr{F}$ es un álgebra sobre $\Omega$, entonces también cumple las siguientes propiedades:
- $\emptyset \in \mathscr{F}$.
- Si $A_{1}, A_{2}, \ldots A_{n} \in \mathscr{F}$, entonces $\bigcap_{i=1}^{n} A_{i} \in \mathscr{F}$ (sugerencia: aprovecha las propiedades 2 y 3 de un álgebra, y recurre a las leyes de De Morgan).
- Si $A, B \in \mathscr{F}$, entonces:
- $B \smallsetminus A \in \mathscr{F}$.
- $A \triangle B \in \mathscr{F}$.
- A partir de la definición σ-álgebra, demuestra que si $\mathscr{F}$ es un σ-álgebra sobre $\Omega$, entonces también cumple las siguientes propiedades:
- $\mathscr{F}$ es un álgebra.
- Si $A_{1}, A_{2}, \ldots \in \mathscr{F}$, entonces $\bigcap_{i=1}^{\infty} A_{i} \in \mathscr{F}$ (sugerencia: aprovecha las propiedades 2 y 3 de un σ-álgebra, y recurre a las leyes de De Morgan).
- Demuestra que dado $\Omega$ un conjunto cualquiera, el conjunto $\mathscr{F} = \{ \emptyset, \Omega \}$ es un σ-álgebra sobre $\Omega$.
- Si $\Omega$ es un conjunto finito, ¿es posible construir un álgebra que no sea σ-álgebra?
Más adelante…
En esta entrada definimos dos de las piedras angulares de la teoría de la probabilidad, el espacio muestral y los σ-álgebras. Por un lado, el espacio muestral deja claro cuáles son los posibles resultados de un experimento aleatorio. Por otra parte, un σ-álgebra del espacio muestral es el que determina los conjuntos que podremos medir. En la siguiente entrada abordaremos la construcción de σ-álgebras a partir de una colección dada de subconjuntos de $\Omega$. Con ello, veremos un σ-álgebra muy importante que puede ser construido de distintas maneras. En particular, puede hacerse utilizando el álgebra de nuestro último ejemplo.
Entradas relacionadas
- Ir a Probabilidad I
- Siguiente entrada del curso: Construcción de σ-álgebras