Introducción

Este concepto, se usa cuando las instituciones de crédito, como los bancos, otorgan préstamos y esta herramienta, facilita mucho la forma de cómo describir el comportamiento del pago de una deuda, a través del tiempo. En términos generales, es un tipo de registro que desglosa de manera detallada cada uno de los conceptos que conforman el pago, tales como interés, periodos, cantidad que se paga directo a la deuda, así como el saldo pendiente por liquidar. En este apartado se analizará la forma en que se construye una tabla de amortización, algunas de sus tipos, además; se podrán hacer uso de las anualidades.

Concepto y forma de construir una tabla de amortización

El significado de la palabra amortización, tiene su origen en el latín, la cual significa mort, muerte, y tiene su relación con las matemáticas financieras ya que es una forma de asociar el término de una deuda, misma que estará regida por los conceptos que se han venido trabajando casi en todos los temas, tales como una tasa de interés, un plazo, pagos cada cierto tiempo, etc.

A cualquier operación financiera, se le puede construir una tabla de amortización, ejemplos como el adquirir una casa, un departamento, un automóvil, a crédito, que tenga que ver con una deuda, siempre podremos obtener una forma de pago que deberá ser amortizada.

Recordando un poco lo que se ha estudiado, cuando los pagos que se van a destinar para saldar un préstamo, y se hace uso de alguna de las anualidades que se han visto, sea cual sea la anualidad, todos tienen una forma predeterminada de hacerlos.

Lo anterior, nos permite observar que cuando usamos anualidades, se determina la forma en que se van a hacer los pagos, y a partir de éstas, quedan programados cada cierto tiempo, es bajo este supuesto que en el concepto de tabla de amortización se puede visualizar las cantidades del pago que se destinan a el pago de la deuda, al pago de intereses, la cantidad de pagos que falta por realizar, así como el saldo que aún falta por liquidar.

Es importante hacer mención, que al igual que como se manejó en los diferentes tipos de anualidades, también en las tablas de amortización se puede dar la combinación entre éstas, esto se traduce, a que las cantidades que se destinen para el pago de interés, de capital, que son variables que igual aparecen en las anualidades, también se verán afectados, por lo que no podrán siempre ser las mismas, irán variando dependiendo de las cláusulas que se pacten entre las partes involucradas.

Sin embargo, también es posible que se fijen todas las variables, y en tal caso se podrá tener la cantidad que ascenderá cada uno de los pagos. En cambio, cuando las tasas sean variables, por ejemplo, sólo se podrá conocer cuando se conozca el valor de la tasa de interés. Esto ocurre, cuando en algunos créditos se escoge una tasa de interés (conocida como tasa de referencia, la cual tiene la característica de que se le agregan puntos porcentuales para determinarla), que, por su naturaleza, su valor puede estar cambiando todos los días, cada semana o cada mes.

A continuación, se muestran los diferentes tipos de tablas de amortización que se pueden obtener para hacer el pago de un préstamo:

En la mayoría de los créditos, cuyos pagos se calculen a través de alguna anualidad, se les proporciona una tabla que contiene, cada uno de los periodos que dura el contrato, además indica la cantidad que se aporta en cada pago, el porcentaje que se destina a pago de intereses, la cantidad que se destina en cada pago para liquidar la deuda, la cantidad de pagos que conforman el crédito, y la cantidad que falta por pagar para poder liquidarlo en su totalidad.

Dicha tabla, recibe el nombre de tabla de amortización, muy útil, porque permite visualizar por cada periodo la forma en que se va pagando el crédito, incluso nos permite saber la cantidad exacta que se debe, cuando se decida pagar antes el crédito, porque nos muestra el saldo insoluto (cantidad que aún se debe hasta ése periodo).

Para realizar la primera tabla de amortización, se hará uso del siguiente ejemplo:

Un banco otorga un crédito a Julia por la cantidad de \$80,000 pesos, la cual se pretende pagar en 10 mensualidades vencidas, con una tasa de interés del 5% efectivo mensual.

En primer lugar, se procederá a obtener el monto de los pagos, haciendo uso de la siguiente ecuación:

$$80,000=X\prescript{}{10}{\mathbf{A}}_{0.05}$$

$$80,000=X\left(\frac{1-\left(\frac{1}{\left(1+0.05\right)^{10}}\right)}{0.05}\right)$$

$$X=\frac{80,000}{7.7217349}=10,360.366$$

El pago asciende a $10,360.366$

En cada columna se describe la información que representa cada uno de los valores que se van a desglosar.

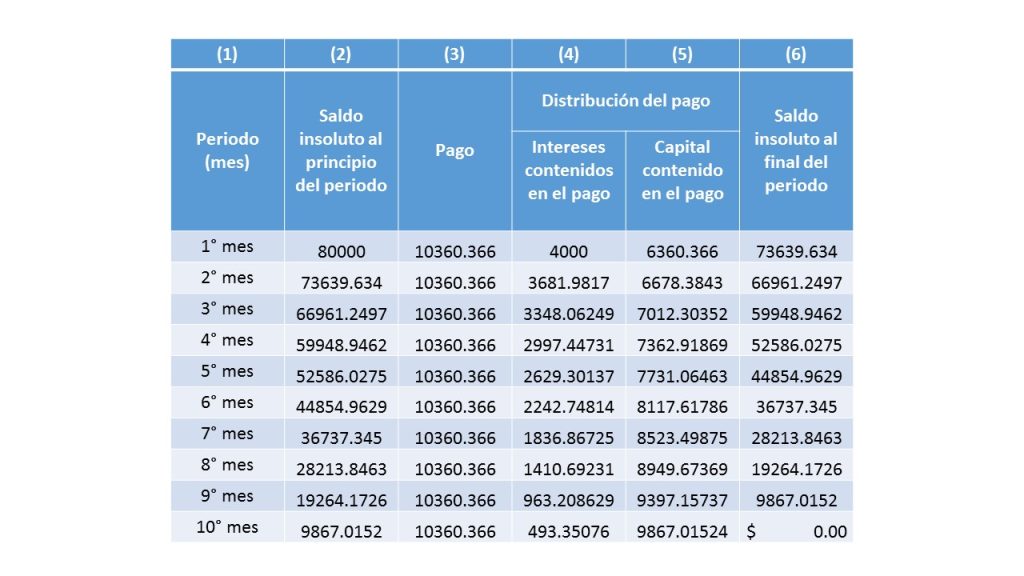
En la primer columna, se describe el número de cada periodo que en conjunto forman el plazo que se pacto, a través del cual se va a liquidar el crédito.

En la segunda columna, lleva por nombre saldo insoluto, que como se puede observar, la primera casilla, describe la cantidad que fue otorgada el crédito, que en el ejemplo que se está manejando corresponde a la cantidad de \$80 mil pesos, en otras palabras es el total de la deuda. Para la siguiente celda, aparece el saldo insoluto que corresponde al final del periodo anterior, el cual aparece en la columna 6, y se calcula como el saldo al principio del periodo de la columna 2 menos el capital contenido en el pago de la columna 5, esto es, $\$80,000-\$6,360.366=\$73,639.634$.

De forma análoga, se hace el cálculo de los demás renglones, el saldo insoluto es la cantidad que aparece al principio del periodo que es igual al saldo insoluto al final del periodo anterior. Esto ocurre porque el tiempo que pasa entre el fin de un periodo y el inicio de otro es cero.

En la tercera columna, corresponde al pago, que consiste en la cantidad que se va a estar aportando cada periodo, misma que contiene la cantidad que se destina a los intereses, como la cantidad que se destina a pagar la deuda, y es la que se obtuvo en la ecuación de valor y es igual a $\$10,360.366$. Cabe hacer mención que ésta no va a ser modificada, será la misma en las demás celdas.

Columna cuatro, se describe los intereses contenidos en el pago, cantidad que se obtiene de multiplicar el saldo insoluto al principio del período (columna 2), por la tasa de interés efectiva por período, que en éste ejemplo es la misma para toda la duración del crédito, lo cual implica que también es la misma para todos los periodos. Esto es: $(\$80,000)(0.05)=\$4,000$.

Las demás celdas serán calculadas de la misma forma:

(Saldo Insoluto al Principio del Periodo)(Tasa Interés Efectiva Mensual)=

=Intereses Contenidos en el Pago.

En la columna 5, Capital contenido en el pago, cantidad que se obtiene de restar el pago (columna 3) menos los intereses contenidos en el pago (columna 4), es decir;

$(\$10,360.366)-(\$4,000)=\$6360.366$

Esta es la cantidad, que en verdad se aporta en ésta mensualidad para liquidar la deuda.

Finalmente, en la columna 6, Saldo insoluto al final del periodo, corresponde a la cantidad que falta aún por pagar. Se obtiene de la siguiente operación

Saldo insoluto al principio del período (columna 2) menos el capital contenido en el pago (columna 5), lo que es igual al saldo insoluto al final del periodo, esto es:

$(\$80,000)-(\$6360.366)=\$73,639.634$

De forma análoga, se van a construir las demás filas, sin embargo, es necesario considerar que el saldo insoluto al final del periodo es el mismo que el saldo insoluto que aparecerá al principio del segundo.

Recapitulando, algunos puntos importantes de la tabla de amortización que se acaba de construir, destacan:

• El saldo insoluto al principio del periodo, que corresponde a la columna 2, y el saldo f insoluto al final del periodo (columna 6), van a ir disminuyendo en cada fila, esto ocurre porque cada renglón se representa un periodo, en el que se realiza un pago, y por consiguiente se liquida una parte de la deuda. Ésta es la misma razón, por la que al final de la tabla, el saldo insoluto al final del periodo debe quedar en cero, pues en el último periodo es cuando se liquida por completa la deuda.
• En el ejemplo que se manejó, se pactaron que las mensualidades fueran las mismas, de un pago de $\$10,360.366$ en cada una, sin embargo; no siempre van a ser así, ya que como se ha visto en el tema de las anualidades, hay ocasiones en las que, dependiendo del tipo de éstas, con que se elija trabajar para hacer el pago de algún crédito, van a estar determinados los pagos.
• Los intereses contenidos en el pago, que corresponde a la columna 4, también van a estar disminuyendo, esto ocurre porque conforme se vaya avanzando en las mensualidades, se va a ir disminuyendo la cantidad que aún falte por pagar, y como los intereses son calculados justamente a partir de la cantidad que se deba (saldo insoluto), pues mientras menos se deba, menos intereses se irán pagando.

El pago de $\$10,360.366$, ya contiene la cantidad que se destina a liquidar los intereses, así como, la cantidad que se destina para liquidar la deuda adquirida, esto ocurre porque la forma en que se calcular la anualidad vencida $\prescript{}{10}{\mathbf{A}}_{0.05}$, trae a valor presente cada uno de los pagos, haciendo uso de la expresión: $v_i^1+v_i^2+v_i^3+…+v_i^n$, la cual garantiza que los intereses se están siendo calculados del saldo insoluto.

En la práctica, es frecuente encontrar operaciones de crédito que otorgan éste, a partir de dar cierto enganche, el cual representa un porcentaje del valor total del bien que se está adquiriendo, algunos ejemplos de ésta situación se dan cuando se pretende adquirir un automóvil, algún terreno, electrodomésticos, etc.

En este contexto, lo que regularmente se hace para construir la tabla de amortización es agregar una fila o renglón, el cual jugará el papel de periodo cero de la tabla, en el que quedará registrado el pago de dicho enganche, y como se paga al inicio de la operación, se considera que no ha transcurrido nada de tiempo, de allí su nombre. Es importante señalar que como no ha transcurrido tiempo, entonces no hay intereses que se hayan generado, lo que se interpreta el monto del enganche es directo a liquidar ése porcentaje de la deuda adquirida.

En estos casos lo que se hace es, que el saldo insoluto al principio del periodo cero, se a igual al valor total del bien que se pretende comprar, y el pago que realizan que corresponde al enganche es 100% el enganche y el saldo insoluto al final del periodo es igual al valor total del bien que se va a adquirir menos el enganche pagado. Luego los siguientes renglones son calculados a partir del saldo que se obtuvo de ésta operación, la cual se convierte en la cantidad real por la que se ha adquirido el crédito.

Ejercicios resueltos

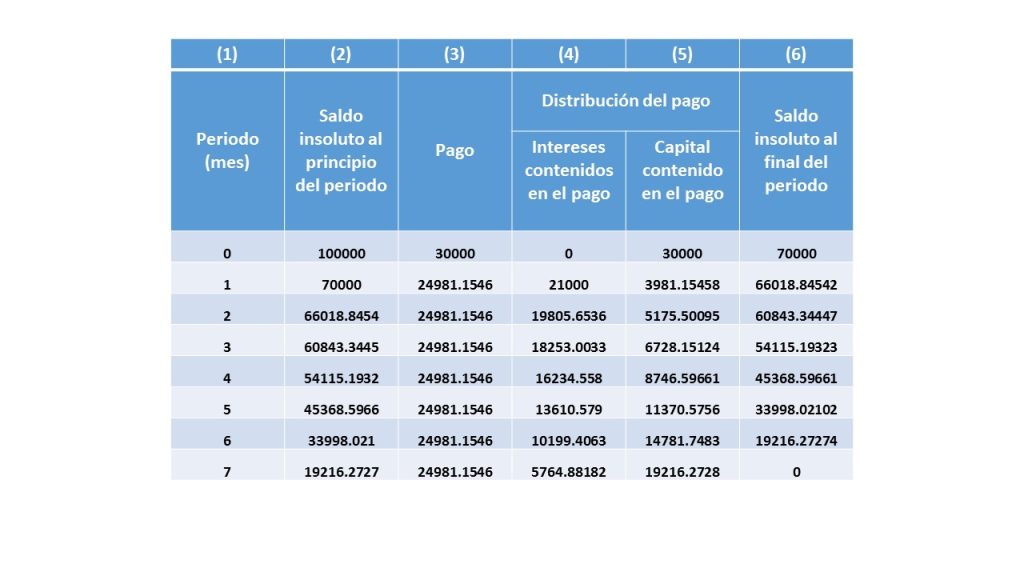
Ejercicio. Una persona desea adquirir un automóvil, con un valor de \$100 mil pesos, pagando un enganche del 30%, y el resto lo quieren pagar en 7 mensualidades con una anualidad vencida de pagos iguales, con una tasa de interés del 15% efectiva anual.

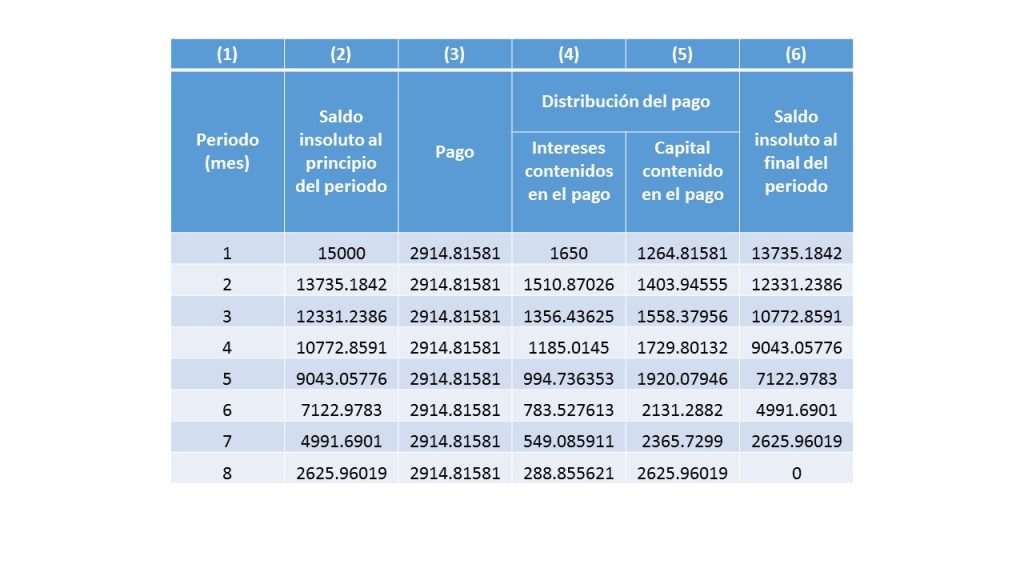
La empresa de estampados del señor Adrián, quiere saber cuánto es la cantidad que deberá tener que pagar, por un crédito de \$15 mil pesos, si la entidad financiera, le esta cobrando una tasa de interés del 11% trimestralmente, durante 2 años

Más adelante…

La tabla de amortización, que se trabajó en ésta sección corresponde a la forma general de construirla, sin embargo, como ya se mencionó puede tener variantes, dependiendo de las condiciones que se pacten entre los involucrados a la hora de firmar el contrato de crédito, como se verá en los siguientes temas.

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente