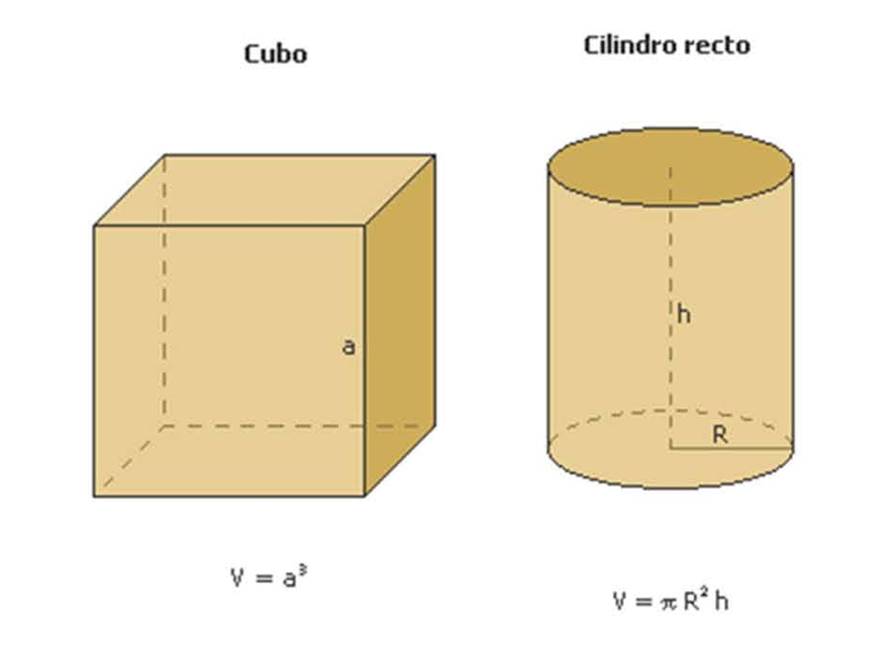
Volumen

Cuando definimos volumen aceptaremos el hecho de que si se trata de
un cubo de lado a entonces $V(cubo)=a^{3}$ y si se trata de un
cilíndro circular recto de radio r y altura h entonces
$V(cil\acute{i}ndro)=\pi r^{2}h$

Ejemplo.- Volumen de un cono de altura a.

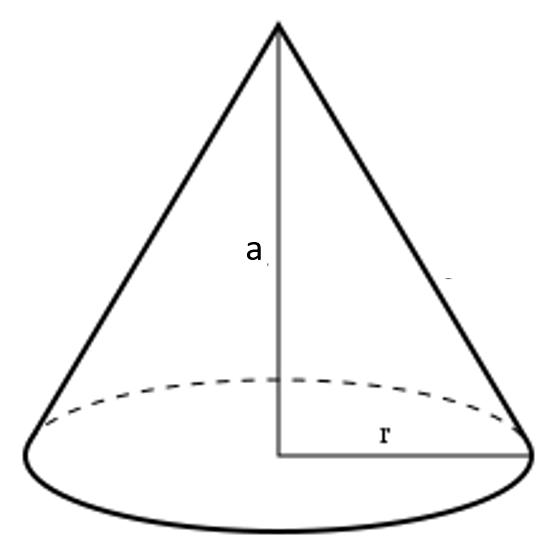
Para esto, dividamos la altura en n partes iguales, cada una de longitud $\displaystyle{\frac{a}{n}}$. Construyamos los n cilindros de altura $\displaystyle{\frac{a}{n}}$ y radio $r_{k}$, k=1,…,n donde $\displaystyle{r_{k}=k\frac{r}{n}}$.

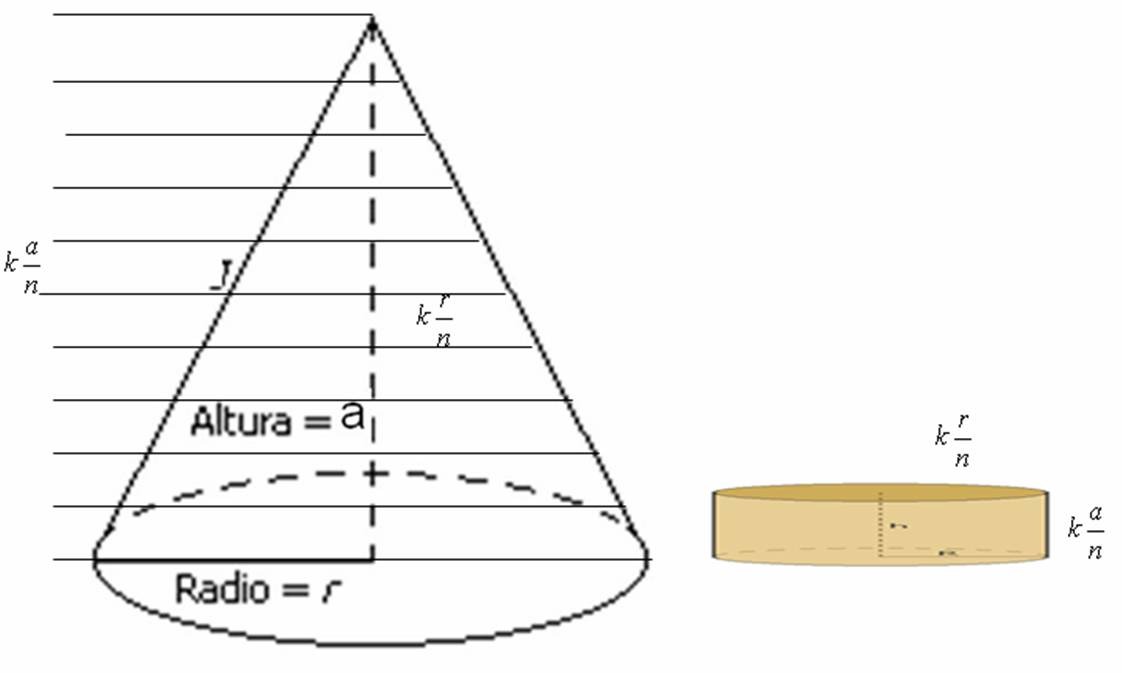
Entonces el volumen del k-ésimo cilindro es
$$V_{k}=\pi r_{k}^{2}a_{k}=\pi \left(k\frac{r}{n}\right)^{2}\left(\frac{a}{n}\right)=\frac{\pi ar^{2}k^{2}}{n^{3}}$$
Por lo tanto el volumen del cono es
$$V\approx \sum_{k=1}^{n}\frac{\pi ar^{2}k^{2}}{n^{3}}=\frac{\pi
ar^{2}}{n^{3}}\sum_{k=1}^{n}k^{2}=\frac{\pi
ar^{2}k^{2}}{n^{3}}\frac{n(n+1)(2n+1)}{6}=\frac{\pi
ar^{2}}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)
$$
En consecuencia
$$V=\lim_{n\rightarrow \infty}\frac{\pi
ar^{2}}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)=\frac{1}{3}\pi a r^{2}$$

Ejemplo. Volumen de una esfera

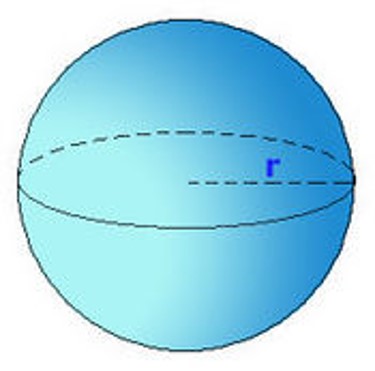
Para esto fijémonos en la mitad de la esfera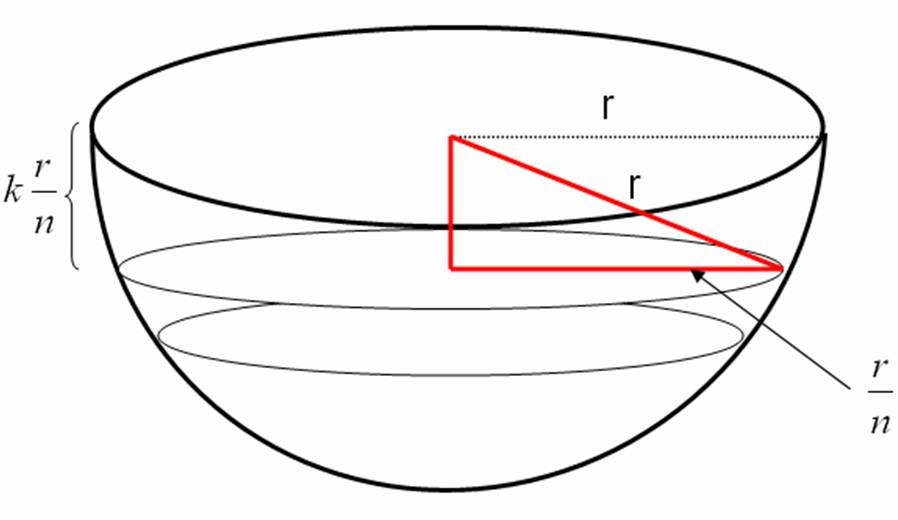

El radio del k-ésimo cilindro es
$$r_{k}=\sqrt{r^{2}-\left(k\frac{r}{n}\right)^{2}}$$
es decir
$$r_{k}^{2}=r^{2}-\left(k\frac{r}{n}\right)^{2}$$
entonces el volumen del k-ésimo cilindro es
$$V=\pi r_{k}^{2}\frac{r}{n}=\pi
\left(r^{2}-\left(k\frac{r}{n}\right)^{2}\right)\frac{r}{n}=\pi
r^{2}\left(1-\frac{k^{2}}{n^{2}}\right)\frac{r}{n}=\pi
r^{3}\left(1-\frac{k^{2}}{n^{2}}\right)\frac{1}{n}$$
Es la mitad de la esfera, por lo que
$$V\approx 2\sum_{k=1}^{n} \pi
r^{3}\left(1-\frac{k^{2}}{n^{2}}\right)\frac{1}{n}=2 \pi
r^{3}\left(\frac{1}{n}\sum_{k=1}^{n}1-\frac{1}{n^{3}}\sum_{k=1}^{n}k^{2}\right)$$
$$=2 \pi r^{3}\left(1-\frac{1}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)\right)
$$
Por lo tanto
$$V=\lim_{n\rightarrow\infty}2 \pi
r^{3}\left(1-\frac{1}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)\right)=\frac{4}{3}\pi r^{3}$$

Ejemplo.- ¿Cual es el volumen del sólido que esta acotado superiormente por un plano e inferiormente por un cilindro?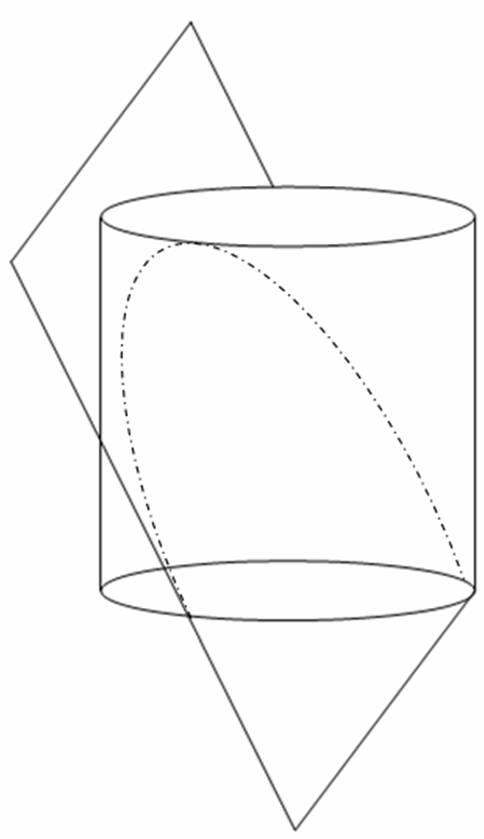

Para resolver esto, dividimos en triángulos rectángulos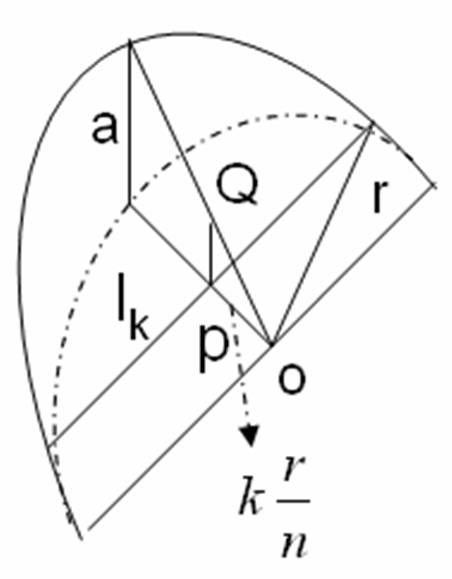

Tenemos que según la figura
$$\left(\frac{l_{k}}{2}\right)^{2}+\left(\frac{kr}{n}\right)^{2}=r^{2}$$
por lo tanto
$$l_{k}=2\sqrt{r^{2}-\left(k\frac{r}{n}\right)^{2}},~~\overline{PQ}=k\frac{a}{n}$$

se tiene entonces que
$$V_{k}=\left(2\sqrt{r^{2}-\left(k\frac{r}{n}\right)^{2}}\right)\left(\frac{ka}{n}\right)\left(\frac{r}{n}\right)$$
$$V\approx
2r^{2}a\sum_{k=1}^{n}\left(\frac{k}{n}\right)\sqrt{1-\left(\frac{k}{n}\right)^{2}}\left(\frac{1}{n}\right)$$

$$V=2r^{2}a\lim_{n\rightarrow
\infty}\sum_{k=1}^{n}\left(\frac{k}{n}\right)\sqrt{1-\left(\frac{k}{n}\right)^{2}}\left(\frac{1}{n}\right)=2r^{2}a\int_{0}^{1}x\sqrt{1-x^{2}}dx=\frac{2r^{2}a}{3}$$