Introducción

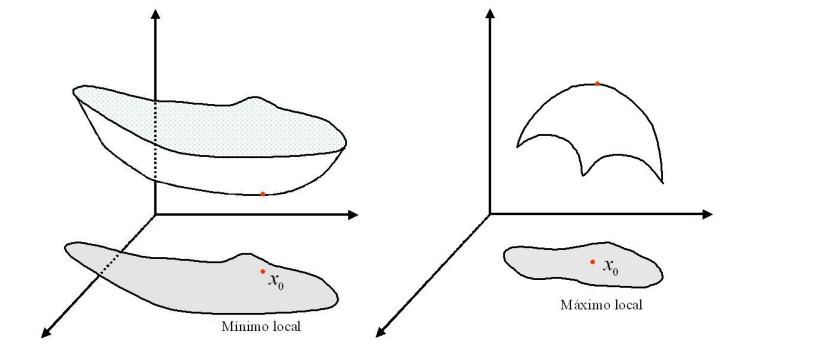
Entre las caracteristicas geometricas básicas de la gráficas de una función estan sus puntos extremos, en los cuales la función alcanza sus valores mayor y menor.

Definición 1. Si $f:u\subset \mathbb{R}^n \rightarrow \mathbb{R}$ es una función escalar, dado un punto $x_0 \in u$ se llama mínimo local de $f$ si existe una vecindad $v$ de $x_0$ tal que $\forall x \in v$, $f(x)> f(x_0)$. De manera análoga, $x_0 \in u$ es un máximo local si existe una vecindad $v$ de $x_0$ tal que $f(x)< f(x_0)$ $\forall \quad x \in v$. El punto $x_0 \in u$ es un extremo local o relativo, si es un mínimo local o máximo local.

Un punto $x_0$ es un punto crítico de $f$ si $Df(x_0)=0$.

Un punto crítico que no es un extremo local se llama punto silla.

Teorema 1. $\textcolor{Red}{\textbf{Criterio de la primera derivada}}$ Si $u \in \mathbb{R}$ es abierto, la función $f:u\subset \mathbb{R}^n \rightarrow \mathbb{R}$ es diferenciable y $x_0 \in u$ es un extremo local entonces $\nabla f(x_0)=0$, esto es $x_0$ es un punto crítico de $f$.

Demostración. Supongamos que $t$ alcanza su máximo local en $x_0$. Entonces para cualquier $h \in \mathbb{R}^n$ la función $g(t)=f(x_0+th)$ tiene un máximo local en $t=0$. Asi, del cálculo de una variable $g'(0)=0$ ya que como $g(0)$ es máximo local, $g(t)\leq g(0)$ para $t > 0$ pequeño
$$\therefore \quad g'(0)=\displaystyle\lim_{t \rightarrow t_0^+}\frac{g(t)-g(0)}{t}=0$$
Análogamente para $t< 0$ pequeño tomamos
$$g'(0)=\displaystyle\lim_{t \rightarrow t_0^-}\frac{g(t)-g(0)}{t}=0$$
Ahora por regla de la cadena $$g'(0)=\frac{\partial f}{\partial x_{1}}(x_{0})h_{1}+\frac{\partial f}{\partial x_{2}}(x_{0})h_{2}+\cdots+\frac{\partial f}{\partial x_{n}}(x_{0})h_{0}=\nabla f(x_{0})\cdot h$$
Así $\nabla f(x_{0})\cdot h=0 \quad \forall \: h$ de modo que $\nabla f(x_{0})=0$. En resumen si $x_0$ es un extremo local, entonces $\displaystyle\frac{\partial f}{\partial x_i}(x_0)=0 \quad \forall~i=1,\ldots,n$. En otras palabras $\nabla f(x_0)=0$. $\square$

Ejemplo. Hallar los máximos y mínimos de la función $f:\mathbb{R}^2 \rightarrow \mathbb{R}$, definida por $$f(x,y)=x^2+y^2-2x-6y+14$$

Solución. Debemos identificar los puntos críticos de $f$ resolviendo $\displaystyle{\frac{\partial f}{\partial x}=0}$, $\displaystyle{\frac{\partial f}{\partial y}=0}$ para $x,y$, $$2x-2=0~~~2y-6=0$$ De modo que el punto crítico es $(1,3)$. Como $$f(x,y)=\left(x^{2}-2x+1\right)+\left(y^{2}-6y+9\right)+4=\left(x-1\right)^{2}+\left(y-3\right)^{2}+4$$ tenemos que $f(x,y)\geq 4$ por lo tanto en $(1,3)$ $f$ alcanza un mínimo relativo.

Ejemplo. Considerar la función $f:\mathbb{R}^2 \rightarrow \mathbb{R}$,
$f(x,y)=4-x^2-y^2$ entonces $\displaystyle{\frac{\partial f}{\partial x}=-2x}$, $\displaystyle{\frac{\partial f}{\partial y}=-2y}$. $f$ solo tiene un punto crítico en el origen, donde el valor de $f$ es 4. Como $$f(x,y)=4-(x^{2}+y^{2})$$
tenemos que $f(x,y)\leq 4$ por lo tanto en $(0,0)$ $f$ alcanza un máximo relativo.

Ejemplo. En el siguiente ejemplo mostramos que no todo punto critico es un valor extremo\Sea $f(x,y)=x^{2}y+y^{2}x$ tenemos que sus puntos criticos son
$$\frac{\partial f}{\partial x}=2xy+y^{2}~\frac{\partial f}{\partial y}=2xy+x^{2}=0$$ por lo tanto $$\left(\begin{matrix}2xy+y^{2}=0\\2xy+x^{2}=0\end{matrix}\right)\Leftrightarrow\left(\begin{matrix}x=y\\x=-y\end{matrix}\right)$$ tomando $x=-y$ tenemos que $$2xy+y^{2}=0~\Rightarrow~-2y^{2}+y^{2}=0~\Rightarrow~y^{2}=0\Rightarrow~y=0~\Rightarrow~x=0$$ tomando $x=y$ tenemos que $$2xy+y^{2}=0~\Rightarrow~2y^{2}+y^{2}=0~\Rightarrow~-3y^{2}=0\Rightarrow~y=0~\Rightarrow~x=0$$ por lo tanto $(0,0)$ es el único punto critico.\Ahora bien para $f(x,y)$ tomamos $x=y$ $$f(x,x)=2x^{3}$$ la cual es ($<0$ si $x<0$) y ($>0$ si $x>0$) por lo tanto el punto critico $(0,0)$ no es ni máximo ni mínimo local de f \Ahora bien para $f(x,y)$ tomamos $x=-y$ $$f(x,-x)=0~\forall x$$
por lo tanto el punto critico $(0,0)$ no es ni máximo ni mínimo local de $f$

Requerimos un criterio que dependa de la segunda derivada para que un punto sea extremo relativo. En el caso particular $n=1$ el criterio es $f»(x)>0$ y $f»(x)<0$ para máximo o mínimo respectivamente para el contexto de varias variables usaremos el hessiano el cual esta definido por

$$Hf(x_0)h=\frac{1}{2}\sum_{i,j=1}^{n}\frac{\partial^2t}{\partial x_i\partial
x_j}(x_0|_{x_ix_j}).$$

Recordando un poco de la expresión de taylor$$f(x,y)=f(x_{0},y_{0})+\left(\frac{\partial f}{\partial x}\right){p}(x-x{0})+\left(\frac{\partial f}{\partial y}\right){p}(y-y{0})+\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial x^{2}}{p}(x-x{0})^{2}+2\frac{\partial^{2}f}{\partial y \partial x}{p}(x-x{0})(y-y_{0})+\frac{\partial^{2}f}{\partial y^{2}}{p}(y-y{0})^{2}\right)}$$

Teorema 2. Sea $B=\left[
\begin{array}{cc}
a & b \\
b & c \
\end{array}
\right]
$ y $H(h)=\frac{1}{2}[h_1,h_2]\left[
\begin{array}{cc}
a & b \\
b & c \
\end{array}
\right]\left(
\begin{array}{c}
h_1 \\
h_2 \
\end{array}
\right)
$ entonces $H(h)$ es definida positiva si y solo si $a>0$ y $ac-b^2>0$.

Demostración. Tenemos $$H(h)=\frac{1}{2}[h_1,h_2]\left[
\begin{array}{cc}
a h_1& bh_2 \\
b h_1& ch_2 \
\end{array}
\right]=\frac{1}{2}(ah_1^2+2bh_1h_2+ch_1^2)$$
si completamos el cuadrado
$$H(h)=\frac{1}{2}a\left(h_1+\frac{b}{a}h_2\right)^2+\frac{1}{2}\left(c-\frac{b^2}{a}\right)h_2^2$$
supongamos que $h$ es definida positiva. Haciendo $h_2=0$ vemos que $a>0$. Haciendo $h_1=-\frac{b}{a}h_2$ $c-\frac{b^2}{a}>0$ ó $ac-b^2>0$ De manera analoga $H(h)$ es definida negativa si y solo si $a<0$ y $ac-b^2>0$. $\square$

Criterio del máximo y del mínimo para funciones de dos variables Sea $f(x,y)$ de clase
$C^3$ en un conjunto abierto $u$ de $\mathbb{R}^2$. Un punto $x_0,y_0$ es un mínimo local (Estricto) de $f$ si se cumple las siguientes tres condiciones:

I) $\frac{\partial f}{\partial x}(x_0,y_0)=\frac{\partial f}{\partial y}(x_0,y_0)$

II) $\frac{\partial^2 f}{\partial x^2}(x_0,y_0)> 0$

III ) $\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right)-\left(\frac{\partial^2 f}{\partial x \partial y}\right)^2> 0$ en $(x_0,y_0)$ (Discriminante)

Si en II) tenemos $<0$ en lugar de $>0$ sin cambiar III) hay un máximo local

Ejemplo. Sea $f:\mathbb{R}^2\rightarrow\mathbb{R}$ la función dada por
$$f(x,y)=2(x-1)^2+3(y-2)^2$$ tenemos entonces que $\frac{\partial f}{\partial x}=4(x-1)$ $\frac{\partial f}{\partial y}=6(y-2)$ por lo tanto $\frac{\partial f}{\partial x}=0$ $\Rightarrow \quad x=1$

$\frac{\partial f}{\partial y}=0$ $\Rightarrow$ $y=2$

por lo tanto $x_0=(1,2)$ es un punto critico

$\displaystyle{\frac{\partial^{2} f}{\partial x^{2}}}=4$, $\displaystyle{\frac{\partial^{2} f}{\partial y^{2}}}=6$, $\displaystyle{\frac{\partial^{2} f}{\partial x\partial y}}=0$, $\displaystyle{\frac{\partial^{2} f}{\partial y\partial x}}=0$

$H(1,2)=\left|\begin{array}{cc}
4 & 0 \\
0 & 6 \
\end{array}
\right|=24> 0 \forall \:(x,y) \in
B_{\epsilon}(1,2)$
podemos decir que $f$ tiene un mínimo relativo en $(1,2)$