Introducción
La derivada direccional en un punto es un concepto del cálculo multivariable que describe cómo cambia una función cuando se mueve desde un punto en una dirección específica.
Diferenciación de funciones $\mathbb{R}^{n}\rightarrow\mathbb{R}$
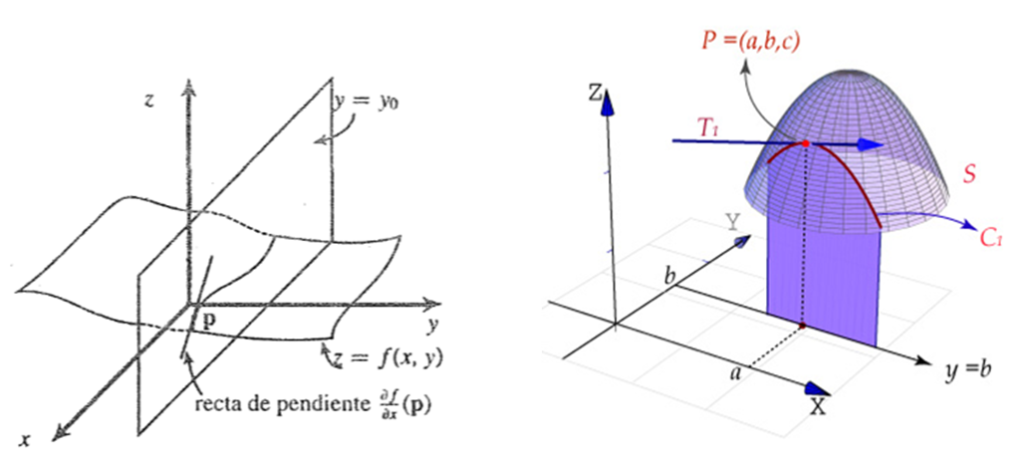
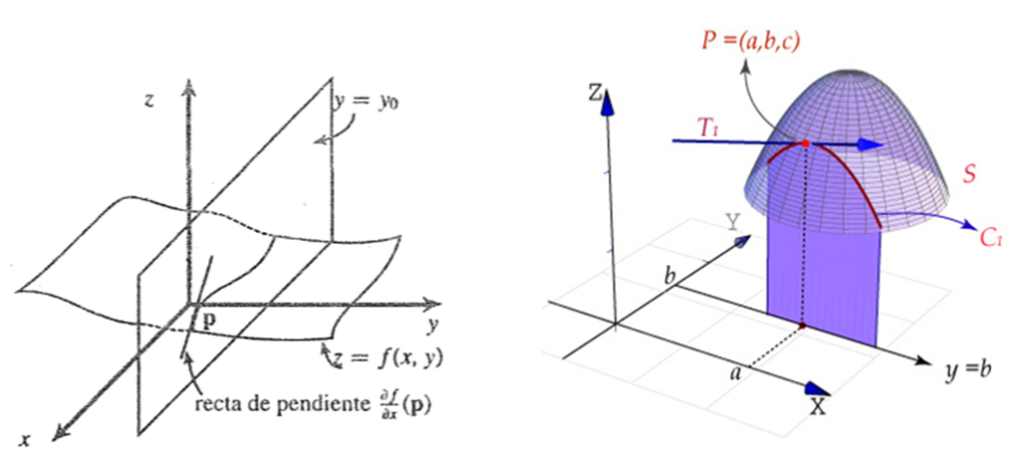
Sea $f:A \subseteq\mathbb{R}^{n}\rightarrow \mathbb{R}$ y $\overline{a}=(a_{1},\ldots,a_{n}) \epsilon {A}$. Se define la derivada pacial $i$-esima en $\overline{a}$ denotada $f_{x}(\overline{a})$, $D_{x}f(\bar{a})$ ó $\displaystyle\frac{\partial f}{\partial x}(\bar{a})$ de la forma $f_{x}=\displaystyle\lim_{h \rightarrow 0}\frac{f(a_{1},\ldots,a_{i}+h,\ldots.a_{n})-f(\bar{a})}{h}=\displaystyle\lim_{h \rightarrow 0}\frac{f(a+he_{i})-f(a)}{h}$ siendo
$\bar{e}_{i}=(0,\ldots,\underset{i-esimo}{1},\ldots,0)$. Si $n=2$ existen 2 derivadas parciales.
Sea $\bar{a}=(x_{0},y_{0})$ un punto del interior del dominio de $f:A \subseteq\mathbb{R}^{2}\rightarrow \mathbb{R}$ las derivas parciales de $f$ en el punto $\bar{a}$ denotada respectivamente por $f_{x}(x_{0},y_{0})$, $f_{y}(x_{0},y_{0})$
son:
$$f_{x}(x_{0},y_{0})=\displaystyle\lim_{h \rightarrow 0}\frac{f(x_{0}+h,y_{0})-f(x_{0},y_{0})}{h}$$
$$f_{y}(x_{0},y_{0})=\displaystyle\lim_{k \rightarrow 0}\frac{f(x_{0},y_{0}+k)-f(x_{0},y_{0})}{k}$$
Sea $f:I\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}y^{3}$
Calcular $f_{x},~f_{y}$
En este caso
$$f_{x}=\lim_{h\rightarrow 0}\frac{f(x+h,y)-f(x,y)}{h}$$
$$=\lim_{h\rightarrow 0}\frac{(x+h)^{2}y^{3}-x^{2}y^{3}}{h}$$
$$=\lim_{h\rightarrow 0}2xy^{3}+hy^{3}=2xy^{3}$$
$$f_{y}=\lim_{h\rightarrow 0}\frac{f(x,y+h)-f(x,y)}{h}$$
$$=\lim_{h\rightarrow 0}\frac{x^{2}(y+h)^{3}-x^{2}y^{3}}{h}$$
$$=\lim_{h\rightarrow 0}3x^{2}y^{2}+hy^{3}$$
$$=3x^{2}y^{2}$$
Ejemplo. Sea
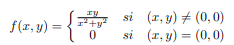
Calculemos $f_{x}(0,0)$
$$f_{x}(0,0)=\lim_{h\rightarrow 0}\frac{f(0+h,0)-f(0,0)}{h}$$
$$=\lim_{h\rightarrow 0}\frac{\frac{h(0)}{h^{2}}}{h}$$
$$=\lim_{h\rightarrow 0}\frac{0}{h^{3}}=0$$
$$f_{y}(0,0)=\lim_{h\rightarrow 0}\frac{f(0,0+h)-f(0,0)}{h}$$
$$=\lim_{h\rightarrow 0}\frac{\frac{(0)h}{h^{2}}}{h}$$
$$=\lim_{h\rightarrow 0}\frac{0}{h^{3}}=0$$
En este caso $f_{x}=0=f_{y}$ sin embargo la función no es continua
Derivada Direccional en un punto
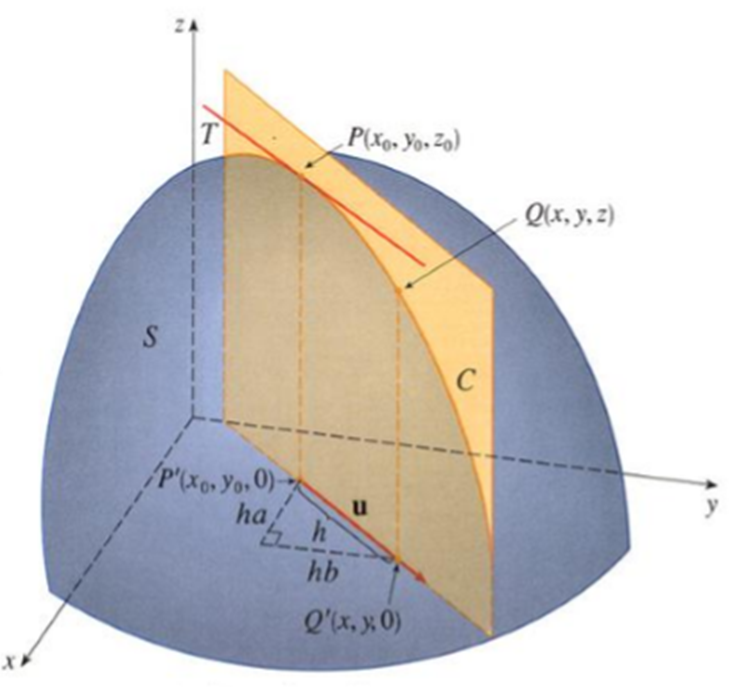
Sea $f:A\subseteq\mathbb{R}^{n}\rightarrow \mathbb{R}$ $x_{0}\in A$. Sea $u\in \mathbb{R}^{n}$ con $|u|=1$ la derivada direcional de $f$ en
la dirección del vector $u$, en el punto $x_{0}$ denotada por $\displaystyle{\frac{\partial f}{\partial u}}(x_{0})$, se define por
$$\displaystyle{\frac{\partial f}{\partial u}}(x_{0})=\displaystyle\lim_{h \rightarrow
0}\frac{f(x_{0}+hu)-f(x_{0})}{h}$$
Ejemplo. Sea $f(x,y)=x^{2}y$ y sea $\displaystyle{u=\left(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}}\right)}$ por lo tanto la derivada direccional en $(x_{0},y_{0})$ es:
$$\lim_{h \rightarrow0}\frac{f\left((x_{0},y_{0})+h\left(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}}\right)\right)-f(x_{0},y_{0})}{h}=\lim_{h \rightarrow0}\frac{\left(x_{0}+\frac{h}{\sqrt{5}}\right)^{2}\left(y_{0}+\frac{2h}{\sqrt{5}}\right)-x_{0}^{2}y_{0}}{h}=$$
$$\lim_{h \rightarrow0}\frac{\left(x_{0}^{2}+\frac{2x_{0}h}{\sqrt{5}}+\frac{h^{2}}{5}\right)\left(y_{0}+\frac{2h}{\sqrt{5}}\right)-x_{0}^{2}y_{0}}{h}=\frac{2x_{0}^{2}}{\sqrt{5}}+\frac{2x_{0}y_{0}}{\sqrt{5}}$$
Notas: 1) La derivada direccional indica la variación de la función en la dirección de $\bar{u}$.
2)Las derivadas parciales son derivadas direccionales respecto a los vectores de la base canonica.
Diferenciabilidad
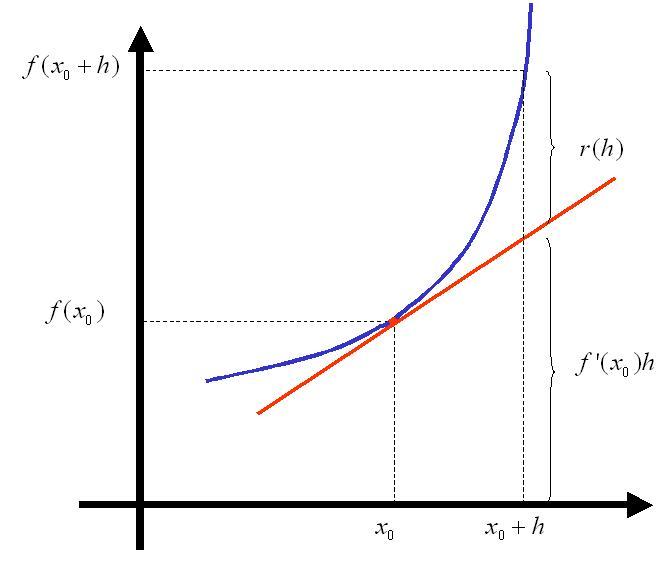
$\textbf{Idea Geometrica}$
$y=f'(x_{0})(x-x_{0})+f(x_{0})$
si $x=x_{0}$
$y=f(x_{0})$
si $x=x_{0}+h$
$y=f'(x_{0})h$
$\therefore$ \qquad $r(h)=f(x_{0}+h)-f(x_{0})-f'(x_{0})h \qquad$ (Diferencial)
donde
$$\frac{r(h)}{h}=\frac{f(x_{0}+h)-f(x_{0})}{h}-f'(x_{0})$$
Debería ocurrir
$$\lim_{h\rightarrow 0}\frac{r(h)}{h}=0$$
Definición. Sea $A\subset\mathbb{R}^{2}$, un abierto, $f:A\rightarrow\mathbb{R}$ y $(x_{0},y_{0})\in A$. Se dice que f es diferenciable en $(x_{0},y_{0})$ si existen constantes $A_{1},~~A_{2}$ tal que
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+A_{1}h_{1}+A_{2}h_{2}+r(h_{1},h_{2})$$donde
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
En la definición anterior si se toma $h=(h_{1},0)$ se tiene
$$f((x_{0},y_{0})+(h_{1},0))=f(x_{0},y_{0})+A_{1}h_{1}+A_{2}(0)+r(h_{1},0)$$donde
$$\lim_{h_{1}\rightarrow0}\frac{f(x_{0}+h_{1},y_{0})-f(x_{0},y_{0})}{h_{1}}-A_{1}=\lim_{h_{1}\rightarrow0}\frac{r(h_{1},0)}{h_{1}}$$
como
$$\lim_{h_{1}\rightarrow0}\frac{r(h_{1},0)}{h_{1}}=0$$se tiene
$$\lim_{h_{1}\rightarrow0}\frac{f(x_{0}+h_{1},y_{0})-f(x_{0},y_{0})}{h_{1}}-A_{1}=0$$
en consecuencia
$$\frac{\partial f}{\partial x}=\lim_{h_{1}\rightarrow0}\frac{f(x_{0}+h_{1},y_{0})-f(x_{0},y_{0})}{h_{1}}=A_{1}$$
En la definición anterior si se toma $h=(0,h_{2})$ se tiene
$$f((x_{0},y_{0})+(0,h_{2}))=f(x_{0},y_{0})+A_{1}(0)+A_{2}h_{2}+r(0,h_{2})$$donde
$$\lim_{h_{2}\rightarrow0}\frac{f(x_{0},y_{0}+h_{2})-f(x_{0},y_{0})}{h_{2}}-A_{2}=\lim_{h_{2}\rightarrow0}\frac{r(0,h_{2})}{h_{2}}$$
como
$$\lim_{h_{2}\rightarrow0}\frac{r(0,h_{2})}{h_{2}}=0$$se tiene
$$\lim_{h_{0}\rightarrow0}\frac{f(x_{0},y_{0}+h_{2})-f(x_{0},y_{0})}{h_{2}}-A_{2}=0$$
en consecuencia
$$\frac{\partial f}{\partial y}=\lim_{h_{2}\rightarrow0}\frac{f(x_{0},y_{0}+h_{2})-f(x_{0},y_{0})}{h_{2}}=A_{2}$$
Definición. Sea $A\subset\mathbb{R}^{2}$, un abierto, $f:A\rightarrow\mathbb{R}$ y $(x_{0},y_{0})\in A$. Se dice que f es diferenciable en $(x_{0},y_{0})$ si existen las derivadas parciales $\displaystyle{\frac{\partial f}{\partial x}(x_{0},y_{0}),~~\frac{\partial f}{\partial y}}(x_{0},y_{0})$ tal que
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$donde
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
Más adelante
Veremos los resultados que caracterizan la derivabilidad de funciones reales en un punto.
Tarea Moral
1.- Si $f(x,y)=x^2y+y^3$, hallar $\displaystyle{\frac{\partial f}{\partial x}}$ y $\displaystyle{\frac{\partial f}{\partial y}}$
2.-Si $z=cosxy+xcosy=f(x,y)$ hallar las derivadas parciales $\displaystyle{\frac{\partial z}{\partial x}}(x_{0}, y_{0})$, $\displaystyle{\frac{\partial z}{\partial y}}(x_{0}, y_{0})$
3.- Evaluar las derivadas parciales $\displaystyle{\dfrac{\partial z }{\partial x}}$, $\displaystyle{\dfrac{\partial z}{\partial y}}$ para las funciones dadas en los puntos indicados.
a) $z=\sqrt{a^2-x^2-y^2}$, $(0,0)$, $(a/2,a/2)$
b) $z=log\sqrt{1+xy}$, $(1,2)$, $(0,0)$
4.-Hallar las derivadas parciales $\dfrac{\partial z}{\partial x}, \dfrac{\partial w}{\partial y}$
$z=e^{\alpha x}cos(bx+y); (2\pi/b,0)$
5.-Hallar $\dfrac{\partial f}{\partial x}$, $\dfrac{\partial f}{\partial y}$
$f(x,y)=(x^2+y^2)log(x^2+y^2)$
Enlaces
La siguiente liga muestra un interactivo en geogebra que nos permite ver lo siguiente para la función $f(x,y)=x^2+y^2$, recuerda que puedes modificarla para insertar la función de tu elección.
Define una superficie $z=f(x,y)$.
Un punto $P$ que se encuentra en la gráfica de la función.
Un vector dirección u.
El plano vertical en esa dirección.
La curva de intersección.
La recta tangente.